基于共同趋势模型的非平稳过程在线监控

林原灵，陈前

（南京航空航天大学机械结构力学及控制国家重点实验室，江苏 南京 210016）

基于共同趋势模型的非平稳过程在线监控

林原灵，陈前

（南京航空航天大学机械结构力学及控制国家重点实验室，江苏 南京 210016）

对于非平稳过程监控，传统的基于数据平稳假设的多元统计过程控制方法是不适用的。针对上述问题，提出了一种基于共同趋势模型的非平稳过程监控方法。共同趋势模型从存在协整关系的非平稳多元变量中辨识出共同因子，将各非平稳过程变量分解成非平稳的共同趋势成分与平稳成分之和的形式。不同于现有的基于协整模型的非平稳过程监控方法，共同趋势模型能够获取各非平稳变量中的平稳成分，消除非平稳共同因子的影响并体现变量间全部的动态均衡关系。将对非平稳过程的监控变为应用共同趋势模型，分解得到各非平稳过程变量中的平稳成分，然后应用传统的多元统计方法，估计平稳成分的统计量及相应的控制限进行监测。石油蒸馏过程监控的实例研究结果表明，所提出的方法比基于协整新息变量的方法具有更可靠的监控效果。

共同趋势模型；过程监控；非平稳过程；协整检验；过程控制；过程系统；系统工程

引 言

随着技术的发展，现代工业过程系统的规模日益扩大，复杂程度不断增加，系统发生故障的风险随之提高。系统发生故障，往往造成人员伤亡和巨大的经济损失。因此，必须对工业过程实时监控以确保能够及时发现并排除故障。随着传感器和计算机技术在过程监控中的广泛应用，海量的过程数据被记录和保存。过程监控数据通常呈现出高维度、结构化分布、维度间强相关性的特征。为了有效分析过程监控中产生的大量数据进而揭示出故障征兆，数据驱动方法被应用于工业过程监控。数据驱动方法无需太多关于过程系统的先验知识，而是通过学习大数据样本来获取数据的结构、分布规律等信息。多元统计过程控制（multivariate statistical process control，MSPC）作为一种数据驱动方法，在工业生产中得到了最广泛的应用[1-2]。MSPC从表征过程系统正常运行的数据中提取出数据的有效信息，应用统计学理论建立统计监控模型，实现工业过程的在线监控。

经典的 MSPC方法中，主元分析（principal component analysis，PCA）、偏最小二乘（partial least square，PLS）、独立成分分析（independent component analysis，ICA）等[3-10]方法得到了广泛应用。进一步，为了提取数据的非线性特征，核主元分析（kernel principal component analysis，KPCA）、核偏最小二乘（kernel partial least square，KPLS）、核独立成分分析（kernel independent component analysis，KICA）等[11-15]方法被发展并被应用于过程监控。但是上述方法对数据的统计特性有假设限制，例如，PCA、PLS假设数据服从平稳高斯分布。ICA则利用了数据的高阶统计量信息，不要求数据服从高斯分布假设，但是常用的 ICA算法，如 Infomax、FastICA等，仍然假设数据分布是平稳的[16]。实际上，受过程系统内部复杂结构的相互作用和外界环境因素的影响，工业大系统的随机过程数据并非总是平稳分布的。对于存在非平稳变量的过程，传统的基于平稳随机过程假设的MSPC方法是不适用的。

对于非平稳过程监控，经典的方法是建立自回归积分移动平均（autoregressive integrated moving average，ARIMA）模型[17]。然而，建立ARIMA模型需对时间序列数据做差分，导致了数据中动态信息的丢失，并使得用已建立的ARIMA模型对新样本做预测成为难题。协整理论[18-20]是近年来计量经济学学者发展的一种非平稳多元时间序列分析方法，已成功在催化裂化过程（FCCU）、石油蒸馏过程等[21-23]工程领域证明了其有效性。协整理论指出，对于存在动态均衡关系的多变量非平稳过程，非平稳变量的某个线性组合是平稳的。协整方法先用协整检验方程求出协整向量，再将非平稳变量在协整向量空间上做投影，得到平稳的协整新息变量。协整理论将非平稳时间序列的长期趋势和短期动态特征相结合，克服了ARIMA模型的不足。但是，现有的基于协整模型的监控方法存在缺陷：新息变量只包含了一组协整关系，对于存在多组协整关系的变量，未能体现变量间的全部动态均衡关系，因而抗干扰性不强。为了增强非平稳过程监控效果，本研究提出了基于共同趋势模型的非平稳过程监控方法。共同趋势模型是在协整理论基础上发展的一种非平稳时间序列模型。Stock等[24]提出了共同趋势表达，证明了存在协整关系的多变量非平稳过程中的各变量可以分解成非平稳的共同趋势成分与平稳成分之和的形式，其中共同趋势成分由称为共同因子的一阶单整过程驱动生成。相较于协整模型，共同趋势模型的最大优点是能够消除非平稳共同因子的影响，提取出各非平稳变量的平稳成分，平稳成分包含了变量间全部的动态均衡关系。对于非平稳过程监控，先用共同趋势模型提取出各非平稳变量的平稳成分，再计算出平稳成分的统计量及其相应的控制限，从而实现非平稳工业过程的在线监控。

1 共同趋势模型

1.1 平稳性检验与协整检验

多元随机过程变量建立共同趋势模型的前提条件是：①过程变量的各分量是同阶单整非平稳的；②变量间存在协整关系。因此，首先要对各变量进行平稳性检验以确保各变量是同阶单整的。对于一个非平稳的时序变量xt，定义xt的一阶差分形式为Δxt≡xt−xt−1，若 Δxt是平稳的，则称 xt是一阶单整的，记为 I(1)。为简单起见，下文讨论的非平稳变量均是一阶单整的。目前较为通用的平稳性检验方法是 Augmented Dickey-Fuller（ADF）单位根检验[25]，其核心思想是非平稳变量可以表示为包含单位根的自回归模型的形式。ADF检验的检验方程为：

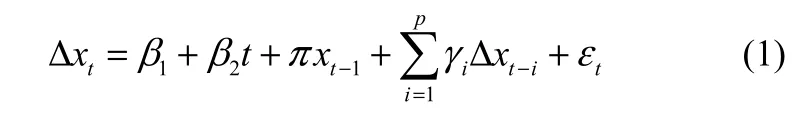
式中，p为滞后阶数，通常根据最小化Akaike信息准则（Akaike information criterion，AIC）[26]的原则确定；Δxt为xt的差分；β1为均值；β2t为线性趋势；π、γ1、…、γp为常系数；εt为残差。使用最小二乘法对式(1)进行参数估计，通过比较式(1)中的系数π的t统计量与给定显著性水平下的t分布临界值，从而判断序列xt是否平稳。具体的检验流程可以参阅文献[25]。

在确定变量的平稳性后，接下来需要使用协整检验来判定非平稳的变量间是否存在协整关系并估计出协整向量。记Xt为n×1的多元非平稳变量，如果存在一个非零向量β∈Rn，使得ξt=βTXt是平稳的，则称Xt是协整的，β是协整向量，ξt是新息变量。对于一阶单整多变量的协整检验，通常使用对参数进行极大似然估计的Johansen检验[27-28]方法。建立关于 n维一阶单整向量 Xt的向量自回归（vector autoregression，VAR）模型：

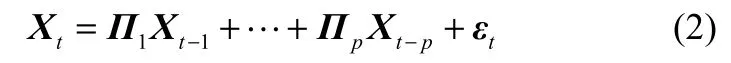
式中，Π1、…、Πp均为n×n的自回归系数矩阵；残差εt为独立同分布的零均值协方差平稳过程；滞后阶数p通常根据最小化AIC的原则确定：

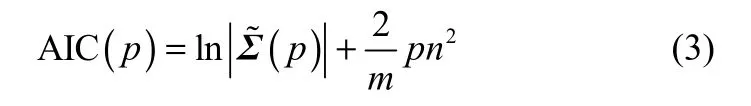
式(2)可以改写成关于 Xt的向量误差修正模型（vector error correction model，VECM）的形式：

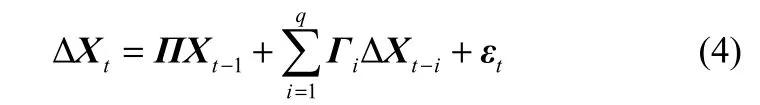
Johansen检验使用最小二乘法对以下两式进行参数估计：

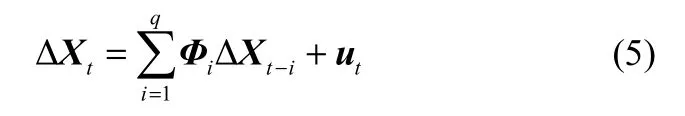
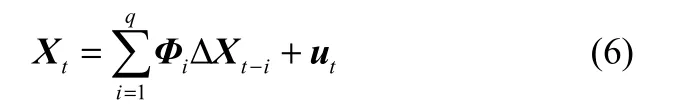
得到式(5)和式(6)中残差 ut的估计，分别记为和，满足关系：

最后，求解式(9)的特征方程

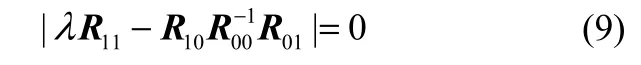
对求解得到的特征值按照 λ1≥λ2≥…≥λn的顺序排列。Johansen检验根据特征值的迹统计量和最大特征值统计量检验协整关系的个数，检验假设为：

对应的迹统计量和最大特征值统计量的定义分别如式(10)和式(11)所示：

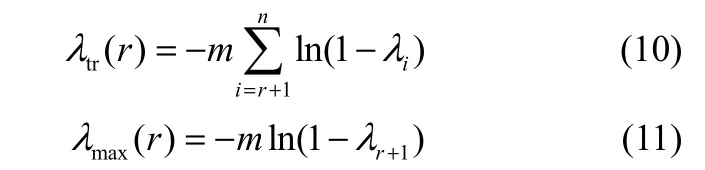
其中，m是样本数，λi是解式(9)得到的第i个最大特征值。Johansen检验从不存在协整关系的零假设H0(r=0)开始，如果拒绝零假设，则逐次增加零假设中的协整关系个数，检验至多存在一个协整关系的零假设H0(r=1)。重复上述步骤，直到接受零假设停止检验，此时零假设中r的值即变量间的协整关系个数。式(9)的前r个最大特征值λ1,…,λr所对应的特征向量构成了协整系数矩阵β的列向量。进一步，调整系数矩阵α的最大似然估计表达式为：

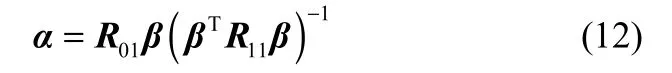
具体的检验流程及相关公式的推导可以参阅文献[27-28]。

1.2 共同趋势表达

Stock等[24]提出了共同趋势表达（common trends representation）方程。共同趋势表达是共同趋势模型的理论基础，它表明：存在协整关系的一阶单整非平稳多元变量的各个分量可以分解为一阶单整的共同趋势成分和平稳成分之和的形式，其中共同趋势成分由若干个被称作共同因子的一阶单整过程驱动生成。对于多元变量Xt∈Rn，Xt的每个分量是一阶单整的，则相应的 VAR模型的特征多项式Π(z)可以变形为：

即多项式分解成单位根部分和不含单位根的平稳部分。因此形如式(4)的误差修正模型可以改写为：

式(14)中，L是滞后算子，C(L)=[Π*(L)]−1，，C(0)是n×n的单位矩阵。式(14)即形为式(4)的误差修正模型对应的向量移动平均（vector moving average, VMA）的表达形式。令C(L)= C(1)+(1−L)C*(L)，代入式(14)做积分，不考虑Xt中的确定性成分，得到如下的关于Xt的向量移动平均表达式：

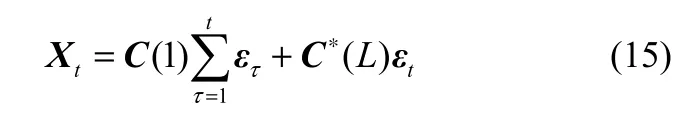
如果变量Xt间存在r个协整关系，记β为n×r的协整矩阵，β的每一列为Xt的一个协整向量，则βTXt是平稳的，因此βTC(1)=0，且C(1)的秩为n−r，即存在n×(n−r)的列满秩矩阵H1、H2，使得C(1)可以分解为C(1)=H1H2T的形式。因此，式(15)可以改写成如下的形式：

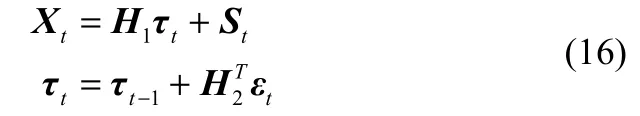
式(16)中，H1τt称为Xt的共同随机趋势成分，简称共同趋势成分，τt是一个(n−r)×1的向量，其各个分量可被视作随机游走过程，因而Xt各变量的共同趋势成分是一阶单整的非平稳过程，St=C*(L)εt称为Xt的平稳成分，其各变量是协方差平稳的。式(16)被称为Stock-Watson共同趋势表达。共同趋势表达方程表明：对于存在r个协整关系的n维一阶单整变量，其各变量可以分解成非平稳的共同趋势成分和平稳成分之和的形式，其中共同趋势成分由n−r个一阶单整过程驱动生成。

由式(16)可以得到共同趋势模型的一般形式：

式(17)中，ft被称为共同因子，其各个分量是一阶单整的，是Xt非平稳并且存在协整关系的原因；是平稳成分，其各个分量是二阶平稳的。

1.3 Gonzalo-Granger分解

共同趋势表达证明了存在协整关系的多元一阶单整变量存在共同因子，但并没有直接提供辨识出变量的共同趋势成分和平稳成分的方法。为了有效地识别出共同趋势成分和平稳成分，必须对共同趋势成分或平稳成分的性质施加一定的限制条件。基于不同的限制条件，不同的共同趋势模型[29-30]被提出。目前，Gonzalo-Granger分解[30]是应用最广泛的共同趋势模型之一。

Gonzalo等[30]提出，对于式(17)，使用以下两个限制条件可以辨识出共同因子ft：①ft是Xt的线性组合；②式(17)可以被看成永久-瞬态（permanent-transitory, P-T）分解的形式，Aft和分别构成了Xt的永久成分和瞬态成分。

对于各变量均是一阶单整的 n维非平稳变量Xt，Xt的各变量间存在r个协整关系，定义α, β∈Rn×r分别为调整系数矩阵和协整系数矩阵，则形如式(4)的误差修正模型可以改写成：

由条件①可知，共同因子ft可以表示为：

其中B是一个(n−r)×n的变换矩阵。将式(19)代入式(17)，则=(I−AB)Xt。由于是平稳的，可以表示成=A1βTXt的形式。

根据条件②，Gonzalo等[30]定义了一阶单整序列Xt的P-T分解形式：①Xt=Pt+Tt，其中Pt是永久成分，Tt是瞬态成分；②Pt的各个分量是一阶单整的，Tt的各分量是平稳的；③令

为(ΔPt,Tt)的自回归表达，并且uPt和uTt是不相关的，则

其中Et表示对过去历史的条件期望。该限制条件表明只有永久成分Pt的新息项uPt对Xt有长期影响。结合式(18)，由于ft为Xt的线性组合，要使得对Xt没有长期影响，即ΔXt的线性组合不包含 βTXt−1的成分，则唯一的线性组合为，其中α⊥是α的正交补矩阵。对矩阵(α⊥, β)T求逆，得到关于 Xt的P-T分解表达式：

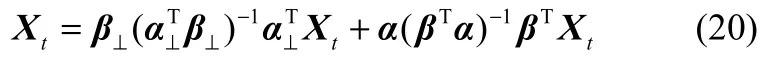
式(20)中，等号右边第1项表示Xt的永久成分，即共同趋势模型中的共同趋势成分，等式右边第2项表示 Xt的瞬态成分，即共同趋势模型中的平稳成分。式(20)即Gonzalo-Granger分解共同趋势模型。

在上述共同趋势模型研究工作的基础上，Escribano等[31]进一步系统地论证了协整模型、Stock-Watson共同趋势表达和Gonzalo-Granger分解之间的等价关系，表明①共同因子是非平稳变量间存在协整关系的原因，②平稳成分体现了变量间的全部动态均衡关系。相关结论和具体证明可以参阅文献[31]。

1.4 数值仿真

为了验证共同趋势模型的有效性，应用Gonzalo-Granger分解来辨识仿真生成的多元一阶单整过程数据的平稳成分。根据共同趋势模型理论，共同趋势成分是一阶单整的，其2阶矩是随时间变化的，而平稳成分是协方差平稳的，其2阶矩是时不变的，因此可以通过比较平稳成分各分量的实际标准差和由共同趋势模型辨识出的平稳成分各分量的标准差来衡量共同趋势模型的分解效果。

仿真数据为包含 3个变量的多变量非平稳过程，每个变量均受到同一个随机游走过程影响。该过程如下：

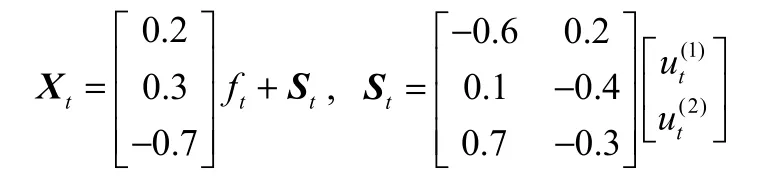
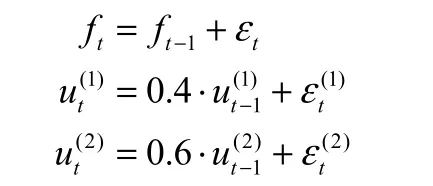
其中εt,,均服从均值为0，标准差为0.5的正态分布， ft是随机游走过程，和均为平稳的AR(1)过程。

由于仿真数据的随机性，为了保证结果的可靠性，仿真数据的样本长度为5000，仿真10000次取平均值。每次仿真时，先对Xt进行Johansen检验，估计出协整系数矩阵β和调整系数矩阵α，再将β和α代入Gonzalo-Granger分解的表达式(20)，得到各变量的共同趋势成分和平稳成分。

表1 仿真数据各变量的平稳成分的标准差Table 1 Standard derivations of simulated stationary components

由表1可知，仿真实验中，Gonzalo-Granger分解辨识出的各变量平稳成分的标准差非常接近实际值，说明该模型能够有效地识别出平稳成分。因此，选择使用 Gonzalo-Granger分解模型用于非平稳过程监控。

2 基于共同趋势模型的非平稳过程在线监控方法

根据共同趋势模型的相关理论，存在协整关系的多元非平稳过程变量可以分解成非平稳的共同趋势成分和平稳成分，其中平稳成分体现了变量间全部的动态均衡关系。由于平稳成分是协方差平稳的，因此可以将平稳成分提取出来，消除非平稳共同趋势成分的影响，应用经典的多元统计方法对其进行监控。对于存在协整关系的非平稳工业过程，先使用共同趋势模型提取出正常工况下各非平稳过程变量的平稳成分。当工业过程系统发生故障，变量间的动态均衡关系被破坏，此时，依照正常模型从故障数据提取出的“平稳成分”不再服从正常工况时平稳成分的统计规律。基于上述思想，提出了基于共同趋势模型的非平稳过程监控方法。与文献[22]中基于协整新息变量的监控方法的区别在于，本方法是对非平稳变量的平稳成分进行监控，而后者是对非平稳变量协整模型的新息变量进行监控，但是新息变量不能全面地反映变量间的动态均衡关系。相似之处在于新息变量与平稳成分都是二阶平稳的，两者可以使用相同的统计指标。本文使用的监控指标是Hotelling的T2统计量[32]，与文献[22]相同。

2.1 监控统计量

对于多元变量监控，Hotelling的T2统计量是最常用的监控指标之一。对于数据集 X∈Rn×m，其中n表示变量维度，m表示样本个数，为了消除变量尺度不同带来的影响，先对X做归一化处理，即每个样本分别减去变量的样本均值再除以相应的样本标准差。记Z∈Rn×m为标准化的数据集，计算Z的样本协方差矩阵：C=ZZT/(m−1)，接着对协方差矩阵进行特征值分解，并按照特征值的大小进行降序排列：C=PΛPT，其中Λ表示k个最大特征值构成的对角矩阵，即Λ=diag(λ1, λ2,…,λk)，P为由k个特征值对应的特征向量构成的载荷矩阵。在确定k的大小时，通常采用累积方差贡献率方法。累积贡献率定义为，通常取累积方差贡献率不小于 85%即认为包含了原始数据足够多的信息。对于每个样本z，按下式计算Hotelling的T2统计量：

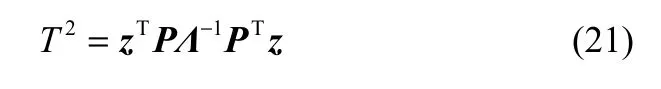
在数据服从协方差平稳分布的假设下，Hotelling的T2统计量的控制限由F分布估计：

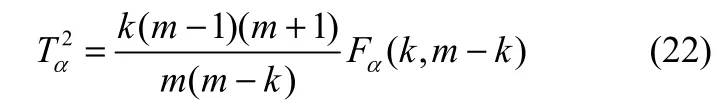
式(22)中，Fα(k, m−k)表示在置信水平α上自由度为k和(m−k)的F分布。

2.2 监控流程

基于共同趋势模型的非平稳过程监控流程如图1所示。

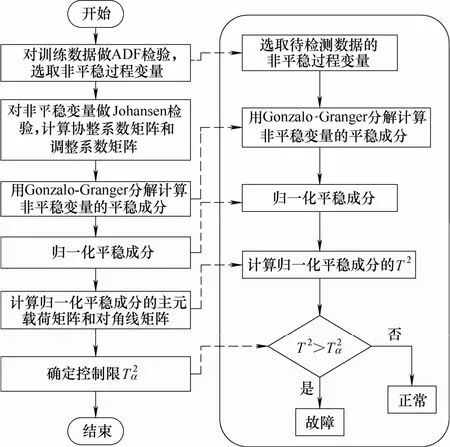
图1 基于共同趋势模型的非平稳过程监测方法Fig.1 Non-stationary process monitoring using common trends models

2.2.1 建立正常工况下的模型

（1）对正常数据集样本的各个变量及其一阶差分变量进行 ADF单位根检验，选取出一阶单整变量Xt=(x1t, x2t, …, xnt)T，将它们作为建模变量。

（2）由式(3)的AIC准则确定Xt的VAR模型的滞后阶数，再依据式(5)～式(12)及相应流程，对Xt进行Johansen检验，确定Xt各变量间的协整关系个数，并计算出协整系数矩阵β和调整系数矩阵α。

（3）根据 Gonzalo-Granger分解表达式(20)，得到 Xt中的平稳成分 St=WXt，其中投影矩阵W=α(βTα)−1βT。

（4）对平稳成分St进行归一化处理，使得归一化后的平稳成分的各分量为零均值和单位方差。

（5）选择合适的方差累积贡献率，计算归一化的平稳成分的载荷矩阵P和对角线矩阵Λ，并由式(22)计算出监控指标Hotelling的T2统计量的控制限。

2.2.2 在线监控

（1）获取新的实时监控数据，根据建模阶段步骤(1)的结果选取出数据中的非平稳过程变量xt。

（2）根据建模阶段步骤(3)获得的投影矩阵求得xt中的平稳成分st=Wxt。

（3）用建模阶段步骤(4)得到的均值和方差对平稳成分st进行归一化处理。

（4）将建模阶段步骤(5)得到的载荷矩阵P和对角线矩阵Λ代入式(21)，计算出归一化平稳成分的Hotelling的T2统计量。

（5）监控Hotelling的T2统计量是否超限。

3 案例研究

3.1 石油蒸馏过程

为了验证本文提出的监控方法的有效性，将该方法应用于某个非平稳的石油蒸馏过程的在线监控。该蒸馏过程用于精馏烃的混合物，出于产品质量和安全因素考虑，共有16个过程变量被监测。关于该过程的详细信息可以参阅文献[22]。该蒸馏过程的工艺流程图如图2所示。

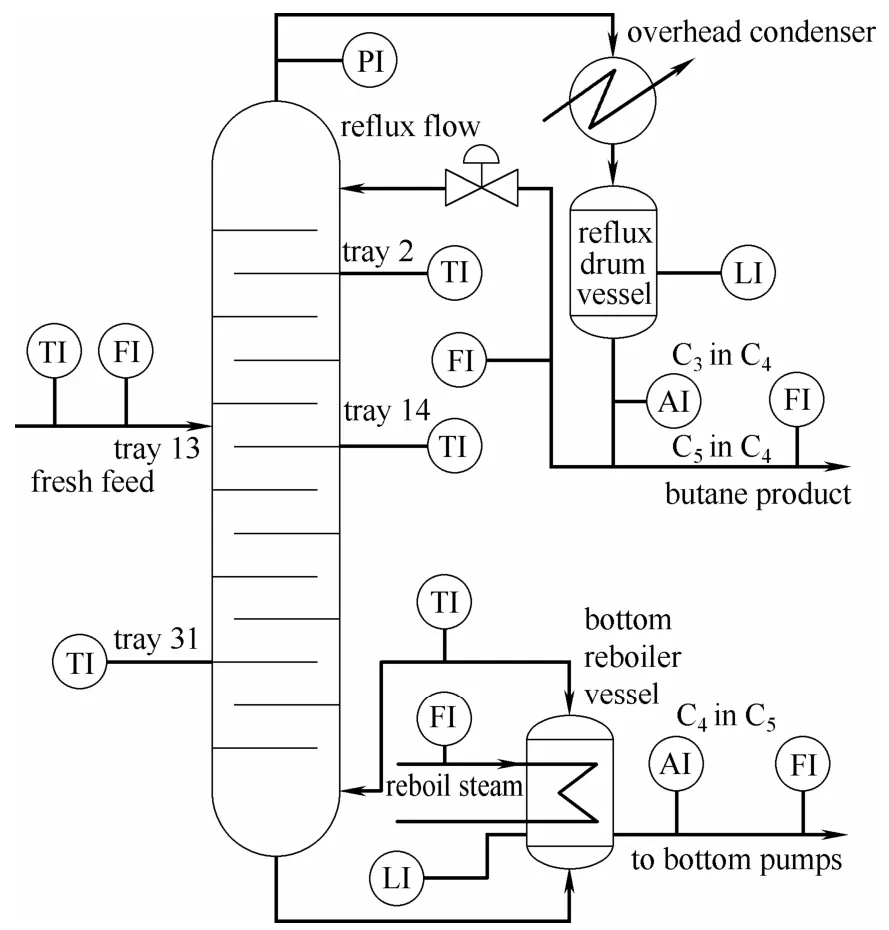
图2 石油蒸馏过程的工艺流程Fig.2 Process flow sheet of distillation process

本文监控的故障是新鲜原料的异常流动，与文献[22]相同。在该过程中，蒸馏塔顶部和底部的产品浓度不受反馈控制，而新鲜原料的流速一直在变化。因此，原料或原料成分的任何异常减少或增加都会导致产品浓度发生变化，降低产品质量。因此必须及时监测到新鲜原料流动异常变化的发生。

样本数据的采样间隔是 30 s，每个样本由 16个过程变量组成。正常数据集包含8000个样本，作为训练集用来建立监控模型。故障数据集包含大约4700个样本，用来验证本文提出方法的有效性。

3.2 监控模型的建立

首先对正常数据集的16个过程变量按式(1)的检验方程进行 ADF检验以确定变量的平稳性，滞后阶数p由AIC准则确定，相应的检验结果见表2。

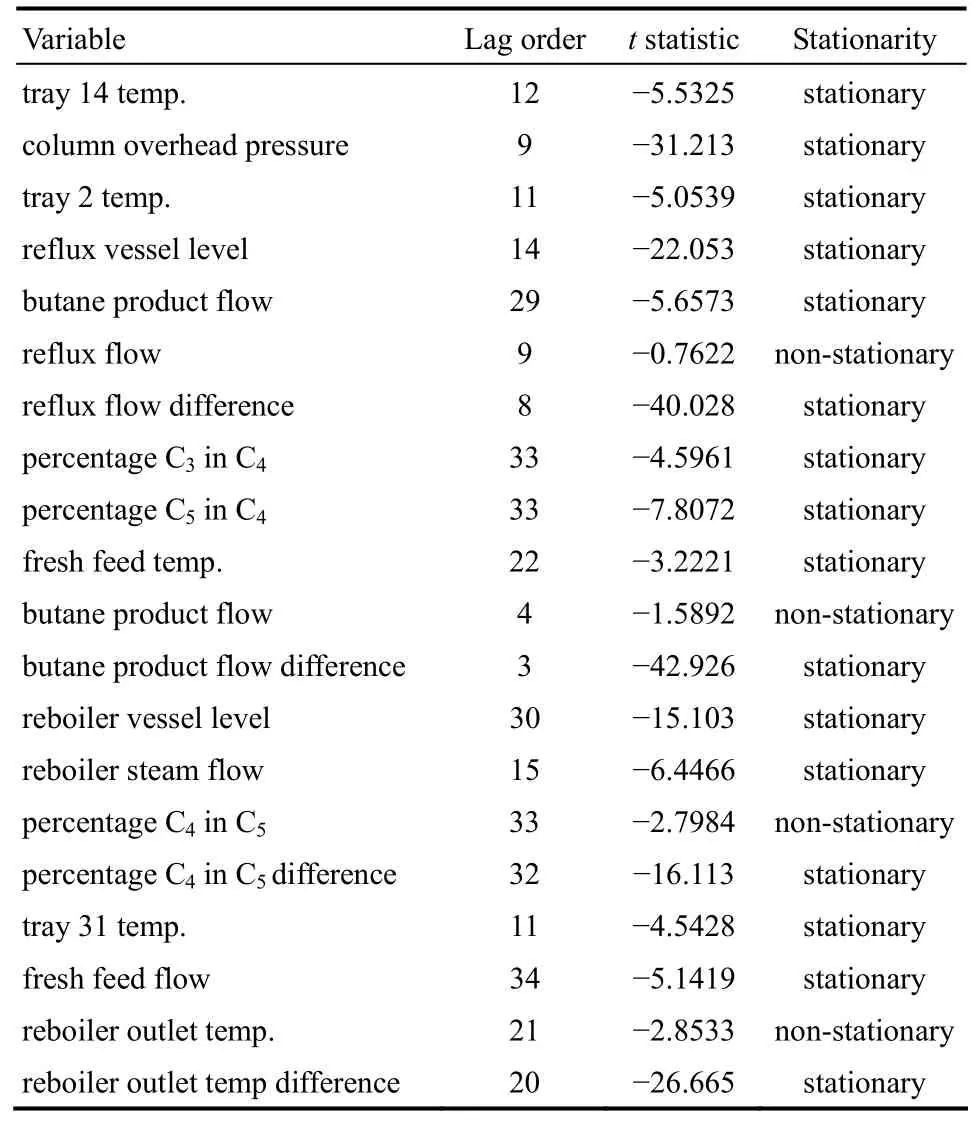
表2 正常数据集过程变量的ADF检验结果Table 2 ADF test results of normal process variables

由ADF检验结果可知，在10%的置信水平上，存在4个一阶单整的非平稳变量，这与文献[22]给出的变量平稳性检验结果一致。接着，对这4个非平稳变量进行Johansen检验，以确定变量间存在的协整关系个数，并估计出协整系数矩阵和调整系数矩阵。对上述非平稳变量建立形如式(2)的VAR模型，由式(3)的AIC准则确定其滞后阶数为13，不同滞后阶数对应的AIC见图3。Johansen迹检验和最大特征值检验的结果分别见表3和表4。

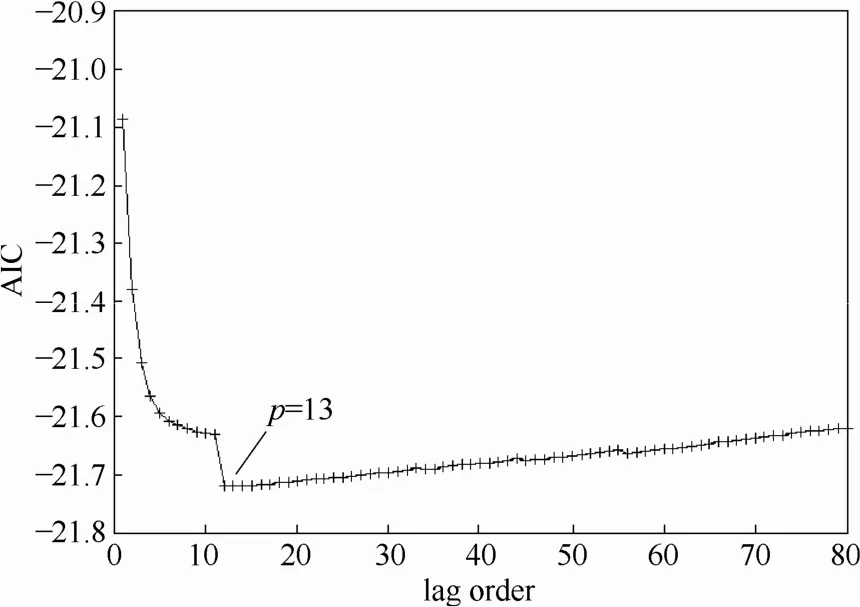
图3 由AIC确定的VAR模型的最佳滞后阶数Fig.3 Optimal VAR lag order determined by AIC

Johansen检验的结果说明，非平稳变量间存在2个协整关系。在按照式(5)～式(12)计算出相应的协整系数矩阵β和调整系数矩阵α之后，根据式(20)的Gonzalo-Granger分解，提取出各个非平稳变量的平稳成分St和共同趋势成分Nt。为了验证提取出的共同趋势成分和平稳成分的平稳性，对St和Nt的各分量进行ADF检验。St各分量的检验结果见表5，Nt各分量的检验结果见表6。检验结果显示，St的各个分量均是平稳的，Nt的各个分量均是一阶单整的，表明共同趋势模型用于非平稳工业过程数据建模是有效的。

表3 Johansen迹检验结果Table 3 Johansen trace test results

表4 Johansen最大特征值检验结果Table 4 Johansen max-eigenvalue test results

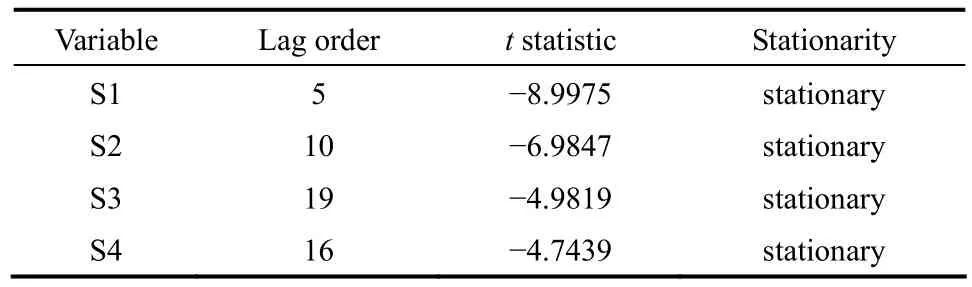
表5 平稳成分的ADF检验结果Table 5 ADF test results of stationary components

接着对从非平稳过程中提取出的平稳成分做归一化处理。计算归一化后的平稳成分的载荷矩阵P和对角线矩阵Λ，由于累积方差贡献率的选取应当不小于85%，因此相应的k值选取为2。再根据式(22)计算出监控指标的控制限，控制限的置信水平为 99%，与文献[22]一致。至此，正常工况下基于共同趋势模型的非平稳过程监控模型被建立。

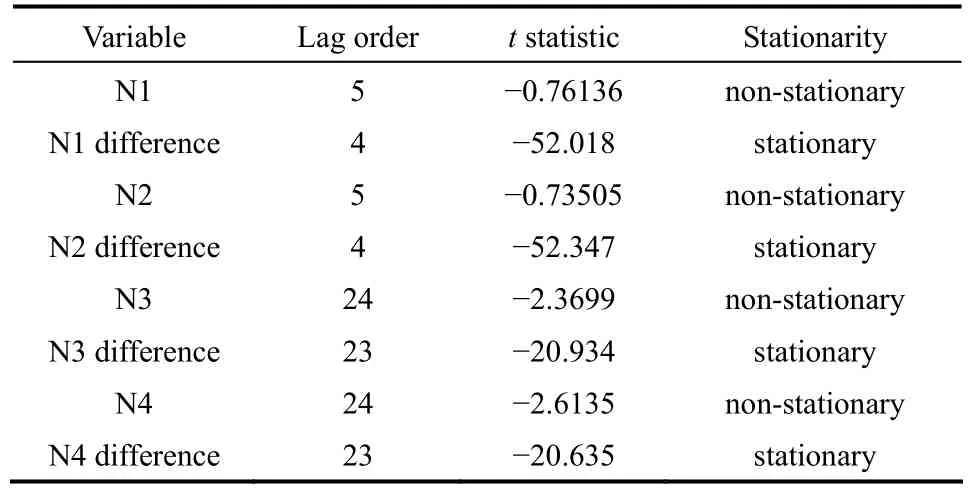
表6 共同趋势成分的ADF检验结果Table 6 ADF test results of common trends components

3.3 故障监控分析与讨论

故障数据表示的是在第1800和第2900个样本点处发生了两次新鲜原料减少。在第1次原料减少发生后，设备操作人员注意到了此次异常的发生，通过降低回流流速抵消了此次异常的影响。但是，当第2次原料减少发生后，设备操作人员未能及时注意到此次异常的发生，直到在大约第4500个样本点处，此时丁烷产品中的杂质含量有了显著增加，设备操作人员才再一次降低了回流流速，抵消了第2次原料减少造成的影响[22]。

将正常模型的协整系数矩阵β和调整系数矩阵α代入式(20)，提取出故障状态下非平稳过程变量的“平稳成分”。接着将正常模型的载荷矩阵 P和对角线矩阵Λ代入式(21)，计算出从归一化后的“平稳成分”的Hotelling的T2统计量，如图4所示。图4中，实横线表示控制限。分析监控结果，在第1800个样本点处第1次原料减少发生后，监控指标超出了控制限，及时做出了预警，由于设备操作人员降低了回流流量，抵消了这次减少造成的影响，监控指标回落到正常水平。在第2900个样本点处新鲜原料再次减少，这次减少未引起操作人员的注意，但监控指标再次超过了控制限，及时做出了预警，证明了本文提出的监控方法的有效性。

图4 基于共同趋势模型的监测结果Fig.4 Monitoring results for fresh feed drops using common trends model

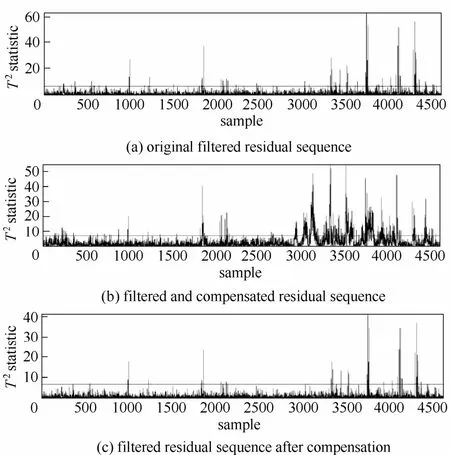
图5 基于文献[22]方法的监测结果Fig.5 Monitoring results for fresh feed drops using methods in Ref.[22]

最后，将本文提出方法的监控结果与文献[22]方法的监控结果进行比较。文献[22]提出了一种基于协整新息变量的非平稳过程监控方法，对非平稳过程变量建立协整模型，估计出一组协整向量，得到新息变量，对新息变量进行逆自回归滤波，得到新息变量的自回归残差。图5展示了文献[22]的监控结果，自上至下依次是原始新息变量自回归残差、新息变量的自回归残差及补偿、新息变量去除补偿后的残差的Hotelling的T2统计量控制图。对于第1800个样本点处的第1次原料减少，文献[22]和本文提出的方法均监测到了此次异常的发生，及时地做出了预警。对于第2900个样本点处的第2次原料减少，虽然文献[22]的3组监测指标均监测到了此次异常的发生，但是只有图5(b)的监测指标及时做出了预警，其他两组监测指标均有明显的滞后性，直到第3400个样本点附近才做出预警，而本文提出的方法则及时地做出了预警。此外，文献[22]的 3组监控指标在抗干扰方面存在不足，3组监控指标在第1000个样本处均做出了明显的误报，在第2200个样本点附近，图5(b)的监控指标也做出了明显的误报[22]，相比之下，本文提出的方法没有出现明显的误报，具有更好的抗干扰性。

4 结 论

针对传统的基于平稳假设的多元统计方法不适用于非平稳过程监控的困境，提出了基于共同趋势模型的非平稳过程监控方法。该方法首先应用共同趋势模型提取出各非平稳变量中的平稳成分，然后再对平稳成分应用Hotelling的T2统计量进行状态监测。与现有的基于协整新息变量的非平稳过程监控方法相比，共同趋势模型可以有效地提取出非平稳变量中的平稳成分，消除非平稳的共同趋势成分的影响，平稳成分包含了反映系统非平稳变量间全部的动态均衡关系的信息。对石油蒸馏过程监控的结果表明，基于共同趋势模型的监控方法好于基于协整新息变量的监控方法。

然而，协整及共同趋势模型的相关理论近年来仍在不断发展。进一步的研究包括：①改进协整系数矩阵的计算方法；②非平稳过程变量与平稳过程变量的联合监控。

[1]陈前. 关于工程大系统的状态监测与故障诊断[J]. 振动、测试与诊断, 2002, 22(3): 163-230. CHEN Q. Condition monitoring and fault diagnosis of large-scale engineering system[J]. Journal of Vibration Measurement and Diagnosis, 2002, 22(3): 163-230.

[2]GE Z, SONG Z, GAO F. Review of recent research on data-based process monitoring [J]. Industrial & Engineering Chemistry Research, 2013, 52(10): 3543-3562.

[3]CHEN Q, WYNNE R J, GOULDING P, et al. The application of principal component analysis and kernel density estimation to enhance process monitoring [J]. Control Engineering Practice, 2000, 8(5): 531-543.

[4]童楚东, 史旭华. 基于互信息的PCA方法及其在过程监测中的应用[J]. 化工学报, 2015, 66(10): 4101-4106. TONG C D, SHI X H. Mutual information based PCA algorithm with application in process monitoring [J]. CIESC Journal, 2015, 66(10): 4101-4106.

[5]KANO M, TANAKA S, HASEBE S, et al. Monitoring independent components for fault detection [J]. AIChE Journal, 2003, 49(4): 969-976.

[6]GE Z, SONG Z. Performance-driven ensemble learning ICA model for improved non-Gaussian process monitoring [J]. Chemometrics and Intelligent Laboratory Systems, 2013, 123: 1-8.

[7]HUANG J, YAN X. Gaussian and non-Gaussian double subspace statistical process monitoring based on principal component analysis and independent component analysis [J]. Industrial & Engineering Chemistry Research, 2015, 54(3): 1015-1027.

[8]衷路生, 何东, 龚锦红, 等. 基于分布式 ICA-PCA模型的工业过程故障监测[J]. 化工学报, 2015, 66(11): 4546-4554. ZHONG L S, HE D, GONG J H, et al. Fault monitoring of industrial process based on distributed ICA-PCA model [J]. CIESC Journal, 2015, 66(11): 4546-4554.

[9]GUNTHER J C, CONNER J S, SEBORG D E. Process monitoring and quality variable prediction utilizing PLS in industrial fed-batch cell culture [J]. Journal of Process Control, 2009, 19(5): 914-921.

[10]韩敏, 张占奎. 基于改进核主成分分析的故障检测与诊断方法[J].化工学报, 2015, 66(6): 2139-2149. HAN M, ZHANG Z K. Fault detection and diagnosis method based on modified kernel principal component analysis [J]. CIESC Journal, 2015, 66(6): 2139-2149.

[11]LEE J M, YOO C K, CHOI S W, et al. Nonlinear process monitoring using kernel principal component analysis [J]. Chemical Engineering Science, 2004, 59(1): 223-234.

[12]LEE J M, QIN S J, LEE I B. Fault detection of non-linear processes using kernel independent component analysis [J]. The Canadian Journal of Chemical Engineering, 2007, 85(4): 526-536.

[13]ZHANG Y. Enhanced statistical analysis of nonlinear processes using KPCA, KICA and SVM [J]. Chemical Engineering Science, 2009, 64(5): 801-811.

[14]胡益, 王丽, 马贺贺, 等. 基于核PLS方法的非线性过程在线监控[J]. 化工学报, 2011, 62(9): 2555-2561. HU Y, WANG L, MA H H, et al. Online nonlinear process monitoring using kernel partial least squares [J]. CIESC Journal, 2011, 62(9): 2555-2561.

[15]GODOY J L, ZUMOFFEN D A, VEGA J R, et al. New contributions to non-linear process monitoring through kernel partial least squares [J]. Chemometrics and Intelligent Laboratory Systems, 2014, 135: 76-89.

[16]COMON P, JUTTEN C. Handbook of Blind Source Separation: Independent Component Analysis and Applications [M]. Academic Press, 2010.

[17]BERTHOUEX P M, BOX G E. Time series models for forecasting wastewater treatment plant performance [J]. Water Research, 1996, 30(8): 1865-1875.

[18]ENGLE R F, GRANGER C W J. Co-integration and error correction: representation, estimation, and testing [J]. Econometrica, 1987, 55(2): 251-276.

[19]PFAFF B. Analysis of Integrated and Cointegrated Time Series with R [M]. Springer Science & Business Media, 2008.

[20]ENDERS W. Applied Econometric Time Series [M]. John Wiley & Sons, 2008.

[21]陈前, 潘昱昱. 协整理论应用于非平稳 FCCU系统的状态监测与故障诊断[J]. 石油学报（石油加工）, 2007, 23(1): 69-76. CHEN Q, PAN Y Y. Application of cointegration testing method to condition monitoring and fault diagnosis of nonstationary FCCU system [J]. Acta Petrolet Sinica (Petroleum Processing Section), 2007, 23(1): 69-76.

[22]CHEN Q, KRUGER U, LEUNG A Y T. Cointegration testing method for monitoring nonstationary processes [J]. Industrial & Engineering Chemistry Research, 2009, 48(7): 3533-3543.

[23]石海忱, 陈前, 林原灵. 协整系数矩阵的非平稳工程系统故障诊断应用研究[J]. 振动与冲击, 2015, 34(1): 146-150. SHI H C, CHEN Q, LIN Y L. Fault diagnosis of non-stationary engineering system using cointegration cofficients matrix [J]. Journal of Vibration and Shock, 2015, 34(1): 146-150.

[24]STOCK J H, WATSON M W. Testing for common trends [J]. Journal of the American statistical Association, 1988, 83(404): 1097-1107.

[25]DICKEY D A, FULLER W A. Distribution of the estimators for autoregressive time series with a unit root [J]. Journal of the American statistical association, 1979, 74(366a): 427-431.

[26]AKAIKE H. A new look at the statistical model identification [J]. IEEE Transactions on Automatic Control, 1974, 19(6): 716-723.

[27]JOHANSEN S, JUSELIUS K. Maximum likelihood estimation and inference on cointegration - with applications to the demand for money [J]. Oxford Bulletin of Economics and statistics, 1990, 52(2): 169-210.

[28]JOHANSEN S. Estimation and hypothesis testing of cointegration vectors in Gaussian vector autoregressive models [J]. Econometrica, 1991, 59(59): 1551-1580.

[29]KASA K. Common stochastic trends in international stock markets [J]. Journal of monetary Economics, 1992, 29(1): 95-124.

[30]GONZALO J, GRANGER C. Estimation of common long-memory components in cointegrated systems [J]. Journal of Business and Economic Statistics, 1995, 13(1): 27-35.

[31]ESCRIBANO A, PEÑA D. Cointegration and common factors [J]. Journal of Time Series Analysis, 1994, 15(6): 577-586.

[32]HOTELLING H. The Generalization of Student's Ratio [M]. New York: Springer, 1992.

Online non-stationary process monitoring by common trends model

LIN Yuanling, CHEN Qian
(State Key Laboratory of Mechanics and Control of Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, Jiangsu, China)

Non-stationary process monitoring based on common trends model was proposed, because conventional multivariate statistical process control methods with stationary data assumption were inapplicable to non-stationary process monitoring. The new common trends model was capable of identifying common factors from co-integrated non-stationary multiple variables and decomposing each non-stationary process variable into summation of a non-stationary common trends component and a stationary counterpart. Contrary to existing non-stationary process monitoring technique from cointegration model, the common trends model captured the stationary component of each non-stationary process variable, eliminated effects of non-stationary common factors and unveiled overall dynamic equilibrium relationships among variables. Hence, non-stationary process monitoring was transformed to an application of common trends model, which involved obtaining stationary component of each process variable, creating estimation for the stationary components by conventional multivariate statistical methods and setting up monitoring on corresponding control limits. A case study of monitoring petroleum distillation process showed that the proposed approach possessed more reliable process monitoring performance than the method of cointegration model.

common trends model; process monitoring; non-stationary process; cointegration testing; process control; process systems; system engineering

Prof. CHEN Qian, q.chen@nuaa.edu.cn

TP 277

：A

：0438—1157（2017）01—0178—10

10.11949/j.issn.0438-1157.20160670

2016-05-16收到初稿，2016-09-25收到修改稿。

联系人：陈前。

：林原灵（1989—），男，博士研究生。

江苏高校优势学科建设工程资助项目。

Received date: 2016-05-16.

Foundation item: supported by the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD).