基于SLP和改进粒子群算法的产品布局优化方法研究

孙 昕， 吉晓民， 王 毅

(1.西安理工大学 机械与精密仪器工程学院,陕西 西安 710048； 2.西安理工大学 艺术与设计学院,陕西 西安 710048)



基于SLP和改进粒子群算法的产品布局优化方法研究

孙 昕1,2， 吉晓民1,2， 王 毅1

(1.西安理工大学 机械与精密仪器工程学院,陕西 西安 710048； 2.西安理工大学 艺术与设计学院,陕西 西安 710048)

产品布局设计要求在一定的功能空间内，各产品满足一定的约束条件且工作效率达到最高。本文从优化角度考虑，将产品布局问题看作是组合优化中的布局问题，在综合考虑产品之间的关系、尺寸、布置方向的基础上，引入工艺专业化布局SLP方法对产品的综合关系进行分析，并以整体厨房产品为例建立数学模型，采用改进粒子群算法进行求解，实现了产品布局优化设计。研究结果表明，采用SLP和改进粒子群算法为解决产品布局优化问题提供了一种有效的途径。该方法可以推广到家具产品布局、陈设用品布局、舱室布局、生产系统布局等方面。

产品; 布局； 优化设计； SLP； 改进粒子群算法

产品布局问题在一定程度上可以看作是组合优化中的布局问题(Placement Problem，PLP)。随着理论研究的深入，很多学者已经研究了大量的求解方法。文献[1]针对船舶居住舱室的布局优化问题采用小生境方法及爬山法；文献[2]针对游艇舱室的布局优化设计提出了基于Pareto前沿的多目标优化方法NSGA-Ⅱ；文献[3]利用伪物理行为以及物体关联的特性确定物体的布局情况，通过粒子群优化算法计算出满足各项约束的参数；文献[4]引入基于人类生活习惯和物理特性的约束，对家居产品进行交互式布局；文献[5]利用层次树对室内各空间家具进行分层优化，并利用粒子群算法进行并行求解。

由于产品布局问题自身评价指标具有多态性和模糊性，决策中往往会融入设计人员的经验、直觉等主观因素，所以很难用精确的数据来评价一个产品布局设计方案的优劣[6]。本文在综合考虑产品之间的邻接需求关系、尺寸、布置方面的基础上，引入工艺专业化布局常用的SLP (System Layout Planning)方法，并采用改进粒子群算法(IPSO)进行求解，为产品布局优化设计提供理论依据。

1 产品布局优化设计

产品布局问题可以通过对数学方法的研究去寻找离散事件的最优编排、分组、次序或筛选等。对于工业产品而言，要求在一定的功能空间内，各产品在布局时满足一定的约束条件和尺度关系，且工作效率达到最高，这几个目标在允许范围内要达到最优，即为最佳布局方案[7]。例如船舶居住舱室中各个家具产品的最优布局可使舱室的有效活动空间利用率最大；飞机驾驶舱中各控制器的最优布局可使飞行员工作时更加舒适、省力。本文以住宅中的整体厨房产品为例，要解决的布局优化问题就是将各产品科学合理地布置在有限的厨房空间内，充分提高工作效率。

1.1 整体厨房产品的功能与分类

现代整体厨房早已突破了传统厨房的概念，厨房中除了满足必须的功能(烹饪、洗涤、储存等)外，还可以进行上网、看电视、洗衣等其它非必须行为，如表1所示。

根据客户需求及行为可将整体厨房分为封闭型厨房和开放型厨房。封闭型厨房又分为K型独立式厨房；UK型家事型厨房；开放型厨房又分为DK型餐事型厨房、LDK型起居式厨房等，如图1所示。

图1 不同类型的整体厨房布局Fig.1 Different kinds of integral kitchen layouts

厨房中必须满足的功能及可能发生的行为烹饪就餐储存洗涤清洁摘菜、清洗、切菜、备餐、烹饪食物(炒，蒸，煮等) 摆桌椅、拿取碗筷、放隔热垫、进餐 餐具、厨具、食物、调味品、杂物 清洁家具、清洗厨具、清洗食物及杂物 整理碗筷、整理剩菜、清洁餐厨空间、处理垃圾厨房中非必须满足的功能及行为洗衣 打电话 上网 看电视 看书、报 小孩做功课

1.2 选择设计变量

整体厨房产品包括橱柜、抽油烟机、燃气灶具、消毒柜、洗碗机、冰箱、微波炉、电烤箱、各式挂件、水盆、抽屉拉篮、垃圾粉碎器及洗衣机、烘干机等，产品的种类及分布根据厨房空间及客户需求的不同而变化。

将厨房原始建筑平面图简化为长l、宽w的矩形平面，各待布物简化为小矩形，设计变量为各待布物的位置参数Xi(i=1,2,…,n)， 即其形心坐标：

式中(xi，yi)为待布物i的形心坐标，n为待布物的数量。

1.3 确定约束条件

1) 由于厨房布局有各种各样的可能性，在实际开发和建设住宅时，厨房的平面类型通常多种多样，建设部相关单位对我国30个示范小区进行了调查，发现有253种厨房平面，面积在2.4～16 m2之间。本文仅以典型厨房平面为例进行布局优化设计。

本文以某住宅厨房为实例，该厨房平面的长度l=5 400 mm，宽度w=3 000 mm，根据客户需求定位为UK型家事型厨房，一般常见的布置形式为一字型、L型或U型，如图2所示。由于篇幅有限，本文仅以L型为例进行布局优化分析。

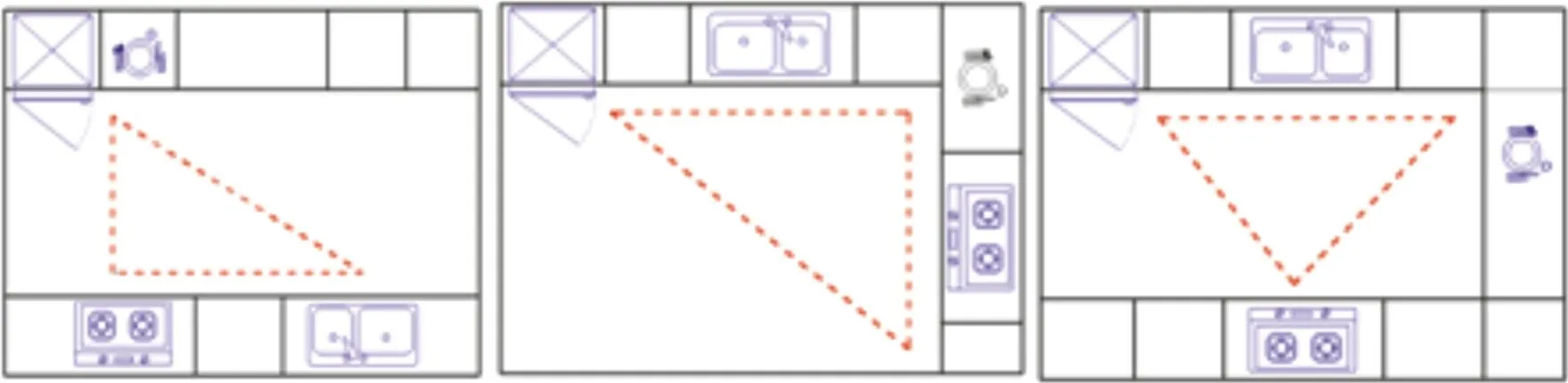
图2 一字型、L型及U型布局Fig.2 One, L and U-shaped layouts

采用L型布局时，文中选取了9个有代表性的产品模块作为待布物体,如表2所示。

表2 整体厨房待布物列表

约束条件为：

当1 500≤xi≤5 100时,yi=2 700

当300≤yi≤2 700时,xi=5 100

2) 各产品之间的不干涉性，即待布物两两不能相交，约束条件为：

(1)

(2)

式中si、qi为待布物i在x、y方向的尺寸，sj、qj为待布物j在x、y方向的尺寸。

3) 待布物不能超出厨房平面图的边界，可用下式表示：

(3)

(4)

1.4 基于SLP的综合强度分析

SLP是工艺专业化布局常用的方法，通过分析各单位之间相互关系的密集程度来对其进行布局[8]。厨房产品由于烹饪行为及水路、电路等关系，有的必须紧邻布置才合理。

本文对SLP方法的构成要素作了简化以进行邻接需求分析，并运用强度系数对要素进行量化表达，用邻接需求强度系数ai,j表示两待布物之间的紧邻关系，ai,j的数值区间为[0,1]，需求强度等级与其所表达的含义如表3所示。

根据调研室内设计行业30位设计师及20位客户代表的综合打分意见，得到邻接需求强度分布矩阵如表4所示。

表3 ai,j等级及含义

表4 ai,j分布矩阵

此外，还要考虑人在厨房各布置物之间活动的频率，如从冰箱拿取食物到备餐台的频率、从调料柜拿取调料到灶台的频率都是比较高的，用bi,j表示人在两布置物之间的流通频率强度， 其数值区间为[0,1],强度等级与含义如表5所示。根据综合打分意见，bi,j分布矩阵如表6所示。

表5 bi,j等级及含义

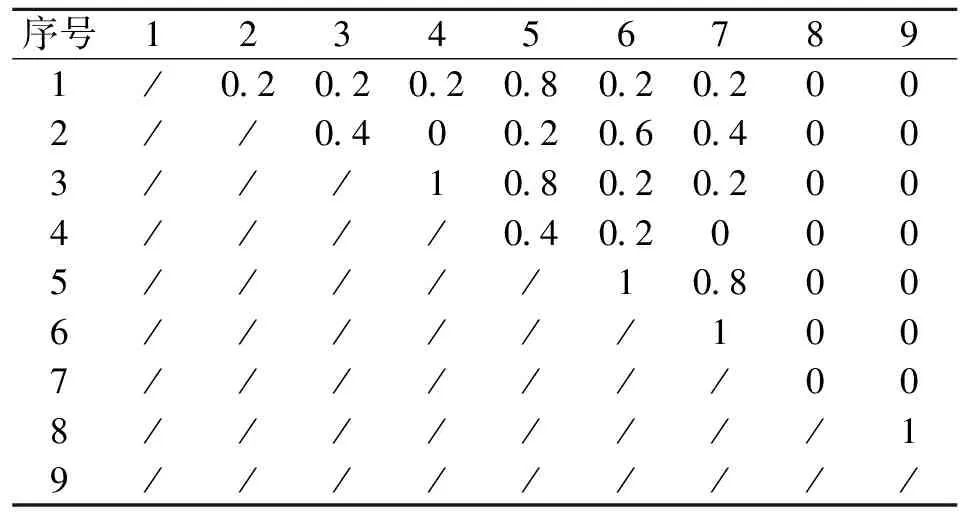
表6 bi,j分布矩阵

现对邻接需求强度和流通频率强度进行加权来求得综合强度，用fi,j表示：

(5)

式中ω1、ω2为加权系数，ω1取0.7，ω2取0.3。

计算得出综合强度的分布矩阵如表7所示。

表7 综合强度分布矩阵

据此可进一步确定各待布物之间的等级关系，等级对应的强度区间是{[0.8,1]，[0.6,0.8]， [0.4,0.6]，[0.2,0.4]，[0,0.2]}，可表示为{A,E,I,O,U}，则综合强度等级分布如图3所示。

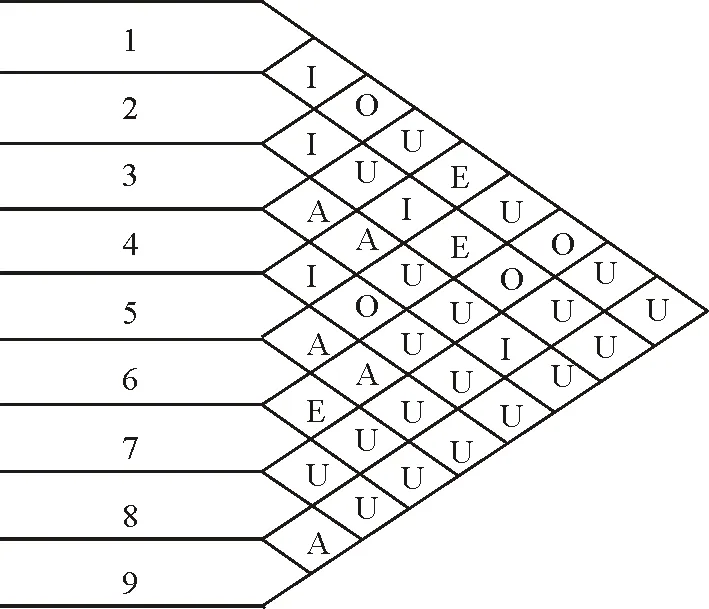
图3 综合强度等级分布Fig.3 Composite strength distribution

由图3可知，因A表示必须紧邻，由此可得到如下必须紧邻的关系：水槽与垃圾柜、灶台与调料柜、洗衣机与烘干机。由于冰箱柜一般放在离厨房入口最近处，故待布物1的位置可事先确定。根据上述得到的关系可将待布物3与4、待布物6与7、待布物8与9分别合并成一个功能模块，则可将原9个待布物简化为5个模块，如表8所示。

表8 整体厨房待布模块列表

布局时只需先优化出这5个待布模块的位置坐标即可。由SLP方法可得到这5个待布模块之间的综合强度等级分布如图4所示。

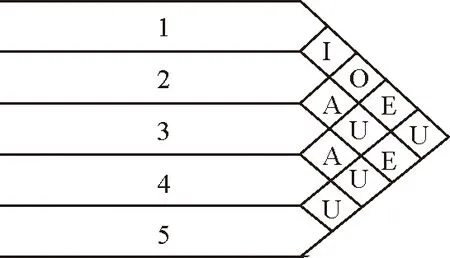
图4 待布模块综合等级关系图Fig.4 Composite strength relationship of objects

1.5 建立数学模型

1) 目标函数一。两待布物的紧邻需求越高，则间距越小，其数学模型可表示为：

(6)

(7)

式中，di,j为两待布物i与j中心点间的线性路线总长，其他符号意义同前。

2) 目标函数二。将炊事行为路线简化为：贮存区(储存食物、炊具、调料等)——准备区(摘理、清洗、切备等)——烹饪区(烹饪、存放等)，三个区之间的距离要保持动线短、不重复、作业性能好的合理间距，最理想的工作路线是呈三角形，即所谓的“三角形工作路线”，才能使工作效率达到最高。每两个区的中心点连线可以看作是三角形的边，优化目标是要满足人的炊事行为工作路线最短，即三角形三边之和最小，可用式(8)表示：

(8)

式中X={(x1,y1),(x2,y2), …,(x5,y5)}为待布模块的形心坐标，i,j,k∈[1,5],且i≠j≠k。

综上所述，整体厨房产品布局优化问题可以归纳为多目标优化问题，其数学模型为：

式中X=(X1,X2,…,Xn)∈Rn为n维决策变量，f=(f1,f2,…,fm)是目标函数，包含一个或多个目标数；fk(X):Rn→R,(k=1,2,…,m)表示第k个目标函数；gi(X)和hj(X)分别为不等式约束和等式约束。X为决策变量的可行域,其表达式为：

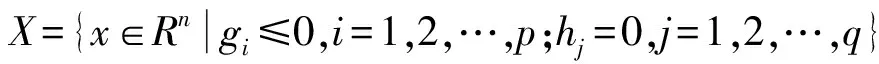
此模型有两个目标函数，用求解多目标优化问题的传统方法可解决[9]，此处用线性加权法对式(6)和式(8)进行线性加权求和，得：

λ2[(xi-xj)2+(yi-yj)2+(xj-xk)2+

(yj-yk)2+(xk-xi)2+(yk-yi)2]}

(9)

2 求解过程与方案评价

2.1 用改进粒子群算法求解

为了进一步提高求解效率及均衡粒子在搜索空间里的探索能力与开发能力，本文采用文献[10]中非线性动态调整惯性权重与学习因子的方法对标准PSO算法进行改进。

每次迭代中ω为：

(10)

式中，ωs为惯性权重的迭代初值，ωe为惯性权重的迭代终值，t为当前迭代次数，tmax为最大迭代次数。

学习因子随迭代的进行而动态变化：

(11)

(12)

式中，c1s和c1e分别表示c1的迭代初值和迭代终值，c2s和c2e分别表示c2的迭代初值和迭代终值，其它符号含意同前。

采用改进粒子群算法对适应度函数(9)进行求解，参数设置如下：种群规模为40，迭代200次[11]，ωs=0.4,ωe=0.9，c1s=2.5，c2s=0.5，c1e=0.5，c2e=2.5。由计算结果可得到若干组解。从理论上来说，这些解都是有效解，但不一定是最优解。整体上看，由于其它有效解的优化极值偏大或偏小，故选取其中8组优化极值分布于区间[6000,9000]的解作为备选方案，从中选取最优解，如表9所示。

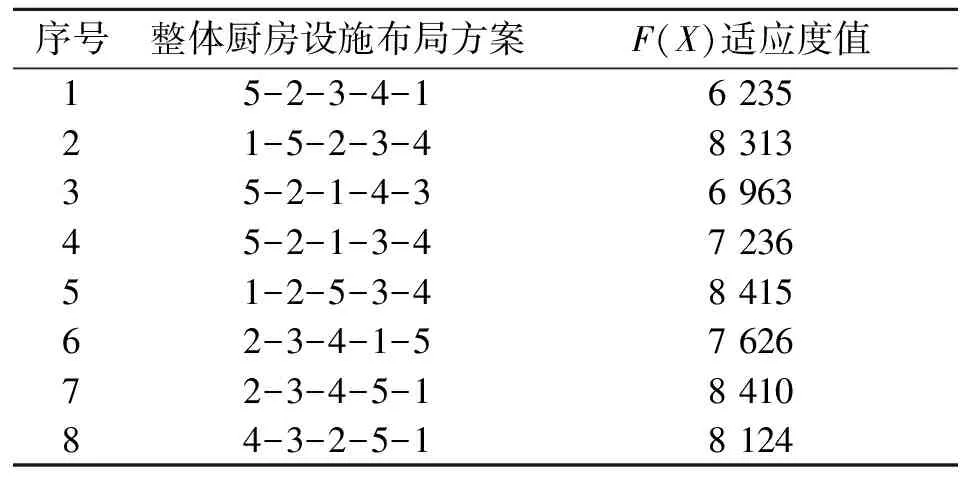
表9 整体厨房产品布局Pareto备选方案

2.2 方案评价与择优

求解运算后得到以上方案的适应度值，但是不能直接依据适应度值来判断方案的优劣，而是应该结合实际，充分考虑产品之间的紧邻关系需求，即SLP分析结果。

基于综合关系强度分析得出的厨房产品邻接需求和位置约束，可用于对上述方案进行对比与评价，以确定相对最优方案。

SLP分析中，综合等级为A的有：待布模块2与3、3与4，上述备选方案中，方案1、2、6、7均满足这个条件，可以优先考虑。综合等级为B的有：待布模块2与5、1与4，满足这个条件的有方案1和3。

由此可以判断出方案1为满足以上条件的交集。同时，这5种方案在适应度值方面也高于其它方案，说明其紧邻关系与综合关系强度是协调的，因此方案1、2、3、6、7均为可行方案。

这5种方案的适应度曲线图如图5所示，其中方案1的适应度值和收敛迭代次数最小，并且其迭代过程具有明显的优越性，应为5个可行方案中相对最优的方案，其位置坐标如表10所示，参照其坐标值的平面布置如图6所示，符合室内设计原则。

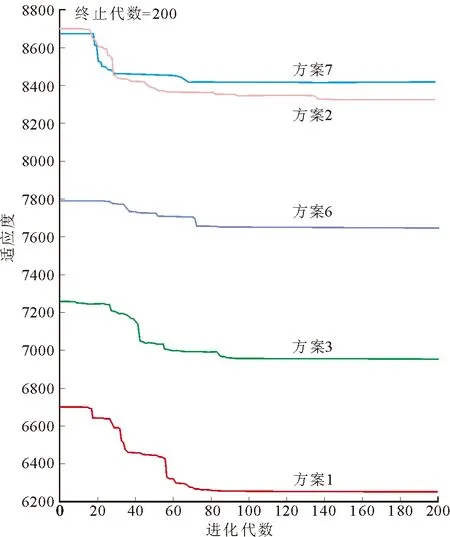
图5 方案1、2、3、6、7适应度曲线Fig.5 Fitness curves of plans 1, 2, 3, 6 and 7

优化方法设计变量坐标值/mm目标函数IPSO(x1，y1)(5050，849)(x2，y2)(3749，2687)(x3，y3)(4617，2650)(x4，y4)(5087，1827)(x5，y5)(2325，2744)6325

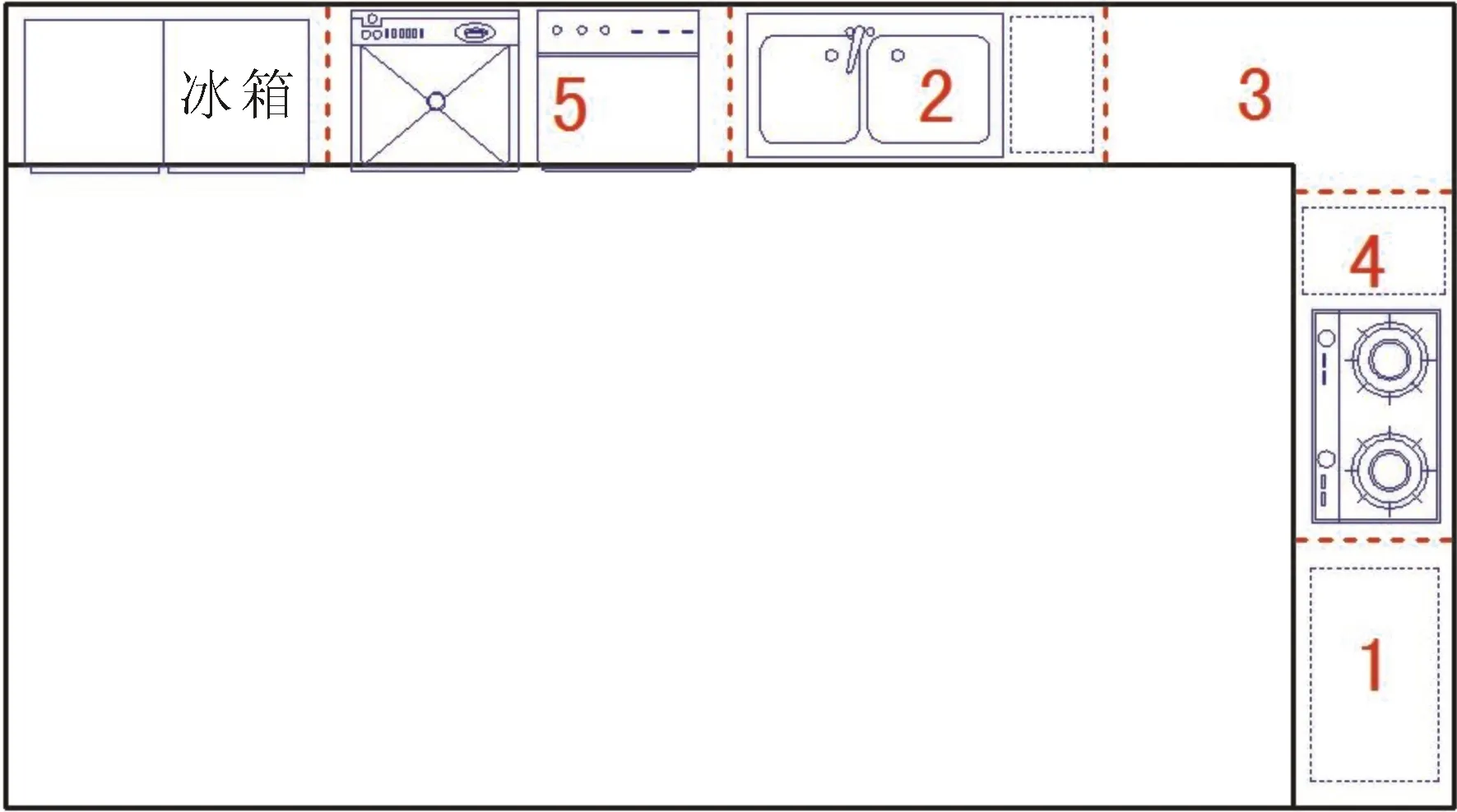
图6 相对最优布局方案Fig.6 Relative optimal layout

以上分析是针对典型UK家事型整体厨房实例进行L型布局时得到的较优方案，在客户需求不同时，即要求厨房形式为K型独立式、DK型餐事型或LDK型起居式时，还需选择不同的参与布局物体集合，按照以上思路来生成不同的布局方案。由于篇幅有限，在以后的研究中将进一步论述。

3 结 语

由于产品布局优化问题常具有多态性、模糊性和主观性，很难用精确的数据来评价。本文以整体厨房产品为例，引入SLP方法分析产品之间的综合关系，为了进一步提高求解效率，采用改进粒子群算法进行优化求解，最终得到产品的最佳布局方案。本文仅以一种具有代表性的家庭厨房布局形式为例，在后期的研究中，还需要针对不同客户需求考虑更多的产品模块，以及不同厨房平面的多种布局形式。此外，该方法还可以尝试应用到陈设用品布局、舱室布局、生产系统布局等方面。

[1]王运龙,王晨,纪卓尚,等.船舶居住舱室智能布局优化设计方法研究[J].中国造船,2013,54(3): 140-145.

WANG Yunlong,WANG Chen, JI Zhuoshang,et al. Study on intelligent layout design of ship cabin[J]. Shipbuilding of China, 2013,54(3): 140-145.

[2]李云,龚昌奇.改进的遗传算法在游艇舱室布局优化设计中的应用[J].航海工程,2010,39(1): 34-37.

LI Yun,GONG Changqi.Application of improved genetic algorithms in the optimization design of yacht cabin’s layout.[J].Ship&Ocean Engineering,2010,39(1):34-37.

[3]BUKOWSKI R W,SEQUIN C H. Object associations: a simple and Practical approach to virtual 3D manipulation [C]//Proceedings of Symposium on Interactive 3D Graphics. New York: ACM Press,1995:131-139.

[4]SMITH G, SALZMAN T, STUERZLINGER W.3D scene manipulation with 2D devices and constraints [C]//Proceedings of Graphics Interface. Toronto:Canadian Information Processing Society Press,2001:135-142.

[5]陈光明,李桂清,刘培,等.家居布局的层次化约束及粒子群优化[J].计算机辅助设计与图形学学报, 2014,26(10):2-8.

CHEN Guangming, LI Guiqing, LIU Pei, et al. Hierarchical constraints with particle swarm optimization for furniture arrangement[J]. Journal of Computer-Aided Design and Computer Graphics, 2014,26(10):2-8.

[6]高瞩,吉晓民,张春强.基于广义有向图的产品设计风格描述方法研究[J],西安理工大学学报,2010,26(2):181-184.

GAO Zhu, JI Xiaomin, ZHANG Chunqiang. Research on the descriptive method of topological relationships in product from prototype based on generalized directed graph[J]. Journal of Xi’an University of Tecnology, 2010,26(2):181-184.

[7]刘昕,余隋怀,初建杰,等.改进PSO的飞机驾驶舱组合排序人机布局优化[J].计算机工程与应用,2015,51(7):1-6.

LIU Xin, YU Suihuai, CHU Jianjie,et al. Airplane cockpit ergonomic layout optimization based on improved PSO algorithm combining grouping and ranking[J]. Computer Engineering and Applications, 2015,51(7):1-6.

[8]胡耀,姜治芳,熊治国，等.基于SLP和遗传算法的容积型船舶内部舱室位置布局设计优化[J].中国舰船研究,2013,8(5):20-26.

HU Yao, JIANG Zhifang, XIONG Zhiguo, et al. The optimized layout design of volume type ship cabins based on SLP and GA[J]. Chinese Journal of Ship Research, 2013,8(5):20-26.

[9]郑金华.多目标进化算法及其应用[M].北京:科学出版社,2007.

[10]魏锋涛,宋俐,李言,等.基于改进粒子群算法的四辊压机机座结构优化设计[J].中国机械工程,2012,23(19):61-65.

WEI Fengtao, SONG li, LI Yan, et al. Optimal structural design of 4-roller rolling mill frame based on an IPSO algorithm[J]. Chinese Mechanical Engineering, 2012,23(19):61-65.

[11]李丽,牛奔.粒子群优化算法[M].北京:冶金工业出版社,2009.

(责任编辑 王卫勋)

Research on product layout optimization method based on SLP and improved particle swarm optimization algorithm

SUN Xin1,2, JI Xiaomin1,2, WANG Yi1

(1.School of Mechanical and Precision Instrument Engineering, Xi’an University of Technology，Xi’an 710048,China; 2.School of Art and Design, Xi’an University of Technology, Xi’an 710048,China)

The products layout design requires that all products can meet certain constraints, and can reach the highest work efficiency in a certain space. From the optimization point of view, this problem can be seen as a layout problem in combinatorial optimization. In consideration of the products’ relationship, size and direction, this paper uses the system layout planning method and sets up a mathematical model for integral kitchen products as a case study. By the IPSO method, the products layout optimization design is achieved, providing an effective way to solve these problems. This can be popularized to furniture, furnishing, cabin, production system layout design and so on.

products; layout; optimal design; system layout planning (SLP); improved particle swarm optimization

10.19322/j.cnki.issn.1006-4710.2016.04.019

2015-10-10

陕西省教育厅自然科学基金资助项目(14JK1532)；陕西省自然基金面上资助项目(2016JM5091)；西安理工大学科学研究资助项目(2015RWYB007)

孙昕，女，讲师，博士生，研究方向为产品设计、室内设计。E-mail:sunxin0327@126.com

吉晓民，男，教授，博导，研究方向为产品设计。E-mail:jixm@xaut.edu.cn

TH122

A

1006-4710(2016)04-0488-06