反应加速度法在地下结构抗震分析中应用解析

文/赵志强 辽宁省交通规划设计院有限责任公司 辽宁沈阳 110000

反应加速度法在地下结构抗震分析中应用解析

文/赵志强 辽宁省交通规划设计院有限责任公司 辽宁沈阳 110000

结合实际工程，运用反应加速度法，分析了地下结构在设计地震和罕遇地震下的抗震性能，并通过算例展示了反应加速度法在隧道抗震设计中的运用，指出地下结构的内力不受地震工况控制，在设计地震作用下，隧道处于弹性工作状态，在罕遇地震作用下，隧道满足局部进入塑性工作状态的要求。

地下结构；反应加速度法；抗震性能；静力荷载

1、反应加速度法基本原理

反应位移法属于荷载-结构法，考虑了三种荷载:地震土压力、土-结构接触面的剪切力以及惯性力。而反应加速度规则属于地层-结构法，需要建立土层-地下结构全体计算模型，那么地震土压力和剪切力则属于系统的内力，此刻仅需考虑惯性力。而惯性力则取决于系统的质量分布和加速度值，在土层-地下结构系统断定的情况下，系统质量分布是断定的，因而只需断定加速度分布规则。关于地下结构而言，其最不利状况为结构顶板、底板发作最大相对变形，运用该时间自由土层剪应力分布计算有效反应加速度。ρi为第i层土单元的密度;该时间第i层土单元的运动方程为

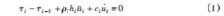
式中:τi-1，τi分别为地下结构发作最大变形时第i层土单元顶部与底部的剪应力;hi为第i层土单元的厚度;ci为介质阻尼系数;üi，ui分别为第i层土单元加速度和速度。经过式(1)中的应力项计算有效反应加速度

式中:ai为第i层土单元水平反应加速度。

2、反应加速度法的计算过程

根据上述基本原理，可概括总结反应加速度法的计算过程主要包含:

建立自由场模型;进行一维土层地震响应分析，断定地下结构发作最大相对变形或地上与基岩发作最大变形的时间;获取该时间各分层处的剪应力;建立土体-地下结构全体计算模型(地层结构模型);关于土体的分层，由式(2)计算每层的水平加速度;将得到的各层水平加速度施加在计算模型上，计算结构的内力与变形。关于第二步一维土层地震响应分析，现在一般运用SHAKE软件，但该软件运用起来较为杂乱，如单位变换、土层细化等，工程设计人员运用较为麻烦。此刻可采用反应位移法中推荐的土层位移沿深度的改变规则以及由此断定的剪切力计算式

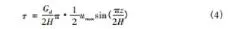
式中:z为土体深度;u(z)为土体任一深度的水平位移;umax和H分别为地表最大水平位移与土体计算深度，均依据《城市轨道交通结构抗震设计规范》(GB50909—2014)选择，Gd为土体的动剪切模量;τ为土体的剪应力。

3、算例分析

以某地下双层双跨的结构地铁车站结构工程为例，该结构宽22.7m，高14.0m，混凝土弹性模量300MPa，泊松比0.25，密度2 500kg/m3。结构顶板厚0.8m，底板厚1.0m，侧壁厚0.8m，上覆土层厚3.0m。反应加速度法计算模型，土层特性参数，见表1。

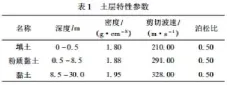
3.1土层变形计算。运用式(3)计算土层的变形，其间:umax为地表与基准面的相对最大位移，由《城市轨道交通结构抗震设计规范》(GB50909—2014)的表5.2.4-1和表5.2.4-2断定，假定地轰动峰值加速度为0.1g，设防烈度为7度，则设计地轰动峰值位移umax为0.07m，H为土层计算深度，取30m，z为土层深度，则可从底板开始顺次向上计算土的位移。

3.2土层剪切力计算。运用式(4)可断定每层分层土外表的剪切力，这篇文章仅给出了天然土层分层处的剪切力及由此断定的加速度值，见表2。

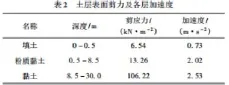
3.3计算结果分析。本文计算运用大型通用软件ANSYS，其中对于分层土体水平加速度采用cmacel命令分层施加。

3.3.1结构变形。最大水平位移1.67mm，出现在左侧墙上半部分，最大竖向位移3.01mm，出现在底板跨中。

3.3.2结构弯矩。结构弯矩最大值为1100kN·m，出现在结构底板以及中柱与侧墙交接处。

3.3.3结构剪力。结构剪力最大值约665kN，出现在结构底板以及中柱与侧墙交接处。

3.3.4结构轴力。结构轴力最大值约1230kN，出现在中柱下段，但在结构顶板上出现了少量的拉力(正的轴力值)，这是对结构极为不利的。结构的四个角的变形和承受的力都较大，处于不利地位。但结构最不利的位置是在结构底板以及中柱与侧墙交接处。另外，在结构顶板上出现了少量的拉力(正的轴力值)，这是对结构极为不利的。

4、与反应位移法的比较

笔者也采用了反应位移法对该相同地下结构进行了计算分析，限于篇幅，仅给出由反应位移法得到的结构变形和弯矩。通过与反应加速度法计算结果的比较，有如下结论:

4.1两种方法得到的结构变形和变形规律基本上一致，区别仅在于内力和变形幅值的大小，由此可见，两种办法均可用于地下结构抗震分析。因此，我国的标准《城市轨道交通结构抗震规划标准》(GB50909—2014)也清晰引荐该两种办法作为地下结构抗震分析办法;

4.2由于两种办法得到结构内力和变形幅值上的区别，可从两种办法的基来源理入手分析。反应位移法属于荷载-结构法，其间荷载又是通过变形直接得到，因此没有考虑周围土体与地下结构间的动力相互作用;而反应加速度规律属于地层-结构法，建立土体-地下结构全体相互作用计算模型，能考虑地下结构与周围土体的相互作用。因此，反应位移法计算得到的结构地震响应偏小，这对于工程规划是不利的;

4.3从办法的适用性角度来看，反应位移法适用于结构模型简略、规律的地下结构，由于结构一旦复杂，土绷簧参数的取值非常困难;另外，如若还需考虑围护结构的作用，则愈加难以处理。而反应加速度规律可适用于不规律断面，也能够考虑围护结构等，因此其适用范围广，且计算结果偏大，有利于结构的抗震安全。

结语：

本文运用反应加速度法，结合实际工程，分析了地下结构在设计地震和罕遇地震下的抗震性能。反应加速度法可以较好的运用到隧道抗震设计中，地下结构的内力不受地震工况控制，在设计地震作用下，隧道处于弹性工作状态，在罕地震作用下，隧道满足局部进入塑性工作状态的要求。本文的论述可为相对工程提供参考。

［1］小泉淳.地下结构的抗震研究及算例［M］.张稳军，袁大军，译.北京:中国建筑工业出版社，2013.

［2］董正方，王君杰，姚毅超.深埋地下结构抗震设计方法评价［J］.振动与冲击，2013，31(19):79-85.

［3］李新星，陈鸿，陈正杰.地铁车站结构抗震设计方法的适用性研究［J］.土木工程学报，2014，47(2):322-327.