一元四次整系数多项式的因式分解法
戴中林
(西华师范大学数学与信息学院,四川南充637002)
一元四次整系数多项式的因式分解法
戴中林
(西华师范大学数学与信息学院,四川南充637002)
仅对一元四次整系数多项式在实数域内分解问题进行了研究,根据分解后其系数应为二次代数整数的特点,以及导出的二次方程判别式的完全平方性质,得出了一元四次整系数多项式在实数域内能分解成两个二次因式乘积的条件及方法,从而解决了一元四次整系数多项式在实数域内的因式分解问题.
整系数多项式; 完全平方数; 因式分解; 实数域; 二次代数整数
1 引 言
对于一般高次方程的解法,相关教材上已有介绍[1-3].三次方程可用卡当公式求解,而四次方程
x4+ax3+bx2+cx+d=0,
(1.1)
则可由费拉利法求解.其方法是先引入参数y将(1.1)式配成平方差,再由二次式的完全平方性质,令其判别式等于零,可得一个关于参数y的整系数三次方程
y3-by2+(ac-4d)y-[(a2-4b)d+c2]=0.
(1.2)
当此方程求出一个整数解y后,则四次方程(1.1)可由下式分解
(1.3)
一般情况下,三次方程(1.2)中的常数项数值较大,求解较为麻烦.例如分解四次方程(文中例5)
x4+8x3+18x2+116x-26=0.
首先由公式(1.2)得到三次方程
y3-18y2+1032y-13664=0.
由于方程中常数项因数较多,可用长除法求其一个整根.即用常数项决定的所有的一次因式去逐一试除, 可得y=14.此解法虽然繁琐但是可行的,故应用费拉利法解四次方程的难点也就在于此.然后将整数解y=14代人(1.3)式即得分解式
对多项式而言,如果一个四次整系数多项式在实数域内是可约的,理论上我们只须用待定系数法将其分解成两个二次因式的乘积,并通过系数方程组求出这两个二次因式的所有待定系数即可.但实际上要仅由系数方程组直接求出这些待定系数是根本办不到的.通过研究得到,如果能通过多项式在不同范围分解后其系数的特点,则该四次多项式分解问题即可解决.关于一元四次有理系数多项式在其域内的因式分解问题,已在文[4]以及近年一些刊物发表的方法即文[5-8]进行了研究探讨,给出了一些解决的方法.而本文仅对四次整系数多项式在实数域内分解问题进行了研究,根据分解后其系数应为二次代数整数的特点,以及导出的二次方程判别式的完全平方性质,得出了一元四次整系数多项式在实数域内能分解成两个二次因式乘积的条件及方法, 从而解决了一元四次整系数多项式在实数域内的因式分解问题.
2 主要结果
2.1 一元四次多项式在有理数域上的因式分解[4]
定理1一元四次多项式在有理数域上可分解成
f(x)=x4+ax3+bx2+cx+d=(x2+A1x+B1)(x2+A2x+B2)
的必要条件是在常数项d中存在因数B1,B2,使得代数式T=a2-4b+4(B1+B2)为完全平方数.
由定理1可得一元四次多项式在有理数域上的因式分解法:
(i) 在常数项d=B1B2中确定一组因数B1,B2,使得代数式T=a2-4b+4(B1+B2)为完全平方数,设平方根为t≥0;
(iii) 确定An,Bn(n=1,2),使其满足A1B2+A2B1=c, 则四次多项式的分解式就能唯一确定.
例分解四次多项式 f(x)=x4-11x3+27x2-39x+18.
解由定理1
t2=a2-4b+4(B1+B2)=13+4(B1+B2)≥0,
有B1+B2≥-3.又由B1B2=18,当取B1=±1,±2,±3, 则B2=±18,±9,±6, 故有B1+B2=19,11,9.仅当B1+B2=9时,有t=7;由公式
且当 A1=-2,A2=-9,B1=3,B2=6时,有A1B2+A2B1=-39=c成立.故分解式为
f(x)=(x2-2x+3)(x2-9x+6).
2.2 一元四次整系数多项式的在实域内的因式分解
定义1若数ξ满足一个首项系数为1的n次整系数(或有理系数)代数方程f(x)=0,则称ξ为一个n次代数整数(或代数数).


证因ξ为二次代数整数,由定义1,设数ξ满足二次整系数方程x2+2ax+b=0,故由求根公式


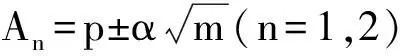
引理2任意两个二次代数整数乘积为整数的充要条件是这两数应为二次共轭代数整数.

为整数.又m,s均为不含平方因数的非零整数,故仅当s=m以及p1α2+p2α1=0时,有A1A2的整数性质成立.
当s=m时

当p1α2+p2α1=0时,取p2=p1,则有α2=-α1,这时
故两实数应为


引理3若一元四次整系数多项式在实数域内可分解成
f(x)=x4+2ax3+bx2+cx+d=(x2+A1x+B1)(x2+A2x+B2),
则其中系数分别为两组共轭代数整数

证由待定系数法,可得系数方程组

由(2.1),(2.2)式知Ai(i=1,2)满足整系数二次方程
A2-2aA+[b-(B1+B2)]=0.
由定义1及引理1,引理2有
为一组二次共轭代数整数;同理由(2.2),(2.4)式知
为另一组二次共轭代数整数.
将上述任一组结果代入(2.3)式有
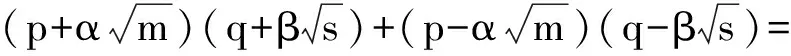
即

因m,s均不含平方因数的非零整数,故当s=m时,则上式整数性质成立.故

又

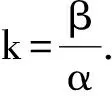

定理2一元四次整系数多项式在实数域内可以分解成
f(x)=x4+2ax3+bx2+cx+d=(x2+A1x+B1)(x2+A2x+B2)
的必要条件是存在正整数k,使得代数式T=k4+(a2-b)k2+d为完全平方数.

由(2.6)式和(2.7)式消去m,得到关于未知量q的二次方程
q2-2k2q=(p2-b)k2+d.
即
(q-k2)2=k4+(p2-b)k2+d.
有
因q为整数,故存在正整数k,使得代数式 T=k4+(a2-b)k2+d为完全平方数.
由定理2可得四次整系数多项式在实域内的因式分解法:
(i) 在代数式T=k4+(a2-b)k2+d中确定正整数k,使其为完全平方数,设平方根为正整数t;
(iii) 确定An,Bn(n=1,2),使其满足 A1B2+A2B1=c,则四次多项式的分解式就能唯一确定.
本定理需要说明几点,一是当四次多项式中三次项系数不为偶数2a时;或T不为完全平方数时;或系数方程组(Ⅰ)无整数解时,则该四次多项式在实数域内就不可约.二是当m<0时,则分解式中的待定系数An,Bn的范围将从实数域扩大到复数域.三是当k取正有理数时定理2也是成立的.四是定理2中多项式系数也可推广到有理数域.
3 例 子
例1分解四次多项式f(x)=x4+6x3+16x2+54x-23.
解由定理2
p=a=3, t2=k4+(a2-b)k2+d=k4-7k2-23≥0,
当取k=4时,t=11;则 q=k2-t=5, m=(a2-b)+2q=3,故


故分解式为

例2分解四次多项式f(x)=x4+10x3+34x2+42x+21.
解由定理2 ,p=5;t2=k4-9k2+21≥0,当取k=2时,t=1;则
q=k2-t=3, m=p2-b+2q=-3,
故待定系数



例3分解四次多项式f(x)=x4+8x3+18x2+116x-26.
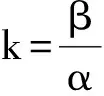
则
q=k2+t=7, m=(a2-b)+2q=12.
故有

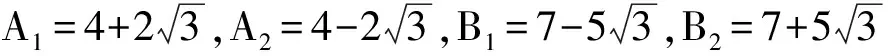

[1] 余介石, 陆子芬.高等方程式论[M].北京:商务出版社,1951:21-35.
[2] 余元庆.方程论初步[M].上海:上海教育出版社,1964:102-107.
[3] 李世雄.代数方程与置换群[M].上海:上海教育出版社,1983:4-13.
[4] 戴中林.四次有理系数多项式的一种因式分解法[J].西华师范大学学报(自然科学版),1984(1):82-86.
[5] 陈焕良, 张筱林.关于高次多项式的因式分解[J].大学数学,1994,10(4):66-68.
[6] 姜豪.再谈高次多项式的因式分解[J].大学数学,1996,12(3):103-104.
[7] 马敏.一个关于多项式函数的因式定理[J].大学数学,2001,17(2):101-103.
[8] 盛兴平.实系数一元四次方程的矩阵解法[J].数学通报,2002(12):37-38.
[9] 闵嗣鹤, 严士健.初等数论[M].北京:高等教育出版社,2001:153-164.
A Quartic Polynomial Decomposition Method in the Real Domain Factod
DAIZhong-lin
(School of Mathematics and Information, China West Normal University, Nanchong Sichuan 637002, China)
Integral coefficient quartic polynomial in the real domain decomposition sometimes derived and related to a yuan quadratic equation discriminant type integer nature, gives the integral coefficient quartic polynomial of a factor decomposition method to solve the integral coefficient quartic polynomial in the real domain factorization problem.
quartic polynomial of integer coefficient; square number;factoring; real number field; conjugate algcbraic nuber
2016-05-14
戴中林(1949-),男,学士,副教授,从事微分方程方向研究.Email:dzl47519@126.com
O151.1
C
1672-1454(2016)06-0101-05

