基于多源水深数据融合的海底高精度地形重建

樊妙，孙毅，邢喆，王祎婷，李四海 ，金继业

(1．国家海洋信息中心，天津 300171)



基于多源水深数据融合的海底高精度地形重建

樊妙1，孙毅1，邢喆1，王祎婷1，李四海1，金继业1

(1．国家海洋信息中心，天津 300171)

本文在研究多源水深数据构建技术的基础上，分析了张力样条插值算法和“移去-恢复”法的多源水深数据融合处理技术，基于该方法选取实验区，利用多波束、单波束、历史海图等多源水深数据进行高精度海底地形融合试验，并针对多源水深融合技术缺少误差评估的现状，利用split-sample方法对融合结果进行水深不确定性评估，形成融合结果的可靠性空间分布。结果表明该方法无论是在数据稀疏区还是高密度区都达到了较好的融合效果，既保留了高分辨率水深数据的细节信息，又较真实的反映了研究区海底地形特征，且构建的海底地形精度可靠，误差百分比集中在0.5%。本文整套数据融合和结果评估方法可为多源水深数据融合的海底高精度地形构建提供借鉴和参考。

多波束；多源水深数据融合；张力样条算法;split-sample

1 引言

海底地形数据是开展海洋地球物理、海洋生物、海洋化学及海洋地质等学科研究的基础[1]。自20世纪50年代海洋测深技术广泛应用以来，尤其是多波束技术的应用，实现了高精度、大面积、高效率的海底地形获取，然而大部分的海底地形仍然处于未勘测状态[2]。Vogt等(2000年)估算，利用当前的测量设备需要耗费900个测量年才能完全覆盖整个世界大洋。因此，当前充分利用各种不同历史时期、不同来源、不同分辨率的水深数据进行集成和融合，不仅是获取全面反映海底DBM(Digital Bathymetric Model)的有效途径，也是当前水深数据处理研究的热点。

随着多源水深数据的日益增多，无论是大尺度的数据集成，还是小规模的融合应用，就目前相关文献来看，大部分学者对于水深数据的融合方法主要基于综合利用张力样条插值法、loess插值法以及kriging插值或对上述方法进行改进和综合应用的基础上建立起来的[3—10]，如Jakobsson等[11]和Arndt等[12]融合历史水深数据、单波束、多波束及等深线数据，全面反映南北极水下地形概况，GEBCO融合全球测深数据、历史存档数据、卫星测高数据形成全球1′、30″格网数据，所用张力样条插值方法较好地解决了数据融合问题，但是缺乏精度评估体系；Jha等[13]基于多点地质统计模型，利用不同时期多波束和单波束水深数据，形成密西西比河圣路易河段的水下地形，该方法目前较为新颖，利用训练图像突破了传统两点地质统计的空间相关局限性，能够较好地反映地形特征，但是融合结果高度依赖于训练图像，而合适的训练图像不易获得。

本文在分析国外水深数据融合方法的基础上，对近岸地区多波束和单波束无法达到的数据测量空白区，结合大比例尺海图数据、历史存档水深数据，基于张力样条插值算法，采用“移去-恢复”法[9,11—12,14]，对多源水深数据进行了融合处理，形成了试验区全覆盖的高精度海底DBM，既保留了高分辨率水深数据的细节信息，又较详细地反映了研究区海底地形特征。同时，针对Hell 和Jakobsson[9]，Jakobsson等[11]以及Arndt等[12]并未对用“移去-恢复”法生成的模型进行误差评估的缺陷上，利用split-sample方法对形成的海底DBM进行了插值不确定性分析，不仅从统计模型和空间分布上分析了融合方法造成的海底地形误差，而且也增强了数据后期使用的可靠性和信任度。本方法的应用可对我国专项调查和历史存档水深资料的融合处理提供借鉴和参考。

2 数据与方法

2.1 研究区域及数据组成

本研究区选取中国近岸某海域，该区域内有两条开挖航道，总体海底地形平缓，水深最深处为22 m。由于该区域具有明显的人工开凿痕迹，且不同来源的水深数据较为丰富，适合于本次融合方法的试验。其中，多波束数据精度较高，但离岸边较远，分布在5 m以深海域；单波束数据测线间距较大，主要集中在北部5 m以浅海域；海图水深点稀疏，但在近岸分布密集，且与多波束数据有一定重复，在近岸为主要融合数据源；矢量化水深数据比例尺较小，可作为补充数据。考虑到该地区为港口区域，由于航道人工开挖等原因，不同期的水深地形有可能存在差异，因此本区域所选海图数据及多波束水深调查数据时间应相近，尽量保证数据的一致性。由于上述数据时间相近，在数据融合过程中，首先以多波束和单波束实测数据为准，在近岸实测数据空白区以海图水深数据为准。研究区位置及数据覆盖情况如图1所示。

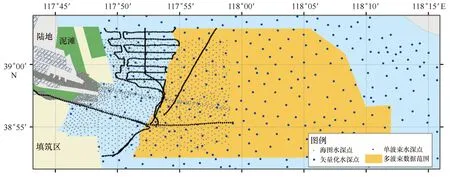
图1 研究区地理位置及数据分布Fig.1 Location of the study area and the coverage of data source

船测水深来自于我国近海海洋综合调查与评价专项，调查时间为2008—2009年，多波束采集仪器为Reason Seabat8101，单波束测深仪为HydroTrack，两种数据均经过各种改正处理，归算至理论深度基准面；海图数据共3幅，由海司航保部出版发行，具体信息如表1；矢量化水深数据由海司航保部生产，后经国家海洋信息中心综合整理而成，比例尺为1∶10万。

表1 使用海图数据一览表

2.2 研究方法

2.2.1 张力样条插值算法

由于船测水深数据是沿着船舶测量航迹线分布的，尤其是单波束水深测量，航迹线以外存在大量的数据空白区域，常规的插值算法会在数据稀疏区形成假值，不适合于稀疏数据的海底DBM构建，因此双三次样条插值算法在早期得到了广泛的应用。该算法精确通过已知点，且能得到光滑的曲面，但其也存在致命缺陷，即在地形急剧变化或坡折地带，光滑的特性反而掩盖了地形本来的不连续特征[9]。Smith和Wessel通过大量的地形特征验证了双三次样条插值算法的缺陷，通过张力因子，进一步控制了已知点间插值超限的现象[15]，使结果优于普通样条函数插值。目前张力样条函数是构建海底DBM的标准插值算法[16]，也是众多插值算法中精度较高的[17]。本文在数据稀疏区域应用张力样条插值方法实现海底地形的构建。

2.2.2 基于“移去-恢复”法的多源水深数据融合

由于多源水深数据的密度差异较大，利用常规插值法在沿航迹分布的单波束水深以及密度较大的多波束水深区域附近极易出现地形假值，因此好的融合方法体现在既能够保留高密度水深数据的细节信息，又能够避免稀疏数据区域插值方法导致的异常假值[18]，“移去-恢复”法的应用即是解决上述问题。该方法首次由Forsberg和Tscherning进行了详细的论证和推导，并应用在重力场模型构建中[17]，随后Hell和Jakobsson[9]以及Smith和Sandwell[14]将其应用在多源海底地形模型构建中取得了较好效果。“移去-恢复”法主要采取两个步骤，在移去阶段，利用所有水深数据构建一个低分的水深格网，目的是为保证数据稀疏区的插值结果的正确性，然后将其重采样变换至所需分辨率作为基准网格，由于此阶段低分插值移去了数据稠密区的细节信息，因此在恢复阶段中，单独将稠密数据移去的部分(残差模型)进行恢复叠加至基准网格上。利用该方法，既能保证低密度数据不受高密度数据影响的独立性，又能克服高密度数据受低密度数据牵制而无法保留细节信息的缺点[9]。

2.2.3 基于split-sample方法的DBM精度评估

DBM数据误差主要为原始数据的误差和内插方法造成的误差[18]。在对本次插值结果进行精度评估时，暂且不考虑原始数据的误差，主要对插值模型导致的不确定性进行评估。目前，DBM的不确定性常通过中误差、平均误差、标准差等数值精度模型进行计算，但上述评估模型和方法需要选择合理的抽样检查点，难以对DBM的误差情况进行整体评价，且通过统计模型对指标进行加权评判，缺乏空间视角，没有顾及 DBM 误差的空间结构[19]。考虑到上述缺陷，本文利用split-sample方法[20]对插值结果进行不确定性分析，split-sample方法原理是通过随机抽取一定量的原始数据作为检测点不参与插值运算，而利用剩余的数据进行插值，最后计算检测点与插值点的差值并进行误差统计，重复上述步骤，直到每个点都进行误差统计计算为止，该方法通过统计每个点的插值误差能够全面反映插值模型的稳定性，衡量插值方法的可靠性[3](图2)。

图2 Split-sample方法原理Fig.2 Flowchart depicting the split-sample methodology for quantifying interpolation errors

2.3 方法应用

基于上述方法对试验区水深数据进行融合的技术流程如图3所示。数据融合的第一步是要将各种来源的水深数据进行前期预处理。船测水深数据经各项改正处理，剔除异常值；海图数据经过扫描、纠正和矢量化。其次，将所有水深数据统一空间基准、数学基础，统一数据格式，数据数学参考统一至WGS-84球面坐标系，理论深度基准面，数据格式均处理为ASCII XYZ，再对上述水深数据进行清理，去除异常值直至满意，最终输出为ASCII XYZ格式。

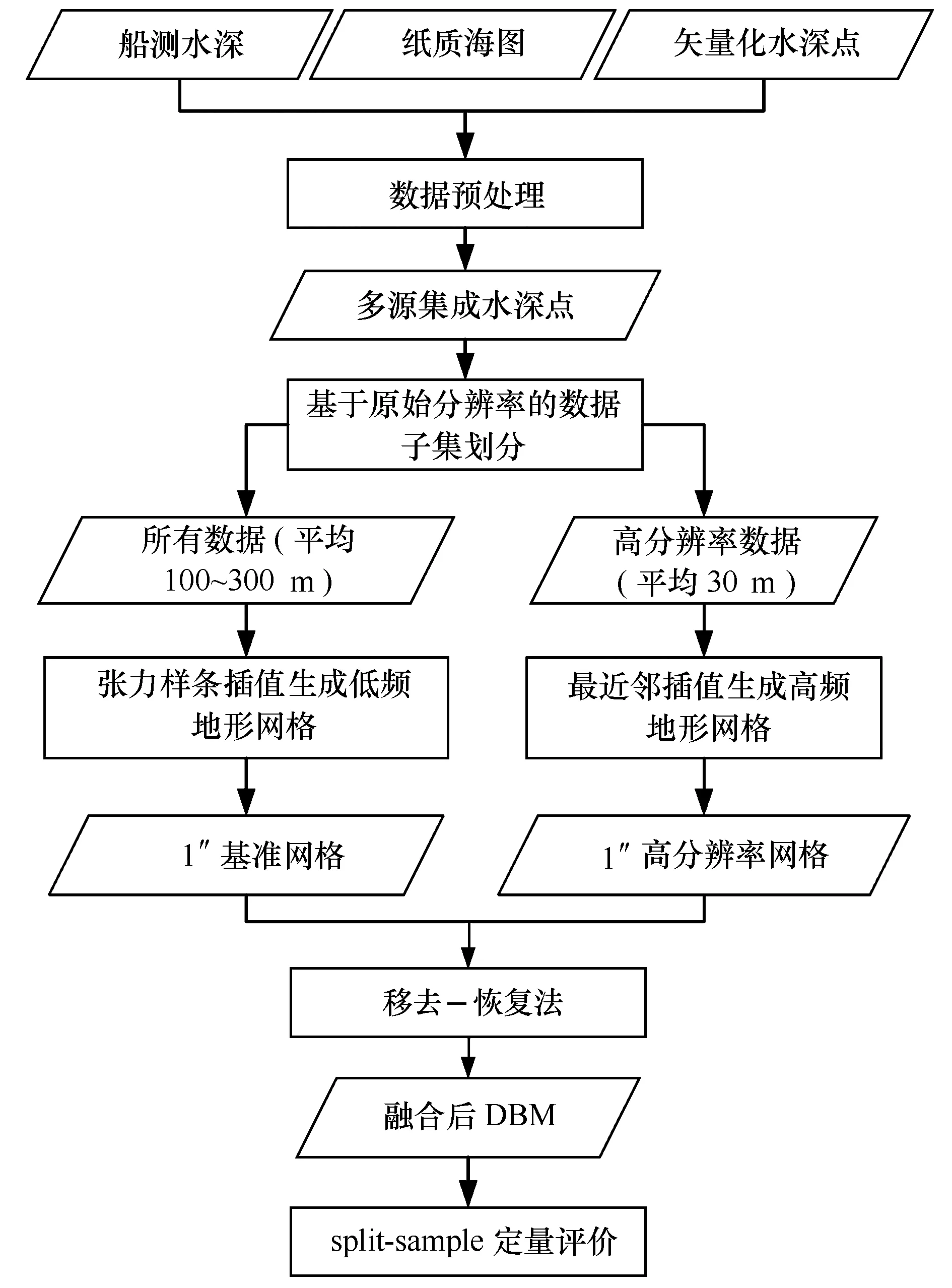
图3 基于移去-恢复法进行水深数据融合技术流程图Fig.3 Flowchart of the remove-restore bathymetric fusion techniques

对多源水深数据进行统一处理后，根据试验区数据分布密度进行数据子集划分后进行插值运算，该步骤分为两步：一步是针对所有数据采用张力样条函数插值法进行3″×3″格网插值，然后对插值结果重采样为1″×1″，将此结果作为1″基准网格数据；另一步，只针对高分辨率数据，应用最近邻插值法进行1″×1″格网插值，生成1″高分辨率网格。在插值前均要对插值数据进行块权重中值滤波，保证每个插值网格中只存在一个点，目的是滤除格网中其他潜在异常值的影响，避免产生震荡现象。

在插值网格的基础上，采用“移去-恢复”法[9,11—12,14]将低分辨率网格数据和高分辨率格网进行融合，具体操作步骤为：(1)将1″基准网格与1″高分辨率网格Z值进行比对，计算二者之间的差值，生成差值文件，内容包括经度、纬度、差值三列内容；(2)对差值文件采用最近邻法进行格网插值，格网大小为1″；(3)将差值网格和1″基准网格数据进行叠加合并，形成融合后的最终DBM。

最后，基于ArcObject，利用C#编写程序，实现split-sample方法对插值结果的精度评价。具体方法是对试验区所有数据先进行3″的块中值滤波操作，然后随机抽取10%的检测点，利用剩余的点进行移去-恢复法水深融合，重复上述过程，直至每个点都被统计到，最终计算控制点差值进行定量评价。

3 结果与评估

图4是利用本次融合方法生成的海底DBM，利用张力样条插值在数据稀疏区生成的海底地形光滑(如图4西边海图数据区)，同时在数据密度较大的区域保留了多波束数据更多的细节信息(图5)，两条开挖航道及航道周边的泥沙堆积特征明显(图4下方航道区)，利用近岸海图水深数据，填补了近岸长期存在空白数据的区域。该方法在数据接边区未产生理想效果，但是接边总体限差在规定范围之内(《GB 12327-1998海道测量规范》，测深范围在0～20 m时，极限误差为±0.3 m)。在研究区范围内，选取接边处限差最大剖面(图4 A-B)，从剖面图可以看出，利用“移去-恢复”法融合后，在水深约4.8 m处，限差为0.2 m，平均坡度为46%(图6a)，Hell提出的叠加法[9]，在水深约4.7 m处，限差为0.2 m，平均坡度为73%(图6b)，二者相比之下，前者在接边处限差小，且过渡较为平滑。在该区域中，数据的覆盖率只有44%，其余56%的面积均为数据空白区，其中单波束、海图水深数据及矢量化水深点约占0.8%，多波束水深数据约占43.2%。

由于多源水深数据融合的实施过程中运用了系列的方法和复杂的流程，Hell及Arndt等并未对插值结果进行不确定性评估，只是进行DBM融合部分细节进行对比[9,11—12]，Calder、Jakobsson利用蒙特卡洛方法对插值结果进行了评估[3,18]。本文利用split-sample方法对试验结果进行评估，其结果如图7所示。从图7a、7b可以看出误差与地形坡度和数据密度相关，在地形坡度相对较大但数据密度高的区域，误差较小，例如多波束数据覆盖的航道区域；地形坡度小，数据密度低的区域，同样误差较小，例如浅水平坦区域，这些区域总体误差控制在0.5%以下；而在地形坡度大，数据稀疏的浅水区航道区域误差稍高，误差百分比集中在4%左右，这些地方水深点较稀少，密度大致为200 m左右，误差比最大处分布在近岸A、B两处，其中A处误差比接近40%，B处接近25%，通过分析原始数据点分布，发现上述两处出现最浅点(图7c，7d)，水深与周边水深反差较大且距离平均约200 m，超过块中值滤波3″(90 m)的距离，因此块中值滤波并未起作用，导致震荡现象产生；而相反在C处，同样是浅点，但该处水深间距平均为60 m，块中值滤波的应用(如图7e红色三角点)避免了震荡现象的产生。

图4 最终海底DBMFig.4 Final DBM after integration

图5 细节对比Fig.5 Comparison of small details based on remove-restore method

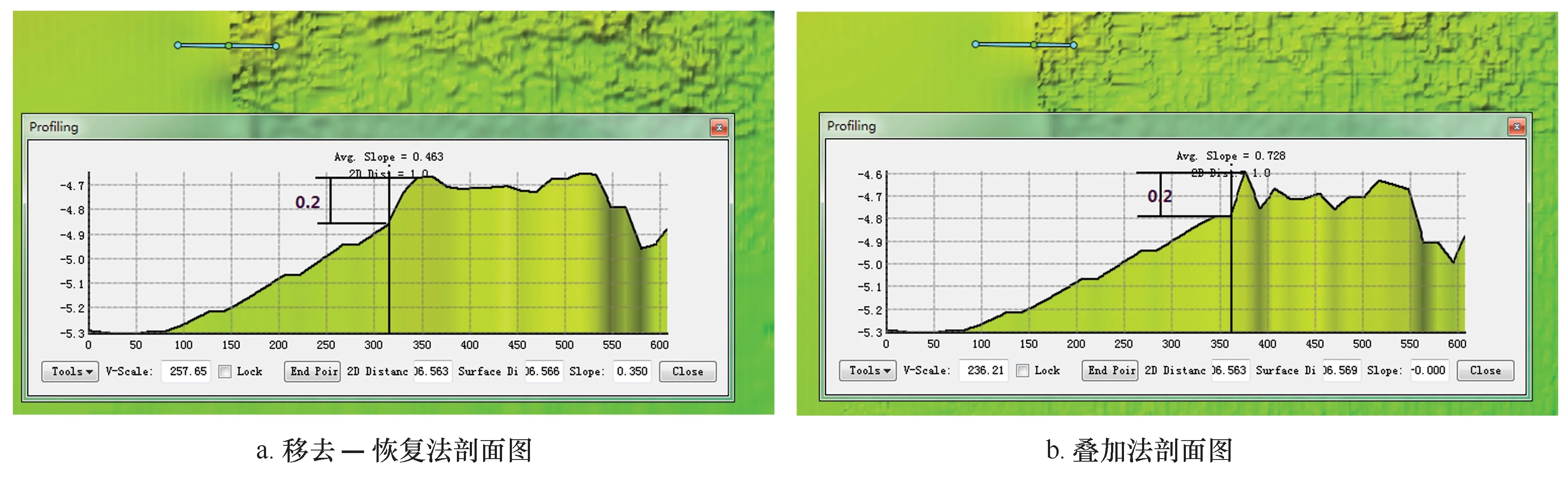
图6 接边处剖面对比Fig.6 Profile comparison to stacked splines grid at transition area

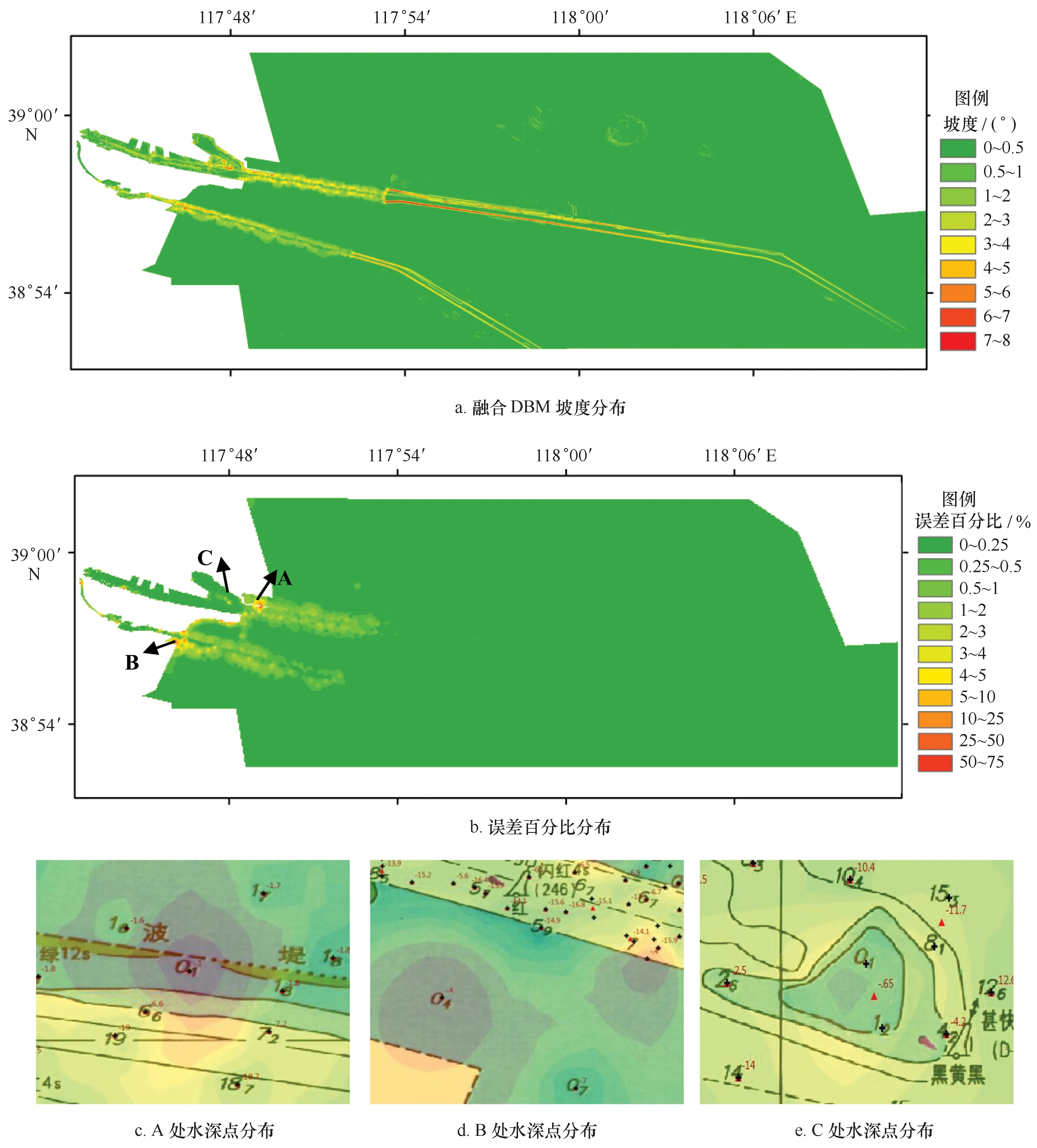
图7 Split-sample方法水深不确定性评估结果及分析Fig.7 The result of split-sample methodology and overlap analysis

4 结论

上述融合方法，利用多源数据，实现了已有数据区和数据空白区间的数据融合，本文所选区域为近岸平坦海域，可以看出生成的海底DBM较好地反映了真实的海底地形，在数据稀疏区，生成的海底地形光滑，在数据密度较大的区域保留了高精度数据更多的细节信息；该方法同样适合于海底地形变化剧烈区，Jakobsson等和Arndt等利用该方法完成了南北极海底地形融合[11—12]取得了很好的效果。本文还对融合方法的不确定性进行了定性和定量评估，可以看出在融合结果中，整体精度较高，只是在浅水数据稀疏区域且地形坡度相对较大的地区水深不确定性大，因此在地形较复杂的地区应尽可能保证高精度、高密度的测量结果，可对融合结果产生决定性改善。总之，基于“移去-恢复” 法的高精度海底地形重建，能够形成可靠的海底DBM，为近岸海洋灾害风险预警，生态保护以及开发管理和利用等提供数据基础。同样本方法在以下方面还需改进：

(1)采用张力样条插值方法，张力因子的设置比较随意，张力因子与格网分辨率及所选地形有关，在进行该方法应用中，应着重考虑上述两个因素，适当选择最佳参数。本文在试验过程中，从0～0.75每隔0.1取值进行计算，发现同一地形，不同分辨率所选的张力因子有所差异，本文在网格插值中，张力因子运用0.3，插值效果及各项误差统计参数为最小。

(2)该方法在数据接边处，尤其是分辨率差异较大的地方还要寻求其他的方法对其进行改进；

(3)同比其他插值方法，张力样条法进行插值时需要耗费较大的内存和时间，因此数据量大时，应根据插值网格大小和插值范围适当进行分块处理。

[1] Sandwell D, Smith W H F. Bathymetric Estimation[M]//Fu L L, Cazenave A. Satellite Altimetry and Earth Sciences: A Handbook of Techniques and Applications. San Diego, CA: Academic Press, 2001: 441-457.

[2] Becker J J, Sandwell D T, Smith W H F, et al. Global bathymetry and elevation data at 30 arc seconds resolution: srtm30_plus[J]. Marine Geodesy, 2009, 32(4): 355-371.

[3] Jakobsson M, Calder B, Mayer L. On the effect of random errors in gridded bathymetric compilations[J]. Journal of Geophysical Research, 2002, 107(B12): ETG 14-1-ETG 14-11.

[4] Elmore P A, Steed C A. Algorithm design study for bathymetry fusion-review of current state-of-the-art and recommended design approach[R]. San Diego, CA: Naval Research Laboratory, Marine Geosciences Division, 2008

[5] Gesch D, Wilson R. Development of a seamless multisource topographic/bathymetric elevation model of tampa bay[J]. Marine Technology Society Journal, 2002, 35(4): 58-64.

[7] Jha S K, Bailey B, Minsker B S, et al. Updating river bathymetry with multiple data sources using kriging[C]//American Geophysical Union, Fall Meeting 2011. Denver, CO: American Geophysical Union, 2011: 1329.

[8] Carter G S, Shankar U. Creating rectangular bathymetry grids for environmental numerical modelling of gravel-bed rivers[J]. Applied Mathematical Modelling, 1997, 21(11): 699-708.

[9] Hell B, Jakobsson M. Gridding heterogeneous bathymetric data sets with stacked continuous curvature splines in tension[J]. Marine Geophysical Research, 2011, 32(4): 493-501.

[10] Sindhu B, Suresh I, Unnikrishnan A S, et al. Improved bathymetric datasets for the shallow water regions in the Indian Ocean[J]. Journal of Earth System Science, 2007, 116(3): 261-274.

[11] Jakobsson M, Mayer L, Coakley B, et al. The international bathymetric chart of the Arctic Ocean (IBCAO) Version 3.0[J]. Geophysical Research Letters, 2012, 39(12): L12609.

[12] Arndt J E, Schenke H W, Jakobsson M， et al. The International Bathymetric Chart of the Southern Ocean (IBCSO) Version 1.0-a new bathymetric compilation covering circum-antarctic waters[J]. Geophysical Research Letters, 2013, 40(12): 3111-3117.

[13] Jha S K, Mariethoz G, Kelly B F J. Bathymetry fusion using multiple-point geostatistics: novelty and challenges in representing non-stationary bedforms[J]. Environmental Modelling & Software, 2013, 50: 66-76.

[14] Smith W H F, Sandwell D T. Global sea floor topography from satellite altimetry and ship depth soundings[J]. Science, 1997, 277(5334): 1956-1962.

[15] Smith W H F, Wessel P. Gridding with continuous curvature splines in tension[J]. Geophysics, 1990, 55(3): 293-305.

[16] Jakobsson M, Macnab R，Mayer L, et al. An improved bathymetric portrayal of the Arctic Ocean: implications for ocean modeling and geological, geophysical and oceanographic analyses[J]. Geophysical Research Letters, 2008, 35(7): L07602.

[17] Forsberg R, Tscherning C C. The use of height data in gravity field approximation by collocation[J]. Journal of Geophysical Research: Solid Earth, 1981, 86(B9): 7843-7854.

[18] Calder B. On the uncertainty of archive hydrographic data sets[J]. IEEE Journal of Oceanic Engineering, 2006, 31(2): 249-265.

[19] 王耀革. DEM建模与不确定性分析[D]. 郑州: 解放军信息工程大学, 2009: 21-32.

Wang Yaoge. Study of DEM generation and uncertainty[D]. Zhengzhou: PLA Information Engineering University, 2009: 21-32.

[20] Hare R, Eakins B, Amante C. Modelling bathymetric uncertainty[J]. International Hydrographic Review, 2011, 4(2): 31-42.

[21] International Hydrographic Organization, Intergovernmental Oceanographic Commission.IOC Manuals and Guides 63[S].Monaco:IHO Publication B-11,2015:429.

[22] 刘艳霞, 黄海军, 杨晓阳. 基于遥感反演的莱州湾悬沙分布及其沉积动力分析[J]. 海洋学报, 2013, 35(6): 43-53.

Liu Yanxia, Huang Haijun, Yang Xiaoyang. The transportation and deposition of suspended sediment and its dynamic mechanism analysis based on Landsat images in the Laizhou Bay[J].Haiyang Xuebao, 2013, 35(6): 43-53.

Bathymetry fusion techniques for high-resolution digital bathymetric modeling

Fan Miao1, Sun Yi1, Xing Zhe1，Wang Yiting1, Li Sihai1, Jin Jiye1

(1.NationalMarineDataandInformationService,Tianjin300171,China)

This paper reviews current fusion techniques used for bathymetry data, introduces the “Splines-in-Tension” interpolation and “remove-restore” techniques for bathymetry fusion. Based on these techniques, high-resolution digital bathymetric model is built using multi-beam, single-beam and historical charts data sets. In addition, facing the lack of error estimates for the interpolated grid points, the paper uses split-sample method to assess the uncertainty of the result for reliability. It shows a satisfied result with error percent about 0.5% both in sparse and dense areas, preserving the detail information of high-resolution data, possessing the vivid characteristics of the sea bottom. The whole techniques can be applied in multi-sources data fusion and combination.

multi-beam; bathymetry fusion; Splines-in-Tension interpolation; split-sample

10.3969/j.issn.0253-4193.2017.01.014

2016-01-29；

2016-08-21。

“全球变化与海气相互作用”专项资助(GASI-01-01-11)。

樊妙(1982—)，女，陕西省商洛市人，高级工程师，主要从事海洋GIS、海底数据处理方法研究。E-mail: fm_nmdis@163.com

P229.1

A

0253-4193(2017)01-0130-08

樊妙，孙毅，邢喆，等. 基于多源水深数据融合的海底高精度地形重建[J]. 海洋学报, 2017, 39(1): 130-137,

Fan Miao, Sun Yi, Xing Zhe, et al. Bathymetry fusion techniques for high-resolution digital bathymetric modeling[J]. Haiyang Xuebao, 2017, 39(1): 130-137, doi: 10.3969/j.issn.0253-4193.2017.01.014