电磁轴承支承特性的主动可控性研究

王 骏，蒋科坚，徐 骏

(浙江理工大学信息学院，杭州 310018)

电磁轴承支承特性的主动可控性研究

王 骏，蒋科坚，徐 骏

(浙江理工大学信息学院，杭州 310018)

以PID控制的主动电磁轴承系统为基础，给出了电磁轴承支承特性理论表达式的参数构成，分析了比例、积分、微分控制参数和控制时滞对电磁轴承支承特性的影响，并通过针对性的实验，对电磁轴承支承特性的可控性及控制关系进行定量分析。实验结果表明：控制时滞决定了电磁轴承的支承特性是否与激振频率有关；控制算法中的积分项主要影响低频区等效阻尼的正负，对等效刚度的影响基本可以忽略；系统的固有频率和差动结构会使电磁轴承的等效刚度和等效阻尼值有所减小。

电磁轴承；支承特性；可控性；控制参数

0 引 言

主动电磁轴承(active magnetic bearing, AMB)，也称电磁轴承，是一种利用电磁力将转子无接触悬浮支承的新型机电一体化轴承，具有无摩擦、无需润滑等优良特性，适用高速场合，可实现转子振动主动控制。因此，它在高速旋转机械设计中越来越受重视，并已在涡轮分子泵、透平压缩机、飞轮储能等工业领域成功实现了产业化应用[1-3]。

在转子动力学中，通常采用刚度和阻尼来描述机械轴承的支承特性。为了能借鉴传统机械轴承的研究理论和分析方法，在电磁轴承领域中引用等效刚度和等效阻尼的概念。电磁轴承的支承特性不仅与其结构尺寸有关，而且在很大程度上取决于其控制系统，即在电磁轴承的尺寸结构一定时，可以通过控制系统在一定范围内调节其刚度、阻尼以及支承的稳定性。因此，电磁轴承的支承特性是设计高性能的轴承系统的重要内容。目前，对电磁轴承支承特性的研究已有较多成果。Tsai等[4]提出了一种利用小波变换算法识别主动电磁轴承的刚度和阻尼的方法。Amer等[5]对电磁轴承转子的共振行为与时变刚度的关系进行了研究，并分析了系统参数对转子非线性响应的影响。Hegazy等[6]介绍了一种在参数激励下具有时变刚度的电磁轴承转子系统，并利用频率响应函数的方法从理论上分析了电磁轴承在共振情况下各种参数对系统稳态响应和稳定性的影响。汪希平[7]分析了电磁轴承的刚度阻尼特性与系统结构参数及其控制器频响特性之间的关系。刘明尧等[8]研究了主动磁力轴承转子系统的非线性支承特性，揭示了控制参数和结构参数与支承特性的耦合关系。谢振宇等[9]研究了零偏置电流电磁轴承转子系统的动态性能，并与有偏置电流方式进行了详细对比。Tang等[10]研究了主动和被动混合电磁轴承控制力矩陀螺转子的动态特性，分析了模态频率与刚度阻尼之间的关系。肖凯等[11]研究了系统的动刚度、动阻尼特性，并从频域的角度分析了PD控制器参数与系统刚度阻尼的关系。丁鸿昌等[12]分析了高速电机永磁偏置混合磁轴承的结构和工作原理，并结合PD控制器参数仿真分析了磁轴承的刚度阻尼特性。

在电磁轴承支承特性研究中，往往为了简化分析而直接用PD控制进行电磁轴承刚度阻尼的理论推导，或者忽略系统控制时滞。然而，实际的电磁轴承很少使用纯粹的PD控制，且必然存在控制时滞，忽略积分和忽略控制时滞都不符合实际情况，分析结果会有较大误差。本文分析了比例、积分、微分控制参数和控制时滞对电磁轴承支承特性的影响和控制关系，并对电磁轴承支承特性的可控性实现定量分析和实验验证。

1 电磁轴承工作原理和支承特性分析

1.1 电磁轴承基本结构及数学模型

电磁轴承主要由控制器、位移传感器、功率放大器、转子轴颈和定子等组成，其基本结构如图1所示。转子悬浮在按径向正交对称放置的定子电磁铁所产生的磁场中。位移传感器可以监测转子的位置变化。当转子偏离期望位置后，位移传感器把位移信号反馈给控制器，控制器产生控制信号，经过功率放大器放大，驱动电磁铁绕组调节磁场，从而改变电磁力，实时修正转子的位置偏差，维持转子稳定悬浮在期望位置，并达到一定的悬浮精度要求。

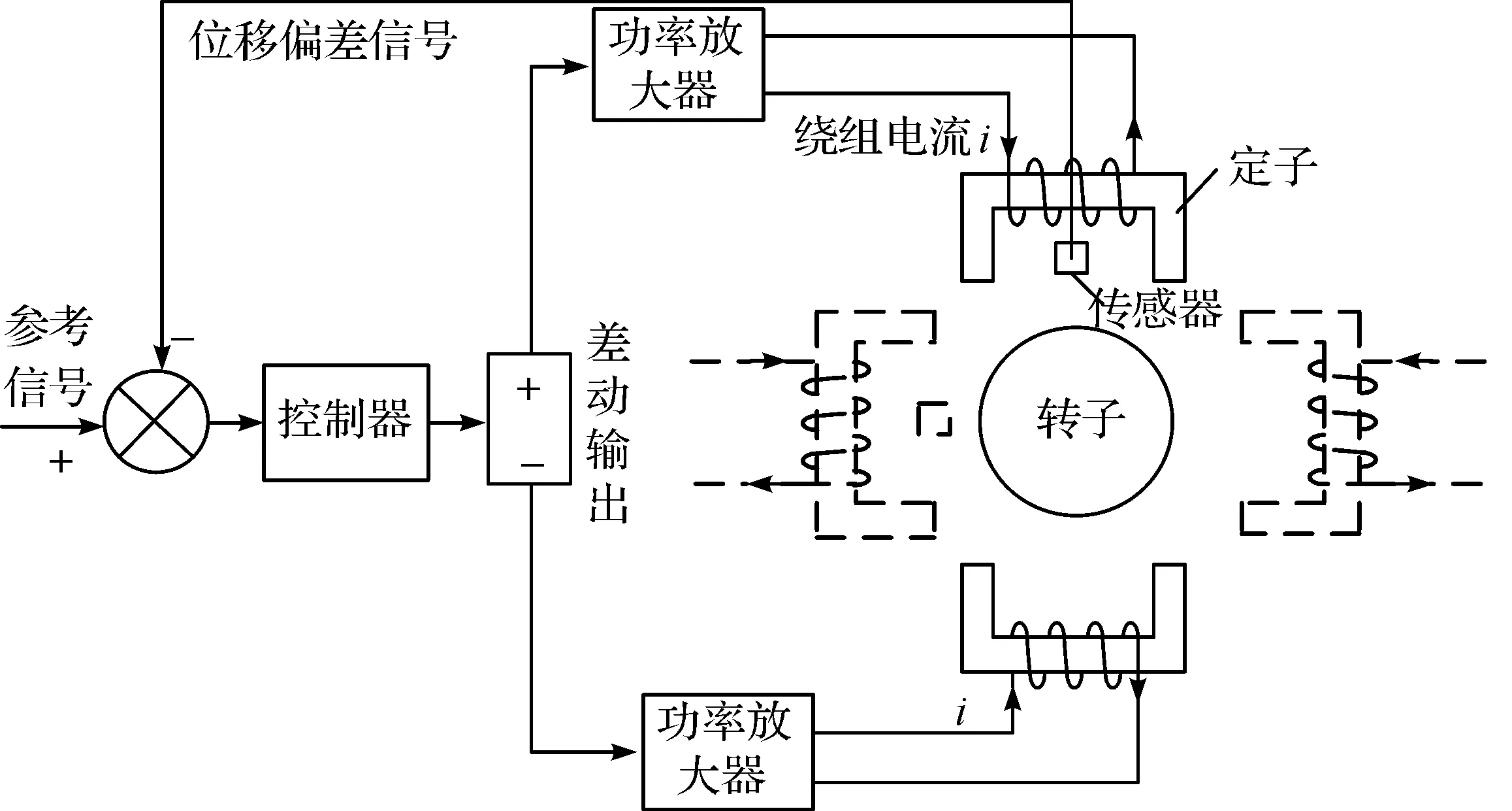
图1 电磁轴承系统基本结构框图

单自由度的电磁轴承系统数学控制模型可表示成图2。其中，m为转子质量，s为拉普拉斯复变量，P(s)为作用于转子上的外界干扰力，转子位移信号X(s)由位移传感器检测出，与给定的参考位置Xref相减得出位移偏差信号并传递给控制系统，Gc(s)是控制器的传递函数，输出控制信号经放大倍数为Kw的功率放大器，输出对应的控制电流I(s)，使电磁铁产生电磁力F(s)。电磁轴承的电磁力由电流刚度系数Ki和位移刚度系数Kx表示。电磁力F(s)和外界干扰力P(s)共同作用于转子，形成转子动力学运动。

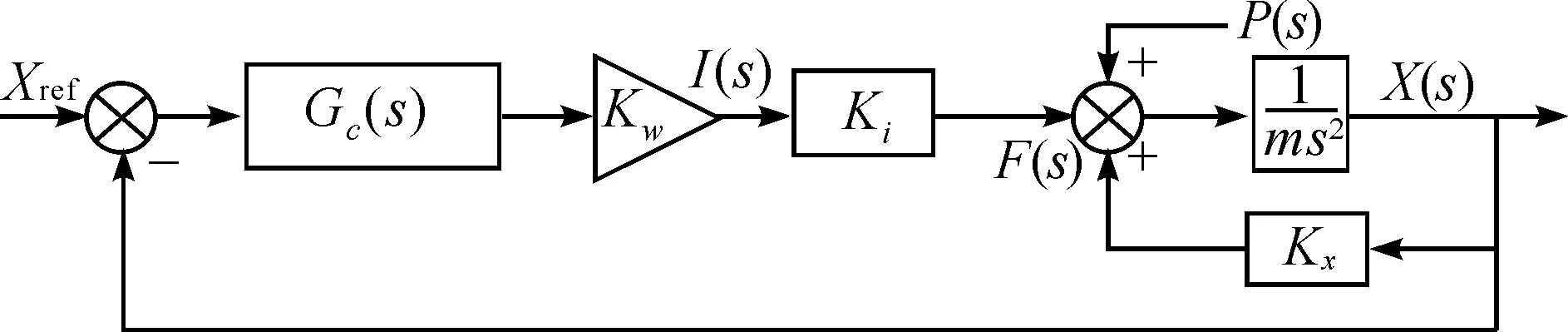
图2 单自由度电磁悬浮系统控制框图

1.2 等效刚度和等效阻尼的理论分析

1.2.1 等效刚度和等效阻尼的理论计算

把电磁轴承的单自由度悬浮运动方程与传统质量-弹簧-阻尼结构的运动方程进行比较，可以得出电磁轴承等效刚度Ke和等效阻尼Ce的一般表达式[7,13-15]：

Ke=KiRe[G(jω)]-Kx

(1)

(2)

其中：G(jω)为主动电磁轴承整个控制系统的传递函数，通常包括控制器、位移传感器、功率放大器开环传递函数的总和。Re[G(jω)]为G(jω)的实部，Im[G(jω)]为G(jω)的虚部，Ki为电流刚度系数，Kx为位移刚度系数。

设功率放大器的放大倍数为Kw，位移传感器转换倍率为Kc，系统的整体控制时滞为T，PID控制参数比例、积分和微分系数分别为kp、ki、kd，那么整个控制系统的传递函数可表示为：

(3)

将式(3)的频域方程形式代入式(1)和式(2)，可得PID控制下的电磁轴承等效刚度和等效阻尼的表达式：

(4)

(5)

1.2.2 控制时滞对电磁轴承支承特性的影响

在0～6 ms内取间隔为1 ms的7个控制时滞值进行仿真计算，将实验参数值代入式(4)和式(5)。其中已知电磁轴承功率放大器的放大系数Kw=2 A/V，位移传感器以及调理电路总的放大系数Kc=9440 V/m，位移刚度系数Kx=0.24 MN/m，电流刚度系数Ki=125 N/A，频率测试范围为1～600 Hz。为了避免积分环节的影响混杂在分析数据中，单纯采用PD控制，得到的结果如图3和图4所示。

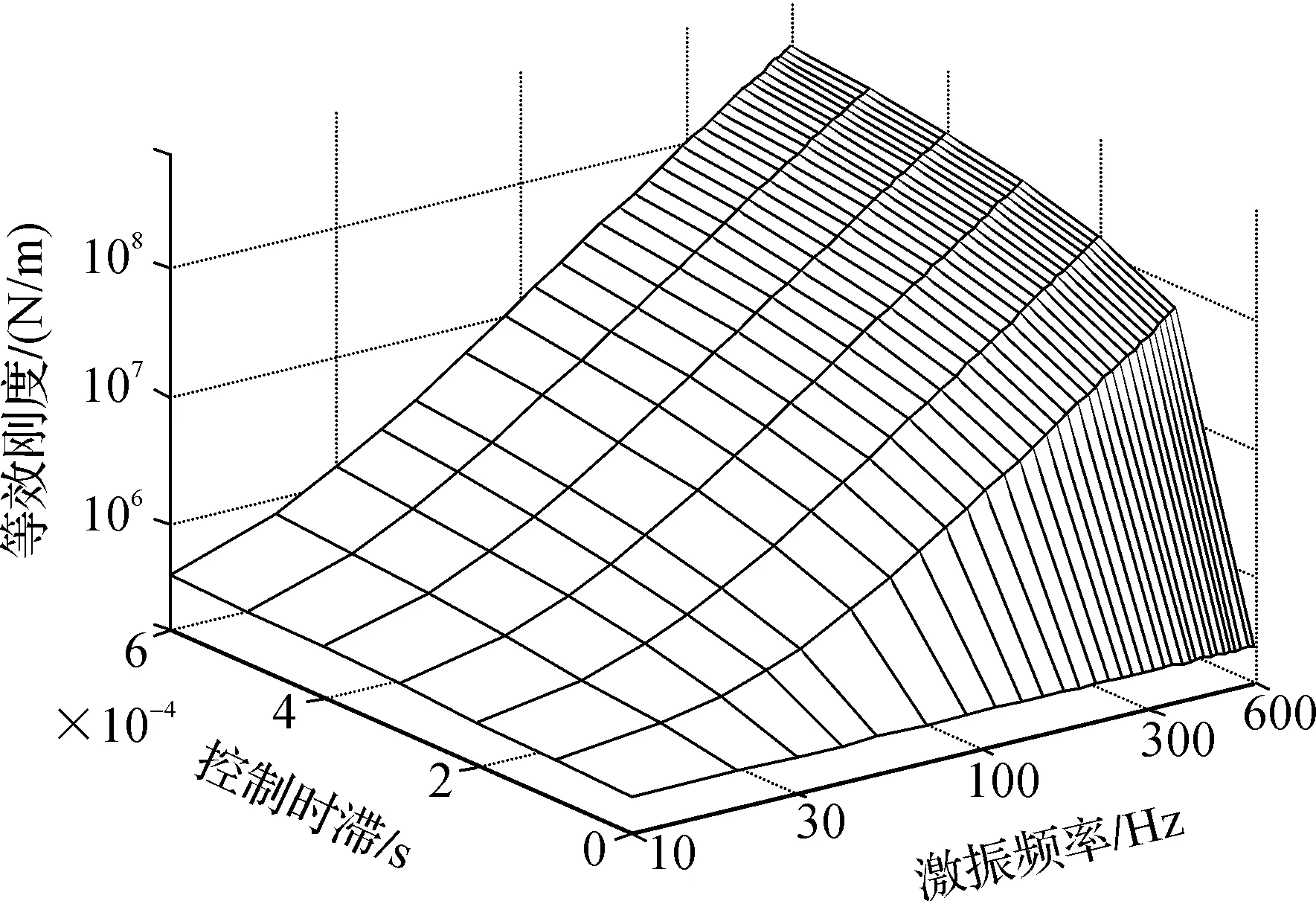
图3 控制时滞T对等效刚度的影响

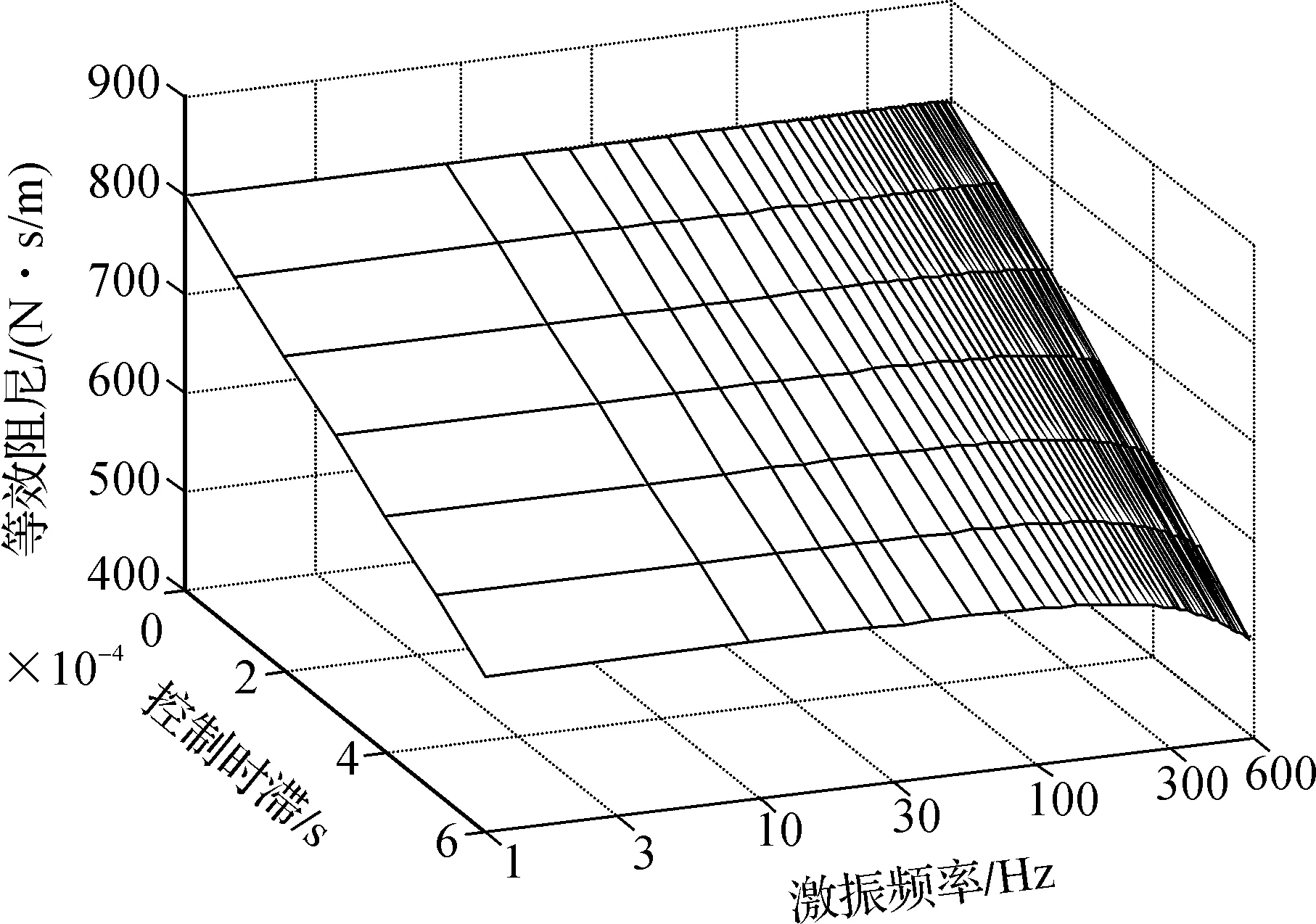
图4 控制时滞T对等效阻尼的影响

结合式(4)和图3可知，控制时滞为0时，等效刚度始终为定值，并不随频率而变化，其值只由控制参数中的比例系数kp决定。随着控制时滞的增大，等效刚度值随频率上升的越快。

由图4可以看出，控制时滞为0时，等效阻尼始终为定值，不随频率而变化，分析式(5)可知，此时其值只由微分系数kd决定。当控制时滞不为0时，等效阻尼随频率而变化。随着控制时滞的增大，同一频率下，等效阻尼值逐渐减小。同时可以看到，随着频率的升高，分母1+ω2T2项逐渐增大，使得等效阻尼值在高频区逐渐下降。

1.2.3 考虑时滞情况下PID控制参数对电磁轴承支承特性的影响

电磁轴承支承特性的可控性主要体现在控制参数的可调性。为了研究控制参数各自独立的对电磁轴承支承特性的影响，当研究kp时，取ki为0，kd等于1.5；研究kd时，取ki为0，kp等于0.2；研究ki时，取kp为0.2，kd等于1.5。考虑实际系统，取控制时滞的典型值为T=4×10-4s，将已知参数代入式(4)和式(5)，频率测试范围为1～600 Hz，可得有控制时滞的电磁轴承刚度阻尼特性。

比例系数kp对等效刚度的影响如图5所示，等效刚度的值主要由kp的值决定，kp增加，等效刚度也随之增大。同时，kp一定时，等效刚度也随频率的增大而增大。由于系统延时T很小，由式(5)可知，比例系数kp对等效阻尼的影响非常小，如图6所示。随着频率的升高，分母1+ω2T2项逐渐增大，等效阻尼有明显下降。

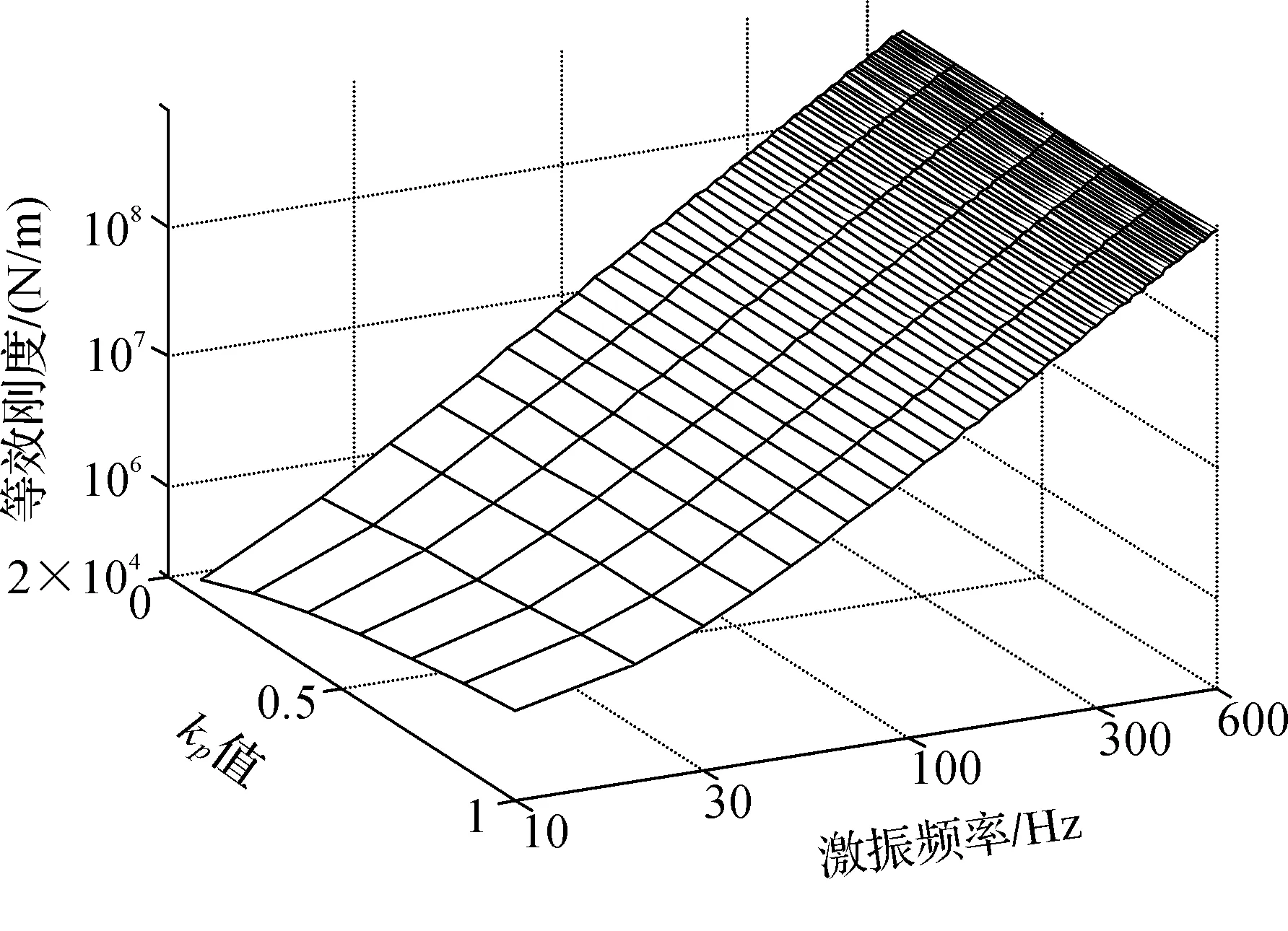
图5 比例系数kp对等效刚度的影响

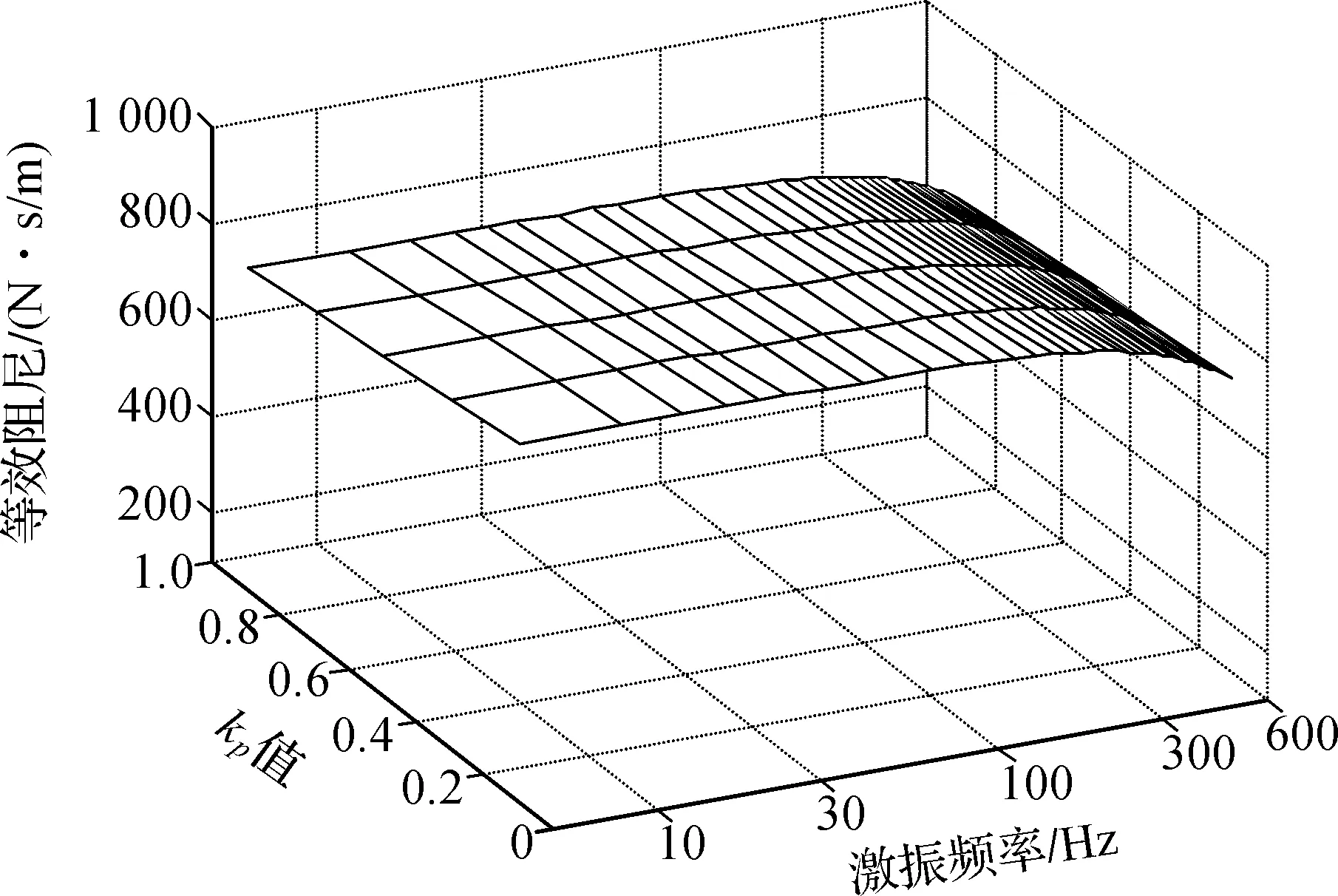
图6 比例系数kp对等效阻尼的影响

kd的值决定了随激振频率的升高等效刚度值上升速度的快慢，kd越大，等效刚度随频率上升的越快，如图7所示。由图8可见，等效阻尼的值主要由kd的值决定，kd增加，等效阻尼也随之增大。同时，kd一定时，等效阻尼随频率升高反而降低。一些文献[7,11-13]也得出了相同的结论。

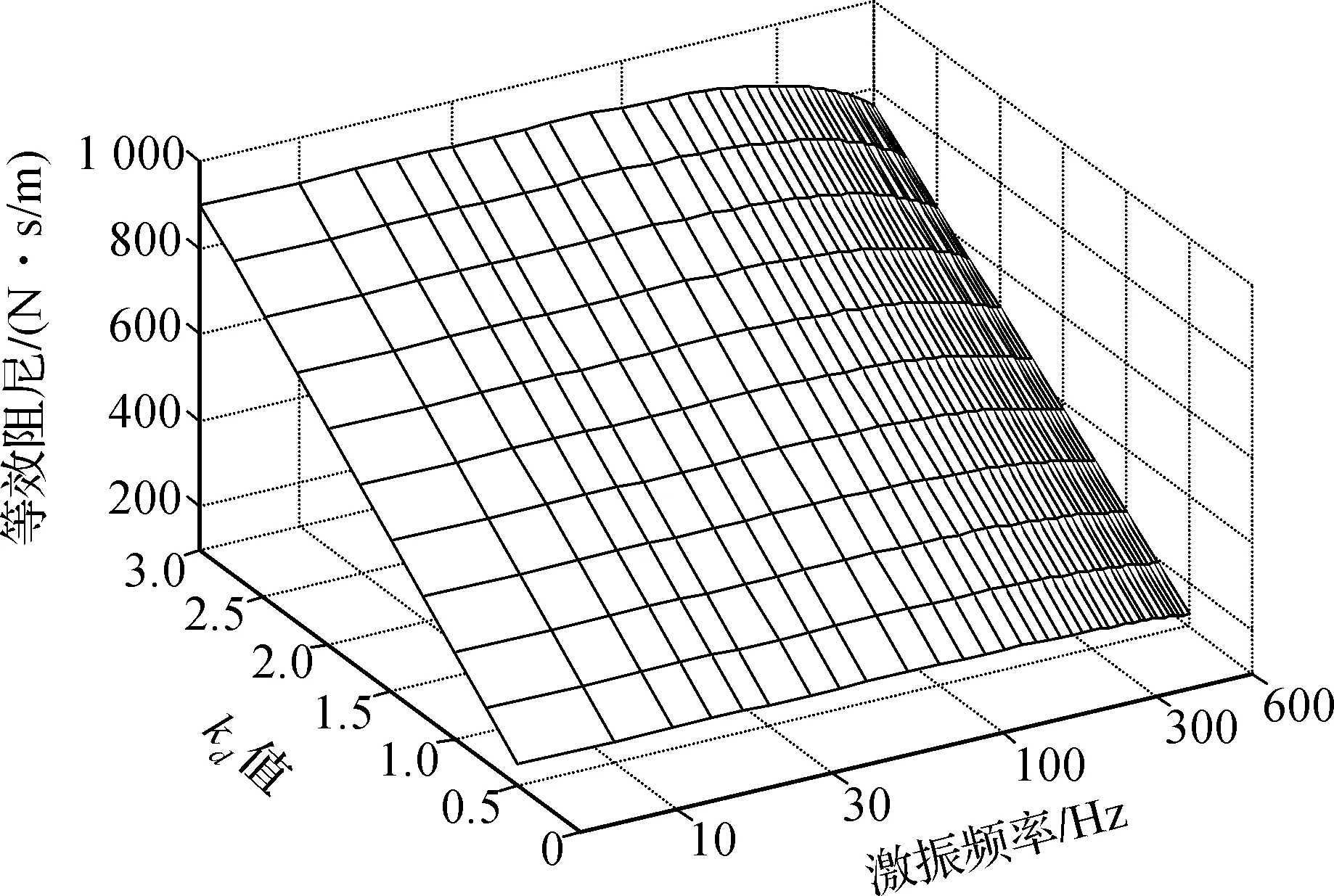
图8 微分系数kd对等效阻尼的影响

积分系数ki对等效刚度的影响如图9所示。根据图9和式(4)可以看出，由于kiT项的值很小，积分系数ki对等效刚度几乎没有影响。图10为积分系数ki的变化与等效阻尼的关系图。积分系数ki对等效阻尼影响较大。对照式(5)，当积分系数ki很小，接近0，和图6、图8一样的情况，等效阻尼在中低频区基本保持不变，比较平直。频率升高以后，分母1+ω2T2项的影响逐渐增大，等效阻尼有明显下降，但整个频率段都为正值。当积分系数ki增大，积分影响增强，由于-ki/ω2项的存在，可以看到在低频区等效阻尼会出现负值，且积分系数ki越大，等效阻尼在低频区跌幅也越大。随着频率的增大，-ki/ω2的影响逐渐减小，等效阻尼会逐渐升高。随着频率继续增大，分母1+ω2T2项的影响逐渐显现，在高频区等效阻尼的值又会下降，并在中频区形成一个弧顶。

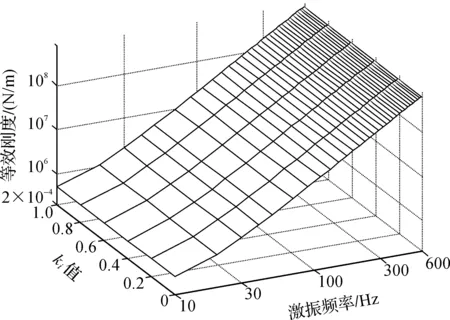
图9 积分系数ki对等效刚度的影响

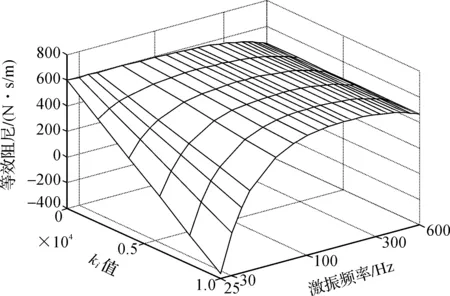
图10 积分系数ki对等效阻尼的影响

2 实验与结果分析

2.1 实验平台

单自由度电磁轴承系统实验平台照片如图11所示。实验平台采用单端悬浮铰支梁结构。悬浮梁一端和铰链相连，另一端由上下两个线圈绕组组成的主动电磁悬浮结构支承，悬浮梁可在较小气隙内实现近似线性悬浮。经过实验测量，悬浮梁的等效质量m=5.8 kg，电磁铁上下线圈匝数N=180匝，磁路的横截面积A≈6.54×10-4m2，气隙总长度x0=0.88 mm，偏置电流i0=1.25 A。在实验条件下，计算得位移刚度系数Kx=0.24 MN/m，电流刚度系数Ki=125 N/A。

图11 单自由度电磁悬浮系统实验平台

实验采用PID控制，并确保电磁轴承系统在整个实验过程中始终处于良好的悬浮状态，以保证实验的准确性。为了研究控制参数各自对电磁轴承支承特性的影响关系，控制参数的取值原则基本和理论分析时保持一致。系统施加激励后，通过参数识别得到等效刚度和等效阻尼值，具体识别方法参见文献[13-15]。实验在激振频率为1～600 Hz的范围内进行。

2.2 比例系数对支承特性影响的测试结果

实验取不同kp值，测得等效刚度和等效阻尼值分别如图12-图13所示。由图12可见，等效刚度值随频率的升高而增大，显然实际系统有延时。当处于同一频率时，等效刚度值随比例系数kp的增大而增大，这在低频阶段表现尤为明显。而图13却看不出不同kp下等效阻尼各曲线之间的差异，整个频率域中等效阻尼曲线都相互交织在一起，差异很小，说明kp主要影响等效刚度，对等效阻尼的影响不是很明显，这与理论分析相吻合。

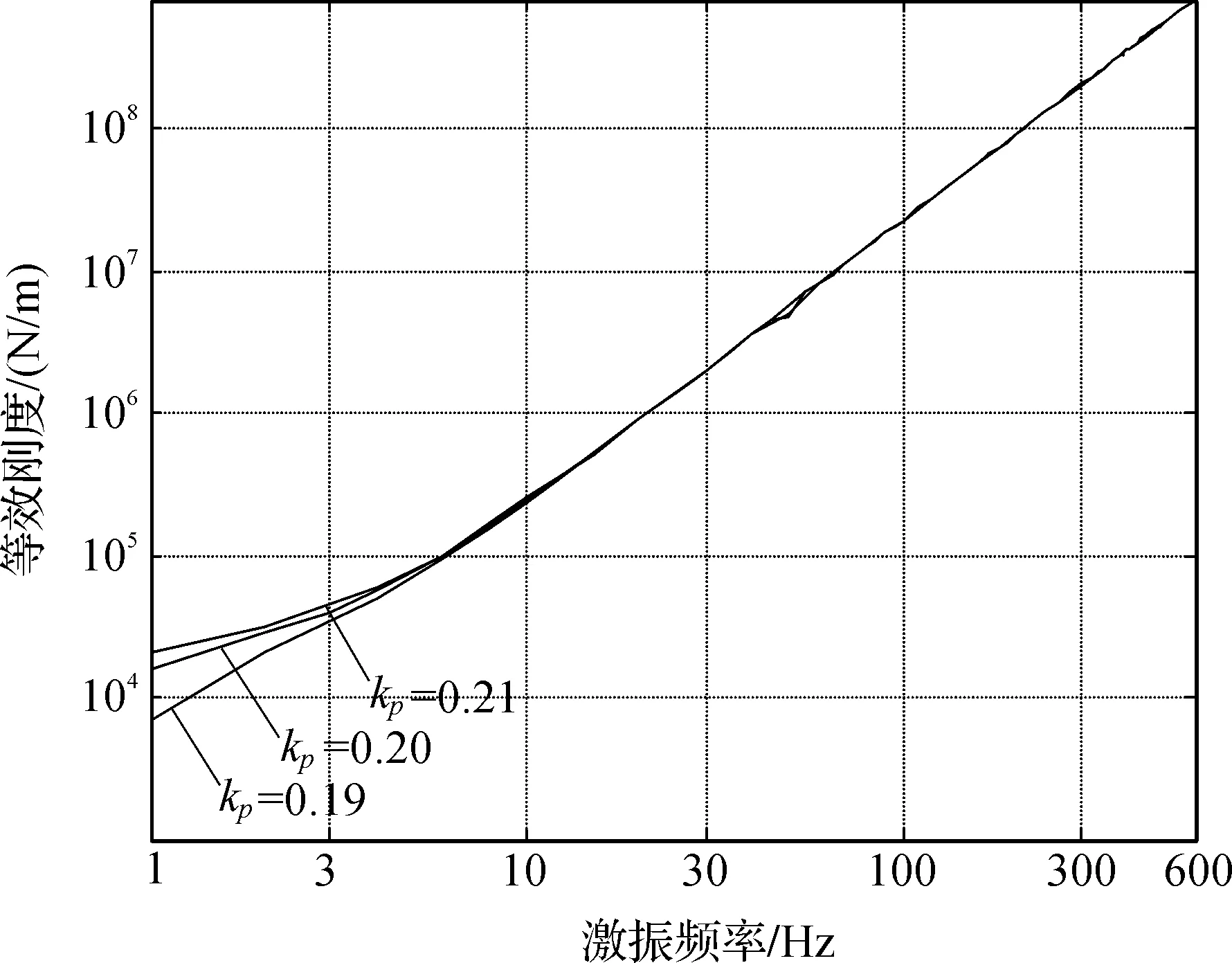
图12 比例系数kp对等效刚度的影响

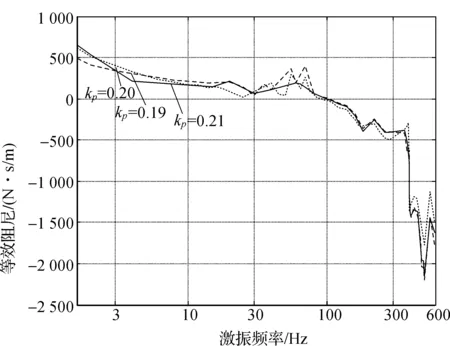
图13 比例系数kp对等效阻尼的影响

2.3 微分系数对支承特性影响的测试结果

由于系统延时T很小，导致不同kd下的等效刚度值差异较小，加之整体等效刚度值较大以及在线测量系统在高频区识别误差的增大，使得kd对等效刚度的影响表现的不是很明显，见图14。由图15可以清楚地看到，微分系数对等效阻尼的影响非常明显。同一频率下，等效阻尼值随kd的增大而增大。

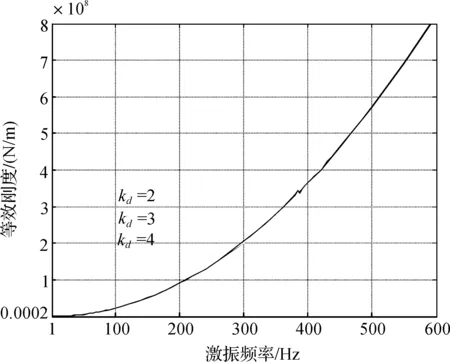
图14 微分系数kd对等效刚度的影响

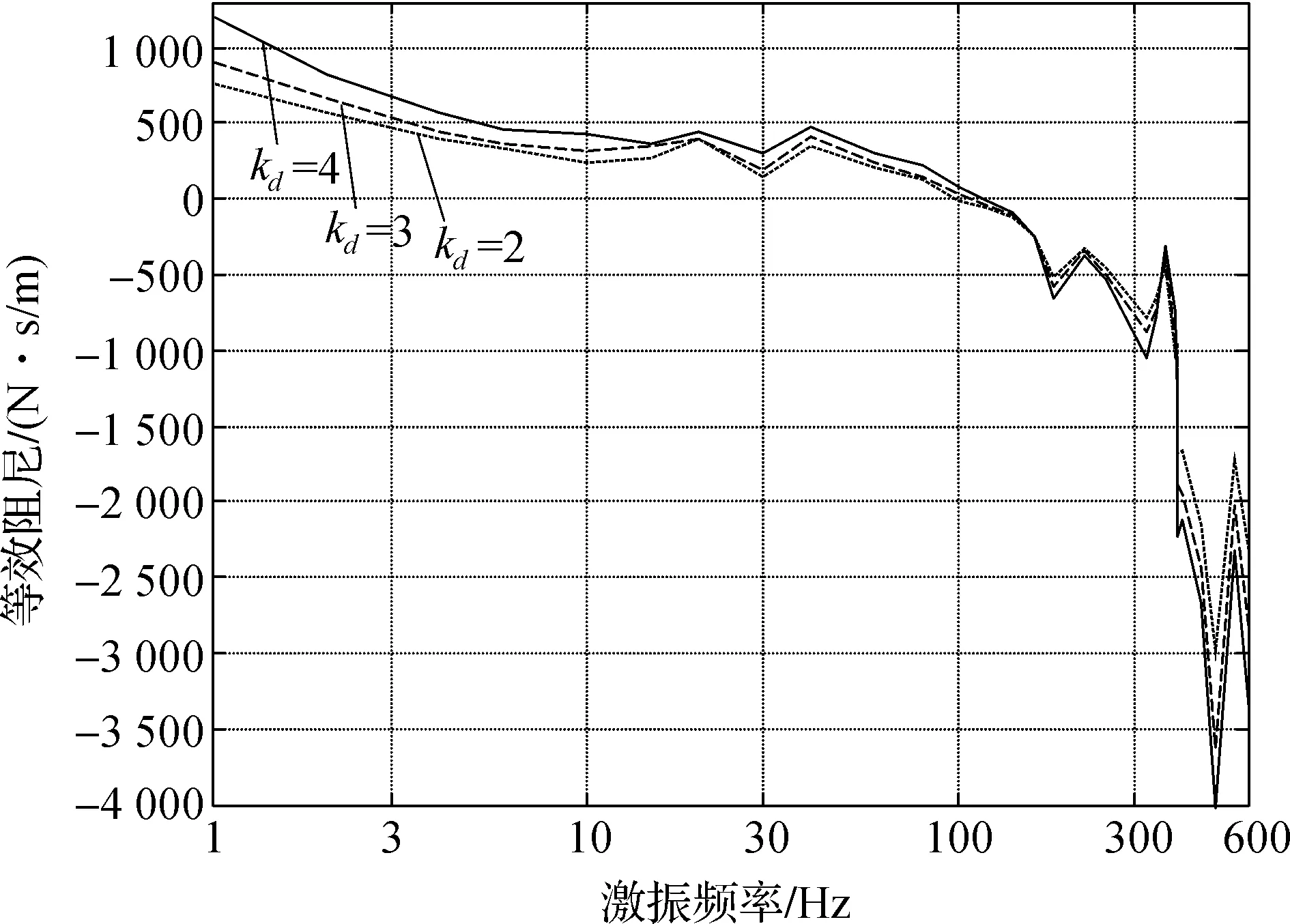
图15 微分系数kd对等效阻尼的影响

2.4 积分系数对支承特性影响的测试结果

由式(4)的等效刚度表达式可知，由于kiT项数量级很小，因此，在整个频率范围内，控制算法中的积分项对等效刚度的影响几乎可以忽略。实验结果如图16所示，对实验台在不同ki条件下，等效刚度值在1～600 Hz范围内的变化情况。图16中多条等效刚度曲线几乎重合，可见积分对等效刚度的影响非常小，这与理论分析一致。

在图16中可以发现，频率在380 Hz左右，等效刚度值有一个小缺口，多次重复实验中始终存在，说明等效刚度在该频率点有下跌，但总体影响不明显。

图16 积分系数ki对等效刚度的影响

实验在线测量不同ki时的等效阻尼值，得到积分系数与等效阻尼的关系如图17所示。由实验结果可以看出，控制算法中的积分控制环节对等效阻尼的低频阶段影响很大。ki值为0时，等效阻尼值在低频区始终为正。反之，低频段等效阻尼出现负值，且ki值越大，等效阻尼往负值坠落幅度越大。这说明积分控制环节对低频段的悬浮稳定性是负面的。这个实验现象与图10的理论分析一致。当激振频率升高后，等效阻尼值会上升，并与积分系数为0时的等效阻尼值重合。这说明积分控制环节的影响在频率升高后逐渐减弱。

图17 积分系数ki对等效阻尼的影响

在图17中可以清楚地看到，频率在380 Hz左右等效阻尼值同样出现明显的下跌，实测等效阻尼值比理论值小很多。随着频率的增大，等效阻尼渐渐恢复到理论值水平，形成“V”字形。这是理论分析没有的现象。

2.5 380 Hz出现刚度阻尼下降的原因

在实验中发现，等效刚度和等效阻尼在频率380 Hz左右都出现了下跌，尤其是等效阻尼影响较大。同时实验中明显感觉，当激振频率在380 Hz附近时，悬浮梁振动幅度明显变大，频率升高后，振动又有好转。从现象看，实验台在380 Hz频率点有一个共振点。

进一步分析，由于实验台上下线圈的控制系统采用差动结构，即流经上下两个线圈的电流一个为偏置电流与控制电流之和，另一个为偏置电流与控制电流之差。因此，当悬浮振动幅度较大时，可能使得控制电流大于偏置电流，造成一侧线圈电流理论上会成为负值，实际中把负值电流处理成电流为零。其造成的结果是当控制电流大于偏置电流时，电磁力仅由单侧线圈提供，从而导致等效刚度和等效阻尼值的下降。另外，大电流引起电磁力饱和也是等效刚度和等效阻尼值下降的原因。

为了证明上述分析，进行下面实验。通过增大激振力振幅，从而加大电磁轴承振动的幅度，使得控制电流变化峰值超过偏置电流，必将会有一侧线圈不能持续提供电磁力。大振幅和小振幅激振力作用下系统输出控制电流的变化示意图如图18所示，转子位移信号实时波形图如图19所示。

图18 不同振幅激振力作用下控制电流变化

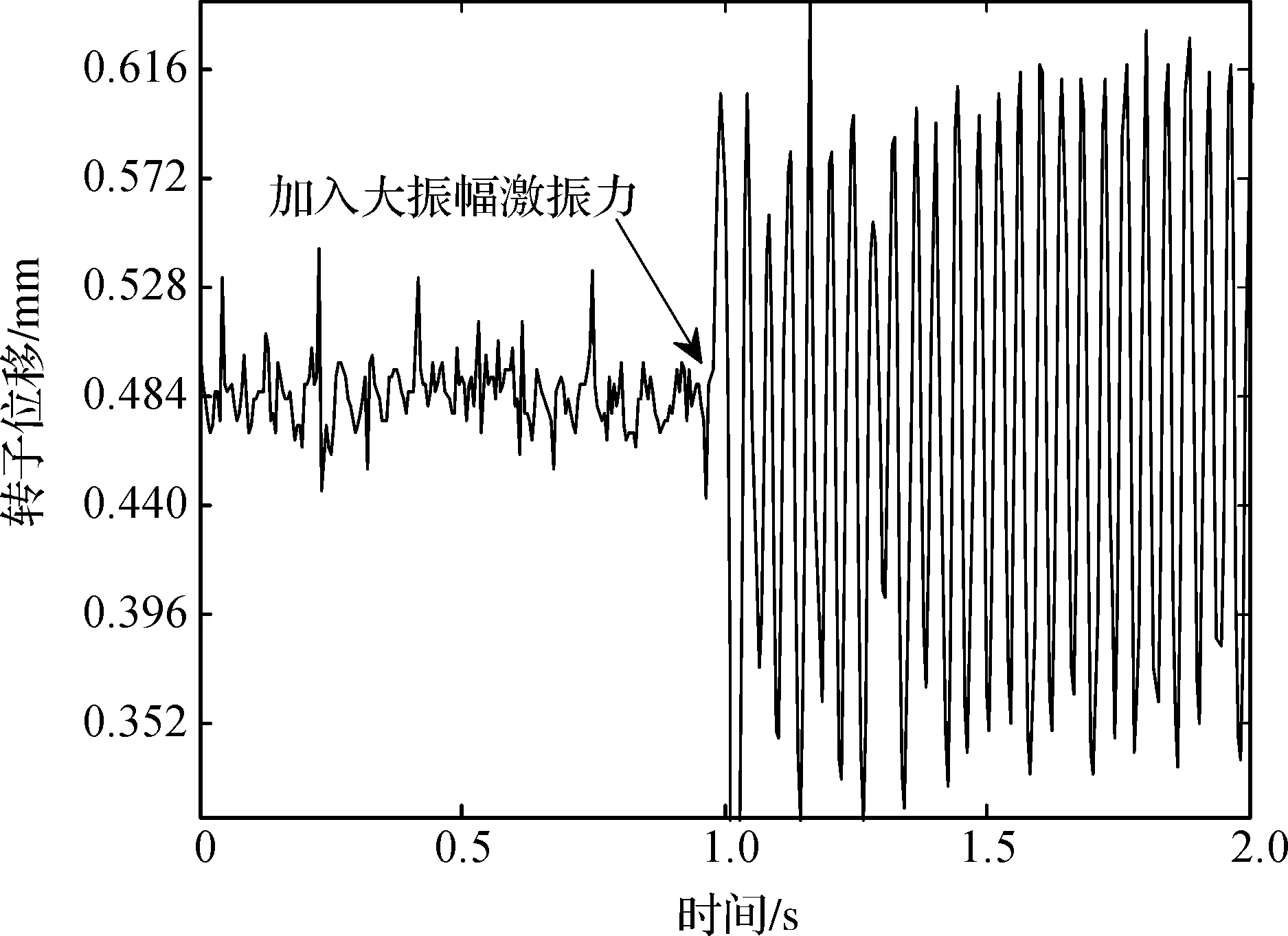
图19 转子位移信号实时波形图

从图18中可以看到，偏置电流数字量为300(换算成电流值为0.68 A)。当在较小振幅激振力作用下，控制电流变化范围始终稳定在-300～300之间，始终小于偏置电流。在这个范围内，上下线圈均能提供持续的电磁力。

当施加较大振幅激振力时，系统输出的控制电流显然有很大一部分超出了-300～300的范围。此时，超出时刻的电磁力只由一侧线圈产生。这种情况在偏置电流较小时，尤为明显。

实验选择激振频率为100 Hz，施以12N和104N两种大小不同的激励，比较等效刚度和等效阻尼的测量值变化。结果如表1所示。由此可以看出，即使不在共振频率，只要加大激励振幅，就会导致系统的等效刚度和等效阻尼值明显的下降。

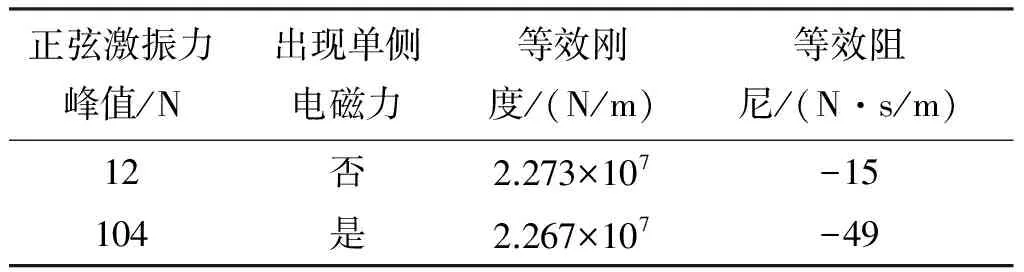
表1 大小激振力对等效刚度和等效阻尼值的影响

3 结 论

本文对电磁轴承系统支承特性的主动可控性进行了理论分析和实验研究，主要结论如下：

a)当不考虑积分和控制时滞时，电磁轴承的等效刚度和等效阻尼都为常数，不随频率变化。比例系数决定电磁轴承的等效刚度，微分系数决定电磁轴承的等效阻尼。

b)当考虑控制时滞作用时，等效刚度随频率逐渐升高；等效阻尼在中低频还能基本保持常数，但到高频时，会由于控制时滞作用而下降。

c)积分环节对电磁轴承的等效刚度影响不明显，主要影响等效阻尼，而且是等效阻尼的低频段。当采用纯粹的PD控制，低频区的等效阻尼始终为正值。加入积分环节后，使等效阻尼在低频阶段明显下降，积分越大，等效阻尼值下降越多，可以下降到负值。

d)由于电磁轴承上下线圈采用差动结构，使得在系统共振或振幅较大时，出现控制电流大于偏置电流，导致电磁力只由一侧线圈提供，会引起等效刚度和等效阻尼值下降，对等效阻尼的影响尤为明显。

实验结果反映了实际系统中电磁轴承等效刚度和等效阻尼的变化特性，其结论可以为电磁轴承系统的设计提供依据。

[1]EATON D, RAMA J, SINGHAL S. Magnetic bearing applications & economics[C]// Petroleum and Chemical Industry Conference (PCIC). 2010 Record of Conference Papers Industry Applications Society 57th Annual. San Antonio：IEEE,2010:1-9.

[2]JANG H D, KIM J, HAN D C, et al. Improvement of high speed stability of an aerostatic bearing-rotor system using an active magnetic bearing[J]. International Journal of Precision Engineering and Manufacturing,2014,15(12)：2565-2572.

[3]XIANG M, WEI T. Autobalancing of high-speed rotors suspended by magnetic bearings using LMS adaptive feedforward compensation[J]. Journal of Vibration & Control,2013,20(9):1428-1436.

[4]TSAI N C, LI H Y, LIN C C, et al. Magnetic damping and stiffness effects on rod translation by active magnetic bearing[J]. ARCHIVE Proceedings of the Institution of Mechanical Engineers, Part C：Journal of Mechanical Engineering Science,2011,225(8):1950-1962.

[5]AMER Y A, HEGAZY U H. Resonance behavior of a rotor-active magnetic bearing with time-varying stiffness[J]. Chaos Solitons & Fractals,2007,34(4):1328-1345.

[6]HEGAZY U H, AMER Y A. A time-varying stiffness rotor-active magnetic bearings system under parametric excitation[J]. Proceedings of the Institution of Mechanical Engineers Part C：Journal of Mechanical Engineering Science,2008,222(3)：447-458.

[7]汪希平.电磁轴承系统的刚度阻尼特性分析[J].应用力学学报,1997,14(3):95-100.

[8]刘明尧,胡业发,周祖德,等.磁力轴承转子系统非线性支承特性的研究[J].中国机械工程,2005(15):1377-1379.

[9]谢振宇,龙亚文,徐欣.零偏置电流磁轴承转子系统动态性能的试验研究[J].机械工程学报,2013,49(15):68-73.

[10]TANG J, XIANG B, ZHANG Y. Dynamic characteristics of the rotor in a magnetically suspended control moment gyroscope with active magnetic bearing and passive magnetic bearing[J]. Isa Transactions,2014,53(4):1357-1365.

[11]肖凯,张育林,刘昆.基于PD控制的磁轴承刚度与阻尼分析[J].机床与液压,2007,35(8):26-28.

[12]丁鸿昌,肖林京,陈毕胜.永磁偏置混合磁轴承刚度与阻尼特性研究[J].制造业自动化,2011,33(12):73-75.

[13]蒋科坚,柷长生.未知传递函数情况下主动电磁悬浮系统支承特性在线测量[J].中国机械工程,2010,21(8):883-888.

[14]蒋科坚,柷长生,乔晓利,等.采用多自由度转子模型的电磁轴承支承特性测试方法[J].振动工程学报,2014,23(7):457-465.

[15]JIANG K, ZHU C, CHEN L, et al. Multi-DOF rotor model based measurement of stiffness and damping for active magnetic bearing using multi-frequency excitation[J]. Mechanical Systems & Signal Processing,2015,60/61:358-374.

(责任编辑： 康 锋)

Study on Active Controllability of Supporting Characteristics of Electromagnetic Bearing

WANGJun,JIANGKejian,XUJun

(School of Information Science and Technology, Zhejiang Sci-Tech University, Hangzhou 310018, China)

Based on the active electromagnetic bearing system controlled by PID, this paper gave parameter composition of theoretical expression of supporting characteristics, and analyzed the effects of proportion, integral, differential control parameter and control time-lag on supporting characteristics of electromagnetic bearing. In addition, quantitative analysis was carried out for controllability and control relationship of supporting characteristics. The experimental results show that control time-lag is able to determine whether the supporting characteristics of electromagnetic bearing are related to the excitation frequency; the integral item in the control algorithm mainly affects the plus or minus of equivalent damping in the low frequency area; the effect of equivalent stiffness can be ignored; the natural frequency of the system and the differential structure can make the value of equivalent stiffness and equivalent damping decrease.

electromagnetic bearing; supporting characteristics; controllability; control parameters

10.3969/j.issn.1673-3851.2017.01.013

2016-03-04

日期： 2016-12-09

国家自然科学基金项目(11272288)；浙江省公益技术应用研究项目(2015C31063)；浙江理工大学研究生创新项目(YCX14022)；计算机应用技术浙江省重点学科研究生创新项目(XDY15005)

王 骏(1992-)，男，湖北黄冈人，硕士研究生，主要从事磁悬浮控制方面的研究。

蒋科坚，E-mail：jkjofzju@163.com

TH133

A

1673- 3851 (2017) 01- 0077- 08