初中数学教学中如何应用数形结合思想

姚锦萍

摘 要： 数形结合思想作为数学学习的重要思想之一，在数学学习中发挥着重要作用。教师在初中数学教学过程中要对此思想予以尤其关注和重视，通过多方式让数形结合思想融入学生学习过程中，帮助学生获得更好的学习体验，让学生学习效率得到提升。基于此，本文对初中数学教学中的数形结合思想的应用进行分析研究，并提出相应的策略，期望为教师教学及学生学习提供借鉴。

关键词： 初中数学 数形结合思想 数学能力

引言

随着教育素质的推进，传统教学方式已经无法满足当前的学习需要，正是因为此，初中教学各门学科都在积极研究相应的教改措施，力争让学生学到更实用的知识，将学习的知识更好地应用到生活、学习中。对于初中数学来说同样如此，数形结合思想是数学学习过程中非常重要的思想之一，让学生学习的知识更形象化、生动化，让学生在数学学习大道路上寻找到捷径。因此，教师要对此教学思想予以高度重视，通过相应方式方法，让数形结合思想真正融入学生学习过程中，让学生学习更具有创造性，通过此思想的应用激发学生学习兴趣，提升学生的学习能动性。

一、数形结合思想的认识

数学学习与其他学科不同，更多的是抽象语言应用，容易让学生理解更困难，容易陷入理解的“死循环”中，造成学习的脱节。数形结合思想则是将抽象的语言通过形象化、生动化的图形表现出来，将代数问题转化为几何问题予以解决，从而让难以理解的数学问题变得简单易懂，降低学习难度。数形结合思想是将代数与几何问题有效统一起来，逐渐培养起学生的形象化思维，让学生透过题目表面的阐述深入问题本质中深入理解。

教师在教学过程中可以通过以下几个方面予以把握：首先，建立相应的代数模型，此处所指的模型是方程、不等式或者函数模型，让学生的理解更加深化。其次，建立几何模型解决相关方程或者函数问题，这种方式可以让题目更加形象化。第三，与函数有关的代数、几何综合性模型建设。此种模型的复杂性更强，有助于学生能力提升。第四，通过图形、图像的方式呈现信息的应用性。可以说，数形结合思想贯穿数学学习始终，只有真正将“数”与“形”结合在一起，才能让学生的学习质量和效率得到提高，才能让学生的学习能力得到提升。

二、数形结合思想在初中数学中的应用

1.有理数中数形结合思想的应用

有理数是初中数学学习中的重点，在有理数教学过程中，教师可以将数形结合思想代入其中，让有理数内容成为数形结合思想的有力载体，让学生对有理数的理解更加深刻，让学生的基础学习更加扎实。

比如，笔者在《有理数的运算》教学过程中组织学生进行了一次数学活动，通过活动逐渐渗透数形结合思想。笔者在黑板上绘制一条数轴，将粉笔点在数轴的原点处，先依照数轴正方向移动三个单位的长度，之后“笔锋一转”，再向反方向移动两个单位长度，这时粉笔便停在“1”的位置上。此时，笔者引入有理数的加减法运算，让学生计算3+（-2）=？，这时候同学们不用计算便可以非常形象地看出来，其结果等于“1”。通过形象的方式，学生感受到在粉笔的两次移动过程中点的运动方向和移动距离对应的实际移动效果，“数”和“形”在学生的头脑中产生激烈的碰撞，有理数的运算自然在学生的头脑中形成形象的几何解释。

活动的趣味性将数形结合思想无形之中融入学生的数学学习过程中，让学生在潜移默化中感受到数形结合的重大力量，让学生的学习效率在无形之中得到提高。教师可以探索更有趣的活动让数形结合思想在有理数学习中的渗透更全面而深入。

2.函数学习中数形结合思想的应用

函数学习是初中数学学习中又一大“模块”，对学生后续形成重要的函数思维起到非常重要的作用和影响。但是，函数学习极具抽象性，很多学生在学习函数的过程中遭遇“老大难”，理解起来非常困难，导致很多学生对函数学习丧失信心，进而丧失学习数学的兴趣。而数形结合思想的应用则可以很好地帮助学生学习函数，是数形结合思想的重要表现形式。

比如，笔者在《二次函数》教学过程中给学生设计了这样一个问题：

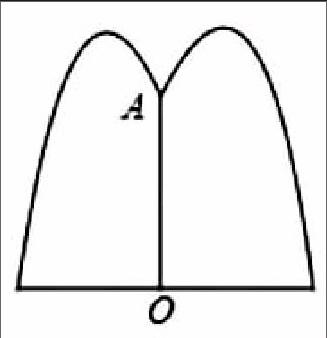
桃核公园要建造圆形喷水池，在水池中央垂直于水面要安装一个柱子，此处我们用OA对其进行表示。O正对水面中心，OA=1.25m。在水柱喷水的时候，水流在各个方向沿形状相同的抛物线落下，为使水流形状较为漂亮，要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m，如果不需要考虑其他因素，水池的半径为多少？如果水流喷出的抛物线形状与之前的计算结果相同，水池的半径为3.5m，那么为了让水流不会流出水池，水流的最大高度应当为多少？笔者为了让学生更好地理解本问题，特组织同学们对题中各个量进行分析，探索之间的关系，在此基础上画出相应的图形（如下图），确定相应的函数关系。在此过程中让学生求函数中的最大量和最小量，再将计算结果带入实际问题中应用。

通过这样的方式不仅让学生了解题目中的函数关系，而且让学生了解题目中数量关系的变化特征，并将学习的知识逐渐引入生活中应用，体会现实世界中的数学模型建立方式。

3.其他教学内容中数形结合思想的应用

初中数学中其他教学内容同样蕴含数形结合思想，教师在此方面内容教学过程中可以通过数形结合思想的应用突破相应难点，将题目中的重要问题通过图形绘制方式表现出来，让学生从中感受到数形结合的力量，让学生逐渐适应数形结合思想的应用。比如，笔者在《一元一次方程》教学过程中便让学生通过数形结合思想解答相关的问题。

例题：一列火车车身长200米，其在经过隧道的时候时速为60千米每小时，从车头进入隧道到车尾离开隧道共2分钟，求隧道长。

对于此问题的解答莫过于通过图形绘制解答最为方便。笔者带领学生首先绘制了三段线段表示，车头进入隧道之前为一段线段，中间隧道假设为x米，此为一段线段，车位离开隧道之后又是一段线段，此时便可以通过图形列出相应方程式：2*1000=x+200。图形与方程式结合在一起非常形象，学生理解起来非常容易。

结语

数形结合思想作为数学学习的重要思想，应当得到推广和应用，尤其在初中数学教学中，应用价值更高，让学生对问题的理解更深刻，在图形的引导下对抽象问题学得更好。

参考文献：

[1]杨平荣.对数形结合思想在初中函数教学中的作用探讨[J].学周刊，2013，22：144-145.

[2]腾敏.初中数学教学中数形结合思想的运用研究[J].求知导刊，2015，24：132.

[3]周红英.初中数学数形结合思想教学研究[J].考试周刊，2015，10：71.

[4]戴韩.数形结合教学思想在当前初中数学教学中的运用[J].才智，2015，23：210.

[5]蔡冬莲.数形结合思想方法在数学教学中的应用分析[J].低碳世界，2016，22：273-274.