基于广义双曲线分布的人民币汇率波动性研究

吴礼斌，张晓芳

（安徽财经大学数量经济研究所，安徽蚌埠 233030）

基于广义双曲线分布的人民币汇率波动性研究

吴礼斌，张晓芳

（安徽财经大学数量经济研究所，安徽蚌埠 233030）

针对人民币汇率的波动性问题，运用广义双曲线分布，对2006年1月4日到2015年7月24日美元兑人民币汇率的波动特征进行实证分析。研究认为，人民币汇率不仅具有显著的“尖峰厚尾”特点，而且具有波动的非对称性和集群性特征，同时发现GH分布能较为准确地描述和呈现美元兑人民币汇率收益率波动状况的分布情况。

人民币汇率；广义双曲线分布；波动性；波动率过滤模型

汇率波动是汇率动态行为的重要组成部分，该问题国外学者做了诸多研究。Meyer等［1］借助SV模型对英镑汇率的波动特征进行了研究，发现英镑汇率波动性存在着杠杆效应；Bollerselv［2］针对马克和日元的汇率波动特征和相关性等问题，运用GARCH模型进行了研究，在方法应用上，他考虑标准正态分布（Normal）和广义差分分布（GED）等其他更为一般的分布形式下的GARCH模型，而不限于样本分布；Kilic［3］在具有正态逆高斯（NIG）分布的FIGARCH模型下研究了英镑、加元、欧元、日元、马克和法郎等汇率的条件波动特征，将结果与正态分布和t分布等不同分布形式下的GARCH模型和FIGARCH模型进行比较，分析得出具有NIG分布的FIGARCH模型具有更好的拟合优度。

长期以来，中国实行盯住美元的汇率政策，故关于人民币汇率的波动性特征的研究相对较少。2005年7月21日中国汇率制度改革后，学术界对汇率问题的研究增多，学者们不仅研究人民币汇率对宏观经济和微观经济的影响及其动态特征，还关注其波动特性。曹红辉等［4］在随机游走模型下研究了境外人民币无本金交割远期汇率的高频日汇率，并借助ARCH族模型对估计的残差序列进行检验，发现境外人民币无本金交割远期汇率序列具有“尖峰厚尾”和波动集聚等特征；骆珣等［5］运用GARCH模型对美元兑人民币汇率日度数据进行了拟合，研究表明GARCH模型能够较好地呈现汇率制度改革后人民币汇率的条件波动性，而且中国外汇市场存在ARCH效应；夏强等［6］基于双门限非对称GARCH模型对美元兑人民币和非美元货币兑人民币汇率均值和波动过程的非对称特征做了比较，研究表明非美元货币兑人民币汇率的均值和波动过程均呈现出非对称特征；张欣等［7］研究了非人民币汇率的波动特征的对称随机波动模型，结果表明它能够较好地描述美元兑人民币汇率的波动过程中的时变性、持续性和非对称性等特征；宫舒文［8］运用GARCH族模型对美元兑人民币汇率序列进行统计特征分析，并建立模型分析汇率走势状况，发现美元兑人民币汇率具有集群性、非对称性和杠杆效应等特征。

关于汇率波动特征的建模方法有很多，大多数研究是围绕GARCH族模型和SV（随机波动）族模型来展开的。由于广义双曲线（以下简称GH）分布更适合刻画具有尖峰、厚尾、有偏等特点的汇率序列，它不仅能够很好地描述汇率收益率的“真实分布”，而且能显现汇率波动的相关特性，因此本文运用GH分布研究美元兑人民币汇率收益率序列的波动特性。

一、理论模型

（一）常用扰动项分布

金融时间序列，特别是金融资产的收益率序列往往具有时变性、厚尾性等特点，波动聚集现象明显，人民币汇率数据亦是如此。为了刻画人民币汇率收益率序列的这些特征，Engle和Bollerselv等人提出并发展了ARCH和GARCH模型，模型利用过去历史未预期到的残差平方的移动平均来捕获序列的条件异方差性。对波动率模型进行估计时，假设残差分布为正态分布不能有效地解释人民币汇率序列的尖峰厚尾现象，常用的两类厚尾分布分别为广义误差分布（GED）和学生t分布［9］。

1.广义误差分布（GED）

均值为0、方差为1的广义误差分布概率密度函数为：

其中，x表示观测值变量，ω是尺度参数，且ω＝［2（-2*v）Γ（1/v）/Γ（3/v）］0.5，Γ（·）为伽马函数，v是尾部厚度参数。这里，参数v控制着分布的形式，v值不同，对应的分布形式也不同。当v＝2时，GED为正态分布；v＜2时，GED的尾部比正态分布薄；当v＞2时，GED的尾部比正态分布厚，特殊的，当v→∞时为上的均匀分布。

2.学生t分布

学生t分布的密度函数为

其中，n称为t分布的自由度。t分布的尾部比正态分布厚，可以用来描述分布的厚尾特征，但较之正态分布，t分布不具有较为良好的统计性质。

（二）波动率过滤模型

金融时间序列数据通常表现出序列相关性，但对数据的拟合要求其服从独立同分布条件，因此在进行拟合之前，对具有序列相关性的原始数据进行过滤，使过滤后的数据满足独立同分布条件［10］。

本文利用ARMA＋GARCH联合模型对收益率序列进行过滤。ARMA＋GARCH联合模型由条件均值和条件方差两部分构成，自回归移动平均（ARMA）模型反映序列的条件均值，广义自回归条件异方差（GARCH）系列模型刻画序列的条件方差。文中采用ARMA＋GARCH、ARMA＋EGARCH和ARMA＋GJR-GARCH3种模型，在这3个模型中，条件均值模型ARMA（p，q）均可表示为

式中，xt表示时间序列变量，φ0是常数项，i，j分别是xt-i，εt-j的滞后阶数，φi是自回归参数，θi是移动平均项的系数，εt是一个白噪声过程，表示扰动项，p、q分别是自回归项和移动平均项的阶数，均为非负整数。

条件方差模型分别为

第一，GARCH（m，n）：

其中σt表示条件方差，且有，αi≥0（i＝1，…，n）；βj≥0（j＝1，…，m），且分别为ARCH项εt-i和GARCH项σt-j的系数参数，，对系数的约束保证了序列｛xt｝是一个二阶平稳过程；α是常数。

第二，EGARCH（m，n）：

其中，αi＝（i＝1，…，m），βj（j＝1，…，n），g（·）满足Et-1（g（εt））＝0，θ、γ是系数。

第三，GJR-GARCH（m，n）：

其中αi，βi，ci均为参数，αi＞0（i＝1，…，n）；βj＞0（j＝1，…，m）；αi＋ci≥0。

（三）GH分布族

汇率收益率的变化是一个单变量的时间序列，研究和讨论汇率收益率的非线性特性首先要解决的问题是如何捕捉其中所含的非线性的信息。由林清泉等［9］的研究可以得出，GH分布可以有效地补偿线性模型中假设收益率序列服从正态分布所导致的拟合和估计误差。

1.GH分布

定义1：正态均值—方差混合

如果

其中，X是观测值变量，Z～Nk（0，Ik），μ∈Rd是位置参数，混合变量W是非负一维随机变量且独立于Z，γ∈Rd表示漂移参数，结构矩阵∑＝AA′是对称且正定的，矩阵A∈Rd×d，则称X服从多元正态均值—方差混合分布。

定义2：GH分布

在定义1中，若混合变量W服从广义逆高斯（GIG）分布，则服从广义双曲线分布［9］。这里，GIG分布的概率密度函数为

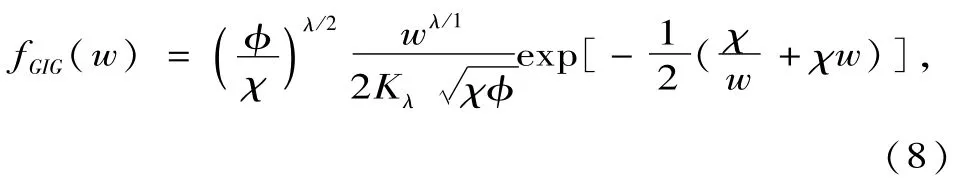
由定义1知：

也就是说在给定W的条件下，X的条件分布服从均值为μ＋wγ、方差为w∑的正态分布。

d维GH分布的联合概率密度函数为

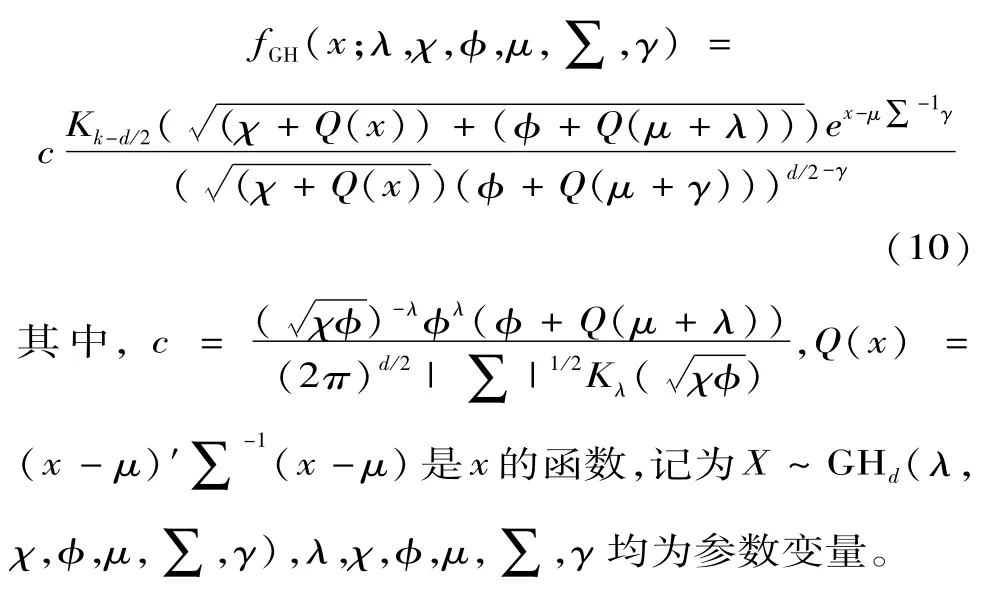
2.GH分布的参数表示方法

GH分布的参数表示方法有很多种，本文旨在拟合单变量的汇率收益率序列，因此主要介绍一种一元GH分布的参数表示方法GH（λ，，μ，∑，γ）。在（6）式中，令E（W）＝1，＝，则

于是可以得到GH分布的一种参数表示形式，记作：X～GH（λ，，μ，∑，γ）。本文实证部分运用该参数表示方法。

3.GH分布参数的极大似然估计

令∑＝1，d＝1，根据式（10）中的概率密度函数，构造对数似然函数，表示为：

当对数似然函数的维数超过3时，便难以通过直接最大化来估计参数，根据Alexander等［10］研究，可以运用EM算法来估计（12）中的参数值。EM算法是解决“不完全数据”（实际可获得数据）极大似然估计问题的通用迭代算法，每一次迭代分为两个步骤：计算条件期望；极大化目标函数。

二、实证分析

（一）数据说明与统计描述

2005年7月21日中国实行汇率制度改革，考虑到汇改前后汇率收益率分布的不同，选取了2006年1月4日到2015年7月24日的美元兑人民币的汇率中间价数据作为样本（数据来源于国家外汇管理局网站），共2 336个数据。对数据预处理，将美元兑人民币汇率收益率定义为：

式中，rt表示的汇率中间价，xt为汇率日收益率。

首先对汇率收益率数据xt做ADF单位根检验，发现其是平稳的，变量xt的统计性描述结果见表1。

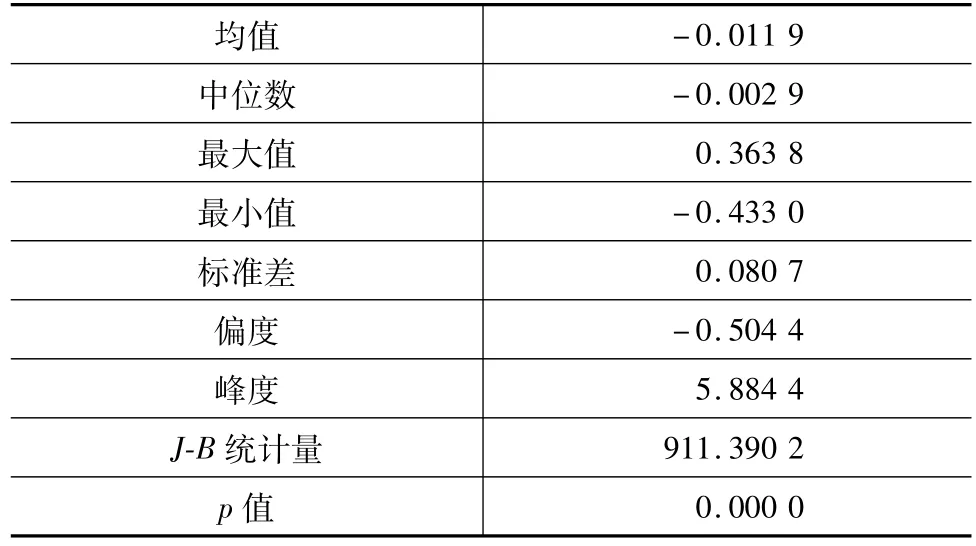
表1 美元兑人民币汇率收益率的基本统计特征描述

由表1可知，汇率收益率数据的偏度和峰度分别为-0.504 4和5.884 4，说明其表现出厚尾、尖峰的特征。偏度为负说明样本分布左偏，左偏的原因主要是人民币一直面临升值的压力，表现为汇改以后人民币汇率一直在下降。J-B统计量值为911.390 2，检验的p值很小，拒绝服从正态分布的原假设。

作美元兑人民币的汇率中间价和美元兑人民币汇率收益率的序列图，分别如图1、图2所示。结合原始数据，可以看出，美元对人民币的汇率中间价从2005年7月汇率改革之后，总体呈现出明显的升值趋势，即汇率中间价在下降，但2008～2010年汇率升值过程暂停，这是因为受全球金融危机和经济增长缓慢等影响；由曲线的陡峭程度可知，汇率的升值速度开始较快，在2010年之后比2008年之前慢。由图2可得，美元兑人民币汇率收益率序列具有和波动聚集性，在2008～2010年汇率升值暂停期间，汇率收益率的波动幅度也较小。

图1 美元兑人民币的汇率中间价序列图

图2 美元兑人民币汇率收益率序列图

（二）波动率模型过滤

由统计性描述知，美元兑人民币汇率收益率序列具有非正态性，本文首先采用ARMA＋GARCH在正态分布、t分布以及GED分布3种分布形式下的联合模型对序列进行过滤，然后检验拟合模型的残差项是否满足独立同分布的假设，也就是对过滤后的标准误差项进行ARCH。表2为ARMA＋GARCH模型联合估计在3种分布形式（Normal，t，GED）下得出的ARCH显著性检验的统计指标（分别取滞后阶数为3，5，7），可知各滞后阶数的p值均大于临界值0.05，说明这9个模型完全通过了ARCH效应检验，这说明模型产生的标准误差项是独立同分布的。

表2 美元兑人民币中间价模型标准误差项ARCH效应检验的p值

选取上述通过ARCH效应检验的模型，进一步的分析残差数据的平稳性，图3给出了美元兑人民币汇率收益率ARMA（1，1）＋GARCH（1，1）＋Normal模型估计后的标准误差平方项的自相函数图，可见模型估计后的残差项趋于平稳，说明模型对残差的提取比较充分，标准误差项序列不再具有长记忆性。

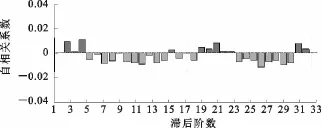
图3 ARMA（1，1）＋EGARCH（1，1）＋Normal模型标准误差平方项自相关函数图

表3为美元兑人民币汇率收益率数据经过不同分布形式的模型拟合的标准误差项的均值、方差、偏度、峰度的经验统计量，可以看出，汇率收益率经过模型估计后的标准误差项样本表现出负偏度，峰度值略高于3，且模型之间的标准误差项偏度和峰度值的波动不大。

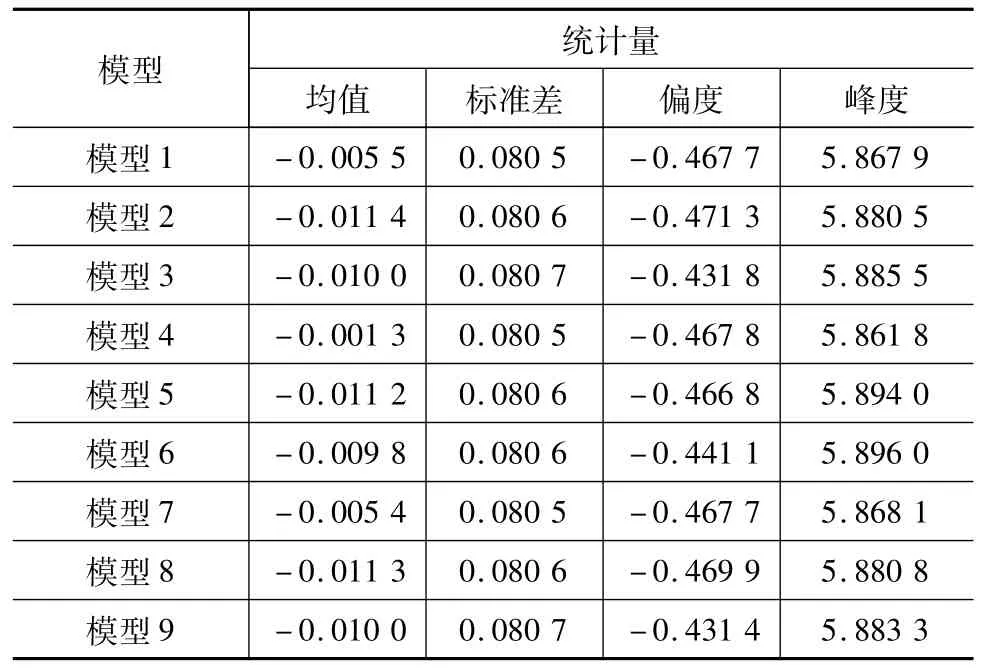
表3 汇率收益率模型估计后的残差序列描述性统计

（三）标准误差项分布的拟合

为了对汇率收益率数据进行更精确地描述，通过引入分布及其子类分布对标准残差项进行拟合，利用上面9个模型中偏度和峰度较小的模型2（ARMA（1，1）＋GARCH（1，1）＋t）和模型4（ARMA（1，1）＋EGARCH（1，1）＋Normal）对美元兑人民币汇率收益率数据进行拟合，具体的参数估计见表4。

为方便直观地观察各分布假设下对样本数据的拟合情况，本文画出了汇率收益率数据经过不同模型估计出的标准残差序列的GH分布概率密度曲线、根据样本正态分布密度曲线和基于非参数核估计的样本经验分布密度曲线。图4和图5是汇率收益率经过模型2和模型4估计得出的残差序列基于GH分布拟合后的3种概率密度曲线，从图4和5可以看出，GH分布拟合曲线和样本经验分布密度曲线基本重合，表明GH分布对残差序列拟合效果明显比正态分布好，表明GH分布对金融时间序列的尖峰厚尾等现象具有较强的描述能力。

表4 汇率收益率数据的GH分布估计参数结果

图4 基于模型2估计的残差序列分布密度曲线

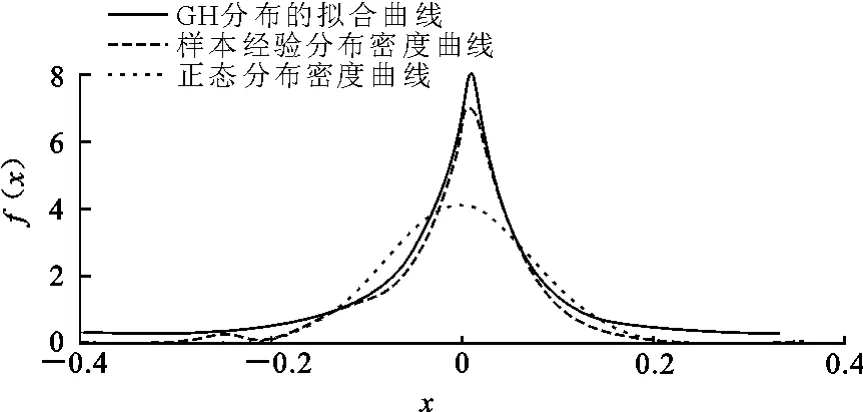
图5 基于模型4估计的残差序列分布密度曲线

图6 基于模型2的残差序列的GH分布分位数图

图7 基于模型4的残差序列的GH分布分位数图

图6和图7分别是汇率收益率序列通过模型2和模型4估计后的残差序列的分布分位数图，从中可以明显地看出分布拟合的数据基本集中在45°线附近，其拟合效果明显优于正态分布。

三、结语

线性时间序列在建模中具有规范性和方便性，故在金融资产收益率的研究当中，往往假设它服从正态高斯分布，但是现实金融数据序列通常表现出尖峰、厚尾、有偏等特征。在线性架构下进行建模会导致对“真实收益率”分布的错误认识，本文在已有文献的基础上，介绍了几种常见的分布形式和波动率过滤模型，然后选以美元兑人民币汇率收益率为对象，在对汇率收益率序列进行波动率模型估计后，提取残差扰动项，利用广义双曲线分布进一步拟合扰动项的分布特征，分析发现人民币汇率波动的非对称性和集群性特征。虽然人民币还没有完全市场化，但通过统计性描述得出了美元兑人民币收益率序列具有显著的“尖峰厚尾”的特点，尤其是左厚尾的特点；从汇率收益率序列图可以看出其呈现高收益集群出现的特征，表明其呈现波动集群性。通过密度函数曲线的比较可知，在研究美元兑人民币汇率波动特征时，GH分布比正态分布更为有效。然而本文是对提取的波动率模型的残差扰动项进行GH分布拟合的，而对人民币汇率收益率的时变波动性质等缺乏具体的讨论，此外，在以后的研究中我们将关注GH分布在汇率风险方面的应用，诸如基于GH分布的VAR方法对人民币汇率风险的度量等研究。

［1］Meyer R，Yu J.BUGS for a Bayesian analysis of stochastic volatility models［J］.Econometrics Journal 2000，3（2）：198-215.

［2］Bollerslev T.Generalized autoregressive conditional Heteroske dasticity［J］.Journal of Econometrics，2003（31）：307-327.

［3］Kilic R.Conditional volatility and distribution of exchange rates GARCH and FGA-RCH modelswith NIG distribution［J］.Studies in Nonlinear Dynamics＆Econometrics，2007，11（3）：1-31.

［4］曹红辉，王深.人民币汇率预期：基于ARCH族模型的实证分析［J］.国际金融研究，2008（4）：52-59.

［5］骆珣，吴建红.基于GARCH模型的人民币汇率波动规律研究［J］.数理统计与管理，2009（2）：295-300.

［6］夏强，刘金山.基于MCMC算法的人民币汇率市场的分析——双门限非对称GARCH模型的应用［J］.数理统计与管理，2012（3）：419-42.

［7］张欣，崔日明.基于非对称随机波动模型的人民币汇率波动特征研究［J］.国际金融研究，2013（1）：28-37.

［8］宫舒文.基于GARCH族模型的人民币汇率波动性分析［J］.统计与决策，2015（12）：159-161.

［9］林清泉，张建龙.金融时间序列建模和风险度量——基于广义双曲线分布的方法［M］.北京：中国人民大学出版社，2010.

［10］Alexander J M，Frey R，Embrechts P.Quantitative risk management［M］.Princeton：Princeton University Press，2005.

Research on RMB exchange rate volatility based on GH distribution

WU Li-bin，ZHANG Xiao-fang
（Institute of Quantitative Economics，Anhui university of Finance and Economics，Bengbu 233030，Anhui，China）

Regarding the volatility of RMB exchange rate，this paper investigated the characteristics of US$/RMB exchange rate volatility from January 4，2006 to July 24，2015，using generalized hyperbolic（GH）distribution.It is found that RMB exchange rate not only has the significant“leptokurtosis and fat tail”characteristics，but also has fluctuating asymmetry and clustering characteristics.At the same time，it is found that GH distribution can describe and present the distribution of US$/RMB exchange rate volatility precisely.

RMB exchange rate；generalized hyperbolic（GH）distribution；volatility；volatility filteringmodel

F832.6

：A

：1671-6248（2016）04-0062-06

2016-04-14

安徽省高等学校自然科研项目（KJ2013Z001）；安徽财经大学重点研究课题（ACKY1402ZD）；安徽财经大学研究生科研创新基金项目（ACYC2015082）

吴礼斌（1962-），男，安徽枞阳人，副教授。