基于LSSVM的电子装备故障预测研究

张 波,陈岩申,李艳青

(海军青岛雷达声纳修理厂，山东 青岛 266100)

基于LSSVM的电子装备故障预测研究

张 波,陈岩申,李艳青

(海军青岛雷达声纳修理厂，山东 青岛 266100)

针对电子装备的故障信息不足，故障发生率高等特点，通过故障预测有效的监测设备故障状态以及发展趋势，实现对设备的事先维修，避免重大事故的发生，提高电子设备的安全性;对电子装备故障预测进行了分析，提出了一种基于最小二乘支持向量机(LSSVM)的故障预测方法;首先介绍了LSSVM故障预测算法的基本原理和预测流程；然后，对整个电子装备的故障预测研究可以从一个类似的模拟带通滤波器电路故障预测研究出发，将该元件容差设为不同范围来定义电路的不同故障状态，将LSSVM方法与最小二乘法、支持向量机法对电路的不同状态进行预测，可以得到不同状态的预测值，研究结果表明提出的方法能够实现模拟电路的缓变故障预测，且预测效果较好。

最小二乘支持向量机;故障预测;电子装备;故障预测与健康管理

0 引言

故障预测与健康管理(prognostic and health management，PHM)是一种全面故障检测、隔离和预测及健康管理技术，它的引入不仅仅是为了消除故障，而是了解和预测故障何时、何处可能发生以及故障类型，使得系统在尚未发生故障之前，就能依据系统的当前健康状况决定何时维修， 从而实现自助式维护系统，降低使用和维护费用的目标。故障预测是PHM的重要组成部分，故障预测相关技术的研究和发展为PHM理念提供有效的理论根据，从而实现从传统的基于传感器的故障诊断转向基于智能系统的故障预测。

现代的电子装备结构越来越复杂化，可能发生的故障越来越多样化，其故障相对于机械设备来说更难检测出来，因此需要探索出一种有效可行的基于PHM的电子装备故障预测方法，通过故障预测有效的监测设备故障状态以及故障发展趋势，实现对设备的事先维修，避免重大事故的发生，提高电子设备的安全性。本文主要是开展基于最小二乘支持向量机(least squares support vector machine，LSSVM)对其电子装备进行故障预测研究，实现对缓变故障的预测。

1 LSSVM故障预测模型和预测步骤

1.1 LSSVM故障预测模型

面对大量数据时，支持向量机(Support Vector Machine，SVM)很难对优化问题进行求解，因此Suykens等人提出了LSSVM来完善SVM的不足，LSSVM把约束条件由不等式变成等式，把非线性回归问题转换成线性回归问题，将误差平方和应用到目标函数中，再通过KKT(Karush-Kuhn-Tucker)最优条件把SVM的优化问题转换为对线性方程组的求解问题，提高了训练速度和收敛精度。

建立LSSVM故障预测模型，首先把训练数据输入模型中，通过相空间重构确定输入输出的对应关系，建立了预测模型，再把测试数据输入模型进行预测，从而实现对未来某一时刻的预测，下面是LSSVM的学习样本：

(1)

从式(1)中发现输入与输出是一一映射的，其中f:Rm→Rm，m为嵌入维数，m的确定根据最终预测误差(FPE)准则。

(2)

其中：

可以看出FPE(k)是随着k变化而变化的，当FPE(k)取得最小值时，则最优解m就是最佳嵌入维数m=kopt。

开始LSSVM模型训练，得到LSSVM回归函数为：

(3)

得到第1步预测为:

(4)

则第2步预测为:

(5)

以此类推，则第k步的LSSVM预测模型为:

(6)

1.2 LSSVM故障预测流程

基于LSSVM故障预测步骤如下：

1)确定特征参数和数据处理。对于给定的预测系统进行分析，找出能够反映系统状态变化的特征参数，获得样本数据；对样本数据预处理，得到模型训练和测试所需要的数据；为了避免样本数据数量级的影响，可以先对所有样本数据归一化处理。

2)确定模型参数。首先根据需要选择合适的LSSVM预测模型，然后输入LSSVM的学习样本，根据式(2)确定嵌入维数，通过学习得到模型输入输出映射关系。其中模型参数的选择尤为重要，本文中采用的核函数是径向基核函数，同时调整参数γ和核参数σ2对LSSVM的性能好坏也起到决定性的作用。当调整参数γ越大时，训练样本在模型中的拟合程度越好，当调整参数γ越小时，相应的模型复杂度越低。而核参数σ2的取值是影响拟合曲线光滑程度的关键。

3)模型训练。把样本数据划分成训练数据和测试数据，将训练数据输入模型进行训练。

4)预测。把测试样本输入模型进行预测，输出值即预测值。

5)评价预测模型。对得到的预测结果进行评价分析，如果不能达到理想的预测结果，则重新进行训练，直到得到较为理想的预测结果。

本文采用的评价指标为绝对误差和相对误差。绝对误差(Absolute Error，AE)：

,...n

(7)

相对误差(Relative Error，简称RE)：

,...,n

(8)

LSSVM故障预测流程如图1所示。

图1 基于LSSVM故障预测流程

2 LSSVM在电子装备故障预测中的应用案例

由于电子装备的退化状态数据很难获得，对整个电子装备的故障预测研究可以从一个类似的模拟电路故障预测研究出发， 如图2所示为Sallen-Key带通滤波器，采用PSPICE软件对电路仿真，所有R的容差为±10%，C的容差为±5%。

图2 Sallen-Key带通滤波器

2.1 特征参数的选取

对图2的模拟电路来说在正常工作状态下每个元件都有规定的容差范围，当元件超出规定的容差就可能出现故障。在一个电子装备的实际电路中可能会由大量的元件组成，每个元件的变化都可能会导致故障的发生，但每个元件改变多少对电路输出影响才会明显，这就由元件灵敏度的大小来决定了。灵敏度越大，当改变元件大小或容差对输出影响越大。本文采用PSPICE中的灵敏度分析对图2的模拟电路中各元件进行分析，选择灵敏度高的元件作为模拟故障渐进过程的元件。

首先对电路进行交流仿真，本文采用的信号源为幅值为2 V，相角0o的正弦波信号。各元件均工作在正常容差范围内，测试点为电路输出点V0，选取频响输出电压作为监测信号，图3为该模拟电路的交流仿真结果。

图3 交流仿真结果

通过对该电路进行灵敏度分析可知，对电路输出带宽和最大增益影响最大的是C1、C2，再通过参数扫描来确定要改变的元件。

分别对C1、C2取不同数值，观察C1、C2取不同值时对电路输出波形的影响，输出波形如图4、图5所示。

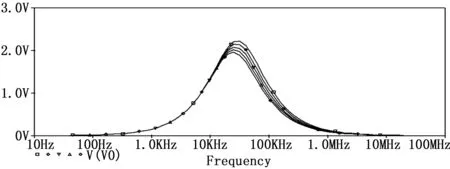
图4 C2取不同值电路的输出波形

图5 C1取不同值电路的输出波形

如图4、图5所示，当C1、C2取标称值和不同值时，电路的输出波形变化都很明显，C1的波形变化主要集中在100 Hz～100 KHz之间，C2的波形变化主要集中在10 KHz～10 MHz之间，本文选取C2作为测试元件，将C2的不同变化作为特征参数。

2.2 状态设置与特征提取

本文只考虑C2的变化对整个电路系统的影响，其他元件参数均在正常容差内变化，测试点为端节点V0，对该电路进行频率响应分析。

1)当C2的容差变化范围为[-5,+5]%，C2在正常的容差变化范围内，为正常状态；

2)当C2的容差变化范围为[5,10]%，C2出现微弱故障，为退化状态1；

3)当C2的容差变化范围为[10,15]%，C2逐渐偏离正常状态，为退化状态2；

以此类推

4)当C2的容差变化范围为[45,50]%，C2将无法正常工作，为完全故障状态；

即C2的容差变化范围分别为[5,10]%，[10,15]%，[15,20]%，[20,25]%，[25,30]% [30,35]%，[35,40]%，[40,45]%，[45,50]%来模拟该电路系统的状态退化过程，加上正常状态共设置了10种状态，分别对得到的每种状态进行50次蒙特卡罗(MC)分析，设置频率变化范围为100 Hz～10 MHz，图6为各状态的仿真结果。

结合图4和图6发现在10～400 kHz之间C2的变化对电路输出的影响最为明显，因此分别对每个状态取10 kHz、25 kHz、50 kHz、80 kHz、100 kHz、150 kHz、200 kHz、250 kHz、300 kHz、400 kHz对应的10个频响电压幅值构成一个10维的电压特征向量，作为原始特征向量。其中每种状态有50组特征向量，30组作为训练样本，20组作为测试样本。

2.3 模型训练与故障预测

对正常状态和各退化状态取得的10维电压特征向量取平均值，构成训练数据，表1为各状态在对应频率下输出电压的平均值，1～10分别代表电路的正常状态、退化状态2～9和完全故障状态。

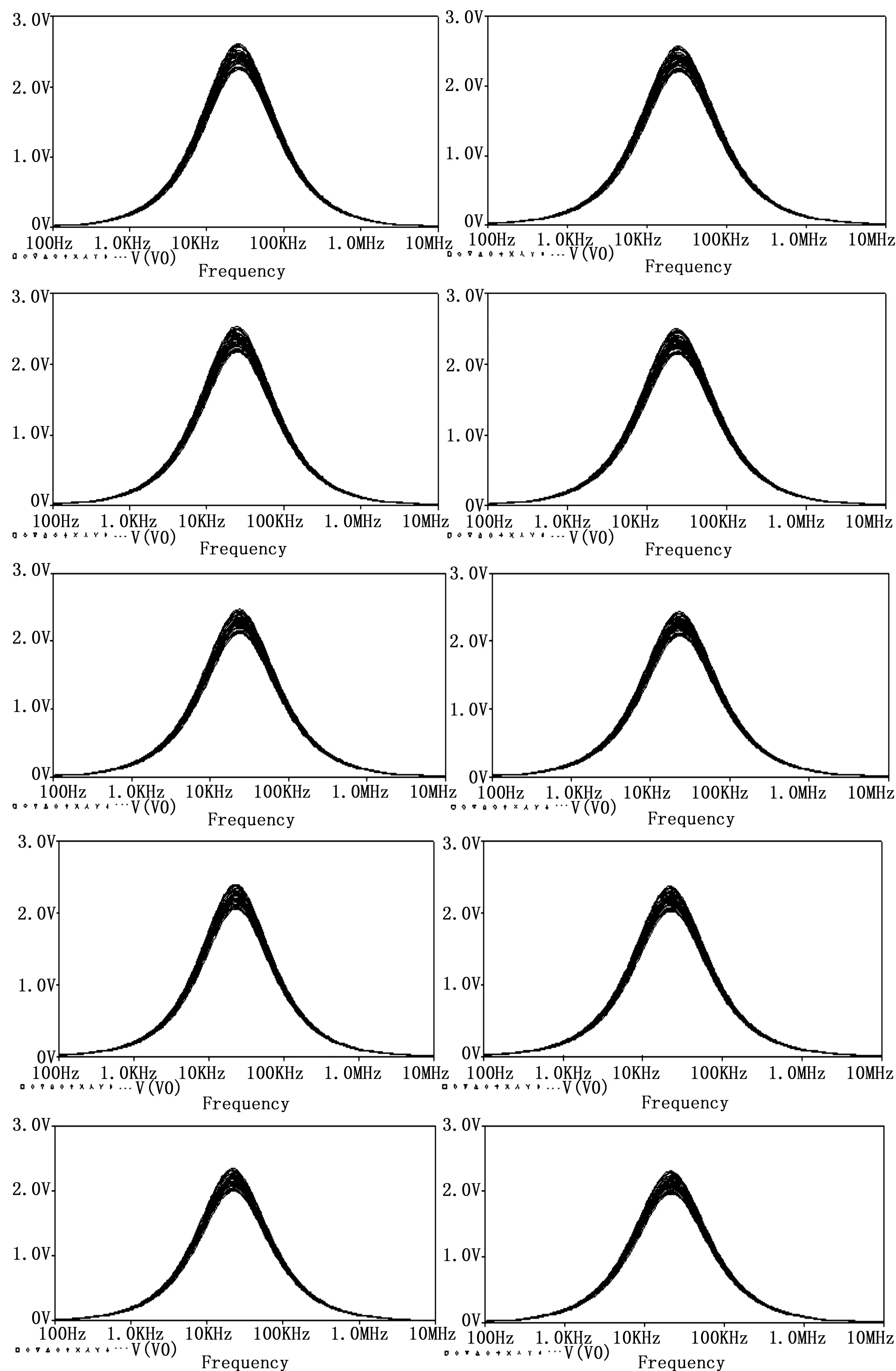
图6 各状态的仿真结果

从表1可以看出随着该电路的状态逐渐退化，其所对应的各频率下的输出电压也逐渐降低，因此证明了通过改变C2的容差来模拟状态退化过程是合理的。

通过对训练样本训练，确定嵌入维数为4，采用径向基核函数，通过模型训练和对测试样本的预测确定(σ2，γ)为(0.25，100)。从表1中选取25 kHz(各状态样本中最大值)、50 kHz(同一状态下相邻频率之间变化最大的)的各状态数据对其进行LSSVM故障预测。选取状态1～4的数据作为第一次训练样本，得到状态5的预测值，再选取状态2～5的数据作为第二次训练样本，得到状态6的预测值，以此类推，得到状态5～10的预测值。作为对比，分别利用最小二乘法(Least Squares，LS)算法、SVM算法和LSSVM算法对状态5～10进行回归预测，实际曲线和各预测算法所得到的曲线如图7、图8所示。

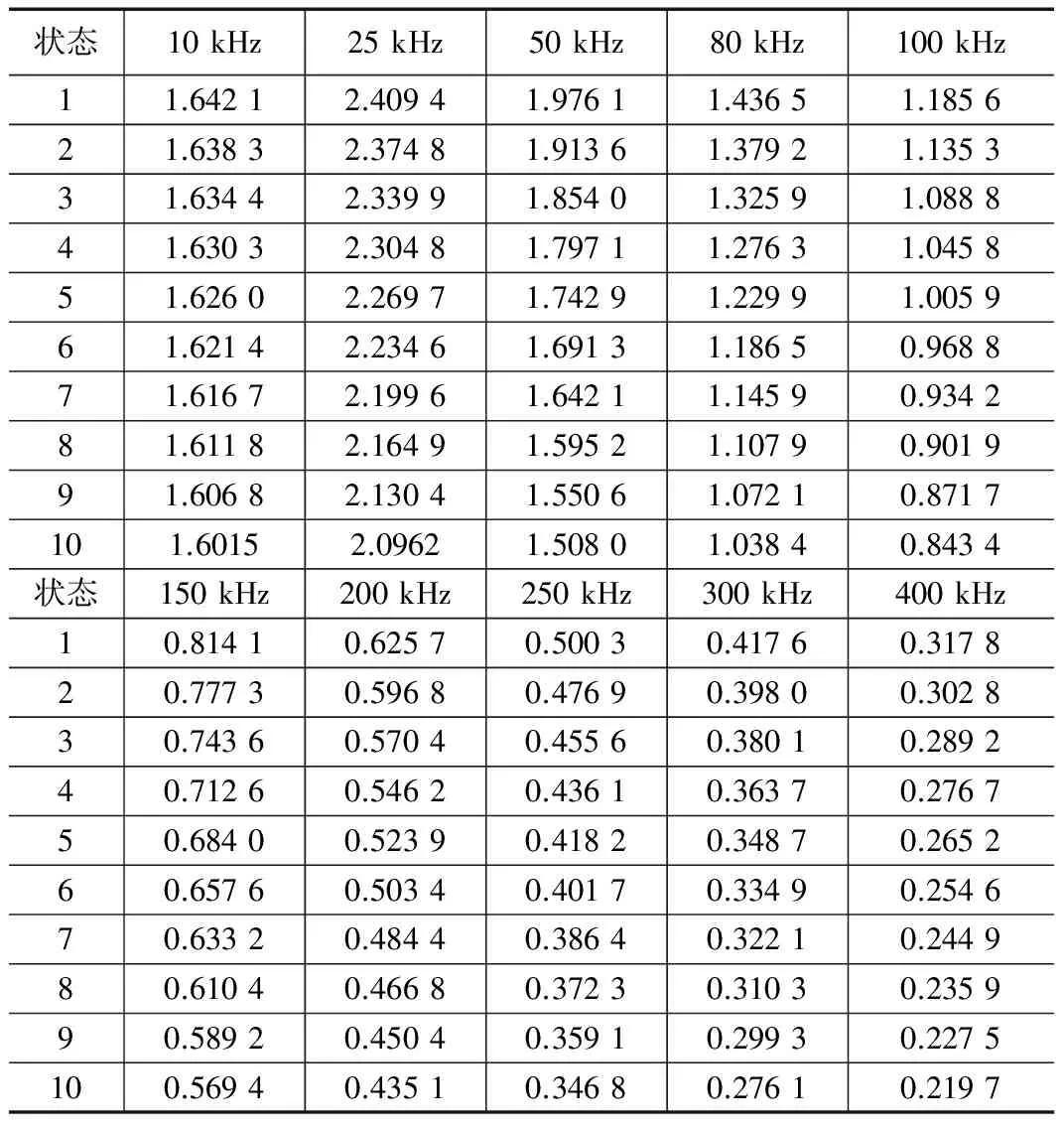
表1 模拟电路在各状态下输出电压平均值

图7 25 kHz下各状态实际与预测曲线的比较

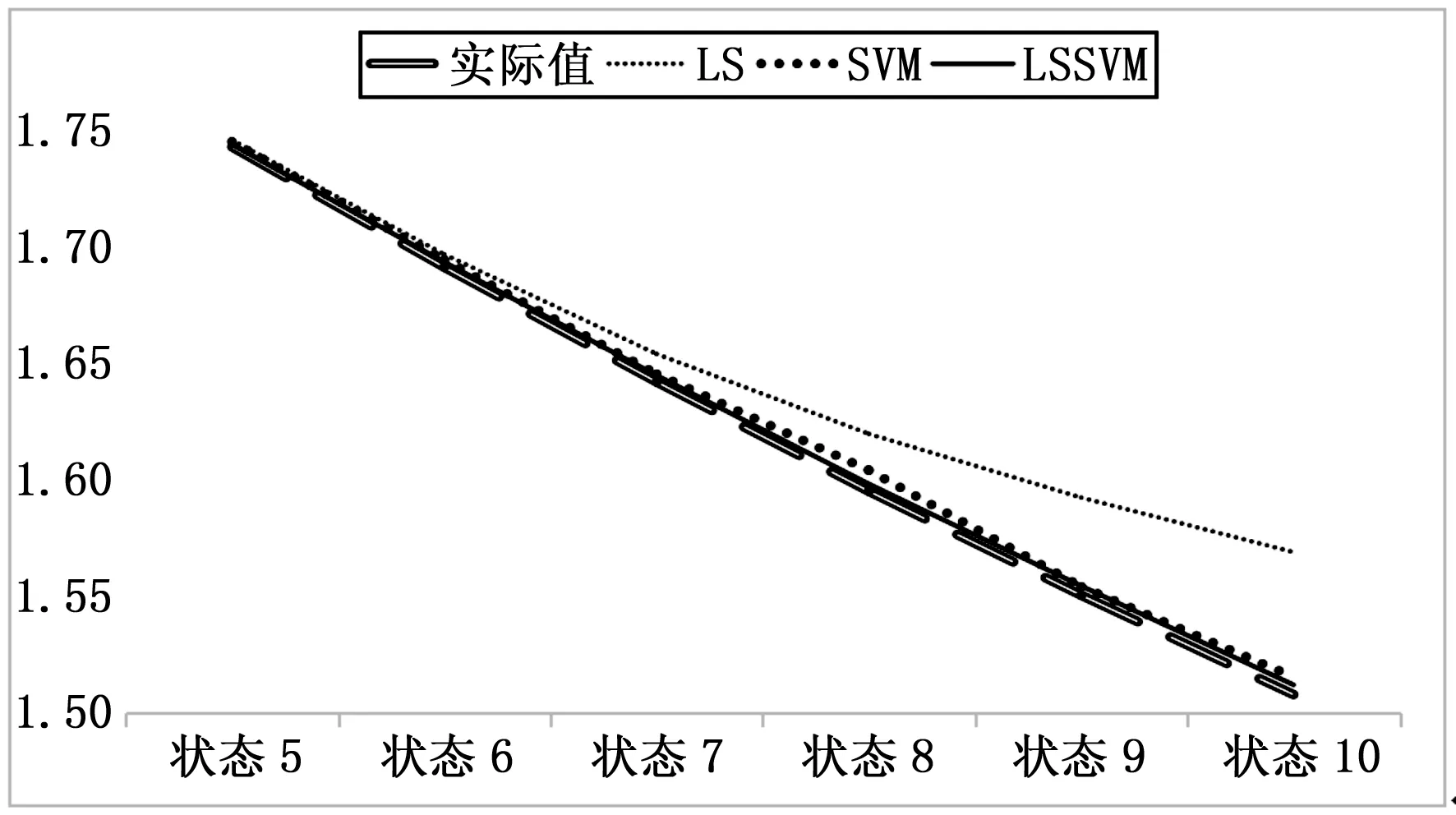
图8 50 kHz下各状态实际与预测曲线的比较

表2、表3为各状态在25 kHz、50 kHz下分别利用LS算法、SVM算法和LSSVM算法的预测结果和相对误差。

2.4 预测结果分析

根据图7与图8中各算法得到的预测结果与实际曲线对比可知，前3个状态中3种算法的预测值与实际值都很接近，随着预测步数的增加，LS算法的预测逐渐偏离实际值，预测精度随之降低；SVM、LSSVM算法预测结果较理想，拟合效果好。通过表2与表3可知，LS算法在前3个状态预测误差均小于1%，能够很好的实现预测，但对后3种状态的预测则偏离实际值很远，甚至预测值远大于状态实际值，如表2中应用LS算法对状态9的预测值与状态7的实际值几乎一样，这样就不能准确的实现故障预测，因此LS算法较适合短期预测。SVM算法的预测误差均小于0.6%，LSSVM算法的预测误差在0.3%左右，两者都能较好的实现故障预测，但LSSVM算法的预测效果更佳，更适合模拟电路故障状态预测。

表2 各状态在25 kHz下的预测结果和相对误差

表3 各状态在50 kHz下的预测结果和相对误差

3 结论

本文针对电子装备的故障预测方法进行了研究，首先介绍了LSSVM故障预测算法的基本原理和预测流程；然后，对整个电子装备的故障预测研究可以从一个类似的模拟电路故障预测研究出发，因此本章采用对带通滤波器进行研究，通过灵敏度分析和参数扫描确定要改变的电路元件，再将该元件容差设为不同范围来定义电路的不同故障状态，分别采用LS、SVM、LSSVM对电路的不同状态进行预测，可以得到不同状态的预测值；最后针对LSSVM预测性能进行分析，结果表明本章提出的方法能够实现模拟电路的缓变故障预测，且预测效果较好。

[1] Yin M， Ye X H， Chen S C. Sensor Selection and Location Scheme for Prognostic and Health Management[J]． Sensors and Transducers，2013，158(11)：230-235．

[2] 王红霞，潘红兵，叶晓慧.多故障的测试序列问题研究[J]．兵工学报，2011，32(11)：1518-1523.

[3] 谢松汕．基于HMM/SVM的风电设备故障趋势预测方法研究[J]．计算机测量与控制，2014，22(1)：39-41．

[4] 王 承．基于神经网络的模拟电路故障诊断方法研究[D]．成都：电子科技大学，2005.

[5] 高亚龙，张 磊，柴 波．基于PHM的电子系统测试性设计与故障诊断技术[J]．电子技术与软件工程，2014，43(7)：110-111．

Research of Fault Prognostic Based on Least Squares Support Vector Machine for Electronic Equipment

Zhang Bo,Chen Yanshen,Li Yanqing

(Naval Qingdao Repair Workshop of Radar Sonar, Qingdao 266100,China)

Because fault information of the electronic equipment is insufficient, high incidence of failure, through fault prediction and effective monitoring equipment failure status and development trend, the realization of the equipment maintenance, to avoid the occurrence of major accidents, improve the safety of electronic equipment. Fault prediction of electronic equipment is analyzed, and a fault prediction method based on least square support vector machine (LSSVM) is proposed.Firstly it introduces the basic principle and the fault prognostic algorithm of the LSSVM process. Then, fault prognostic research for the electronic equipment can be from a similar analog band-pass filter circuit. Compared to the least square method and support vector machine method, LSSVM method is applied to the different fault condition of the circuit, which obtained the different results.It shows that the proposed method can achieve graded fault prognostic for the analog circuit, and has the better prediction effecting.

least squares support vector machine; fault prognosis;electronic equipment; prognostic and health management

2016-07-11；

2016-07-25。

张 波(1974-)，男，山东安丘人，研究生，高级工程师，主要从事电子装备自动测试与故障诊断方向的研究。

1671-4598(2016)12-0106-04

10.16526/j.cnki.11-4762/tp.2016.12.030

TP274

A