无人水下航行器推进器故障定位研究

廖文献，黄兴利，刘富樯

(1.浙江工贸职业技术学院 信息传媒学院，浙江 温州 325003； 2.西北工业大学 自动化学院，西安 7100722；3.重庆大学 机械工程学院，重庆 400044)

无人水下航行器推进器故障定位研究

廖文献1，黄兴利2，刘富樯3

(1.浙江工贸职业技术学院 信息传媒学院，浙江 温州 325003； 2.西北工业大学 自动化学院，西安 7100722；3.重庆大学 机械工程学院，重庆 400044)

为保障无人水下航行器(UUV)在复杂海洋环境中航行的安全，降低因推进器故障而可能带来的风险，研究UUV配置多推进器执行使命时，推进器的故障定位问题，已为容错控制提供详细的故障信息，从而提高UUV在面临推进器故障时的容错能力;从UUV的非线性动力学模型出发，利用线性估计方法获得模型控制输入中的加性故障因子；采用基于几何相关性分析的方法，设计了UUV同一平面内多推进器的故障定位算法，并提出了故障定位约束条件；结合加性故障描述因子与故障定位约束条件，通过故障定位算法获得各推进器的故障情况；通过搭建Simulink仿真实验，对UUV同一平面内多推进器共同执行使命时的故障进行定位分析，准确定位了已发生故障的推进器，验证了所提算法的可行性与有效性。

无人水下航行器；推进器；故障定位；冗余

0 引言

无人水下航行器(UUV)是人类进军海洋的智能系统之一，其高度自主的能力有利于拓展人类在水下的活动作业能力。然而海洋环境复杂多变，运动中的UUV极易发生故障，犹以推进器故障为甚。推进器发生故障后可能造成UUV的丢失或者损坏，及时有效的故障定位有利于采取有效的容错控制措施，保障UUV水下作业的安全。

目前，以UUV推进器作为故障定位研究对象的研究较为丰富，如Mangoubi等[1]采用Gauss-Markov模型定义UUV推进器的故障，以滤波器获得推进器的故障残差，将残差与阈值进行对比实现故障定位；Alessandri等[2]以扩展卡尔曼滤波器估计UUV左右两侧推进器的故障残差，进行推进器故障的比较定位；Corradini等[3-5]采用用滑模量来表征推进器的故障残差，并采用几何分类法建立以滑模量为输入的分类函数，对比分类实现推进器的故障定位；Omerdic等[6]建立推进器期望转速、实际转速和电机电流的三维离线数据库，在实际运行时采用模糊分类的方式进行推进器的故障定位；Cristofaro等[7]建立了UUV的状态估计误差模型，通过估计误差构建故障残差，将残差与阈值对比可直接实现推进器的故障定位。

然而，现有文献并未对UUV的多台推进器进行几何相关性角度的故障定位分析，缺少相关方面的研究结果。据此，本文基于几何相关性分析，开展UUV多台推进器的故障定位研究，补充在多台推进器定位研究方面的不足。

1 问题阐述

本文研究形如图1所示的UUV[8]，推进器配置在UUV的水平面和平行于竖轴的方向上，如图2所示。

图1 配置多台推进器的UUV 图2 推进器配置情况

UUV的动力学模型可表述[9]为:

(1)

式中,各参量的定义见文献[10]。当推进器发生故障时，式(1)中τ将受故障影响而发生变化，可对τ中的故障信息进行如下描述与估计：

引理1[10]：如果τ中所携带的故障以式:

τ=τ*+f

(2)

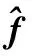
(3)

其中:

(4)

K为正定对角阵。

对于推进器配置形如图2的UUV，τ为:

(5)

其中，

ci=cosαi,si=sinαi,xj=rjsinθjsinδj

yj=rjsinθjcosδj,zi=lisin(αi-βi)

tX=[T1…Ti…Tk]T,tZ=[Tk+1…Tj…Tm]T

当推进器i发生故障时，推力Ti(i∈[1,m])不等于其期望值，可基于式(5)对Ti进行分析，实现UUV故障推进器的定位。

2 主要结论

2.1 xBoByB平面推进器配置分析

从式(5)中提取xBoByB平面的故障方程组:

(6)

当xBoByB平面推进器发生故障时，可通过对比tX与期望动力向量，实现故障推进器的定位。

若xBoByB平面仅1台推进器(k=1)，那么解式(6)可得出tX。对于k≥2的情形：

1) 当k=2时，式(6)中:

(7)

若rankBX=1，2台推进器构成冗余关系；若rankBX=2，由式(6)可得2台推进器推力:

(8)

或:

(9)

2) 当k=3时，式(6)中:

(10)

若rankBX<3，存在推进器冗余；若rankBX=3，可得推进器推力:

(11)

3)当k>3时，式(6)中未知变量的个数多于方程个数，故tX的解不唯一，无法采用上述矩阵求逆的方式对故障推进器进行定位。

当冗余的推进器不同时发生故障时，可采用下文对xBoByB平面故障推进器进行定位分析。

2.2 xBoByB平面故障推进器的定位

本节针对不同台数推进器同时故障的情形进行分析。

2.2.1 单台推进器故障的情形

当xBoByB平面无推进器故障时，

(12)

若推进器i发生故障，式(6)减去式(12)得:

(13)

(14)

当且仅当:

(15)

若能表明式(15)与仅i故障相对应，那么由式(15)可判断i是否故障。据此，有如下定位定理：

定理1：如果xBoByB平面推进器i使得式(15)成立，那么i发生故障，故障的加性描述可由式(14)求得。

证明：

已知式(15)是推进器i故障的必要条件，现仅需证明其充分性即可。考虑式(15)成立时，实际为推进器j，或者组合(i,j)，甚或组合(p,q)发生故障。

1)j或(i,j)故障，那么:

(16)

其中:pij为j故障所占比例。当pij=1时，故障仅发生在j上；当pij∈(0,1)时， i与j均发生了故障。据式(16)可得:

(17)

可解出:

(18)

当l=-1或l=1时，有zi=-zj，i与j在同一直线上，推力方向相反，通常不会同时工作，故不会同时故障；当l=0时，两推进器重合，于实际情况不符。可知，i工作时，j或(i,j)故障均不成立。

2) 推进器p和q故障，那么:

(19)

其中:fp与fq分别为p与q故障的加性描述，可得:

(20)

或:

(21)

以及约束:

(cpsq-cqsp)zi-(zpsq-zqsp)

ci-(zqcp-zpcq)si=0

(22)

式(22)成立时，i与组合(p,q)构成冗余关系。当i与(p,q)不同时运行，或者p与q同时故障的概率较i低时(通常2台推进器同时故障的概率较1台的低1个数量级)，可知式(15)成立时，i故障。

证毕。

2.2.2 两台推进器同时故障的情形

若推进器p和q故障，式(6)减去式(12)得:

(22)

其中:fp与fq同式(19)。可得故障的加性描述:

(23)

或:

(24)

以及约束:

(cpsq-cqsp)fN-(zpsq-zqsp)fX-

(zqcp-zpcq)fY=0

(25)

若能表明式(22)与(p,q)故障相对应，那么由式(25)可判断p和q是否同时故障。据此，有如下定理：

定理2：如果xBoByB平面推进器p和q使得式(25)成立，并且(p,q)的冗余推进器不同时运行，或者故障率比(p,q)的低，那么p和q发生故障，故障的加性描述可由式(23)或(24)求得。

定理2的证明过程与定理1类似，本文略。

2.2.3 三台及以上数量推进器故障的情形

考虑xBoByB平面推进器多于3台，若其中p、q和j同时故障，式(6)减去式(12)得:

(26)

如果以上3台推进器不构成冗余关系，那么:

(27)

由式(26)导出式(27)时无约束条件，任意3台不构成冗余关系的推进器均满足式(27)，从而无法对故障推进器p、q和j进行准确定位。由于3台及以上推进器同时发生故障的概率通常较2台同时或者1台的低1个数量级以上，故可视为不会发生。

2.2.4 xBoByB平面故障推进器的定位算法

综上，可归纳出定位算法：

算法1：

记UUV在xBoByB平面配置了k台推进器，故障推进器的定位过程如下：

1) 当k=1时，由式(6)直接求出故障的加性描述，对比期望推力可实现故障推进器的定位。

2) 当k=2时，若无冗余，采用式(8)或(9)可求得故障的加性描述；若有冗余，基于定理1分析。

3) 当k=3时，若无冗余，采用式(11)求得故障的加性描述；若有冗余，基于定理1与2并参照(4)进行分析。

4) 当k>3时，基于定理1逐一分析是否存在某推进器满足式(15)，若满足则该推进器故障；无单推进器故障时，基于定理2逐对分析是否存在满足条件(25)的推进器组，若存在则该组推进器故障。

3 仿真分析

采用图3所示配置了4台推进器的UUV开展仿真验证，其控制矩阵为:

图3 配置4推进器的UUV俯视图

(28)

分析可知，该UUV任意3台推进器与第4台构成冗余关系。

为Th2和Th3分别设计故障:

(29)

(30)

仿真可得图4、图5所示的结果。

分析可知，在t∈[47,77)s阶段，图4(b)中三条曲线重合，满足约束(15)，表明Th2故障，与式(29)的设计相符。其后，图4中不存在三条曲线重合的情况，表明不是1台推进器故障。2台推进器同时故障的情形有6种，图5中实线表示故障估计所得模型控制输入的加性估计，余者表示经约束式(25)所得估计，从曲线重合情况可知，仅图5(a)中的组合(Th2,Th3)与实线完全重合，表明Th2与Th3同时发生故障，这与t≥s的实际情况相符。

图4 推进器故障的加性描述估计

图5 推进器组合满足约束式(25)的情况

经以上仿真实验，验证了本文所提定理与算法的有效性。

4 结论

本文针对UUV配置多台推进器的情况，研究了多台推进器故障的定位问题，采用几何相关性分析得出了配置于同一平面推进器的故障定位定理与算法，并获得了定位单台与2台推进器同时故障的约束条件，经仿真实验验证了所提定理与算法的有效性。

[1] Mangoubi R, Appleby B, Verghese G,et al. A robust failure detection and isolation algorithm[A].34th IEEE Conference on Decision and Control[C]. New Orleans, LA, USA: IEEE, 1995: 2377-2382.

[2] Alessandri, Caccia M, Veruggio G. Fault detection of actuator faults in unmanned underwater vehicles[J]. Control Engineering Practice, 1999, 7(3): 357-368.

[3] Corradini M, Orlando G. Actuator failure identification and compensation through sliding modes[J]. IEEE Transactions on Control Systems Technology, 2007, 15(1): 184-190.

[4] Corradini M, Monteriu A, Orlando G. An actuator failure tolerant control scheme for an underwater remotely operated vehicle[J]. IEEE Transactions on Control Systems Technology, 2011, 19(5): 1036-1046.

[5] Corradini M, Orlando G. A robust observer-based fault tolerant control scheme for underwater vehicles[J]. Journal of Dynamic Systems, Measurement, and Control, 2014, 136(3): 1-11.

[6] Omerdic E, Roberts G. Thruster fault diagnosis and accommodation for open-frame underwater vehicles[J]. Control Engineering Practice, 2004, 12(12): 1575-1598.

[7] Cristofaro, Johansen T. Fault tolerant control allocation using unknown input observers[J]. Automatica, 2014, 50(7): 1891-1897.

[8] Subsea World News. ROV Used for Dam Surveys[DB/OL]. 2015-08-19/2015-12-22. http://subseaworldnews.com/2015/08/19/rov-used-for-dam-surveys/.

[9] Fossen T. Guidance and control of ocean vehicles [M]. New York: John Wiley & Sons, Inc., 1994.

[10] 刘富樯,徐德民,高 剑,等.水下航行器执行机构的故障诊断与容错控制[J].控制理论与应用,2014,31(9):1143-1150.

Fault Location for Multiple Thrusters of Unmanned Underwater Vehicles

Liao Wenxian1, Huang Xingli2, Liu Fuqiang3

(1.College of information and communications, Zhejiang Industry&Trade Vocational College , Wenzhou 325003, China； 2.School of Automation, Northwestern Polytechnical University, Xi′an 710072, China； 3.College of Mechanical Engineering, Chongqing University, Chongqing 400044, China)

To assure the sailing safety of the Unmanned Underwater Vehicle (UUV) while operating under the complex sea, and reduce the tasks that come from the actuator faults, this paper investigates the Fault Location (FL) problem of the multiple actuators for the fault-tolerant control and thus improve the fault-tolerant capability of the UUV. The additive fault factors are estimated by following the given linear estimation algorithm based on the UUV nonlinear dynamics model; the geometric-correlation-based method is adopted to analyze the fault location (FL) problem for the multiple thrusters, where an FL algorithm together with the constraint conditions for FL is designed for the thrusters in the same surface; by combining the estimated fault factors with the constraint conditions, the fault situation is obtained under the proposed algorithm. Simulation experiment was constructed and verified the effectiveness of the proposed algorithm since the faulty actuator had been accurately located based on the proposed algorithm.

unmanned underwater vehicle (UUV); thruster; fault location (FL); redundancy

2016-07-01；

2016-07-22。

浙江省自然科学基金(LY14F020030)。

廖文献(1980-)，男，浙江温州人，硕士，讲师，主要从事自动化控制，图形图像处理方向的研究。

1671-4598(2016)12-0041-04

10.16526/j.cnki.11-4762/tp.2016.12.012

TP273

A