问题顺流而下 探究逆流而上
吴湘芸
(江苏省宜兴市丁蜀高级中学,214221)
问题顺流而下 探究逆流而上
吴湘芸
(江苏省宜兴市丁蜀高级中学,214221)
本文通过课堂实例,让学生认真参与发现问题、提出问题、分析问题、解决问题的过程,在每一个环节培养数学核心素养,从有效探究中拥有深层收获.
一、问题的引发
爱因斯坦说过,提出一个问题往往比解决一个问题更重要,因为解决一个问题也许仅仅是一个数学上的或试验上的技能而已,而提出新的问题、新的可能性,从新的角度看旧的问题,却需要创造.教学中要重视学生发现问题和提出问题能力的培养.
1.发现问题
用心思考才能发现有价值的问题.课堂中留给学生足够时间,给学生自主探索的机会,让学生自己发现或引导学生发现问题,仔细观察,大胆猜想.
例如,学习“两个平面垂直的判定定理”时,让学生阅读课本,学生会很自然地想知道下面这些问题:①两个平面垂直的定义是什么?②两个平面垂直有什么特点?③平面垂直的二面角如何做出?④如何判断两个平面互相垂直?
学生带着问题去阅读,顺着书本步步深入,不断产生新的疑问,想法设法去解答.学生对于自己设置的问题,会产生明确的学习目标,集中注意力,更感兴趣去探究,更能调动学习积极性.学生完全可以通过自主阅读找到知识主干,再通过对问题的研究拓展分支,而教师可在其基础上确定主方向.
在题目的解答过程中,允许错误的存在,但是最好从错误中找到原因,并能吸取教训.在批改过程中帮助学生把可能出现的错误归类,从错误中找出问题,探究出解题方法,也是可以提升解题能力的.
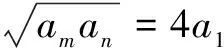
学生刚开始做这道题的时候经常犯同一个错误,为了加深他们的印象,可以让他们自己寻找错误原因,发现问题.学生们相互讨论,一开始都觉得自己做得很对,由已知条件得到结论:m+n=6,然后用“1”的代换,用基本不等式完成:
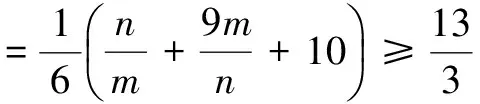
现在知道出现错误,那么问题在哪里呢?终于有学生指出,在用基本不等式时当且仅当n=3m时取等号,但此时m,n不是正整数.
针对发现的问题,由于是学生自己主动参与,一定会加深记忆,激发思维,增强学习积极性,又获得成功感.
2.提出问题
教师在课前仔细阅读教学参考书,查阅有关资料,根据教学需要形成教学情境,精心设计一部分问题,让问题呈现层次性,有适当梯度,慢慢铺垫,渐渐深化.学生的思维层层递进,感觉到通过努力就能接近成功,但不是一蹴而就,而是脚踏实地逐渐展开.
例如,复习“直线和圆的位置关系”时,设置问题:①直线与圆有几种位置关系?②这些关系判断方法分别是什么?③当直线与圆相离时,过直线上一点可作圆的几条切线?④当直线与圆相交时,弦长与弦方程的求法如何?⑤当直线与圆相切时,如何求切线长和切线方程?⑥过圆C外一点P引圆的切线,切点分别为A、B,切点弦方程是什么?P为动点时,如何求切线的最值?
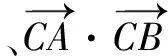
例2 已知m∈{x|ex-1+x-2=0},n∈{x|x2-ax-a+3=0},且存在m,n使|m-n|≤1,则实数a的取值范围是______.
由于此题学生出现错误较多,课堂上改变教师直接讲解的做法,让学生逐步提问,找到薄弱点.
师:大家读题后想到了什么?准备从哪里入手?
生1:题目没看懂,不知如何开始.
生2:有两变量m,n,都不会求.
生3:我觉得应该先求m,但是不会解方程,零点怎么求?
生4:我看出来了,m=1.可以猜出来,但具体怎么求解呢?
师:可以发现这个函数f(x)=ex-1+x-2单调递增,零点为x=1.
生5:条件变为|n-1|≤1,求出0≤n≤2,得出函数g(x)=x2-ax-a+3的零点的取值范围,接下去怎么求实数a的取值范围呢?
生6:可以画出抛物线图象,列式求解.
师:还有别的解法吗?
生7:也可变形为
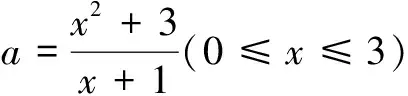
转化为求值域的问题.
学生们积极发言,不断有新的问题提出,然后大家想办法解决.学生提出的问题大多按照自己想法,符合实际需求,反映出自己的困扰,听到别人的想法,采纳不同的观点,拓宽解题思路,应该是非常受益的.
教师要鼓励学生提出问题,可以有单独提问、小组讨论、全班参与等多种方式,放手让学生自主学习,发挥想象,引发探索,深层探究.学生提出的问题与教师预设的问题会有差异,不时产生新想法,这很正常,让不同观念碰撞.教师启发诱导,在课堂中随时调整.
二、问题的探究
1.分析问题
形式多样,可以自主或合作探究,独立或讨论分析问题.讨论不是流于形式,而是真实需要.团队合作在于大家各取所长,能更快更好地解决问题,节约时间,提高效益.在与同学的交流中,感受各种思路和观点,又能增进感情.听其他同学对于问题的处理方法与观点,进行争论与比较,实际上对自己以后的解题会有很大的帮助.教师及时指导,鼓励学生勇于、善于表达自己观点,全体参与.实事求是地进行评价,肯定对的部分,以提问的方式指出其不足之处,留有足够思考的时间让学生调动思维,使他们真正成为探究的主体.当学生没有思路的时候,教师指导学生运用所学知识应用于解题.当学生的想法有偏离时,再引导他们回归正确的方向,起到督促导向的作用.
例3 平面直角坐标系中,已知平面区域
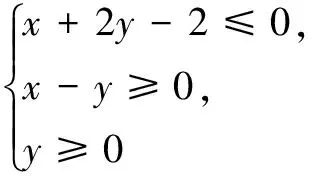
恰好被面积最小的⊙C及其内部所覆盖,则⊙C的方程是______.
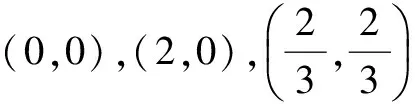
生2:我的解法和他相同,应该是正确的.
师:有不同意见么?
(这时做对的学生很积极地举手,想表达观点)
生3质疑:这种解法不对,外接圆并不是覆盖三角形的面积最小的圆.
生3解法:仔细观察图形,发现面积最小的圆是以(0,0),(2,0)为直径端点的圆.
生1总结:直观地认为是外接圆,没有仔细观察,深入思考.
2.解决问题
当遇到问题时,联想学过的知识点,以及相似的题型,寻找解法,由难化易,由繁化简,由复杂化简单,归纳规律方法,为以后解答问题积累经验.学生对参与这一过程非常有兴趣,而且对探究的结果很有信心.在脑海中形成同一类题目解题的方法.在课堂的最后对探究的过程、结果加以高度概括,编织知识网,变得系统化,形成深度学习,如果留有尚未详尽的部分或者学生特别感兴趣的部分,鼓励学生在课后加以研究,形成研究性学习报告或撰写小论文,与同学或教师探讨.
例如,通过试卷批改,教师发现学生对一类问题的解答总是出现各种问题,正确率不太高.准备在课堂上让学生探讨解决一类问题的解法并做好归类.
例4 已知f(x)=log2(x-2),f(m)+f(2n)=3,则m+n的最小值是______.
生1:先由f(m)+f(2n)=3,化简log2(m-2)+log2(2n-2)=3(m-2>0,n-1>0),得到
师:上面的解答过程详尽而完整.我们再深入地思考一下上面的解题过程,其中有整体代换的思想,同学们在解题的时候把m-2和n-1分别当成了一个整体来看待.所以我们是不是可以考虑用换元法试试看.
生2:我在解题时没有注意整体思想,而且运用基本不等式时很少验证等号何时取得.
生3:令m-2=a>0,n-1=b>0,则m=a+2,n=b+1,这题变成了:
已知a>0,b>0,ab=4,求a+b+3的最小值.
生4:这样一改变,变成了非常简单的题目,每位同学都会做了.
生5:令2a+b=x,b+1=y,那么
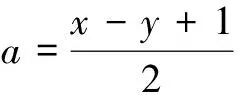
b=y-1,
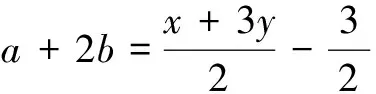
生7:通过简单的换元,追溯到最基本的解答方法,应用基本不等式解决问题.
例如,在数列这章里,在学习到“等差数列的前n项和”时,书本上有一道例题,提到了教育储蓄;在学习到“等比数列的前n项和”时,书上也有一道例题,提及公积金贷款.前者存款按单利计算,后者分期付款每期利息按复利计算.这些例子都十分贴近生活,学生们家中很多会有储蓄存款或借贷,他们在看到例题时就表现得很感兴趣,想弄清原理,如何计算,有何区别,等等.学生的问题很多,所以以此为课题组成小组去研究,写下他们的研究成果和探讨内容,一周一次与教师沟通后,继续整理,然后在课堂上选取代表向其余同学展示研究结果.
生活就是数学,学习数学的最终目的是解决问题.有的时候,数学教师之间连基本的“年化收益率”可能都不太清楚,这个不是因为太高深,而是最终解决问题的落脚点要找对、找准.在教学中,教师要帮助学生去探究、去思考、去提问、再掌握,这才是问题的解决.
三、习惯的培养
教师要着力创建自由、体验、探究、合作的平台,营造轻松愉快的学习氛围,发挥学生的主观能动性,使学生敢于提问、善于提问、有效提问,找出问题的本质;用数学的眼光观察问题,用数学的思维分析问题,用数学的语言表达问题.让学生通过实践对数学产生浓厚兴趣,让学生享受数学.
习惯的养成是一种潜移默化的过程,教师要在细节上对学生进行引导:第一次学生可能提出一个与现在的问题有关、甚至早已解决的问题,教师要学会接受并鼓励;下一次学生还会可能提出一个与之相同的问题,仅仅是形式稍有不同,也要赞赏他们的进步;再下次学生就很可能提出较新颖的问题,更要鼓掌表扬.在鼓励的同时,还要注重适时引导:看着未知数,还能不能试想出一个具有相同未知数或相似未知数的熟悉的问题?能否改变条件或结论?请用学过的知识点思考,能不能用不同的语句重新叙述问题?在这个方面,你能不能提出一个更容易着手的有关问题?仔细再想想,我们能不能提出一个更普遍的问题?假设你是出题的老师,你能不能提出一个更特殊、更深层的问题?你能不能提出一个类比的问题?你能否解决这个问题的一部分?保持了这样的引导和鼓励,加上逐步深入,有条理、有概括、有归类、有类比、有总结,这样学生的提问习惯有可能会被激发,探究自然顺势而为,数学提问的习惯也会逐步养成.
当然,习惯的养成也不是一蹴而就的.建立的主体是学生,要让学生在平时学习中及时提问,需要学生在课前加强预习,在课后及时总结巩固,在解题前强化审题,在错题中总结提炼,在思考中升华提升.这些更需要家庭的沟通教育,需要来自家长的鼓励和赞许.
总之,提问习惯的培养,不是简单地解决数学问题,更是对学生的一种人文关怀.孟子也“日省三身”;陶行知也有这个习惯,每天问自己三个问题:“今天我的学识进步了多少”、“今天我的品德进步了多少”、“今天我的健康进步了多少”.在学生今后的人生道路上,他们也需要时刻问一下自己,才能立于不败之地.
教师应该在数学课堂中培养学生问题意识,使学生养成提问、质疑的习惯,让探究成为常态,培养学生发现问题、提出问题、分析问题、解决问题的能力,从对问题的有效探究的过程中获得对知识的真正的深度理解,提高数学核心素养.

