基于ARIMA模型的贵阳市云岩区手足口病预测分析

李曦 温建 潘春柳 张江萍

(1.贵州医科大学公共卫生学院,贵州 贵阳 550004;2.贵阳市云岩区疾病病预防控制中心疾病预防控制科,贵州 贵阳 550004;3.贵阳市云岩区卫生与计划生育委员会,贵州 贵阳 550004)



·预防医学·

基于ARIMA模型的贵阳市云岩区手足口病预测分析

李曦1*温建2潘春柳2张江萍3△

(1.贵州医科大学公共卫生学院,贵州 贵阳 550004;2.贵阳市云岩区疾病病预防控制中心疾病预防控制科,贵州 贵阳 550004;3.贵阳市云岩区卫生与计划生育委员会,贵州 贵阳 550004)

手足口病; ARIMA; 趋势预测

手足口病(HFMD) 是婴幼儿常见的急性传染性疾病,多发生于5 岁以下的儿童,主要症状为手足口等多个部位出现疱疹,少数患者可发生严重的神经系统并发症如无菌性脑膜炎、脊髓炎等,甚至会导致患儿死亡[1]。该病主要由多种肠道病毒(EV) 引起,国内最常见的病原体是肠道病毒71 型(EV71) 和柯萨奇病毒A 组16 型(CoxA16)。根据2008-2014 年贵阳市云岩区手足口病的发病率，创建未来6年的发病预测数学模型，为制定手足口病的防控措施提供科学依据。

1 资料和方法

1.1 资料来源 研究数据来源于《中国疾病预防控制信息系统》中贵阳市云岩区2008-2014年疫情监测数据。

1.2 方法

1.2.1 ARIMA模型建模原理 将预测对象随时间推移而形成的数据序列视为一个随机序列,用一定的数学模型来近似描述这个序列。这个模型一旦被识别后就可以从时间序列的过去值及现在值来预测未来值。根据原始数据序列是否为平稳,模型可以分为:季节性ARIMA(p,d,q)(P,D,Q)S和非季节性ARIMA(p,d,q)[2],其中ARIMA(p,d,q)称为差分自回归移动平均模型,AR是自回归, p为自回归项; MA为移动平均,q为移动平均项数,d为时间序列成为平稳时所做的差分次数。

1.2.2 建模的方法和步骤 ARIMA建模法分为三个阶段:模型识别、参数估计和诊断检验、预测[3]。模型识别阶段:对贵阳市云岩区2008-2014年的手足口病发病率进行“日期定义”,绘制贵阳市云岩区手足口病发病率原始和差分后的自相关系数图(ACF)和偏相关系数图(PACF),以ADF单位根检验其方差、趋势及其非季节性变化规律,对序列的平稳性进行识别。参数估计和诊断检验阶段:显著性检验可以确定是否需要模型中的一些项,拟合优度的统计量可以确定模型拟合的优劣程度;运用Akaike信息标准(AIC)和Schwartz Bayesian标准(BIC)作为模型选择准则,其中参数值小者为优。预测阶段:利用云岩区2008-2014年发病率创建的模型,预测贵阳市云岩区2008-2020年手足口病发病率。

1.3 实现软件 用EXCEL对原始数据进行分类整理,使用SPSS 19.0进行ARIMA模型进行创建,检验水准α=0.05。

2 结 果

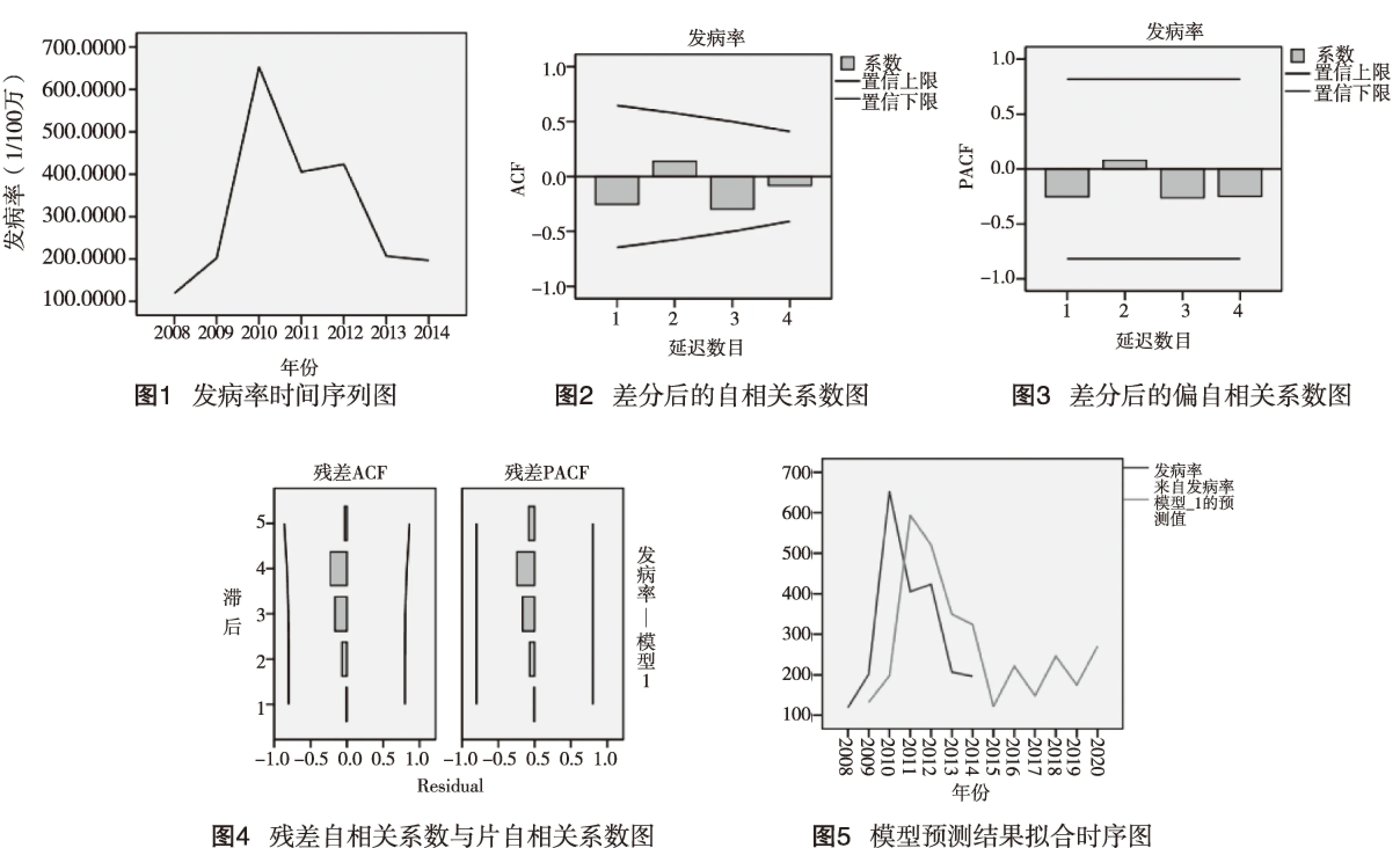
2.1 创建平稳序列 绘制2008-2014年的手足口病发病率时间序列图(图1)。由图1可知云岩区2008-2014年的手足口病发病率为非平稳序列,无明显季节性,对原始时间序列进行一阶差分后近似平稳序列。

2.2 模型识别 为使时间序列平稳,先将云岩区手足口病发病率进行差分,差分后的自相关系数图2(ACF)和偏相关系数图3(PACF),该序列通过一阶非季节性差分可以达到近似平稳序列,此时,可创建ARIMA模型。

2.3 参数估计和诊断检验 由时间序一阶列差分得到类似平稳序列，可得出d=1;由ACF图(图2)，出现滞后现象Lag=1，q=1; 由PACF图(图3), 出现滞后现象Lag=1，p=1。因模型阶数过高会造成过度拟合，故各阶数均限定在2以内，SPSS19.0报告得出的最终参数：平稳的决定系数，同时应用Akaike信息标准(AIC)和Schwartz Bayesian标准(BIC)作为模型选择准则。根据SPSS 19.0 报告的拟合优度和统计量结果可见，排除与预测结果差异太大的模型ARIMA(1,0,1)和ARIMA(0,1,1)，两个较好的备选模型中ARIMA(1,1,1)，ARIMA(1,1,0)相比较，模型ARIMA(1,1,1)的AIC11.570、BIC11.462及残差方差均小，而其参数的P<0.05，选定该模型建立方程。

对ARIMA(1,1,1)的残差做自相关和偏自相关分析(图4)残差是随机的白噪声，残差序列的box-ljung Q统计结果显示统计量差异均无统计学意义(P>0.05)，对残差序列进行t 检验，差异无统计学意义(P>0.05)。进一步证实残差是白噪声序列，所选模型恰当。

2.4 预测结果 根据已知的贵阳市云岩区2008-2014年手足口病发病率(1/10万)，运用ARIMA(1,1,1)模型对贵阳市云岩区2015-2020年手足口病发病率(1/10万)进行预测，预测结果依次为121.1742、221.1876、148.1587、245.9970、175.0109、270.7259。拟合时序图如下(图7)。经检验预测结果拟合度较好，由图5可见，拟合时间序列动态趋势与真实时间序列动态趋势基本一致；拟合结果都在预测发病率的95%可信限(95%CI)。由ARIMA(1，1，1)模型参数结果可得出预测模型为：Dyt=yt-yt1；Dyt=-0.990Dyt-1+εt+εt-1。

3 讨 论

随着数学模型被运用到交叉学科以来,运用数学模型进行预测,运用数理统计来寻求事物规律思维的发展与完善,越来越多的数学理论、统计方法及预测模型被应用于传染病的预测。但是,我们并不能用单一因素分析传染病的流行特征及规律,应从传染病的发病特征,发病人群,发病时间,发病因素等等水平来预测传染病。ARIMA 预测模型是基于原始数据服从时间序列分布,利用任何事物发展均具有一定惯性趋势的原理,建立时间序列模型,从而达到预测的目的[4]。ARIMA 预测模型既吸收了传统回归分析的优点又发挥了移动平均的长处,具有适用范围广,实用性强、预测误差小的特点,是 一种预测精确度较高的短期预测方法[5]。

本研究对2008-2014年云岩区手足口病发病情况,运用ARIMA(1,1,1)模型通过模型识别、参数估计和诊断检验、预测三个阶段完成数学建模。模型预测的结果均在95%CI内,预测结果显示未来6年贵阳市云岩区手足口病的发病不会持续下降,相反发病率会出现反复状态。因此,这就需要相关部门提前预警,加大防控工作力度,防止手足口病出现大规模流行。

数据记录的准确性和全面性对数学模型的预测至关重要。因此 为提高模型预测的准确度和精度,应全面收集影响传染病发生的相关因素,建立可以考虑到影响因素的预测模型[6]。在今后传染病监测和预防工作中,首先应提高传染病的报告准确性和记录全面性;其次要运用预测模型结果,运用不断更新的数据多次拟合预测未来发病率,谨慎使用传染病预测结果,提前引导社区居民,易感人群做好消毒和防护措施,为工作人员采取预防措施提供正确的参考依据,以期最大化实现控制疾病的传播。

[1] 张雅娟, 崔彩岩, 史刘辉. 2010-2013年西安市手足口病流行病学特征分析[J]. 现代预防医学, 2015,42(7):1235.

[2] 范引光, 吕金伟, 戴色莺,等. ARIMA模型与灰色预测模型GM(1,1)在HIV感染人数预测中的应用[J]. 中华疾病控制杂志, 2012, 16(12):1100-1103.

[3] 朱奕奕, 冯玮, 赵琦,等. ARIMA乘积季节模型在上海市甲肝发病预测中的应用[J]. 复旦学报:医学版, 2012, 39(5):460-464.

[4] 谭姣,雷静 . ARIMA 模型在乙型病毒性肝炎发病率预测中的应用[J]. 公共卫生与预防医学,2013,24(4):8-10.

[5] 张泽武,卢展鹏,曾耀明,等. ARIMA 模型在东莞市细菌性痢 疾预测中的应用[J]. 公共卫生与预防医学,2013,24 (4) :43-45.

[6] 韩琴,苏虹,王忱诚,等. ARIMA 模型与GRNN 模型对性病发病率的预测研究 [J]. 现代预防医学,2012,39 (6) : 1337-1340.

R181.8

B

1000-744X(2016)07-0775-02

2016-03-03)

*贵州医科大学公共卫生学院2014级在读硕士研究生

△通信作者,E-mail:jpzhang1972@163.com