基于模糊PID的多类型轴同步运动控制技术研究
林辰龙,褚卫华,刘 念,盖 文
(中国空气动力研究与发展中心设备设计及测试技术研究所,四川绵阳 621000)
基于模糊PID的多类型轴同步运动控制技术研究
林辰龙,褚卫华,刘 念,盖 文
(中国空气动力研究与发展中心设备设计及测试技术研究所,四川绵阳 621000)
在风洞设备中,存在着大量多轴联动或同步运动驱动机构,多轴同步运动精度影响风洞试验的品质;为提高多轴同步运动精度,对常用的同步控制模型进行了研究和分析,提出了以模糊PID控制算法为核心的主-从式与耦合式相结合的控制模型,并开展了双电机轴系统、双液压轴系统以及混合轴系统的建模仿真与试验分析;试验结果表明该控制方法不仅能够减小多轴同步系统的同步运动误差,还能有效减小外部干扰的影响。
多轴系统;同步控制;同步误差;模糊PID控制
0 引言
在风洞设备中存在着大量的多轴运动机构,如柔壁系统、栅指机构、模型支撑机构等。这些机构大多由多个电机或多个液压伺服系统驱动,只有保证多个电机或油缸之间按某种比例关系同步协调运转,才能确保风洞试验的品质。因此,研究多轴系统的同步运动控制,提高其同步精度,对风洞试验具有重要的意义。
当前使用较多的同步控制模型大致上可分为3种,即主令参考式模型[1]、主-从式模型[2]和耦合式模型。主令参考式模型结构简单,但无法适应复杂的控制对象,特别是存在负载扰动时的同步控制。主-从式模型能够解决由于主轴的扰动引起的失同步问题,但无法解决从轴负载变化对同步性能的干扰,而且整体性能也被主轴的性能所制约。耦合式模型包括交叉耦合式模型[3]、偏差耦合式模型[4]以及虚拟主轴模型[5]等,其对干扰和负载的变化适应性最强,在同步控制系统中能取得最好的控制效果,但由于引入了轴间参数耦合,使模型在计算机中的实现非常复杂,而且还有可能导致系统整体稳定性变差。调研发现,目前同步控制的研究对象大多是多个电机间的同步[6 8],对多个油缸以及电机和油缸的混合同步研究较少。由于电液伺服系统的控制是非线性的,多个油缸以及电机和油缸的混合同步必然有别于多个电机的同步。
为此,本文在当前控制模型的基础上提出了一种以模糊PID控制为核心,主-从式模型和耦合式模型相结合的同步控制模型,并搭建了双电机轴试验系统、双液压轴试验系统和电机-液压混合轴试验系统,利用该试验系统进行了建模仿真和试验分析,验证了所提出的同步控制模型的有效性。
1 同步控制模型
同步控制模型如图1所示。首先定义一根虚拟运动轴,根据所给运动参数规划每一时刻的位移或速度,各个实际运动轴则跟随虚轴的速度或位移运动;然后在各个轴间设置耦合控制器,综合各个运动轴的实际位移或速度,根据跟随指令、自身的位移或速度反馈指令以及耦合控制器的指令计算得到各个轴的实际运动指令控制轴的运动。该同步控制策略包含了主-从同步控制策略和耦合同步控制策略两种同步控制策略的思想,能够解决主-从式模型受主轴性能制约的局限性和从轴负载变化的影响。
目前常用的虚拟轴路径规划曲线主要有两种:一种是梯形速度曲线,另一种是抛物线形速度曲线,图2所示。梯形速度曲线是在定加速度下启动,当速度达到要求时匀速运行,以一定值负加速度制动定位;而抛物线形速度曲线则是在变加速度下启动,保证启动过程速度平稳过渡,当速度达到要求时匀速运行,以变负加速度制动定位,保证制动定位过程速度平稳过渡。
耦合控制器的最直观的控制策略是:在运动过程中,根据各轴的运动情况找到一个平衡点,让比平衡点快的轴慢下来,同时使比平衡点慢的轴快一点,从而达到实时调整各轴运动的目的,减小同步误差。

图1 同步控制模型

图2 路径规划曲线
2 模糊PID控制器设计
模糊控制器具有鲁棒性好、动态特性佳的特点,但静态误差却难以消除。而PID控制器中的积分环节能很好地消除静态误差,但其动态响应效果差。因此可以将模糊控制和PID控制算法结合起来,两种算法取长补短,形成模糊PID控制算法,可以达到更好的控制效果[9]。
目前,模糊PID控制器已经被广泛应用。模糊PID控制器有多种形式[10],但它们的控制原理基本上都是一致的,即根据采样计算得到的误差和误差变化率,运用技术人员的经验得到的模糊推理规则,建立比例系数,微分系数,积分系数模糊控制表,进行控制。模糊PID控制器结构如图3所示。
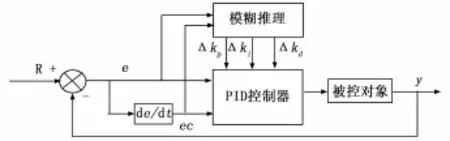
图3 模糊PID控制器
由图3可以看出,模糊PID控制器由模糊推理和PID控制器两部分组成,其中e,ec为控制器输入量,Δkp、Δki、Δkd为控制器输出量。模糊PID控制器就是在控制过程中不断检测偏差和偏差变化率,根据模糊控制规则,实时调整kp、ki、kd3个参数的值:


其中:k′p,k′i,k′d为初始参数。
2.1 系统输入输出变量
同步控制系统控制器的目的是减小同步误差,模糊PID控制器中PID控制器是模糊控制器校正的,因此控制器的输入量选为位移偏差e和偏差变化率ec,输出量选为PID控制器的比例系数kp,他们的语言变量分别为E、EC和Δkp。系统变量的论域根据系统的实际运动情况和控制精度进行选取。
选取“正大(PB)”、“正中(PM)”、“正小(PS)”、“零(Z)”、“负小(NS)”、“负中(NM)”、“负大(NB)”来描述系统变量。则得到系统模糊子集为:{NB,NM,NS,Z,PS,PM,PB}。各变量隶属函数均选择两边为高斯形隶属函数,中间为三角形隶属函数的组合函数形式。
2.2 模糊控制规则
模糊PID控制器就是不同时刻的输入量的组合与PID控制器参数之间的控制关系。系统运行时,根据不同的输入量组合,控制器根据控制规则给出PID控制器参数的变化量,达到好的控制效果。根据同步控制的特点,实时计算各轴位移的均值,位移偏差为该均值与被控轴位移的差值,得到模糊控制规则如表1所示。双轴系统可取位移偏差为轴1与轴2的差值,采用上表规则控制轴1,轴2的规则则恰好相反。
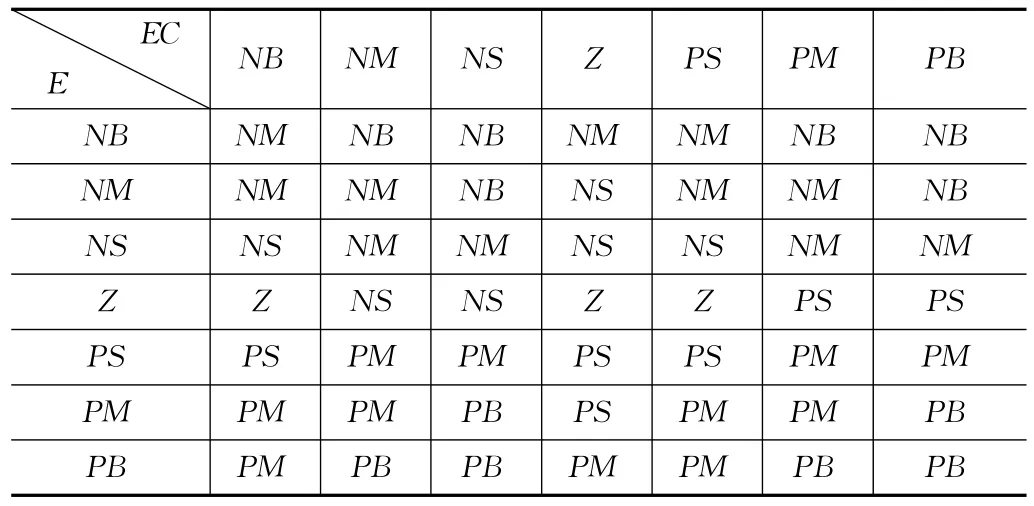
表1 模糊控制规则
2.3 解模糊化
采用面积中心法进行解模糊化。由得到的模糊控制规则,根据系统计算的偏差及偏差变化率可得系统的输出量。得到模糊控制器的输出量后再加上前一时刻的参数值即可实时改变控制器的参数。
3 建模与仿真分析
3.1 双电机轴系统建模与仿真分析
双电机轴系统采用两套伺服电机,在Lab VIEW平台上建立数学模型,如图4所示。
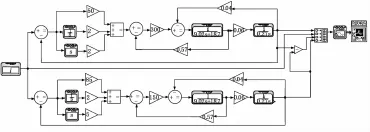
图4 双电机系统仿真模型
分别对两电机轴添加PID控制器,调整PID参数,得到的仿真结果如图5中的虚线所示,此时两轴的同步误差为0.020 85。利用本文提出的控制策略,添加模糊PID控制器,得到的仿真结果如图5中的实线所示,可以看出两轴的同步精度得到明显的提高,同步误差缩小到了0.004 139。

图5 双电机轴系统控制仿真
从以上的仿真结果可以看出,本文提出的控制策略是有效的,同步控制精度比只有传统PID控制器的情况下提高了80.14%。
3.2 双液压轴系统建模与仿真分析
双液压轴系统采用两套电液伺服系统,包括两个伺服阀和两个液压缸,在Lab VIEW平台上建立数学模型,如图6所示。
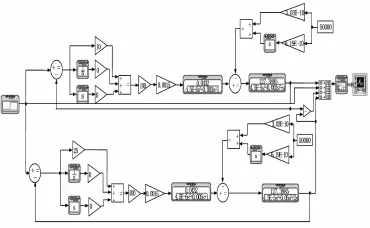
图6 双液压轴系统仿真模型
分别对两液压轴添加PID控制器,调整PID参数,得到的仿真结果如图7中的虚线所示,此时两轴的同步为0.125 3。利用本文提出的控制策略,添加模糊PID控制器,得到的仿真结果如图7中的实线所示,可以看出两轴的同步精度得到明显的提高,同步误差缩小到了0.099 63。

图7 双液压轴系统控制仿真
从以上的仿真结果可以看出,本文提出的控制策略是有效的,同步控制精度比只有PID控制器的情况下提高了20.5%。
3.3 电机-液压混合轴系统建模与仿真分析
电机-液压混合轴系统由双电机轴系统中的一套伺服电机和双液压轴系统中的一套电液伺服系统组成,在Lab VIEW平台上建立数学模型,如图8所示。

图8 电机-液压混合轴系统仿真模型
分别对两轴添加PID控制器,调整PID参数,得到的仿真结果如图9中的虚线所示,此时两轴的同步误差为0.139 3。利用本文提出的控制策略,添加模糊PID控制器,得到的仿真结果如图9中的实线所示,可以看出两轴的同步精度得到明显的提高,同步误差缩小到了0.088 19。

图9 双液压轴系统模糊PID控制仿真
从以上的仿真结果可以看出,本文提出的控制策略是有效的,同步控制精度比只有PID控制器的情况下提高了36.7%。
4 试验分析
4.1 双电机轴系统试验分析
双电机轴同步运动控制系统主要由NI CompactRIO 9068控制器,Kellmorgen AKM24D-ANCNDB00伺服电机和伺服电机驱动器AKD-P00306NBEC组成。各个模块之间通过EtherCAT通信协议进行数据传递。
在Lab VIEW环境下编写控制代码,设置两电机轴的PID参数,运行系统得到试验结果如图10所示。图中有四段曲线,分别代表PID控制、模糊PID控制、干扰条件下的PID控制和干扰条件下的模糊PID控制四种情况下的试验结果。
从以上试验结果可以看出,在PID控制情况下,两轴的同步误差为1.298 54 mm,在模糊PID控制情况下,两轴的同步误差缩小到0.349 5 mm,控制精度提高了73.1%;在存在干扰的PID控制情况下,两轴的同步误差为4.011 5 mm,在存在干扰的模糊PID控制情况下,两轴的同步误差缩小到0.404 35 mm,控制精度提高了89.9%,且与无干扰情况下的控制结果相近。由此证明本文提出的模糊PID控制策略能够有效提高双电机轴系统的同步控制精度,减小同步误差,并且能够有效降低干扰的影响。

图10 双电机轴同步误差
4.2 双液压轴系统试验分析
双液压轴试验系统液压部分由液压源、液压动力元件、位置传感器和负载机构组成。为模拟载荷变化,采用了两种负载机构,一种是简易杆支撑机构,另一种是定载荷机构。
在Lab VIEW环境下编写控制代码,设置两液压轴PID控制参数,得到PID控制情况下运动曲线,如图11中的虚线所示。由于简易杆支撑机构在运动过程中油缸负载随时间实时变化,因此两轴间的同步误差也实时变化。采用模糊PID控制,得到运动曲线如图11中的实线所示。

图11 双液压轴系统控制同步误差
从以上试验结果可以看出,只有PID控制的情况下的同步误差为4.826 71 mm。采用模糊PID控制后,同步误差降到了1.860 24 mm,精度提高了61.4%,误差控制在2 mm以内。由此可以证明本文提出的模糊PID控制策略能够有效提高双液压轴系统的同步控制精度,减小同步误差,并且能够有效降低干扰的影响。
4.3 电机-液压混合轴系统试验分析
电机-液压混合轴试验系统由双电机试验系统中的一根电机轴和双液压轴系统中的简易杆支撑机构组成。
在Lab VIEW环境下编写控制代码,设置两轴PID控制参数,得到PID控制情况下的运动曲线,如图12中的虚线所示。由于简易杆支撑机构在运动过程中油缸负载随时间实时变化,因此两轴间的同步误差也实时变化。采用模糊PID控制,得到运动曲线如图12中的实线所示。
从以上试验结果可以看出,只有PID控制的情况下的同步误差为41.082 4 mm。采用模糊PID控制后,同步误差降到了3.590 14 mm,误差控制在4 mm以内。由此可以证明本文提出的模糊PID控制策略能够有效提高混合轴系统的同步控制精度,减小同步误差,能够有效降低干扰的影响。

图12 电机-液压混合轴试验系统控制同步误差
5 结论
本文针对目前在实际生产中使用广泛的多轴系统的同步运动控制技术开展了研究,在总结常用同步控制模型优缺点的基础上,提出了一种以模糊PID控制器为核心的主-从式和耦合式模型相结合的控制模型,根据同步运动控制的特点选取了路径规划曲线以及模糊PID控制器的参数和规则,并分别在双电机轴试验系统、双液压轴试验系统和电机-液压混合轴试验系统中进行了建模仿真与试验分析,取得了预期的效果。结果表明本文提出的控制方法能够有效降低多轴系统的同步运动误差,并且能够有效应对干扰的影响。
[1]Valenzuela MAnibal,Lorenz R.Electronic line-shafting control for paper machine drives[J].IEEE Transactions on Industry Applications,2001.
[2]Shim HM,Hong J P,Chung S B.Powered wheelchair controller based on master-slave control architecture[A].IEEE International Symposium on industrial e1ectronics[C].2001.
[3]Koren Y.Cross-coupled biaxial computer control for manufacturing systems[J].ASME Journal of Dynamic Systems.Measurement and Control,1980.
[4]Perez-Pinal J,Calderon C,Araujo I.Relative Coupling Strategy [A].Proceeding of IEEE International Electric Machines and Drives Conference[C].Madison:IEEE,2003.
[5]Payette K.SynchronizedMotion Control With the Virtual Shaft Control Algorithm and Acceleration Feedback[A].Proceedings of the American Control conference[C].1999.
[6]孙 江.多电机同步协调控制系统的研究[D].太原:太原科技大学,2009.
[7]张 莉,李彦明,马陪荪,等.基于模糊PID控制器的多电机同步控制装置的应用[J].工业仪表与自动化装置,2003.
[8]吴其华.多电机虚拟总轴同步控制系统研究[D].武汉:华中科技大学,2003.
[9]Dong Peixin,Wang Qinruo,Tao Yu.The Application of Fuzzy PID Control in Aerosol Automatic Conference System[A].Proceeding of the fourth World Conference on Intelligent Control and Automation[C].2002.
[10]马俊功,王世富,王占林.电液速度伺服系统的模糊PI控制[J].控制工程,2006(11).
Research on Synchronization Motion Control Technology Based on Fuzzy PID for Multi-type axis System
Lin Chenlong,Chu Weihua,Liu Nian,Gai Wen
(Facility Design and Instrumentation Institute,China Aerodynamics Research and Development Center,Mianyang 621000,China)
There are a large number of multi-axis synchronization motion systems in the wind tunnels.The precision of synchronization motion affects the quality of wind tunnel test.In order to improve the synchronization motion precision of multi-axis system,the common synchronization control models were analyzed firstly.Then,a new control model which was based on the fuzzy PID control algorithm and the combination of master-slave model and coupling model was presented.At last,the simulation and test analysis of double-motor system,double-hydraulic system and mixed-axis system were done.The result showed that the control algorithm presented can efficacious decrease the motion error of multi-axis system and the influence of interference.
multi-axis system;synchronize control;synchronize error;fuzzy PID control
1671-4598(2016)08-0099-04
10.16526/j.cnki.11-4762/tp.2016.08.027
:TP27
:A
2016-02-26;
:2016-04-11。
林辰龙(1990-),男,福建莆田人,助理工程师,主要从事流体传动与控制、控制系统方向的研究。

