基于广度优先搜索算法的故障隔离矩阵生成方法
张延生,乔中涛,井建辉
(军械工程学院导弹工程系,石家庄 050003)
基于广度优先搜索算法的故障隔离矩阵生成方法
张延生,乔中涛,井建辉
(军械工程学院导弹工程系,石家庄 050003)
相关性矩阵表示故障与测试之间的逻辑关系;隔离矩阵表示在给定的测试顺序下,故障隔离与测试之间的需求关系;测试顺序对诊断费用影响可以通过隔离矩阵进行计算;所以求解隔离矩阵是诊断费用优化的前提;针对相关性矩阵与隔离矩阵易于混淆的问题,以及传统分析方法求解隔离的不足,详述隔离矩阵的概念和生成原理,设计基于广度优先搜索的隔离矩阵生成算法;示例表明,生成算法是可行的和有效的。
测试性;隔离矩阵;广度优先搜索算法
0 引言
随着测试诊断费用在武器装备全寿命周期费用中所占比例不断提高,测试性研究也越来越受到重视。测试性作为系统的重要设计特性之一,描述的是系统的故障检测和隔离能力[1]。把故障定位到实施修理时可更换的单元的过程称为故障隔离。故障诊断隔离费用与系统状态概率、测试费用和测试顺序密切相关。测试顺序对诊断费用的影响可用故障隔离矩阵表示。设系统故障隔离需要n个测试,对应的测试顺序有n!个。在系统状态概率和测试费用确定后,诊断费用的优化就是在n!个测试顺序中寻找最优的测试顺序,使系统故障诊断隔离费用最低。一些文献在计算最优诊断费用时,用到隔离矩阵,但就隔离矩阵概念和生成方法没有详述[2-3]。有些文献甚至将故障隔离矩阵与故障测试相关性矩阵混淆,错误地将相关性矩阵代替隔离矩阵进行优化计算[4]。因此,准确地求解测试顺序对应的故障隔离矩阵就显得十分必要。
1 故障测试相关性矩阵
建立故障与测试之间联系是进行故障诊断的基础。故障与测试之间的关系可用故障测试相关性矩阵D=[dij](m+1)×n表示,如式(1)所示。其中,F0表示系统无故障状态,Fi(i=1,2,…,m)表示系统的组成单元,tj(j=1,2,…,n)表示测试。如果dij=1表示Fi单元发生故障时,tj能够测得,即Fi与tj相关;如果dij=0表示Fi单元发生故障时,tj不能够测得,即Fi与tj无关[1]。


图1某雷达频综系统功能结构图
图1 为某雷达频综系统的功能结构图,F1、F2、…、F9为组成单元,T1、T2、…、T9为测试。它的相关性矩阵如式(2)所示。其中,C=[C1,C2,…,Cn]1×n为测试费用向量。测试Tj(j =1,2,…,n)的费用为Cj,包括了测试时间、测试硬件软件消耗、测试人力消耗等费用。P=[P0,P1,P2,…,Pm]1×(m+1)为状态概率向量。系统处于状态Fi(i=0,1,2,…,m)时,对应的状态概率为Pi,且满足。

2 诊断推理与测试响应矩阵
在相关性矩阵基础上,可以进行故障诊断。诊断推理过程是在以下假设下进行:
1)当系统发生故障时,认为只有一个单元发生故障;
2)测试结果准确可靠,测试结果只有通过和不通过两种情况,分别用逻辑“0”和“1”表示,且任何两个测试之间是相互独立的。
设在测试顺序T1、T2、…、Tn下,根据测试结果,得到测试响应向量R=[x1,x2,…,xn],其中xi∈{0,1}且i=1,2,…,n。在相关性矩阵基础上,根据测试响应向量R确定故障过程即为诊断推理过程。例如,如果响应向量R1=[0,1,X,X,X,X,X,X,X],其中X表示0或1,它的取值不影响诊断推理的结果,诊断推理的过程可用图2表示。当T1=0时,根据相关性矩阵D,系统状态是模糊组[F0、F2、F3、F4、F5、F6、F7、F8、F9];当T2=1时,由相关性矩阵D,可判断是F2发生故障。系统的任何单元发生故障时,都会有相应的测试响应向量和诊断推理图,将所有测试响应向量放在一起就构成了响应矩阵,将所有诊断推理图画在一起就形成了诊断树。本例中测试响应矩阵和诊断树分别如式(3)和图3所示。

图2 测试响应R1诊断推理过程
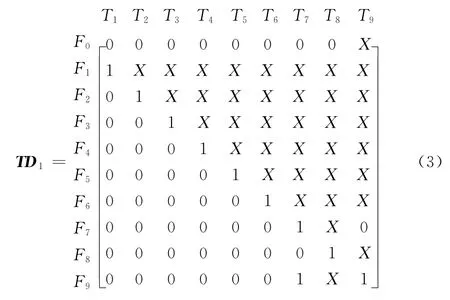

图3 测试顺序T1、T2、…、Tn下的诊断树
3 故障隔离矩阵
图3诊断推理过程和式(3)响应矩阵是在测试顺序T1、T2、T3、T4、T5、T6、T7、T8、T9得到的。那么改变测试顺序,诊断推理过程和响应矩阵也将改变。仍以图1为例,测试顺序变为T8、T9、T7、T3、T4、T5、T6、T1,诊断推理过程则如图4所示,响应矩阵如式(4)所示。
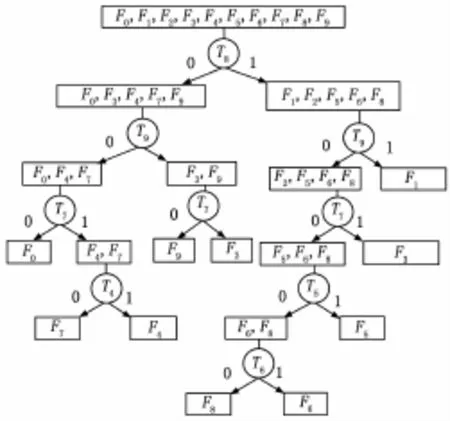
图4 测试顺序T8、T9、T7、T3、T4、T5、T6、T1下的诊断树

比较响应矩阵式(3)和式(4)可知,在不同测试顺序下,响应矩阵是不同的。对于F0而言,在测试顺序T1、T2、T3、T4、T5、T6、T7、T8、T9下,用到了所有的测试,才能确定是F0状态;而在T8、T9、T7、T3、T4、T5、T6、T1下,只用到了T8、T9、T7三个测试,就可以确定。对于其他状态也类似,即在不同测试顺序下,确定系统状态所使用的测试个数存在差异。确定状态Fi(i=0,1,2,…,m)时所需要测试可以用隔离向量Ii=[bi1,bi2,…,bin]表示,其中bij∈{0,1}。bij=1表示确定状态Fi时,用到了测试Tj;bij=0表示确定状态Fi时,没有用到测试Tj。例如,在测试T1、T2、T3、T4、T5、T6、T7、T8、T9下,T7的隔离向量为I7=[111111101],在T8、T9、T7、T3、T4、T5、T6、T1下,为I7= [000100111]。
将所有状态的隔离向量放在一起就构成了隔离矩阵。系统的隔离矩阵用I=[bij](m+1)×n表示,即式(5)所示。隔离矩阵物理意义表示在给定测试顺序下进行故障诊断推理,故障隔离到各个单元时,所用的测试。
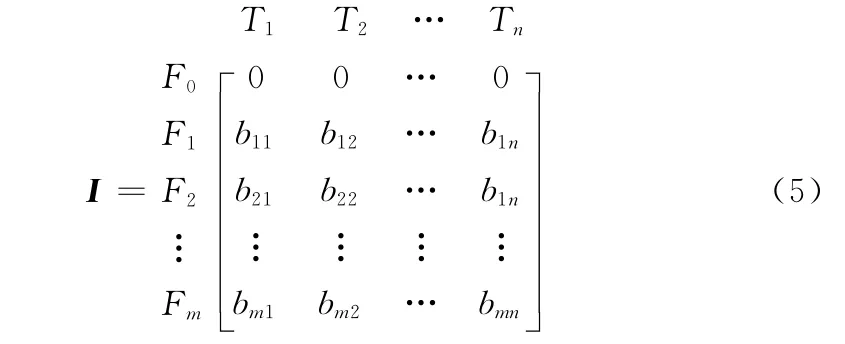
T1、T2、T3、T4、T5、T6、T7、T8、T9测试顺序下的故障隔离矩阵I1如式(6)所示。

T8、T9、T7、T3、T4、T5、T6、T1测试顺序下的故障隔离矩阵I2如式(7)所示。

4 故障隔离矩阵对诊断费用的影响
诊断费用是指在系统相关性矩阵和给定的测试顺序下,确定系统状态所需总的平均测试费用CZ。

其中:C=[C1,C2,…,Cn]1×n为测试费用向量。P=[P0,P1,P2,…,Pm]1×(m+1)为状态概率向量。I=[bij](m+1)×n为故障隔离矩阵。
式(8)中,系统的状态概率向量P通常是不变的;所选测试一旦确定以后,它的费用向量C也是不变的;而故障隔离矩阵I随测试顺序改变而改变,直接影响着测试费用CZ。例如在测试顺序T1、T2、T3、T4、T5、T6、T7、T8、T9和T8、T9、T7、T3、T4、T5、T6、T1情况下总测试费用分别为CZ1和CZ2,如式(9)、(10)所示。可见,测试顺序的不同,隔离矩阵也将不同,导致总测试费用也不同。为了寻找最低费用的测试顺序,需要遍历所有测试顺序下故障隔离矩阵。依靠传统的分析方法获取隔离矩阵,既不现实也不可能,如何自动生成故障隔离矩阵就变得非常必要。

5 隔离矩阵生成原理
隔离矩阵求解过程,就是用测试T(1)、T(2)、…、T(n-1)、T(n)不断对系统状态F=[F0,F1,F2,…,Fm]分割的过程,每次分割都将产生新的模糊组,然后继续用其它测试再对新的模糊组进行分割,分割的过程不断循环,直至隔离到单个故障,或所有测试均用完为止[5],记录下分割标记,就可得到隔离矩阵。
设该系统的初始状态为模糊组R0=[F0,F1,F2,…,Fm]。通过一组测试对模糊组R0逐渐分割,直到分割为单个状态Fi(i=0,1,2,…,m)。不妨用测试顺序为T1,T2,…,Tn的测试进行分割,且模糊组R0经过T1、T2、…、Tk-1分割后,当前的模糊组为Rp,Rp+1,…,Rp+q,下一步要用Tk进行分割。根据相关性矩阵,与Tk相关的模糊组(Tk可以检测到的故障)为:

与Tk无关的模糊组为:
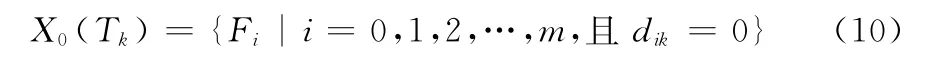
当用Tk对模糊组为Rp,Rp+1,…,Rp+q分割时,有两种结果,一种是Tk通过,其逻辑值为“0”,说明与Tk无关的系统状态被分割出;另一种结果是Tk没通过,其逻辑值为“1”,说明与Tk相关的系统状态被分割出。设对Rp分割出的模糊组为Rp+q+1和Rp+q+2,即:

当前系统状态模糊组Rp,Rp+1,…,Rp+q被Tk分割完成后,分割结果即系统的状态模糊组为:Rp+q+1,Rp+q+2,…,Rp+q+(2q+1),Rp+q+(2q+2)。
在分割出的模糊组中,某个模糊组Rp+q+2i(1≤i≤q)可能存在以下几种情况。
1)Rp+q+2i或Rp+q+(2i+1)是已经分割为单个状态Fi(i=0,1,2,…,m),该状态Fi路径到此为止;
2)Rp+q+2i=Ø且Rp+q+(2i+1)=Rp+q+i,表明Tk没有对父辈模糊组Rp+q+i进行分割;
3)Rp+q+2i或Rp+q+(2i+1)仍然包含多个状态,继续用Tk+1进行分割。
当所有模糊组仅包含有一个状态时,或者所有测试都已用完,则分割过程结束。此时,记录下每个状态所用到的测试,且该测试确实对状态路径中的模糊组进行了分割,即可得到该状态的隔离向量。所有状态的隔离向量即可构成隔离矩阵。
6 隔离矩阵生成算法
依据隔离矩阵的生成原理,采用广度优先搜索算法[6]。首先把初始模糊组作为当前状态,调用分割子程序对其进行分割,生成一组新的模糊组。按照广度优先搜索原则依次将这些状态存入到OPEN表中。然后从OPEN表中取出下一状态作为当前状态,继续调用分割子程序,直到分割到单个单元,或所有测试已用完为止。
1)分割子程序:诊断树生成过程也可以认为是用测试对模糊组不断的分割过程,诊断树枝上的每个节点就是一次分割。为了使诊断树生成算法更加简明,可将分割过程作为子程序嵌入到诊断树生成算法。图5为分割子程序的流程图。

图5 分割子程序
2)OPEN表及其指针:在隔离矩阵生成算法中,OPEN表采用5个属性和两个指针,如图6所示。
属性1:模糊组F,它的元素用非负整数0、1、2、3、…表示,且顺序从小到大排列。
属性2:模糊组对应元素个数NF。
属性3:下次分割该模糊组时,采用的测试。
属性4:该模糊组父辈模糊组地址FA。
属性5:该模糊组故障隔离标记。
AD指针:用于OPEN表地址计数,当有新的模糊组产生时,AD指针加1,并在相应的OPEN地址中存入F、NF、 PF、FA和FI,存放顺序按照广度优先原则进行,即新状态放入OPEN表尾部。
BD指针:用于依次从OPEN中取出F、NF、PF、FA 和FI,并判断是否可以进行相关的分割操作。从OPEN表中取出一个状态,则BD指针加1。
当BD=AD时,表示已经将OPEN表1中模糊组已经分割完毕,分割程序结束。
3)其它问题:
(1)当前模糊组个数NF=1时,表明该模糊组分割结束,记录它的隔离向量。
(2)测试已用完,表示分割结束。
(3)当所选测试未对该模糊组进行分割时,将该模糊组存入OPEN表尾部,继续下一次测试分割。
(4)当BD=AD时,程序结束。
4)算法流程图:
图7为OPEN表的算法流程图。

图6 OPEN表及其指针
7 算例
某雷达电子系统共有18个单元,即F1、F2、…、F17、F18,设有6个检测点,即T1、T2、T3、T4、T5、T6。它的相关矩阵如式(17)所示。


图7 算法流程图
根据隔离矩阵生成算法,求得在T1、T2、T3、T4、T5、T6测试顺序下的隔离矩阵如式(18)所示。采用分析法求解该测试顺序下隔离矩阵,与式(18)相同,验证了隔离矩阵的求解算法是有效的。
8 结论
故障隔离矩阵与相关性矩阵既有联系,又有区别。在相关性矩阵的基础上进行故障诊断时,不同测试顺序对应着不同的故障隔离矩阵,不同测试顺序也会产生不同测试费用。测试顺序对测试费用的影响是通过隔离矩阵来计算。测试顺序优化的前提是求解测试顺序对应的隔离矩阵。基于广度优先搜索的隔离矩阵生成算法实现了隔离矩阵自动生成,为测试顺序优化提供了基础。

[1]石君友.测试性设计分析与验证[M].北京:国防工业出版社,2011.
[2]吕晓明,黄考利,连光耀.基于混沌粒子群优化的系统级故障诊断策略优化[J].系统工程与电子技术,2010,32(1):217-220.
[3]石 翌,胡 鹰,李俊杰,等.基于粒子群算法的诊断策略优化技术 [J].计算机测量与控制,2014,22(8):2387-2390,2395.
[4]于劲松,张 帆,万九卿.基于故障相关矩阵的最优测试序列生成方法[J].计算机测量与控制,2009,17(6):1077 1079,1083.
[5]杨 鹏.基于相关性模型的诊断策略优化设计技术[D].长沙:国防科技大学,2008.
[6]王永庆.人工智能原理与方法[M].西安:西安交通大学出版社,2006.
Generating Fault Isolation Matrix Based on Breadth First Search Algorithm
Zhang Yansheng,Qiao Zhongtao,Jing Jianhui
(Department of Missile Engineering,Ordnance Engineering College,Shijiazhuang 050003,China)
Dependency matrix describes the logical relationship between fault and test.isolation matrix describes demand relationship between fault isolation and test in a given test sequence.The effect of test sequence on diagnostic cost can be calculated by isolation matrix.So solving the isolation matrix is a basic condition for optimizing diagnostic cost.There are several problems of isolation matrix,such as easy to confuse with dependency matrix and difficult to solve with traditional analysis method.In this paper,the concept and generation principle of isolation matrix are detailed,and the generation algorithm based on the breadth first search is designed.At last,an example shows that the algorithm is feasible and effective.
test;isolation matrix;breadth first search algorithm
1671-4598(2016)08-0016-05
10.16526/j.cnki.11-4762/tp.2016.08.005
:TP206
:A
2016-02-12;
:2016-02-28。
张延生(1974-),男,河北武安人,博士,主要从事测试性与人工智能方向的研究。

