基于SA－WNN模型的水电机组故障诊断研究

梁红梅1，肖志怀2

（1.新疆昌吉职业技术学院，新疆昌吉 831100；2.武汉大学水力机械过渡过程教育部重点实验室，武汉 430072）

基于SA－WNN模型的水电机组故障诊断研究

梁红梅1，肖志怀2

（1.新疆昌吉职业技术学院，新疆昌吉 831100；2.武汉大学水力机械过渡过程教育部重点实验室，武汉 430072）

针对水电机组振动故障征兆和故障类型的非线性特性及传统小波网络在故障诊断中的缺陷，设计了一种基于模拟退火算法的小波神经网络（SA－WNN）故障诊断模型；将SA－WNN诊断模型应用到水电机组4种典型故障，验证其可行性；实例结果表明，与传统小波网络相比，基于模拟退火算法优化的小波神经网络训练次数少，收敛精度高，为水电机组故障诊断提供了新途径。

模拟退火算法；小波神经网络；水电机组；故障诊断

0 引言

水电站在电网系统中承担着调频、除峰填谷、黑启动等重任，确保了系统稳定运行［1］。水轮发电机组是水电站的核心，庞杂的机组结构及组成部件高度的集成化使得水电机组运行过程中的故障率明显提升，故障类型也更加复杂。据统计，水电机组大约80%的故障表现在机组振动上［2］。水电机组区别于其他旋转机械，其振动信号受到水力因素、机械因素及电气因素的共同影响［3］，且三者呈现出高度的耦合性。耦合效应导致振动信号拥有水、机、电三性特征，非线性化突出。所以故障诊断遇到了一定的技术难题，即无法利用简单的‘故障字典法’建立振动信号特征量与故障原因两者之间一对一的线性关系模型以实现故障诊断。鉴于水电机组振动故障的复杂性、耦合性，故障诊断通常采用建立振动特征集与故障集之间非线性诊断模型的方法来实现两者的有效映射。智能控制技术的普及为故障诊断提供了多种智能方法，如BP网络、贝叶斯网络、SVM等，可有效建立所需的非线性模型，在水电领域取得了不错的诊断效果［4-6］。虽然BP神经网络非线性映射能力很强，但其收敛速度慢、容易陷入寻优函数局部极值的缺陷使得故障诊断训练过程中难以得到最优解；贝叶斯网络节点条件概率模糊式确定形式直接影响故障识别精准度；面对多故障分类问题时，支持向量机模型需建立多个子分类器，故障诊断存在运算速度慢、效率低的缺陷。

自经问世，小波分析便得到的深层次研究。凭借小波基函数自由伸缩和平移特性及其良好的时频分辨能力［7］，小波技术已成为故障诊断领域处理非平稳随机信号的有效分析手段［8］。以小波分析为基础、用小波基函数替代神经网络固有的激励函数构成的紧致型小波神经网络（Wavelet Neural Network，WNN）是一类新型前馈网络［9］。这种网络结构融合了小波分析时频域多尺度局部细化特色和神经网络自学习功能，具有较强的逼近、容错和模式分类能力［10］，为故障诊断领域提供了新途径［7，9］。但WNN没有特定算法训练网络参数，其采用的梯度下降算法易陷入函数极值点的缺陷严重影响网络训练的精度和速度［11］。国内外已有一定科研文献提出利用启发式智能算法对小波网络结构改善、对网络参数寻优。文献11和12分别采用粒子群算法和遗传算法优化WNN，并应用于齿轮箱和电力变压器的故障诊断，提高了诊断精度和速度［11-12］。但粒子群算法与遗传算法存在的早熟收敛现象［13］会使函数过早陷入优先搜索得到的局部极值而忽略其他极值点，从而难以收敛到全局最优点。因此，研究在全局内具有较强寻优能力的算法成为解决多变量、非线性组合优化问题的迫切需求。

模拟退火（Simulated Annealing，SA）算法属于一类随机寻优理论，可以在全局搜寻到函数的最优解。通过待优化变量的随机变化，网络能够朝着目标函数减少及以某种概率分布接受目标函数增大的方向调整，防止网络陷入局部最小，从而逼近全局最优解。Kirkpatrick等成功地将其引入到组合优化问题，并在图像处理、通信、经济等领域得到广泛应用［14］。本文结合SA可以跳出局部极值点和小波网络时频局部化的优点，构建模拟退火－小波网络（SA－WNN）。利用水电机组振动信号的特征频率和故障类型作为模型输入和输出，使用SA算法取代梯度下降法优化WNN的权值等参数，构建基于SA－WNN的故障诊断模型，并用典型故障数据检验其识别效果。诊断结果显示，与基于BP及WNN的诊断模型相比，该方法训练时间更短，故障模式判别更精确，为水电机组振动故障智能在线诊断提供了新方法。

1 模拟退火算法原理

固体的退火机理：高温固体缓慢冷却至低温的过程中，内部微粒状态由紊乱逐渐趋于规则有序排列，相应地固体内能慢慢减为最小。模拟退火算法处理寻优问题时，学习过程类似固体退火，目标函数模拟为固体内能，给定初始温度，随后以一定方式降温，直至搜索到最优的结果。不同于梯度下降，SA算法优点是寻优过程中会以一定概率舍弃目标函数局部极值继续搜索解空间内其他解，防止坠入局部极小“陷阱”，进而确保查寻到解为全局最佳。研究已证实，SA算法是一类全局寻优理论，收敛至全局最优解的概率接近1［15］。

SA算法包含S、C（S）、f，其中f是目标函数，S是当前解，C（S）为解空间。设T为温度，对组合问题进行寻优就是对不同T下S重复“C（S）内新解形成－计算f差值－新解接纳或拒绝”迭代的过程。

首先在C（S）内生成新解S′，紧接着根据式（1）求取S′的接纳率p：

当每个温度T下搜索L次后按照一定规则降温；随后在新的温度下重复上述过程。

2 小波网络

采纳文献［7］构建的紧致型小波网络，其结构和参数分别如图1、表1。

图1 小波神经网络结构

表1 小波网络各项参数

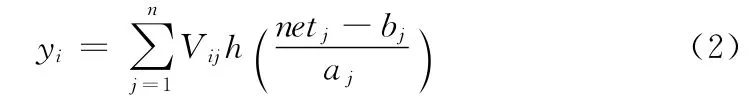
WNN训练与BP相似，需要确定训练对象，即误差函数E，如（3）式：

式中，L为训练样本的数量；di（i＝1，2......n）为目标输出向量。

3 模拟退火-小波网络（SA-WNN）模型

本文将SA算法与WNN融合在一起，构造基于SAWNN的故障诊断模型，结构如图2。模型对参数寻优时不采用梯度下降，更换为SA算法。新算法待优化参数和目标函数分别对应Wjk、Vij、aj、bj及误差函数E。

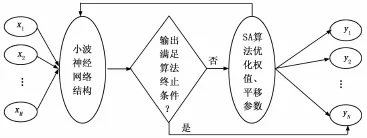
图2 SA－WNN模型结构

3.1 模型优化参数原理

模拟退火算法中的三函数两准则，以及初温决定SA算法的优化性能，本文对6种影响因素设置如下规则：

1）状态产生函数。新状态产生方式如式（4）：

其中：ΔS是符合柯西分布的随机变量，α为控制参数，这样既可在S局部邻域内寻优，也能给S添加相对大幅增量进入S的全局邻域内寻优，以跳出局部极小。

2）状态接受函数。采用式（1）确定S′的接受率，如果ΔE＜0，接受S′；否则以p＞random［0，1］作为S′的接受标准。

3）温度更新函数。采用式（5）降温：

其中：T0为初温，n降温次数，c为制冷率（0＜c＜1）。

4）初温确定。初温T0根据式（6）确定：

式中，Δc、p0分别为初始两状态间的能量差值和接受率，优化对象不同，输入量不同，故初温大小需根据具体情况确定。

5）内循环终止准则。即马科夫链长度L，确定同温下解的搜索次数。

6）外循环终止准则。采用两种结束条件：

（1）降温超过指定次Z；

（2）误差E＜λ，即认为寻优成功，结束算法。若降温次数超过Z且E≥λ，认为优化失败。

3.2 模型优化具体步骤

模型优化流程如图3所示。

图3 SA－WNN算法流程图

1）初始化网络权值Wjk、Vij、尺度因子aj、位移因子bj、初温T0、外循环最大次数Z、马科夫链长度L。对m＝1，…，L做第2）至第6）步。

2）计算平方误差E；判断是否满足收敛条件。若是，输出当前解，结束算法；否，转至下一步。

3）Wjk等参数按照（4）式扰动产生新状态Wjk*＝Wjk＋计算其隐层和输出层的输出及平方误差和E′。

4）计算ΔE＝E′－E。

5）若ΔE＜0，接受Wjk*等参数为新状态，Wjk＝；否则以p＞random［0，1］的方式接受Wjk*等参数。

6）重复2）～5），当m＝L时，转至7）。

7）对T降温，n＝n＋1，重复2）－6），直到达到终止条件，或指定迭代次数Z。

4 典型故障诊断实例

4.1 模型结构参数确定

目前水电领域故障诊断应用最为广泛的方法是通过提取振动信号的频域特征，获得表征故障类型的频率分量幅值，并以此作为诊断模型的特征输入量，实现对故障特征集的函数映射关系。本文采用机组振动频谱幅值域的（0.4～0.5）f（f为机组转频）、1f、2f、3f、＞3f作为输入层特征向量，涡带偏心、不平衡、不对中及正常状态4种故障类型作为诊断对象。网络输出采用单输出结构，并定义1、2、3、4分别代表上述4种故障的输出值，利用模拟退火－小波网络进行水电机组振动故障识别、诊断。

为简化模型训练时输入数据运算，将4种故障的训练样本和测试样本归一化，确保输入的频率幅值在［0，1］内，表2和表3分别为网络训练样本和测试样本［10］。

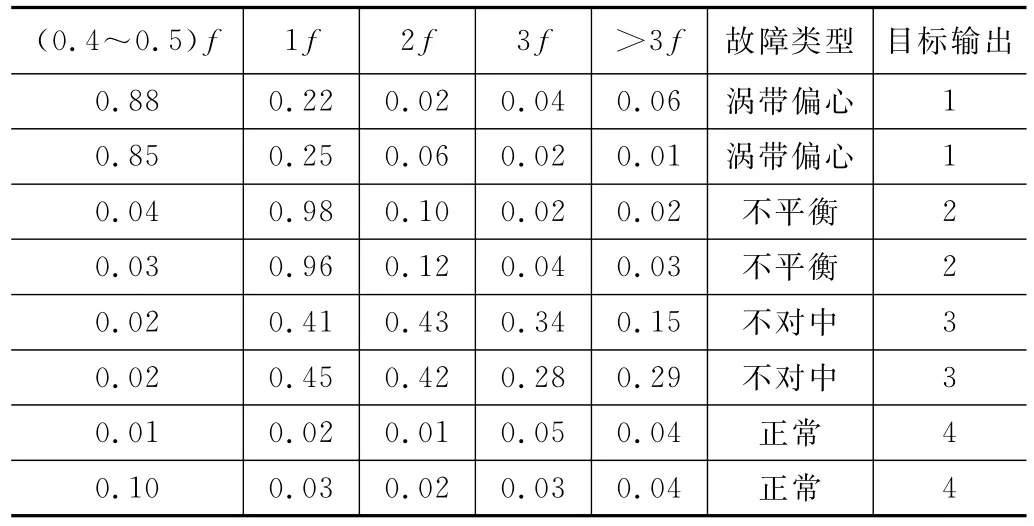
表2 训练样本

表3 测试样本

4.2 训练结果分析

图4是SA－WNN诊断模型误差曲线。当降温至第7次时，误差值便降到0.007，低于期望误差，算法结束，耗时0.799 s。观察全程七次降温误差值E发现，E5＞E4＞E3。误差经历两次短暂连续增长后重新回到下降趋势，再经过两次降温误差便降到0.01以下，达到训练目的。误差值两次增大现象表明寻优过程中以某个概率接受了非优解，改变了模型训练方向，及时跳出局部极值点。从整个寻优过程可以看出，SA算法不像梯度下降算法那样一味追求误差递减方向训练，克服了误入局部极值的不足，进而在全局范围内搜索到了全局最优解，大大降低了搜索时间，提高了寻优效率。

为比较SA－WNN诊断效果，分别利用WNN、附加动量项BP神经网络在同一计算机上对训练学习样本。两者的训练曲线分别如图5、图6，两者误差值在初始训练阶段（WNN 前50步内，BP前100步内）下降的很快，随后速率大幅降低，误差曲线趋于水平。当误差函数值降到期望误差0.01以下时，WNN迭代206步，耗时3.693 s；附加动量项BP网络训练547步，耗时10 s。

图4 SA－WNN网络训练曲线

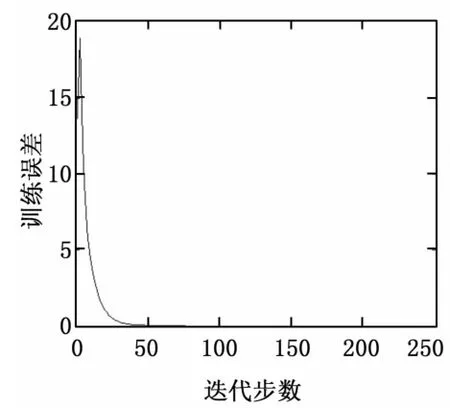
图5 WNN网络训练曲线

图6 附加动量项BP网络训练曲线

利用表3中样本测试经过训练后3种诊断方法的故障识别精度，结果如表4。根据（3）式计算3种诊断网络的误差值，误差及诊断时间对比如表5。

表43 种诊断网络输出值

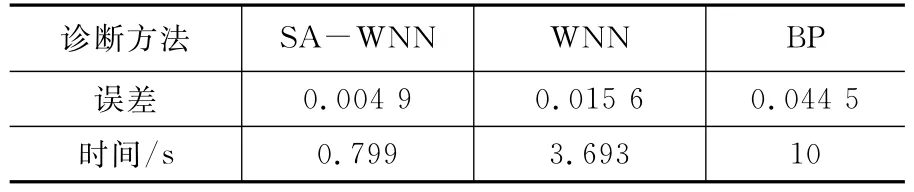
表55 种诊断网络误差及训练时间

分析以上诊断结果，可得出如下结论：

1）表4可以得出，针对同一故障，SA－WNN、WNN、BP3种方法诊断结果与目标值十分接近，都能有效识别故障类型。

2）表5中，WNN和BP训练时间都较长，因为WNN采用的梯度下降算法及BP网络的算法都易陷入局部极值，大大降低了收敛速度；SA－WNN模型结合了SA算法能跳出局部极值的优点及小波分析良好的时频局部化特性，诊断时间最短，且精确识别典型故障，诊断精度最高。

3）较BP、WNN模型，SA－WNN诊断模型较优，能够满足水电机组故障实时诊断的需求。

5 结语

小波神经网络采用的梯度下降算法易陷入局部极小值，大大降低了训练速度，难以满足水电机组故障实时在线诊断的要求。结合模拟退火可以跳出局部极值点和小波网络时频局部化的优点，本文提出了一种基于模拟退火－小波神经网络的诊断模型，使用模拟退火算法替代梯度下降法优化网络参数并利用水电机组典型故障数据验证其可行性和有效性。实例诊断表明，本文所采用的模拟退火算法比BP算法及小波网络算法的故障识别精度高、收敛速度快、诊断效果优，为水电机组故障诊断开辟了新方法。

［1］陆亚轻，涂兴怀，张彦南，等.水电站在电力系统中的作用［J］.能源与环境，2009（5）：16-18.

［2］杨晓萍，解建宝，孙超图.水轮发电机组振动故障诊断的神经网络方法研究 ［J］.水利学报，1998（S1）：95-98.

［3］沈 东，褚福涛，陈 思.水轮发电机组振动故障诊断与识别［J］.水动力学研究与进展，2000，15（1）：129-133.

［4］符向前，刘光临，蒋 劲.BP神经网络在水轮发电机组状态监测与诊断系统中的应用［J］.武汉大学学报（工学版），2002（1）：24-28.

［5］华 斌，周建中，喻 菁.贝叶斯网络在水电机组故障诊断中的应用研究［J］.华北电力大学学报，2004（5）：33-36.

［6］邹 敏，周建中，刘 忠.基于支持向量机的水电机组故障诊断［J］.中国农村水利水电，2008（1）：114-116，119.

［7］彭文季，罗兴锜.基于小波神经网络的水电机组振动故障诊断研究［J］.水力发电学报，2007（1）：123-128.

［8］梁武科，罗兴锜，张彦宁，等.水力发电机组振动故障诊断系统中的信号预处理［J］.水力发电学报，2003（3）：114-120.

［9］罗跃纲，陈长征，曾海泉，等.基于信息融合的集成小波神经网络故障诊断［J］.东北大学学报（自然科学版），2002，23（8）：802-805.

［10］卢 娜，肖志怀，符向前.基于蚁群初始化小波网络的水电机组振动故障诊断［J］.水力发电学报，2014（2）：251-258.

［11］毛鸿伟，潘宏侠，刘文礼，等.基于粒子群优化的小波神经网络及其在齿轮箱故障诊断中的应用［J］.振动与冲击，2007，26 （5）：133-136.

［12］潘 翀，陈伟根，云玉新，等.基于遗传算法进化小波神经网络的电力变压器故障诊断［J］.电力系统自动化，2007，31（13）：88-92.

［13］雷浩辖，刘 念，崔东君，等.基于GA与PSO混合优化FCM聚类的变压器故障诊断［J］.电力系统保护与控制，2011，39 （22）：52-56.

［14］曾利平，王海波，何岳华，等.一种模拟退火小波网络的电力变压器故障诊断［J］.计算机仿真，2011（7）：316-321.

［15］尤丽华，吴静静，王 瑶，等.基于模拟退火优化BP神经网络的p H值预测［J］.传感技术学报，2014（12）：1643-1648.

Study for Vibration Fault Diagnosis of Hydro－turbine Generating Unit Based on SA－WNN

Liang Hongmei1，Xiao Zhihuai2

（1.Xinjiang Changji Vocational and Technical College，Changji 831100，China；2.Ministerial Key Laboratory for Hydrodynamic Transients，Wuhan University，Wuhan 430072，China）

Aiming at fault diagnosis for the vibration fault symptoms and fault types the fault diagnosis model based on simulated annealing algorithm of the wavelet neural network（SA－WNN）is proposed.The SA－WNN diagnostic model is applied to four kinds of typical faults of hydro power plant to verify its feasibility.The results show that，compared with the traditional wavelet network and BP，the number of wavelet neural network training based on simulated annealing algorithm is less，and the convergence precision is high，which provides a new way for the fault diagnosis of hydroelectric generating units.

simulated annealing algorithm；wavelet neural network；hydro－turbine generating unit；fault diagnosis

1671-4598（2016）08-0024-04

10.16526／j.cnki.11－4762／tp.2016.08.007

：TM312

：A

2016-02-23；

：2016-03-08。

国家自然科学基金项目（51379160）。

梁红梅（1968-），女，副教授，主要从事水电机组自动控制方向的研究。