大规模光伏发电并网概率潮流计算及对电网的影响

金 楚， 黎嘉明， 徐沈智， 文劲宇

(强电磁工程与新技术国家重点实验室(华中科技大学电气与电子工程学院)，湖北 武汉 430074)

·专论与综述·

大规模光伏发电并网概率潮流计算及对电网的影响

金 楚， 黎嘉明， 徐沈智， 文劲宇

(强电磁工程与新技术国家重点实验室(华中科技大学电气与电子工程学院)，湖北 武汉 430074)

随着并网光伏发电容量的规模越来越大，光伏发电固有的波动性和不可控性导致其大规模并网时会使潮流分布发生变化甚至潮流反向，对电网的安全稳定运行造成影响。建立了光伏发电系统的潮流计算模型，以IEEE 14节点系统和西北某省级电网系统为研究算例，对含光伏的电力系统进行概率潮流计算，全面分析了不同光伏接入容量、不同光伏接入点及不同光伏出力相关性的情况下大规模光伏并网对系统潮流的影响。结果表明光伏接入容量越大，电压及支路潮流的波动和越限概率也越大，光伏接入点将影响系统网损及光伏极限接入容量，并发现光伏接入对系统潮流的影响具有方向性，且光伏电站出力相关性不可忽略。所得结论可为电力系统新能源规划与运行提供决策参考。

光伏并网；概率潮流；相关性

近年来，光伏发电发展迅猛，光伏装机容量在电网中所占的比例越来越大。预计到2020年底中国光伏发电总装机容量将达到150 GW[1]。与风电类似，光伏发电固有的波动性和不可控性导致其大规模并网时会使系统潮流分布发生改变甚至潮流反向，同时带来电压波动或者电压越限等问题，这将对电网的安全可靠运行造成影响。目前，关于风电并网对电力系统影响的研究已较为成熟，但是有关光伏并网对电网影响的研究仍比较欠缺。已有的文献大多是关于分布式光伏接入对配电网的影响[2-6]，而针对大规模集中式光伏并网对系统的影响，目前研究并不多。随着各国百兆瓦级甚至千兆瓦级光伏电站的建设，光伏发电集中式并网成为研究的热点问题和发展的主要方向[7]。因此，研究大规模光伏集中式并网对电力系统的影响非常必要。

光伏并网主要对电网潮流分布、电能质量、动态特性等方面产生影响。文献[2-4]运用确定性潮流方法(determined load flow, DLF)研究了分布式电源并网相关潮流问题，提出分布式电源接入的处理方法。但是，光伏发电的出力由实时光照强度决定，存在明显的随机性，运用确定性潮流计算方法不能全面地反映和评价其影响因素及程度，而采用概率潮流计算(probabilistic load flow, PLF)可以反映电力系统中各种不确定性因素对系统运行的影响。

概率潮流计算方法包括蒙特卡洛模拟法[8-10]、半不变量与Gram-Charlier级数展开[6,11]及点估计法[12-13]等。其中，文献[9]提出含光伏的系统电压评价指标，但仅考虑了单光伏电站的影响；文献[10]在满足电压约束的条件下计算了辐射状配电网能接纳的分布式光伏容量，其中光伏均位于电网末端；文献[11]研究了分布式光伏对配电网的影响，得出光伏并网有利于提高电压质量的结论，而这对于集中式光伏并网并不一定成立；文献[12]分析了光伏并网后电压概率密度分布(probabilistic density function, PDF)，但忽略了随机变量间的相关性。在考虑了相关性的文献中，文献[14]计及了风速区间和光照强度区间的相互约束，文献[15]研究了光伏机组开停机时间的联合概率分布，文献[16]考虑了节点、支路间的相关性，研究了电压分布的特点，但以上都未考虑光伏并网对系统支路功率的影响。

本文建立了光伏发电系统的稳态模型，从光伏接入容量，光伏接入点等角度，考虑光伏电站出力相关性，基于IEEE 14节点系统及西北某省级电网2个算例，定量研究了大规模集中式光伏并网对系统节点电压及支路潮流的影响。

1 光伏发电系统潮流计算建模

1.1 光伏发电系统潮流计算模型的构成

光伏发电单元主要包括光伏电池阵列、控制模块、逆变器等几个部分。在潮流影响分析中，光伏发电单元的建模不需要考虑其控制系统调节过程的动态特性，只需关心其稳态输出结果，即在给定的光照、环境温度输入序列的情况下根据光伏电池特性以及变流器配置给出相应的电功率输出序列，其稳态模型主要有以下3个特点：

(1) 逆变器在光伏稳态模型中表现为交直流侧的功率平衡方程；

(2) 由于最大功率点跟踪(maximum power point tracking，MPPT)控制[17]的实施，稳态模型的有功输出近似等于当前光照强度、电池温度下的最大光伏功率(考虑限功率控制除外)；

(3) 各闭环控制调节过程在稳态建模中不予考虑。

因此光伏发电的稳态模型包括如图1所示虚线框中的两部分内容，其中光伏发电系统实际注入电网的有功功率始终保持在最大功率点，由其MPPT控制所保证，用于潮流计算的光伏发电系统模型如式(1)所示。本文潮流计算中光伏并网节点作为PQ节点处理，光伏电站的无功输出设置为0。

(1)

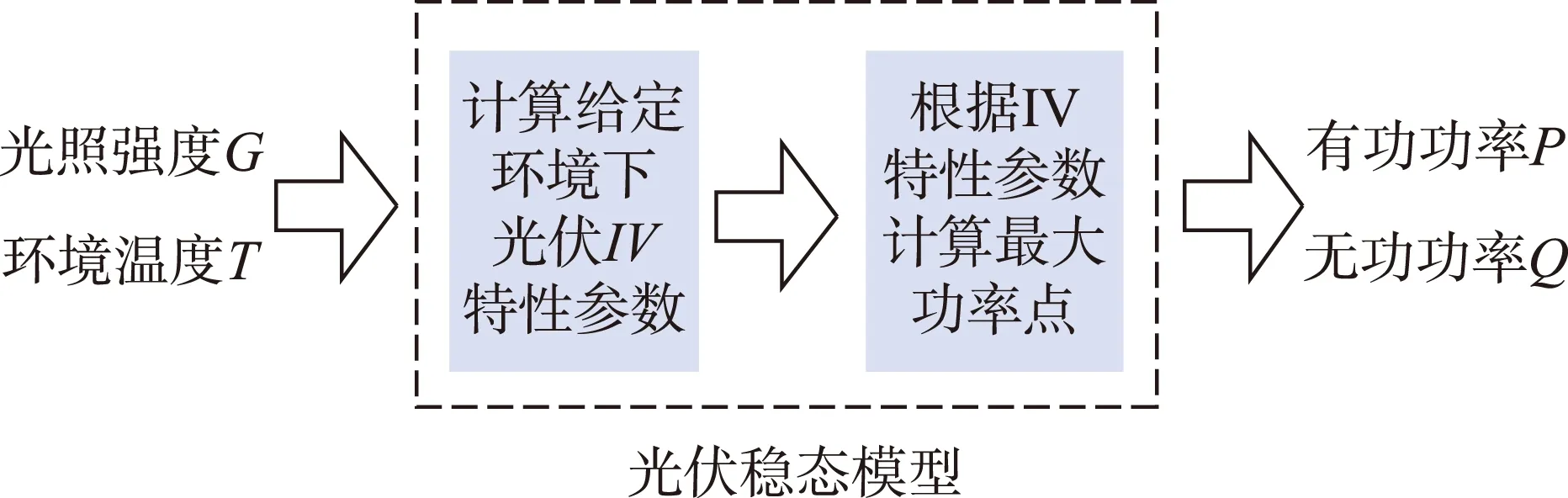
图1 光伏电站稳态模型功能示意图

1.2 基于MPPT控制的光伏发电系统潮流计算模型

实际中单一光伏电池的输出电压较低、输出功率较小，为匹配大容量变流器的输入电压要求，一般需要将大量的光伏电池串联构成光伏模块以提高其输出电压，再将大量光伏模块并联构成光伏电池阵列以增加逆变器的容量利用率，如图2所示。出于统一MPPT控制和缓解热斑效应的需要，工程上组成同一光伏阵列的光伏电池在特性上要求尽可能地相似，因此在建模中可以忽略其差别，根据串联数量NS、并联数量NP可由式(2)建立起光伏阵列与光伏电池输出量之间的关系，式中ICELL和VCELL分别为光伏电池的输出电流和电压，I和V分布为光伏阵列的输出电流和电压。

(2)

基于上述结构，本文采用的光伏电池的稳态建模等效电路如图3所示，其特性函数为单指数等效模型[18,19]如式(3)。

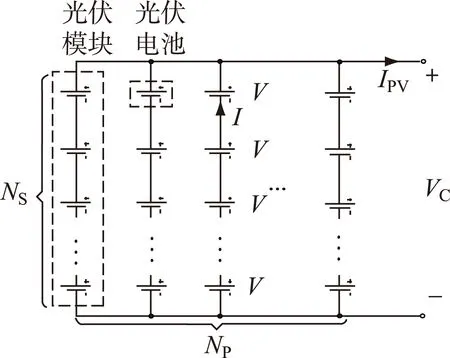
图2 光伏电池阵列结构示意图

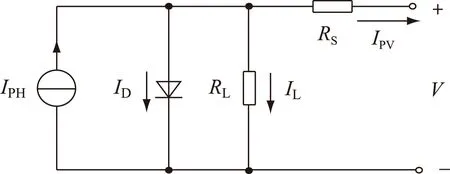
图3 光伏电池的单指数等效模型

图中：IPH为半导体PN结的光生电流；ID为PN结正向导通电流；RL及RS分别表征PN结两侧电极间的漏电阻及接触电阻；IL为极间漏电流。

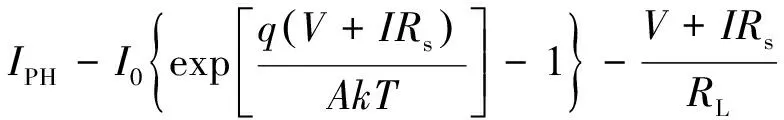
(3)

式中:I0为二极管反向饱和电流;q为元电荷电量;k为玻尔兹曼常数;A为二极管常数;T为环境温度。

工程应用中式(3)的部分物理量不易获得，更常见的参数是厂家提供的在额定光强GSTC和温度TSTC条件下短路电流ISC0、开路电压VOC0、最大功率电压Vm0和最大功率电流Im0等4个特征量(标准条件定义温度为25 ℃，光强为1000 W/m2)，偏离额定工况的任意光强G和温度T条件下，这些特征量的变化可按式(4)进行推算，其中a,b,c为补偿系数，e为自然对数的底数。本文建模时近似认为IPH=ISC、Rs≈0、RL≈∞，从而光伏电池外特性简化为式(5)，其参数m，n与各特征量间的关系如式(6)所示。

(4)

(5)

(6)

将式(2)代入式(5)，得到光伏阵列的I-V关系，进而可以求得光伏阵列的P-V特性如式(7)所示，该式为单峰值函数。按照式(1)，光伏发电的输出为P-V关系的最大值，故对式(7)进行求导并令导函数为0，其唯一零点即为光伏最大功率点，如式(8)所示。由此，可建立起由式(7)和式(9)组成的光伏发电系统潮流计算模型。

(7)

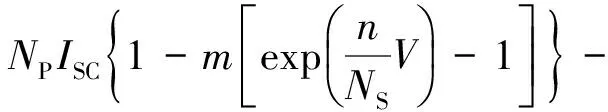
(8)

实际并网光伏电站由大量的光伏发电单元并联组成，现有的研究均是通过单一光伏发电单元输出量的倍增予以模拟。

2 含光伏发电的概率潮流计算及对电网的影响分析

2.1 含光伏的概率潮流计算概述

电力系统潮流计算实质上是求解如式(10)的2个非线性方程组，其中Y为节点注入功率，X为电网状态量，一般包括节点电压幅值和相角，Z为潮流计算结果的输出变量，通常在支路潮流、网损、节点电压幅值间选取。

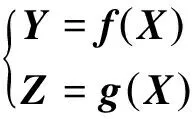
(9)

概率潮流计算主要考虑注入功率向量Y中的部分变量存在随机性，其目的是以随机变量的统计特征求解出系统状态变量X以及输出变量Z的概率分布。

在考虑光伏概率模型时，文献[6]及文献[12]分别认为光照强度服从Beta分布及正态分布。大量实测数据表明，Beta分布能更好地描述光照强度分布特性，则光照强度G的概率密度函数可由式(11)描述(其中Gmax为光照峰值，α,β为Beta分布拟合参数)：

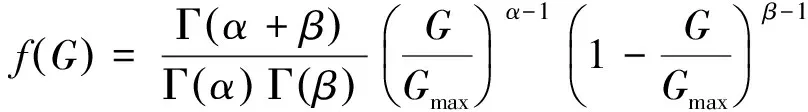
(10)

本文在研究分析并网光伏电站对系统的潮流影响时，认为光伏发电输出有功功率随光照强度随机变化，输出无功功率恒定为0。考虑到计算结果的精确性，采用非贯序蒙特卡洛的方法进行概率潮流计算。含光伏的概率潮流计算过程如图4所示。

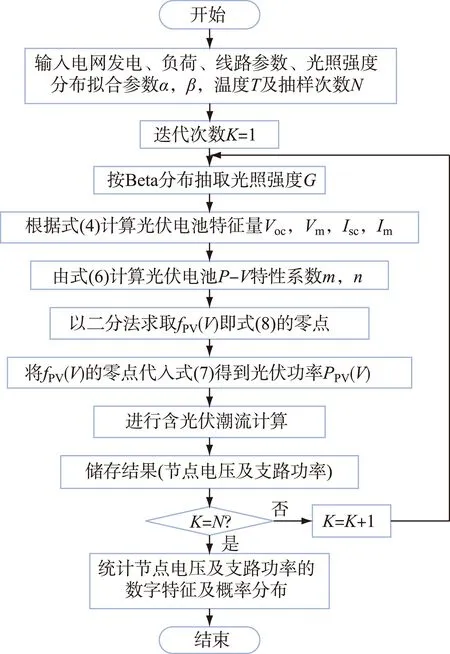
图4 含光伏的概率潮流计算过程

2.2 考虑光伏电站出力相关性的概率潮流计算

由于光伏出力主要受光照强度影响，而光照强度变化规律的基础是日地运动，因此在考虑多光伏电站接入电网的潮流计算时，地理位置相近的光伏电站出力往往具有较强的相关性。本文在计算概率潮流时仍采用蒙特卡洛抽样方法，为考虑相关性以拉丁超立方-Cholesky分解(LHS-CD)技术生成样本[20-22]。

以考虑3个光伏电站接入为例，给定两两间出力的Spearman秩相关系数为ρ12,ρ23,ρ13，可形成相关系数矩阵如式(11)。

(11)

指定待生成的样本数量，用结合Cholesky分解的拉丁超立方采样方法抽取样本，其原理为：利用拉丁超立方方法中的抽样环节分别生成一组反映各自边缘分布的光伏电站出力序列，在拉丁超立方方法中的排序环节中引入相关系数信息进行迭代，仅通过不断调整各序列数据的次序使其符合指定的互相关性[20]。从而能够确保生成的样本既符合不同电站光伏功率各自的边缘分布，也满足电站间出力相关性，其中调整随机出力序列顺序的算法流程如图5所示。

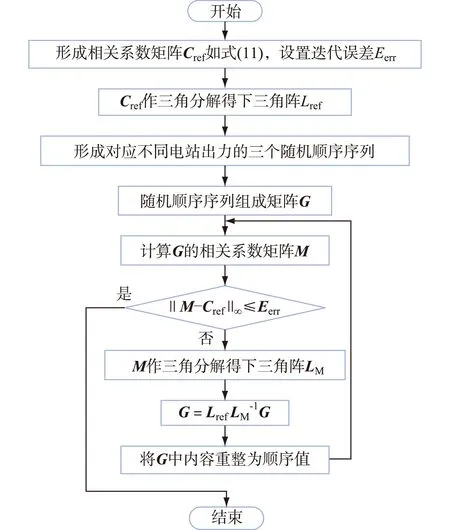
图5 序列顺序调整算法流程

流程中的顺序值指实际数值在序列中的排序位置值(升降序均可)，Spearman秩相关系数仅与顺序值序列有关，与实际值的大小无关。

2.3 大规模光伏并网对电网潮流影响分析

大规模光伏并网对电网潮流的影响主要包括对节点电压及支路功率的影响，选择以下3个影响因素进行考虑，可以较全面地分析大规模光伏并网对系统潮流的影响。

(1) 光伏接入容量。计算统计不同光伏接入容量下电压及功率的概率密度分布，另外，为进一步分析对比光伏并网对各支路潮流的影响程度，选择概率潮流计算得到的支路功率与无光伏并网时原始支路功率的比值的标准差作为衡量对各支路有功功率分散程度的指标，在不同的光伏接入条件下进行比较，再统计越限概率，以灵敏度分析的方式进一步解释。

(2) 光伏接入点。计算不同光伏接入点下系统网损的期望值，分析光伏接入点改变时系统潮流分布的特点，给出选择光伏上网位置的参考依据。

(3) 光伏出力相关性。根据光伏电站出力的相关程度定义光伏出力相关性分为高度相关、中度相关和低度相关3个等级。计算不同相关系数下电压及功率的概率密度分布，分析其波动范围，得到光伏出力相关性对于电网潮流的影响方式。

3 算例分析

本文基于IEEE 14节点系统和西北某省级电网系统，在Matlab平台下，进行含光伏的概率潮流计算，根据3.3节中所述思路和方法，研究大规模光伏并网对系统潮流的影响。

3.1 算例1——IEEE 14节点系统

现以图6所示IEEE 14节点系统为例，分析光伏并网对系统节点电压、支路潮流的影响，本例采用的蒙特卡洛模拟方法采样规模为5000次。系统共五台发电机分别接在节点1、2、3、6、8，其中节点1机组作为平衡机，系统总负荷Pload=259 MW。算例中采用的光伏电池特征参数如表1所示。

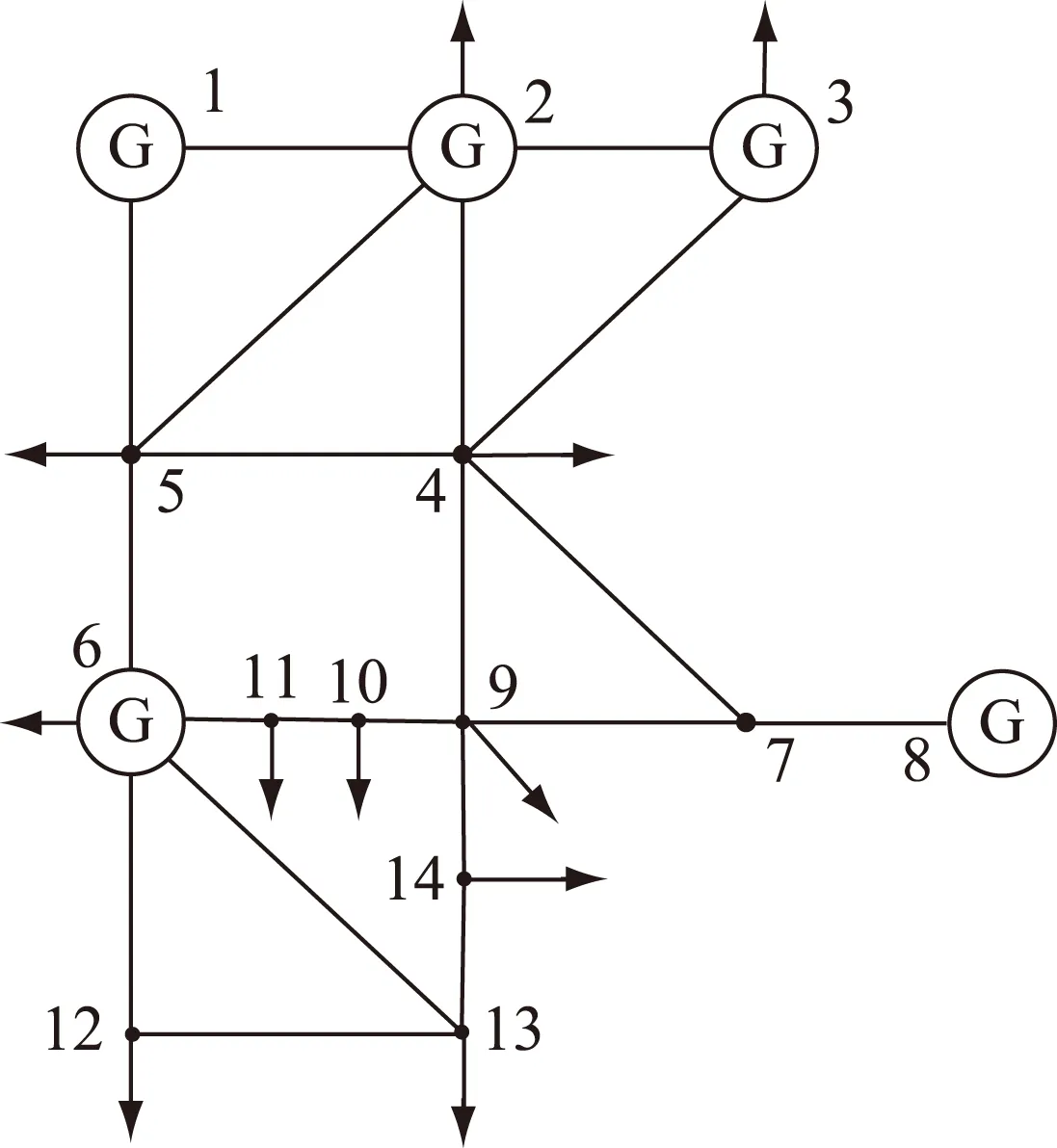
图6 IEEE 14节点系统

项目数值短路电流ISC0/A4．9开路电压VOC0/V43．2最大功率点电流Im0/A4．51最大功率点电压Vm0/V34．4电流-温度补偿系数a/℃-10．0025电压-光照补偿系数b/[(W·m-2)]-10．0005电压-温度补偿系数c/℃-10．00288

以德国3个区域的光照强度特性为例进行含光伏的概率潮流计算，各区域光照强度Beta分布拟合参数如表2所示。

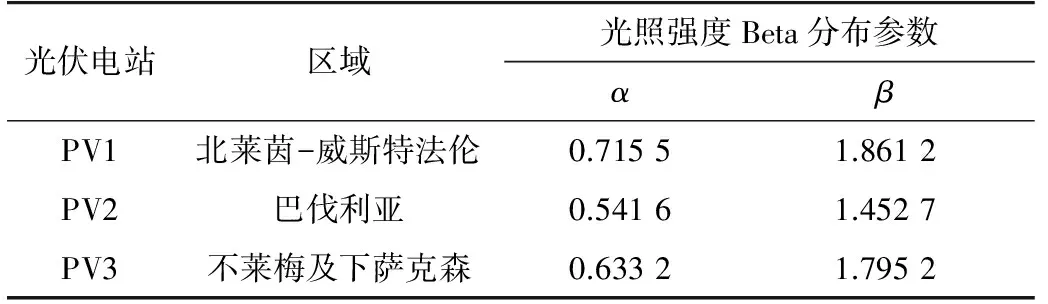
表2 光伏电站光照强度分布参数

3.1.1 光伏并网对节点电压的影响

假定光伏电站PV1接入系统节点4，以节点5为例计算得到光伏接入容量分别为90 MW，100 MW，110 MW，120 MW时电压幅值的概率密度分布函数如图7所示。

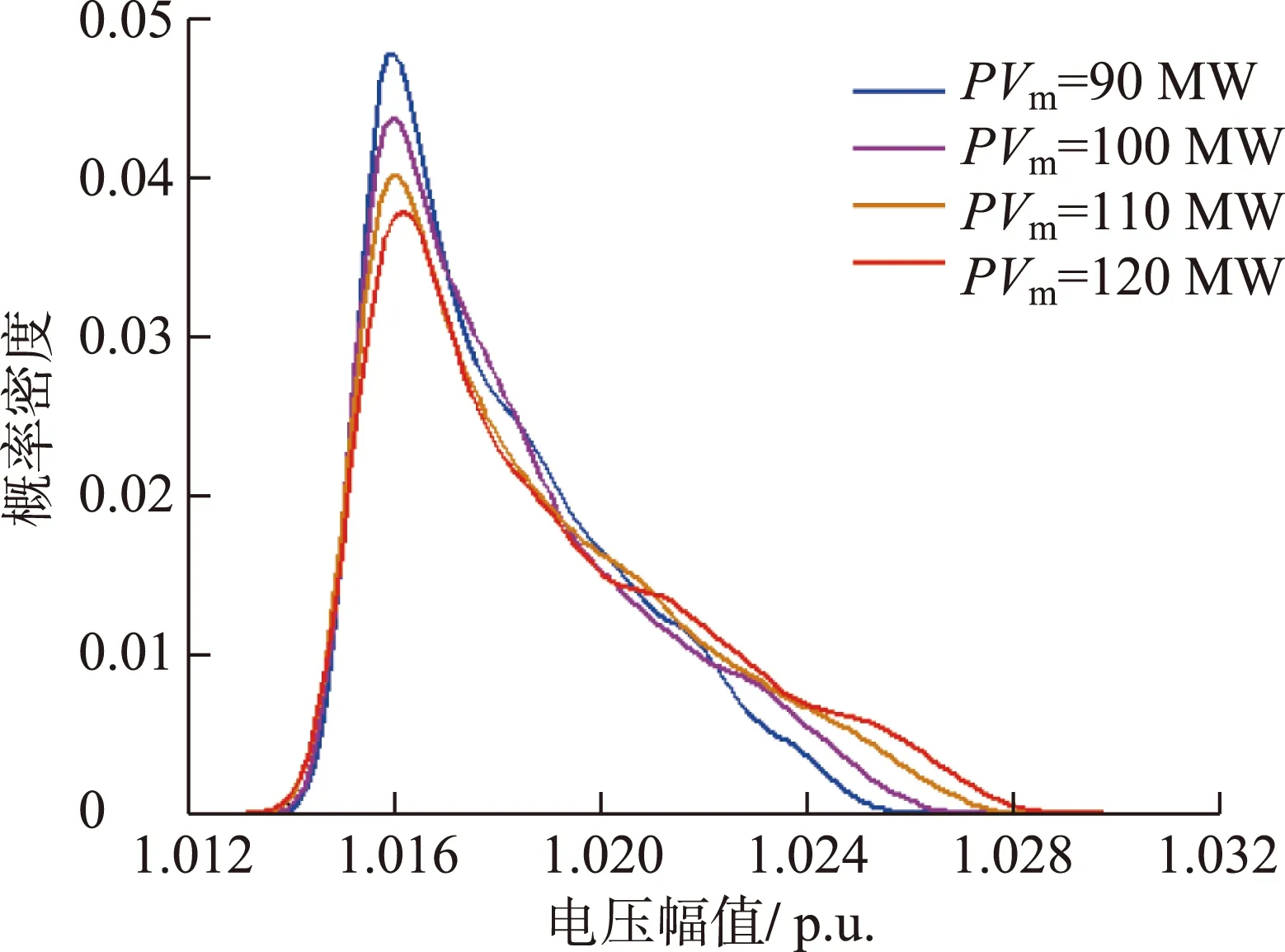
图7 节点5电压概率密度函数(PDF)

固定光伏接入容量为120 MW , 节点4、节点9、节点14、节点13的电压幅值概率密度分布函数如图8所示。

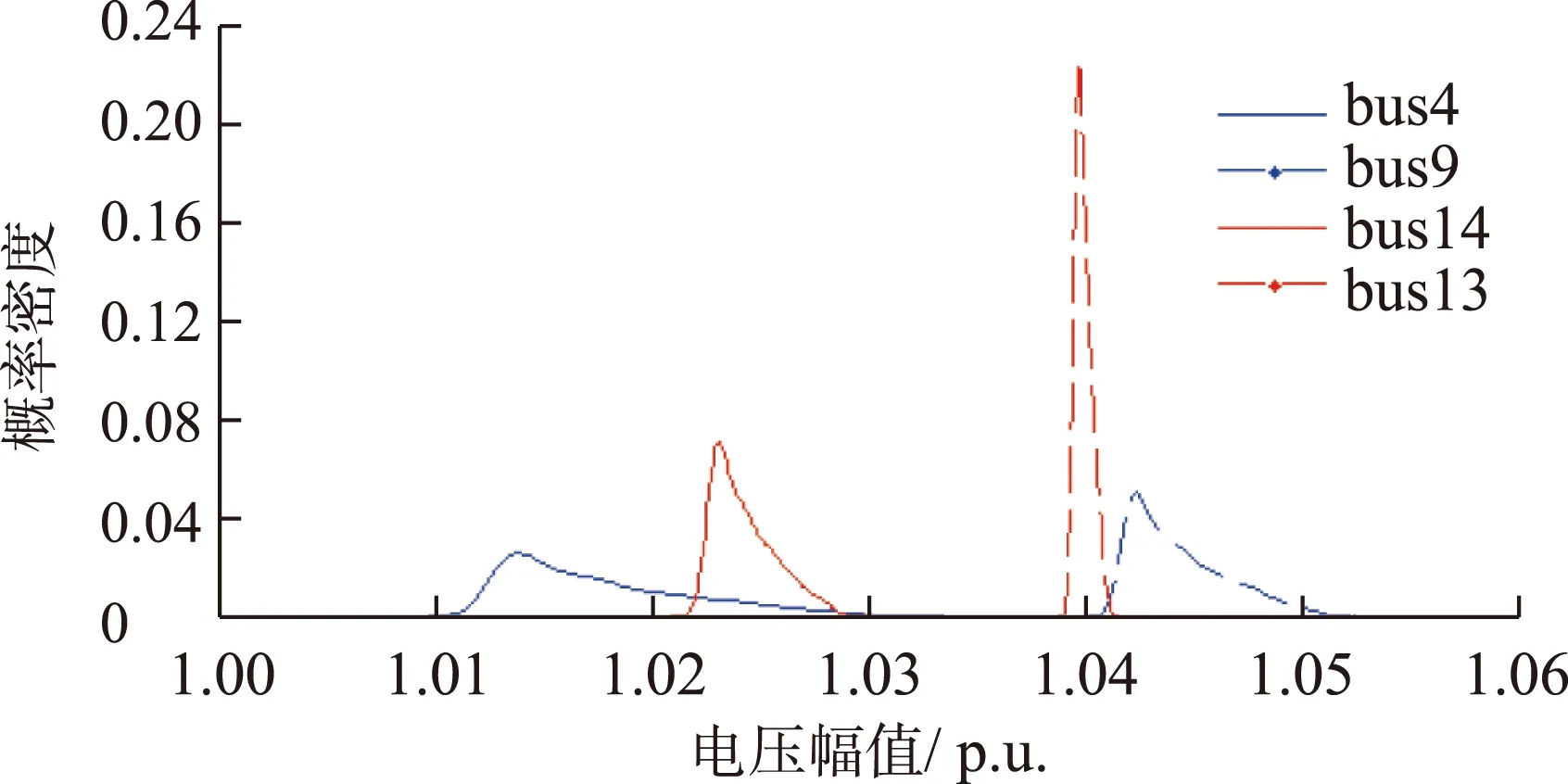
图8 节点电压概率密度函数(PDF)

从图7可以看出，光伏接入容量越大，节点电压概率分布越分散，电压波动性越大。电压波动过大可能造成节点电压越限，对电网的安全稳定运行造成不利影响。节点4、9、14、13距光伏接入点距离逐渐增大，结合图6及图8可知，距离光伏接入点越近，电压幅值波动范围越大。

3.1.2 光伏并网对支路潮流的影响

对于支路潮流，同样可以得到光伏接入容量越大，支路潮流分布越分散，波动性越大的结论。现进一步计算光伏接入容量在80～150 MW范围内变化并以10 MW为步长的情况下支路有功功率的标准差。发现各支路功率相对值的标准差与并网光伏容量近似呈线性关系，且光伏并网容量的增加不改变各线路受影响程度排序。支路功率波动范围最大的是支路4-5、支路2-4、支路3-4，波动范围最小的是支路7-8、支路6-12、支路6-13。

根据概率潮流计算结果统计所有支路潮流越限情况，部分结果如表3所示(超过无光伏支路潮流绝对值的15%则认为越限)。由结果可见支路3-4、支路9-10呈现出极高的越限概率，支路9-14在光伏并网容量超过100 MW时存在越限可能，但概率较低，其余支路不存在越限的情况。

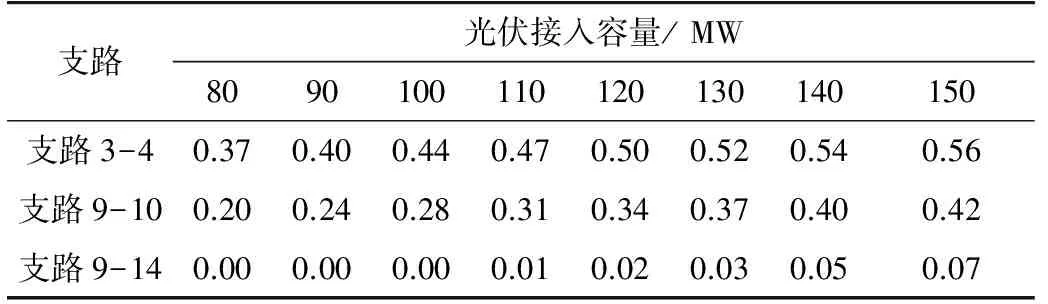
表3 光伏接入容量对支路潮流越限概率的影响

光伏并网后波动范围较大的线路并不一定容易发生越限。其原因是光伏并网后造成的支路功率波动通常是有明显方向性的，仅在功率波动方向恰好与无光伏下支路传输功率方向相同时，光伏并网会对该线路安全运行产生威胁，反之如线路4-5，其波动范围虽大，却不会造成线路过载。

基于以上结论以潮流灵敏度分析进行定性解释。在0～200 MW范围内以10 MW为步长调整节点4注入功率，计算灵敏度系数与原支路潮流的比值如表4所示。其中支路3-4、支路9-10、支路9-14的结果为正且绝对值较大，说明改变单位注入功率时引起的潮流变化最大，因而在统计传输功率越限概率时此3条支路存在最大的风险，与前文结论完全一致。

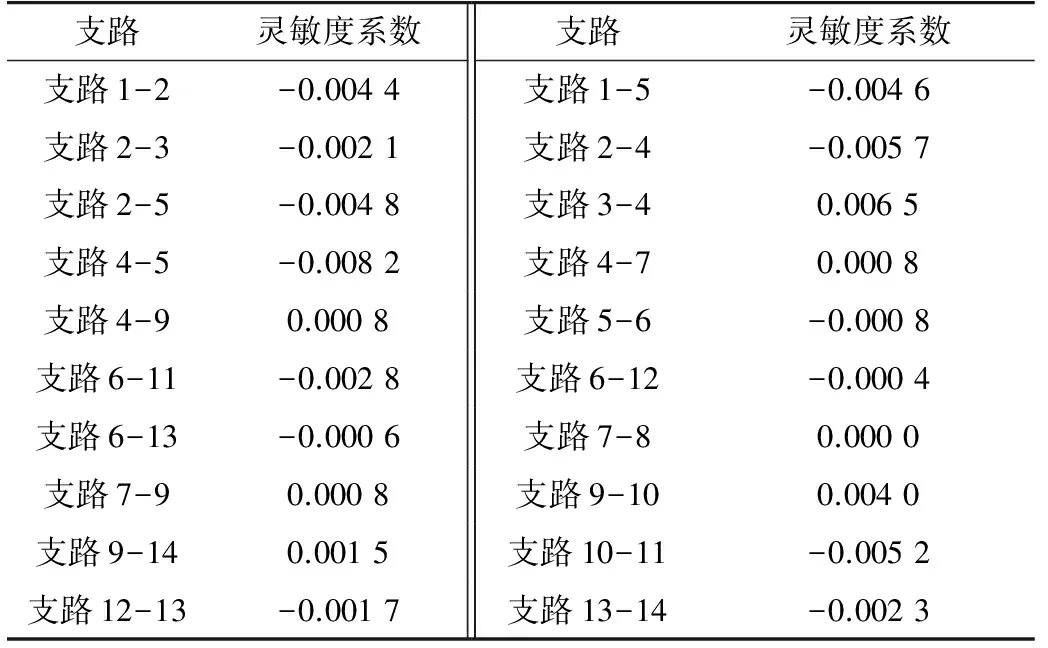
表4 各支路潮流-节点4注入功率灵敏度(相对值)

现取光伏电站接入容量为120 MW不变，由蒙特卡洛抽样计算得到不同接入点情况下系统总网损的期望，如图9所示。

图9 不同光伏接入点下系统的网损期望值

由图9结果可以分析得到结论如下：

(1) 原系统功率主要由节点1和节点2集中送出，光伏并入除节点1、2以外的任意位置均明显有利于均衡有功潮流分布、减小系统网损，并在选择重负荷节点3时获得最小的网损期望值。即从改善网损的角度说，光伏并网点宜选择在系统的功率受端。

(2) 若光伏并网点的送出线均为高电阻标么值的低压线路，例如节点12，并且光伏出力无法在本地消纳，则系统网损改善效果较差。

3.2 算例2——实际省级电网系统

该实际省级电网系统位于西北地区，日照丰富，适合建立集中式规模化的并网光伏发电系统，直接接入输电网。仿真分析表明，单光伏电站并网对系统节点电压、支路潮流的影响与算例1结论一致，限于篇幅，这里不再讨论。该地区电源装机容量约34 893 MW，根据规划该地区电网光伏装机总容量将达到1500 MW，基于目前电网的网架结构，单光伏电站并网很难达到计划的规模。因此考虑采用多个光伏电站接入系统，尽可能地提高并网的光伏装机容量。

3.2.1 光伏出力相关性对电网潮流的影响

由于网架结构、线路参数、无功补偿情况、发电及负荷不同，不同光伏并网点下系统最大光伏接入容量有较大差异。综合考虑光伏上网位置及出力比例分配，选定4个节点进行光伏并网，使总装机容量能够达到规划要求，如所示表5，采用该地区光伏电站实测数据进行概率潮流计算。本例采用基于拉丁超立方采样的蒙特卡洛概率潮流计算方法，采样规模为1000次。

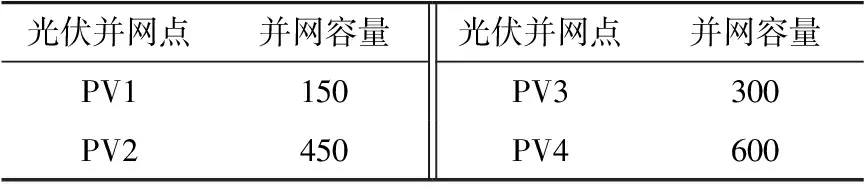
表5 光伏接入点及并网容量 MW

设置3种相关系数(高度相关、中度相关、低度相关)如表6所示。不同相关系数下支路潮流相对值概率密度分布计算结果如图10所示(以无光伏时的原始潮流为基准值)。

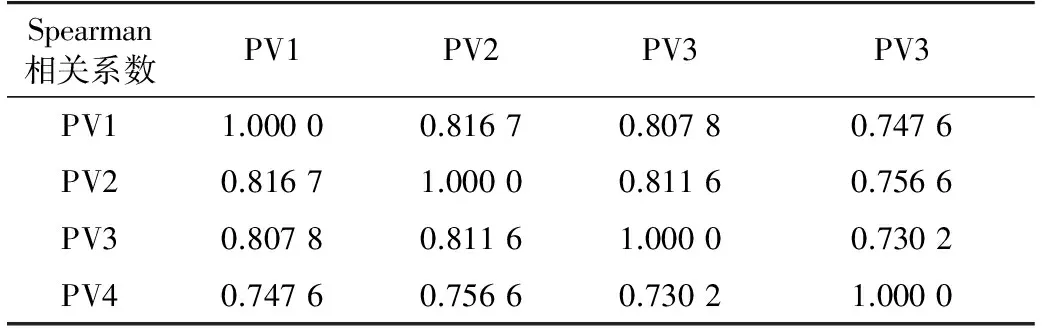
表6 光伏电站出力相关系数设置(a) 高度相关

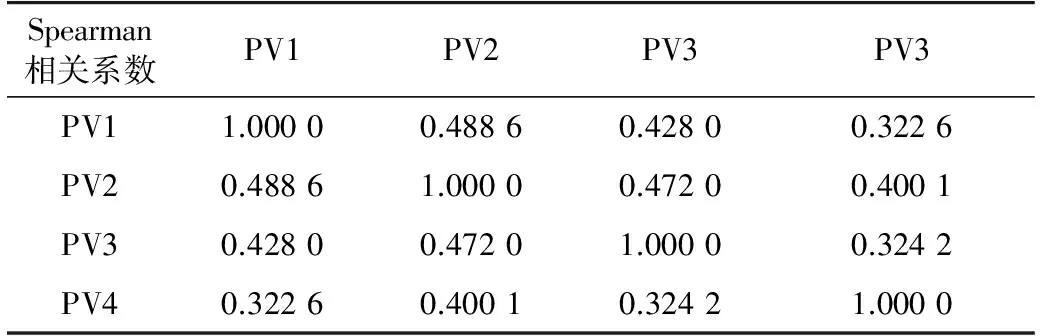
(b) 中度相关

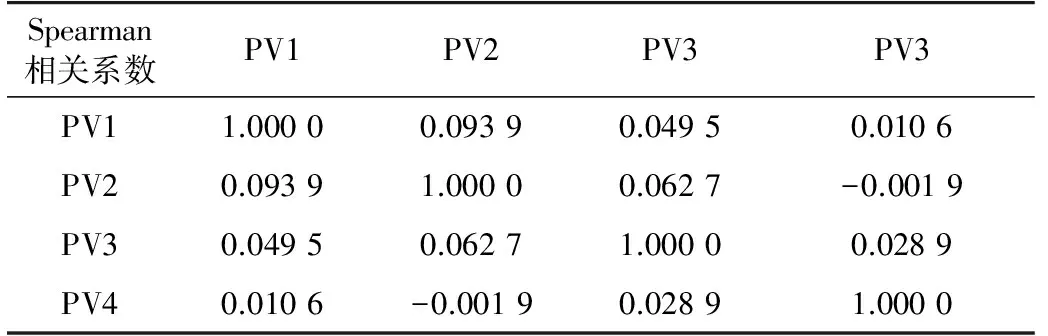
(c) 低度相关

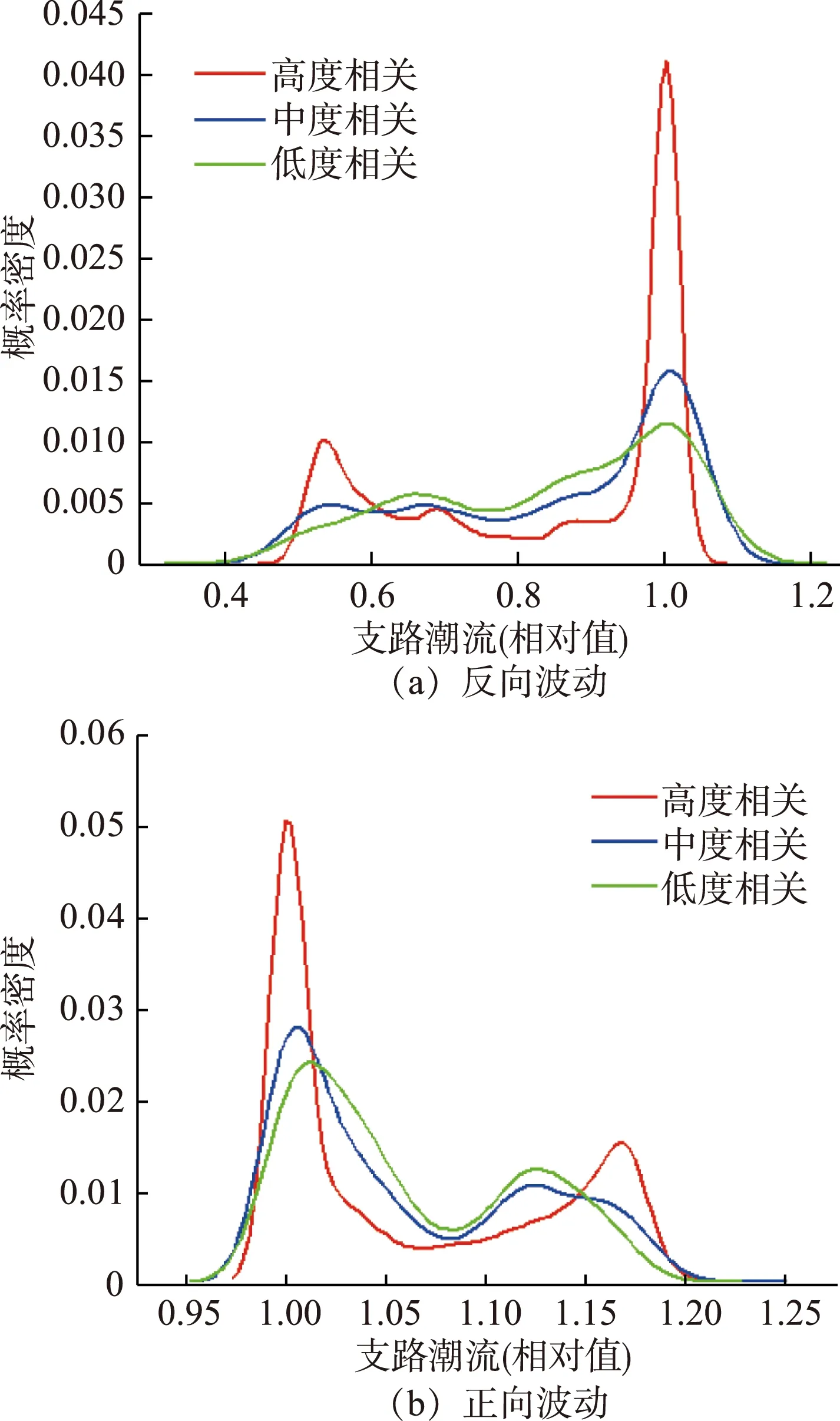
图10 不同相关系数对系统支路潮流的影响

由图10可知，光伏电站出力相关系数越大，支路潮流分布相对越集中，其波动范围相对越小。由于光伏并网引起的支路潮流波动具有方向性，所以并网后潮流可能正向波动或反向波动。如果引起的波动与无光伏时的潮流方向相反，潮流减小，则不会对电网安全运行造成影响，如图10(a)；若引起的波动与原始潮流方向相同，如图10(b)，则有可能造成潮流越限。而在较高的相关系数下，概率密度分布呈现尖峰厚尾的特性，尾部概率较大，由图10(b)可知，此时虽然波动范围较小，但潮流越限的概率反而可能更大(仍以超过原始潮流15%作为判断依据)。因此，在研究光伏并网对系统潮流的影响时，多电站出力相关性不可忽略。对于节点电压，也有类似的结论，这里不再赘述。

3.2.2 制约光伏并网容量的潮流因素分析

在含光伏的电力系统潮流计算中，随着光伏并网容量的增大，可能出现潮流计算不收敛的现象。本文通过Matlab接口程序调用PSASP 6.282进行计算，选择某110 kV母线作为光伏接入点，逐步增加光伏并网容量，获得潮流计算恰好不收敛时的光伏临界装机容量，将其定义为光伏并网容量极限。

将无光伏接入和达到光伏并网容量极限时各节点电压进行比较，各节点电压变化如图11所示，并考察此时电压跌落最明显的节点，得到表7。

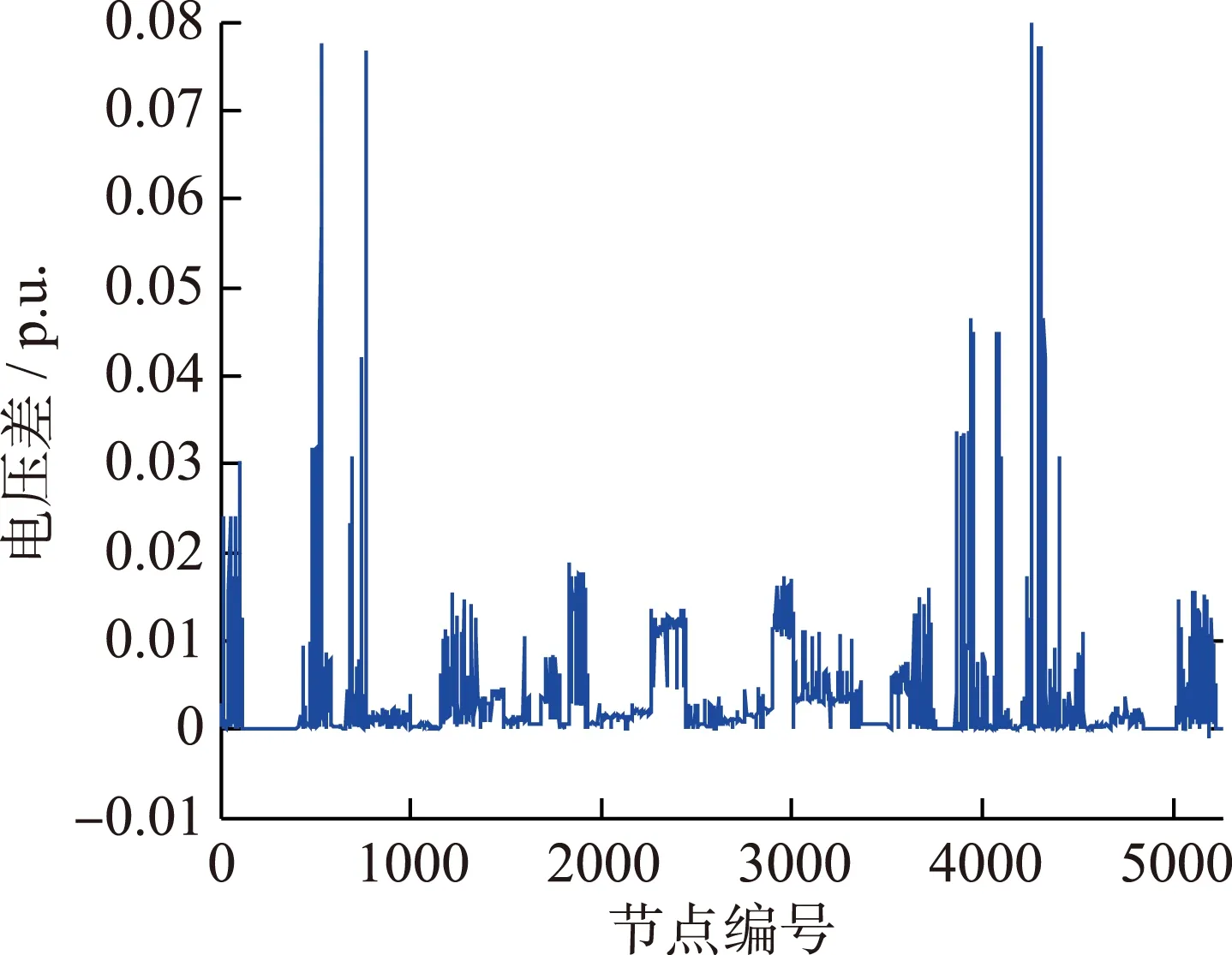
图11 各节点电压差

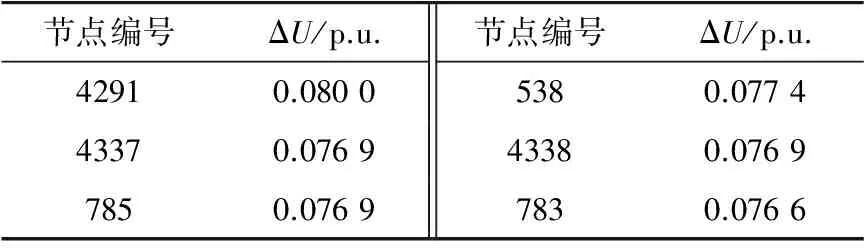
节点编号ΔU/p．u．节点编号ΔU/p．u．42910．08005380．077443370．076943380．07697850．07697830．0766

光伏并网后电网绝大部分节点电压下降，其中电压跌落最明显的点为并网点附近的110 kV母线或其变压器低压侧母线。达到并网极限的主要原因是当光伏并网容量过大后，系统无功补偿不足，并网点附近电压不足以支撑，导致越限，潮流不收敛。

此外，光伏并网点母线类型也是影响系统光伏并网容量极限的因素。改变光伏接入点母线的类型，计算得到光伏接入极限容量如表8。

表8 不同母线类型下光伏极限接入容量 MW

母线类型最大并网容量PQ90PV转PQ120PV195

对于PV节点，有足够的可调无功容量，用以维持给定的电压幅值，此时光伏可并网容量最大；若是PV转PQ类型的节点，当达到无功调整容量上限，PV节点就开始向PQ节点转化，光伏并网极限减小；当并网点为PQ节点时，其送出的功率在定时间内为定值，没有无功调节容量及对电压变化的响应能力，故最容易发生电压越限。因此，在选择光伏接入点时，从电压控制的角度，宜选择无功调节能力强的节点，同时配置自动电压调节装置，以提高系统的光伏接纳能力。

4 结束语

本文基于2个算例，通过概率密度分布、灵敏度分析、标准差分析及越限概率分析等方法从光伏接入容量、光伏接入点、多光伏电站出力相关性等方面较为全面地分析了大规模光伏并网对电力系统潮流的影响，可为电力系统新能源规划与运行提供决策参考，提出未来光伏大规模并网可能存在的问题，促进光伏并网的合理发展。

光伏接入容量过大、光伏电站出力相关性较大可能造成节点电压、支路潮流波动范围过大或越限概率超过电网运行限制，需要对光伏接入引起正向波动的节点及线路予以重点关注。从改良网损的角度而言，光伏接入点宜取重载节点，同时光伏并网容量较大时宜接入高压网通过低阻线路进行外送。从电压控制的角度，需选择无功调节能力强的节点，或配置自动电压调节装置。实际应用中应综合考虑各个影响因素，合理配置光伏电站容量，提高电网消纳间歇性电源的能力，使集中式规模化光伏发电并网能够成为现实。

[1] 任东明. “十三·五” 可再生能源发展展望[J]. 科技导报, 2016, 34(1):133-138.

[2] BALAMURUGAN K, SRINIVASAN D. Review of Power Flow Studies on Distribution Network with Distributed Generation[C]∥2011 IEEE Ninth International Conference on Power Electronics and Drive Systems (PEDS), Singapore, 2011: 411-417.

[3] 王志群，朱守真，周双喜． 分布式发电对配电网电压分布的影响[J]． 电力系统自动化，2004，28(16)：56-60．

[4] LIU L, ZHAO Y, ZHANG T Y. Study on Influence of Inserted Photovoltaic Power Station to Voltage Distributing of Distribution Network[C]∥Innovative Smart Grid Technologies-Asia(ISGT Asia)，2012 IEEE, Tianjin, China, 2012: 21-24.

[5] 丁 明，吴兴龙，陆 巍，等． 含多个不对称光伏并网系统的配电网三相随机潮流计算[J]． 电力系统自动化，2012，36(16)：47-52．

[6] 王成山，郑海峰，谢莹华，等． 计及分布式发电的配电系统随机潮流计算[J]． 电力系统自动化，2005，29(24)：39-44．

[7] 陈 炜，艾 欣，吴 涛，等． 光伏并网发电系统对电网的影响研究综述[J]． 电力自动化设备，2013，33(2)：26-32．

[8] 张文婷, 范立新. 基于直流概率潮流的风电穿透功率极限计算[J]. 江苏电机工程, 2014, 33(4): 1-4.

[9] El-MABRUK SAAD Y, PONNAMBALAM K. Stochastic Analysis of a Local Distribution Company Voltage Profile Under Uncertain Energy Supply from a Photovoltaic System[C]∥2010 7th International Conference on the European Energy Market, Madrid, Spain, 2010: 1-7.

[10] CONTI S, RAITI S. Probabilistic Load Flow for Distribution Networks with Photovoltaic Generators Part 1: Theoretical Concepts and Models[C]∥2007 International Conference on Clean Electrical Power, Capri, Italy, 2007: 132-136.

[11] RUIZ-RODRIGUEZ F J, HERNNDEZ J C, JURADO F. Probabilistic Load Flow for Radial Distribution Networks with Photovoltaic Generators[J]. IET Renewable Power Generation, 2012, 6(2): 110-121.

[12] ZHANG Z, LI G Y, WANG S, et al. Stochastic Evaluation of Voltage in Distribution Networks Considering the Characteristic of Distributed Generators[C]∥2011 4th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, Weihai, China, 2011: 1132-1137.

[13] ANANDRAJ J E. Point Estimate Method of Load Flow for Distribution Network with Photovoltaic Generators[C]∥2013 International Conference on Energy Efficient Technologies for Sustainability, Nagercoil, India, 2013: 24-29．

[14] 茆美琴，周松林，苏建徽． 基于风光联合概率分布的微电网概率潮流预测[J]． 电工技术学报，2014，29(2)：55-63．

[15] REN Z Y, YAN W, ZHAO X. Probabilistic Power Flow for Distribution Networks with Photovoltaic Generators[C]∥2013 IEEE Power and Energy Society General Meeting, Vancouver, Canada, 2013: 1-5．

[16] DONG L, LAO L Y, YANG Y H, et al. Probabilistic Load Flow Analysis Considering Power System Random Factors and their Relevance[C]∥2011 Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 2011: 1-4.

[17] 王 玮, 沈 忱. 基于改进单神经元自适应控制的光伏发电系统 MPPT 研究[J]. 江苏电机工程, 2015, 34(1): 33-35.

[18] 易桂平, 胡仁杰. 太阳能光伏电池建模与动态特性仿真[J]. 江苏电机工程, 2014, 33(5): 32-35.[19] 廖志凌，阮新波． 任意光强和温度下的硅太阳电池非线性工程简数学模型[J]． 太阳能学报，2009，30(4)：430-435．

[20] YU H，CHUNG C Y，WONG K P，et al．Probabilistic Load Flow Evaluation with Hybrid Latin Hypercube Sampling and Cholesky Decomposition[J]．IEEE Transactions on Power Systems，2009，24(2)：661-667．[21] 陈 雁，文劲宇，程时杰． 考虑输入变量相关性的概率潮流计算方法[J]． 中国电机工程学报，2011，31(22)：80-87．

[22] 石东源，蔡德福，陈金富，等． 计及输入变量相关性的半不变量法概率潮流计算[J]． 中国电机工程学报，2012，32(28)：104-113．

金 楚

金 楚(1990 —)，女，湖南双峰人，硕士研究生，研究方向为新能源发电及储能在新能源并网中的应用；

黎嘉明(1989 —)，男，广东梅州人，博士研究生，研究方向为电力系统运行与控制、新能源发电并网等；

徐沈智(1993 —)，男，安徽滁州人，硕士研究生，研究方向为综合能源网、 电力系统优化运行与控制；

文劲宇(1970 —)，男，湖南长沙人，教授，博士生导师，研究方向为电力系统运行与控制、电能存储与电力安全、大规模风电并网等。

Probabilistic Load Flow Calculation and Influence Analysis for Power Grid Connected with Large Scale Photovoltaic Generation System

JIN Chu, LI Jiaming, XU Shenzhi, WEN Jinyu,

(State Key Laboratory of Advanced Electromagnetic Engineering and Technology(College of Electrical and Electronic Engineering, Huazhong University of Science and Technology), Wuhan 430074, China)

With the increase of grid-connected photovoltaic generation capacity, the inherent characteristics of fluctuation and intermittence of the photovoltaic generation lead to the result that large-scale PV integration will change the distribution of power flow and even reverse it, influencing the stability and security of power grid. A steady-state model of PV generation system is established in the paper. Based on the IEEE 14-bus system and power grid of a province in Northwest China, probabilistic load flow calculation of power grid connected with photovoltaic generation system has been carried out. The influence of large scale grid-connected PV generation on load flow of power system is fully analyzed under the circumstances of different grid-connected capacity, different grid-connected spots and different output correlations of the PV generation system. The results indicate that the fluctuations and limit violation probabilities of power system voltage and load flow increase with the addition of PV capacity. What’s more, power loss as well as PV penetration level is influenced by grid-connected spots and the impact of PV on load flow is directional. Additionally, the correlations among PV power stations cannot be ignored. The research does provide reference for the planning and operation of power system with large integration of renewable energy.

grid-connected photovoltaic generation; probabilistic load flow; correlation

2016-10-25；

2016-11-22

国家自然科学基金项目(5157070585)；国家重点研发计划智能电网技术与装备专项项目(2016YFB0900400, 2016YFB0900403)

TM732

A

2096-3203(2017)01-0001-08