纤维弹性细杆模型几何大变形静力学分析的有限元方法

李二明，华志宏，薛文良，程隆棣

(东华大学 a． 理学院； b． 纺织面料技术教育部重点实验室， 上海 201620)

纤维弹性细杆模型几何大变形静力学分析的有限元方法

李二明a，华志宏a，薛文良b，程隆棣b

(东华大学 a． 理学院； b． 纺织面料技术教育部重点实验室， 上海 201620)

以纺织工程中的气流辅助加捻纺纱为背景，以弹性细杆为纤维模型，对其几何位移大变形的非线性问题进行分析和讨论．采用空间杆单元有限元分析方法，导出了考虑轴力对弯曲影响的空间杆单元刚度矩阵，空间方位用欧拉角表示，几何非线性采用分步加载逐次逼近方法处理，建立了弹性细杆静力平衡方程组．对纤维弹性细杆有限元总体分析，运用Matlab模拟气流辅助加捻纺纱过程中纤维包缠的平衡状态．

纤维；弹性细杆；有限元；大变形；分步加载

纺织工程各种纺纱工艺的成纱机理研究中，迫切需要了解纤维在各种复杂受力状态下的运动行为表现．纤维是一种具有一定弹性的具有超大长径比的柔性连续体材料．在以往的研究中为便于计算，通常把纤维简化为较简单的各种力学模型，例如把纤维简化为是由许多刚性短杆相互铰链串接的杆链模型[1 - 2]，这些模型与纤维的实际力学行为之间都存在着较大的失真．本文不作简化直接把纤维看作连续的弹性细杆进行计算研究．文献[3]系统地介绍了研究弹性细杆的非线性力学方法，目前都以多参数表达的联立偏微分方程组来表述弹性细杆的力学行为，较难用于一般空间三维问题的实际数值计算．本文采用空间杆单元有限元方法计算弹性细杆的空间静力学问题．通常的杆单元有限元法只能处理系统小变形的线性问题，而纺织工程中的纤维受力变形属于几何大变形非线性问题．本文推导出了同时考虑杆的拉压、弯曲和扭转并计入拉压轴力对弯曲影响的空间杆单元刚度矩阵，对于几何大变形非线性问题采用分步加载逐次逼近的方法进行计算，并以此方法计算了气流辅助加捻纺纱过程中纤维包缠状态分析．

1 空间杆单元刚度矩阵

杆单元在三维空间的变形可分解为轴向拉压变形、两个主平面内的弯曲变形和扭转变形的组合．当弹性细杆发生几何大变形或轴力较大时，必须考虑轴力对弯曲变形的影响．

1.1 单元的杆端位移和杆端力

将整个空间弹性细杆划分成若干微小杆单元．为整个弹性细杆建立一个总体坐标系O -xyz，再为每个杆单元建立一个单元局部坐标系O′-uvw，如图1所示．其u轴为杆单元的轴线方向，uO′v和uO′w为杆单元的两个弯曲主平面方位．

图1 空间杆单元及其坐标系Fig.1 The spatial bar element and coordinate system

杆单元e节点i和节点j的杆端位移可以表示为

Δuj,Δvj,Δwj,Δθuj,Δθvj,Δθwj}T

(1)

式中：Δui, Δvi, Δwi和Δuj, Δvj, Δwj为节点线位移；Δθui, Δθvi, Δθwi和Δθuj, Δθvj, Δθwj为横截面角位移．

与杆端位移对应的杆端力可表示为

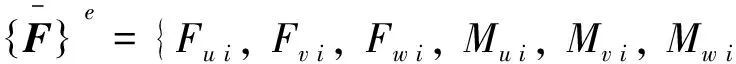
Fu j, Fv j, Fw j, Mu j, Mv j, Mw j}T

(2)

式中：Fu i, Fv i, Fw i和Fu j, Fv j, Fw j为节点力；Mu i, Mv i, Mw i和Mu j, Mv j, Mw j为节点力偶．

1.2 杆单元的弯曲变形分析

分析图2所示uO′v平面内的弯曲变形．考虑杆的轴力对弯矩的影响，杆单元任意截面位置u的弯矩为

M=Fv iu+Fn(v-Δvi)-Mw i

(3)

式中：v为杆的挠度；Fn为杆的轴力，Fn=-Fui=Fuj．假设杆单元的刚性位移远大于其弹性变形，式(3)中的v近似取

(4)

式中：l为杆单元长度．式(4)代入式(3)得

(5)

图2 主平面内的弯曲变形Fig.2 Bending deformation in the principal plane

假设相对于局部坐标系O′-uv，杆单元的位移为小量，其挠曲线的一阶导数很小，则杆的弯曲挠曲线近似微分方程[4]为

(6)

式中：Iw为截面惯性矩；E为材料弹性模量．式(5)代入式(6)得

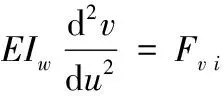
(7)

通过对u积分，并根据杆单元节点边界条件及其杆单元力平衡方程可解得

(8)

同理，在uO′w平面内的弯曲变形也可导出类似的杆端力与杆端位移关系．

1.3 杆单元的刚度矩阵

对于杆的轴向拉压变形和扭转变形，可导出下列关系

(9)

(10)

式中：A为横截面面积；G为材料剪切弹性模量；Ip为截面极惯性矩．

(11)

而空间杆单元的杆端力和杆端位移关系可简写为

(12)

2 坐标变换

2.1 刚度矩阵的坐标变换

在图1所示总体坐标系中，单个节点的位移为沿x、y、z轴的线位移和绕x、y、z轴的角位移，杆单元的杆端位移和杆端力为

{Δ}e={ Δxi, Δyi, Δzi, Δθxi, Δθyi, Δθzi,

Δxj, Δyj, Δzj, Δθxj, Δθyj, Δθzj}T

(13)

Fxj, Fyj, Fzj, Mxj, Myj, Mzj}T

(14)

在总体坐标系O-xyz和局部坐标系O′-uvw之间存在如下坐标变换

(15)

其中

(16)

为杆单元e的单元坐标变换矩阵，而

(17)

为单元局部坐标系O′-uvw相对于总体坐标系O-xyz的方向余弦矩阵．

(18)

其中

(19)

即为杆单元相对于总体坐标系的刚度矩阵．

2.2 坐标系方位的欧拉角坐标表示

如图3所示，将单元局部坐标系O′-uvw的方位看作是坐标系O-xyz依次绕图中z轴、x1轴和z2轴的3个转动角ψ1、 ψ2和ψ3实现的．(ψ1, ψ2, ψ3)通常被称为欧拉坐标．以欧拉角表示的坐标方向余弦矩阵[5]如下

(20)

图3 欧拉角Fig.3 Euler’s angles

(21)

(22)

3 非线性问题的分步加载计算法

3.1 分步加载逐次逼近概念

纤维弹性细杆模型超大位移变形问题为几何非线性问题．由式(12)或式(18)表示的单元刚度方程只有在杆单元相对于单元局部坐标系的位移足够小的情况下才成立．为此，必须保证杆单元的长度足够的小，杆单元的局部坐标系的位置距离弹性细杆大位移变形后的精确位置足够的近．

现采用载荷分步加载逐次逼近的方法求解．载荷从零开始由小到大分若干次逐渐加大进行分步计算，并保证每一步载荷的增量为一小量．在每步计算中，都以上一步的载荷作用下求得的位置精确值，作为求解下一步的载荷作用下的位置精确值的初始近似值，来求解下一步位置的精确值．对于载荷为零开始的第一加载步计算，将整个弹性细杆无载荷状态的位置作为初始位置，在该位置为每个杆单元建立单元局部坐标，然后载荷增加一个小量，用相对于单元局部坐标小位移情况下成立的单元刚度方程求解在该载荷作用下的各杆单元的位移，从而得到整个弹性细杆变形后的位置；对于任意第N+1加载步计算，将第N步求得的弹性细杆位置作为初始位置，在该位置再为每个杆单元建立单元局部坐标，将载荷在第N步的基础上再增大一个小量，继续用相对于单元局部坐标小位移情况下成立的单元刚度方程式求解在该新的载荷作用下的各杆单元的位移，从而得到整个弹性细杆的一个新的位置．

3.2 逐次逼近计算式

考察图4所示的一个加载步中的任意某个单元．图4中i -j位置为该加载步初始位置，i′-j′位置为载荷增大一小量后单元的新位置，i -j0位置为杆单元无受力变形的位置，坐标面vO′w位于单元i端的横截面上， Δri和Δrj为该单元的位移增量．

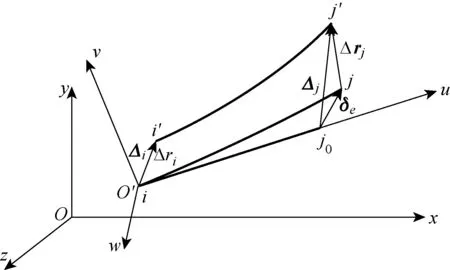
图4 单元分步加载分析Fig.4 Step loading analysis of the unit

由图4可看出

(23)

其中，相对于总体坐标系O-xyz

上述每个位移量中均包含线位移分量和角位移分量．而单元杆端位移

(24)

将式(24)代入单元刚度方程式(18)，得每一加载步的单元位移增量方程如下

(25)

其中

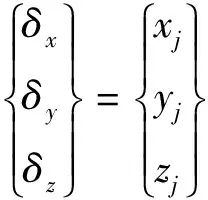
4 有限元总体分析

4.1 整体位移增量方程

如图5所示，一空间弹性细杆被划分为n个杆单元，共有n+1个节点，每个节点有6个自由度，全部节点共有6(n+1)个自由度，即共有6(n+1)个位移分量．

图5 杆的单元分解Fig.5 The element dividing of the rod

对于由式(25)表示的每个单元e的单元位移增量方程，相对于总体节点自由度，可改写成如下维数矩阵

(26)

将图5所示的全部单元组合在一起，其全部节点的静力学平衡方程为

(27)

将式(26)代入式(27)，得

或简写成如下形式

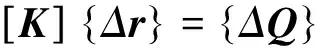
(28)

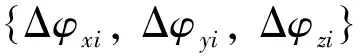
4.2 算例

将纺织工程中气流辅助加捻纺纱过程简化成图6所示力学模型．图6中大圆柱体CD代表中心须条，看作相对固定的刚体．弹性细杆AB代表一根包缠纤维，在由绕中心须条旋转的气流场产生的空气阻力q作用下包缠到中心须条上．现把弹性细杆A端的约束看作固定约束，把空气阻力看作弹性细杆所受的载荷，分析计算纤维在给定载荷作用下包缠在中心须条上的静平衡形态．

图6 气流辅助加捻纺纱的力学模型Fig.6 Mechanical model of airflow assisted twisting yarn

采用杆单元有限元法，将整个弹性细杆均分成n个单元．对于气流作用于杆的分布载荷，在计算时将其向各节点简化．关于弹性细杆与中心刚性圆柱之间的接触约束，采用罚函数法处理，即在两者之间构造一个排斥力，该力在两者之间的距离较接近时快速增大，而存在一定距离后就快速衰减到零，从而在分步加载逼近过程中阻止弹性细杆进入中心刚性圆柱体内．

运用Matlab编程计算，代入具体数据，求得纤维包缠的静平衡形态如图7所示．

(a) 空间三维视图

(b) yz平面视图图7 纤维包缠的静平衡形态Fig.7 The static equilibrium configuration of the fiber wrapping

5 结 语

本文采用空间杆单元有限元方法研究了纤维弹性细杆几何大变形静力平衡状态，直接对纤维弹性细杆几何大变形进行数值求解，得到纤维在气流作用下包缠在中心刚性圆柱上的静平衡位置形态， 解

决了杆单元有限元分析方法难以用于空间三维几何大变形问题实际计算的问题．改变数值模拟原始条件，可以得出不同载荷作用下纤维弹性细杆包缠须条的状态，为气流辅助加捻纺纱设备的设计与改进提供了理论基础，同时也为纤维弹性细杆几何大变形动力学分析提供了基础和方向．

[1] 郭会芬．喷气纺纱喷嘴内三维旋转气流场及柔性纤维运动的研究[D]．上海：东华大学纺织学院，2009：110111．

[2] KONG L X, PLATFOOT R A. Computational two-phase air/fiber flow within transfer channels of rotor spinning machines [J]. Textile Res J, 1997, 67(4): 269278.

[3] 刘延柱．弹性细杆的非线性力学[M]．北京：清华大学出版社，2006：1452．

[4] 刘鸿文．材料力学[M]．5版．北京：高等教育出版社，2011：174177．

[5] 洪嘉振．计算多体系统动力学[M]．北京：高等教育出版社，1999：4647．

Finite-Element Method of Statics Analysis of the Geometric Large Deformation of Fiber Elastic Thin Rod Model

LI Er-minga，HUA Zhi-honga， XUE Wen-liangb， CHENG Long-dib

(a． College of Science； b． Key Laboratory of Textile Science & Technology， Ministry of Education，Donghua University， Shanghai 201620， China)

Based on the airflow assisted twisting of yarn spinning in the textile engineering, using the elastic thin rod as the fiber model, the geometric nonlinear problems for this model’s large deformation were analyzed and discussed. Using finite-element method and taking the bending problem influenced by the axial force into consideration, the spatial bar element stiffness matrixes were derived. The elastic thin rod static equilibrium equations were established using consecutive loading approach to deal with geometric nonlinearity problem and using Euler’s angle to denote spatial orientation. The unity of the fiber elastic thin rod was analyzed by the finite-element method,and the static equilibrium configurations of the fiber in the airflow assisted twisting yarn for textile engineering were simulated by Matlab.

fiber; elastic thin rod; finite-element; large deformation; consecutive loading

16710444 (2016)060916-06

20150914

上海市自然科学基金资助项目(13ZR1400900)

李二明(1986—)，男，河南驻马店人，硕士研究生，研究方向为固体力学．E-mail: 2131410@mail.dhu.edu.cn 华志宏(联系人)，男，副教授，E-mail: hzh@dhu.edu.cn

TS 101.2

A