关于蕴含Ramsey数rpot(Kn-ke,Kt-qe)问题

马珩博，尹建华

(海南大学 信息科学技术学院，海南 海口 570228)

关于蕴含Ramsey数rpot(Kn-ke,Kt-qe)问题

马珩博，尹建华

(海南大学 信息科学技术学院，海南 海口 570228)

蕴含Ramsey数； 可图序列； 实现

1 引言

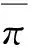
定理1[3]若G是一个n阶无孤立点的图G满足α(1)(1)≤n-1，且t≥2，则

rpot(G,Kt)≥max{2t+n-α(1)(G)-2,n+t-2} .

定理2[3]对于n≥t≥3，rpot(Kn，Kt)=2n+t-4，除了当n=t=3时，rpot(K3，K3)=6.

根据定理2，容易得到以下结论：若A和B分别是4阶以上的完全图C和D的子图，则

rpot(A,B)≤rpot(C,D)=max{|C|,|D|}+|C|+|D|-4.

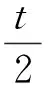
一个图G的2-独立数，记为α(2)(G)，是G的一个导出子图H的最大阶数且满足H的最大度Δ(H)≤2 .

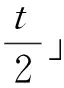
rpot(G,Kt-ke)≥2t+n-α(2)(G)-k-1.

根据定理3，容易得到关于rpot(Kn-ke,Kt-qe)的下界推论.

推论1 当n,t≥5时，

rpot(Kn-ke,Kt-qe)≥max{2t+n-x(k)-q,2n+t-x(q)-k},

其中,当s=0或1时x(s)=4，当s≥2时x(s)=5.

根据定理2和推论1，有以下

推论2 若n≥t≥4，则rpot(Kn，Kt-e)=2n+t-4.

推论3 若n≥t≥4，则2n+t-5≤rpot(Kn-e,Kt-e)≤2n+t-4.

2 定理3的证明

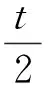
引理1得证.

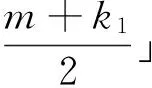
引理2得证.

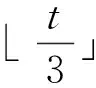
推理4得证

推论5得证.

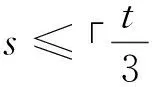
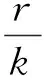
引理3得证.

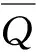
推论6得证.

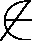
引理4得证.

定理3的证明 考虑可图序列π=((2t+n-α(2)(G)-k-3)n-a(2)(G)-1，(n-α(2)(G)+1)2t-k-1).易见，π的实现为Kn-α(2)(G)-1∨S，其中∨表示联图，S为一个2t-k-1阶正则图.假设Kn-α(2)(G)-1∨S包含G作为子图,则G中有至少α(2)(G)+1个顶点落在S中,从而G的2-独立数至少为α(2)(G)+1，不可能.故π不是蕴含G可图的.

综上所述，rpot(G,Kt-ke)>2t+n-α(2)(G)-k-2.由于rpot(G,Kt-ke)是一个正整数，所以rpot(G,Kt-ke)≥2t+n-α(2)(G)-k-1.

定理3的得证.

[1] Yin J H,Li J S. Two sufficient conditions for a graphic sequence to have a realization with prescribed clique size[J]. Discrete Mathematics，2005(301):218-227.

[2] Yin J H.A characterization for a graphic sequence to be potentially Gr-graphic[J].Science China Mathematics,2010(11):2 893-2 905.

[3] Busch A ，Ferrara M ，Hartke S G， et al. A degree sequence variant of graph Ramsey number[J]. Graphs and Combinatorics，2014(30):847-859.

Problem of Potentially Ramsey Number rpot(Kn-ke,Kt-qe)

Ma Hengbo, Yin Jianhua

(College of Information Science and Technology, Hainan University, Haikou 570228, China)

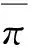
potentially Ramsey Number; graphic sequences; realization

2016-07-01

海南省自然科学基金(2016CXTD004)

马珩博(1993-)，男，山西大同人，海南大学2015级硕士研究生，研究方向：蕴含Ramsey数，E-mail：1693951315@qq.com

尹建华(1970-)，男，湖南祁阳人，教授，博士，研究方向：图论及其应用，E-mail: yinjh@hainu.edu.cn

1004-1729(2016)04-0319-05

O 157.5

A DOl：10.15886/j.cnki.hdxbzkb.2016.0048