一类广义中立型Emden-Fowler方程的振动准则

惠远先，王俊杰

(普洱学院 数学系，云南 普洱 665000)

一类广义中立型Emden-Fowler方程的振动准则

惠远先，王俊杰

(普洱学院 数学系，云南 普洱 665000)

研究了一类广义中立型Emden-Fowler 方程的振动性质，通过构造广义Riccati变换得到了广义Riccati不等式，用积分平均技巧等方法，建立了保证方程一切解振动或者收敛到零的若干新的充分条件，所得结论推广和改进了最近文献中的若干结果，最后给出了若干例子来验证工作的有效性.

广义中立型Emden-Fowler方程； 广义Riccati变换； 振动准则

微分方程的振动理论是微分方程定性理论的一个重要分支.随着科技的迅速发展，在控制工程、生物制药、机械振动和力学等应用领域中的的很多实际问题中均出现了微分方程是否存在振动解或者微分方程的一切解是否均为振动的问题.

20世纪八十年代以来，微分方程的振动理论得到了迅速地发展.从线性到半线性、超线性和非线性，从一阶到二阶、三阶、偶数阶和n阶，从纯量方程到矩阵方程，从连续方程到离散方程、时间尺度上的动力方程，都取得了丰富的研究成果.

由于二阶动力方程的力学意义非常明显，因而研究比较深入和广泛，无论从方程的类型还是从研究的方法上都取得了长足的发展.目前振动理论常用的研究方法有Riccati变换、变分原理和积分平均技巧等，由于积分平均方法巧妙地避免了对动力方程系数函数的限制，扩大了结果的应用范围，因此广受研究者青睐.

考虑一类广义中立型Emden-Fowler方程

[r(t)|Z′(t)|α-1Z′(t)]′+∫abq(t,ξ)|x(δ(t,ξ))|β-1x(δ(t,ξ))dσ(ξ)=0 t≥t0

(1)

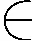
1) α>0,β>0;

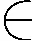
3) r(t)≥0,r′(t)≥0,∫t0∞r-1/α(s)ds=+∞；

近年来，由于在物理学和工程技术等领域的广泛应用，Emden-Fowler方程的振动理论引起了国内外学者的广泛关注，产生了大量优秀的成果，详见文献[1-12].1983年，Philos[1]建立了经典的Emden-Fowler方程

x″(t)+q(t)|x(t)|β-1x(t)=0

的一些振动准则；1986年，Yan[2]建立了经典的Emden-Fowler阻尼方程

x″(t)+g(t)x′(t)+q(t)|x(t)|β-1x(t)=0

的一些振动准则；2006年，Meng[3]给出了广义Emden-Fowler方程

[r(t)|x′(t)|α-1x′(t)]′+q(t)|x(δ(t))|α-1x(δ(t))=0

的振动结果；2012年,Liu[12]利用广义黎Ricaaati变换给出一类广义Emden-Fowler方程

[r(t)|Z′(t)|α-1Z′(t)]′+q(t)|x(δ(t))|β-1x(δ(t))=0 t≥t

(2)

在α≥β>0情形下的振动准则，由于条件α≥β>0的限制，得到的振动结果具有很大局限性.目前，对广义中立型Emden-Fowler方程(1)的研究还比较少.

通过构造广义Riccati变换和积分平均技巧得到了一类中立型广义Emden-Fowler方程(1)的若干新的振动准则，不仅将文献[12]的条件由α≥β>0推广到α>0，β>0而且将方程(2)推广到了更一般的方程(1)，具有重要的意义.

1 引理

引理1 设是广义中立型Emden-Fowler方程(1)的正解，则Z′(t)>0.

证明设x(t)是方程(1)的正解，则Z(t)≥x(t)>0，由方程(1)得

[r(t)|Z′(t)|α-1Z′(t)]′=-∫abq(t,ξ)|x(δ(t,ξ))|β-1x(δ(t,ξ))dσ(ξ)≤0,

所以r(t)|Z′(t)|α-1Z′(t)最终定号，Z′(t)有2种情况，Z′(t)>0或者Z′(t)<0.

假设Z′(t)<0，由于[r(t)|Z′(t)|α-1Z′(t)]′≤0，则存在一个充分大的数t1>0及K>0使得

r(t)|Z′(t)|α-1Z′(t)=-r(t)[-Z′(t)]α≤-r(t1)[-Z′(t1)]α=-K t>t1> t0，

对上式从t1到t积分，可以得到

令t→+∞，利用3)，得到Z(t)→-∞，与Z(t)>0相矛盾，从而Z′(t)>0成立.

引理2 设x(t)是广义中立型Emden-Fowler方程(1)的正解，则

[r(t)|Z′(t)α]′+Q1(t)Zβ(δ(t，a))≤0，

(3)

其中，Q1(t)=∫abq(t,ξ)[(1-p(δ(t,ξ)))]βdσ(ξ).

证明设x(t)是方程(1) 在[t0,+∞]上的正解，由Z(t)的定义，可得x(t)=Z(t)-p(t)x(τ(t))，利用4)，5)和Z′(t)>0，则

x(δ(t,ξ))=Z(δ(t,ξ))-pδ(t,ξ)x(τ(δ(t,ξ)))≥Z(δ(t,ξ))(1-ρ(δ(t,ξ))),

xβ(δ(t,ξ))≥Zβ(δ(t,ξ))(1-p(t,ξ)))β≥Zβ(δ(t,a))(1-ρ(δ(t,ξ)))β,

从而

∫abq(t,ξ)|x(δ(t,ξ))|β-1x(δ(t,ξ))dσ(ξ)=∫abq(t,ξ)xβ(δ(t,ξ))dσ(ξ)≥ ∫abq(t,ξ)(1-ρ(δ(t,ξ)))βdσ(ξ)Zβ(δ(t,a))，

利用方程(1)，可以得到

[r(t)Z′(t)α]′+Q1(t)Zβ(δ(t,a))≤0 .

引理3[4]设存在2个函数A(θ)>0,B(θ)>0 且 θ>0，则

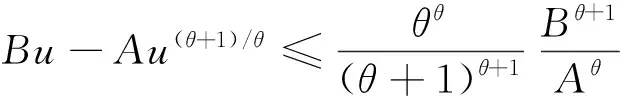
(4)

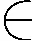
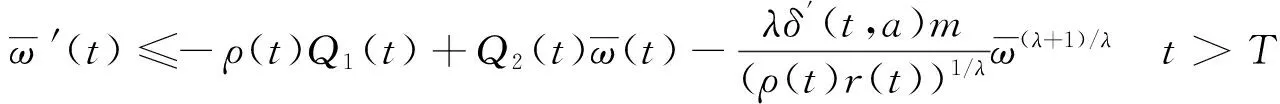
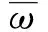
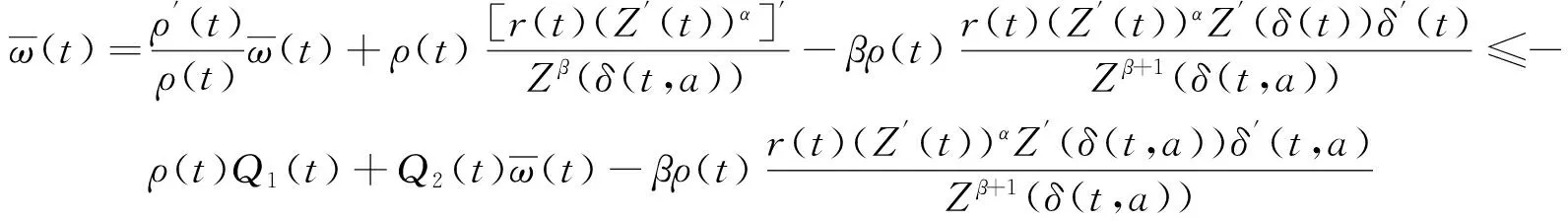
1) β>α>0时，

由引理2知，[r(t)(Z′(t))α]′≤-Q1(t)Zβ(δ(t,a))≤0，所以，r(t)Z′(t)α单调递减，

r(t)(Z′(t))α≤r(δ(t,a))(Z′(δ(t,a)))α，

Zβ/α-1(δ(t,a))≥Zβ/α-1(δ(T1,a)) t≥T1，

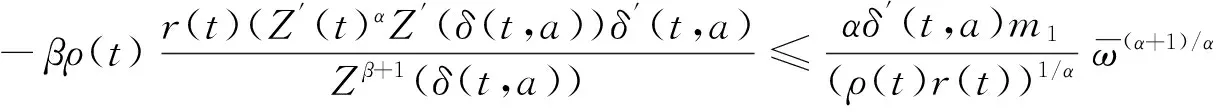
β>α>0时

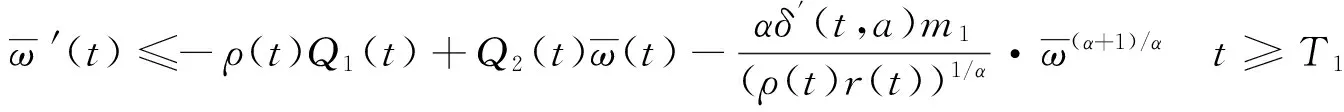
(5)

2) α≥β>0时，

.

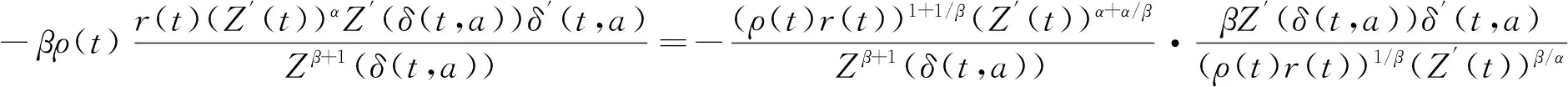
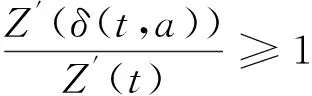
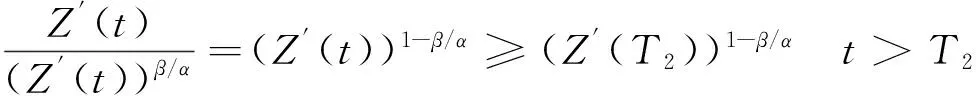
记m2=min{1,(Z′(T2))1-β/α}，则

从而

(6)

现记T=max{T1，T2}，λ=min{α,β}，所以综合式(10)和(11)可得α>0，β>0时的广义Riccati不等式为

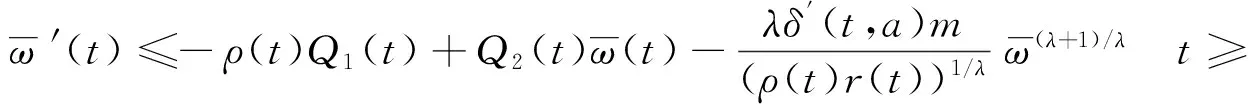
(7)

2 主要结果

定理1假定1)～5)成立，x(t)是方程(1)的解，若

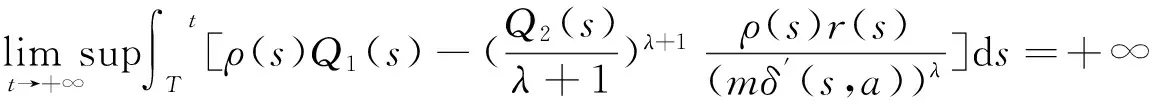
(8)

则方程(1)是振动的.

证明假设x(t)是方程(1)的非振动解，由于x(t)=0无实际意义，仅考虑x(t)≠0的情形，不失一般性，设x(t)是方程(1)的正解，由引理4得式(7)， 由引理3得

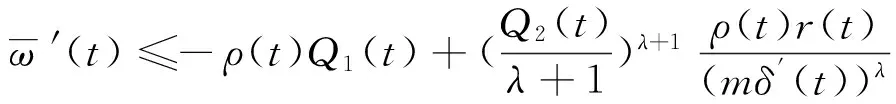
对上式从T到t积分可得

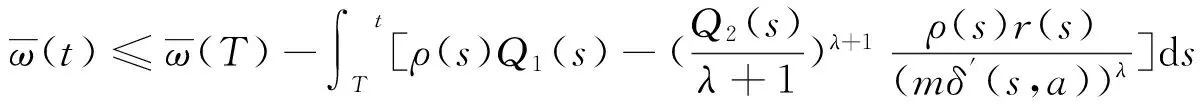
假定ρ(t)=δ(t,a)，则定理1可得以下推论

推论1 假定1)～5)成立，x(t)是方程(1)的解，则若

则方程(1)是振动的.

给出广义中立型Emden-Fowler方程(1)的振动准则,为此令

D0={(t,s):t>s≥t0},D0={(t,s):t≥s≥t0}

1) H(t,t)=0 t≥t0，H(t,t)>0 D；

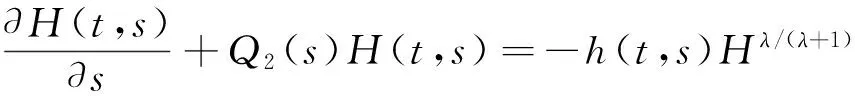
(9)

定理2假设1)～5)成立，x(t)是方程(1)的解，如果

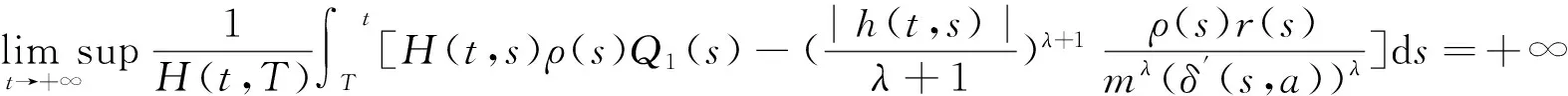
(10)

则方程(1)是振动的.

证明假设x(t)是广义中立型Emden-Fowler方程(1)的非振动解，不失一般性，设x(t)是方程(1)的正解，由引理4得

两边同乘以H(t,s)，并从T到t(t>T)两边积分，再由引理3及方程(9)得

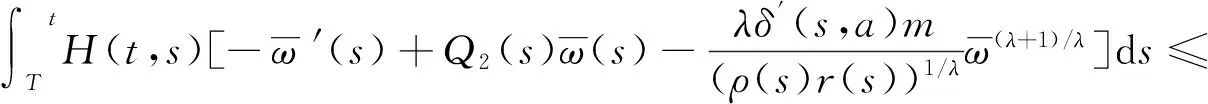
(11)

由方程(11)可得

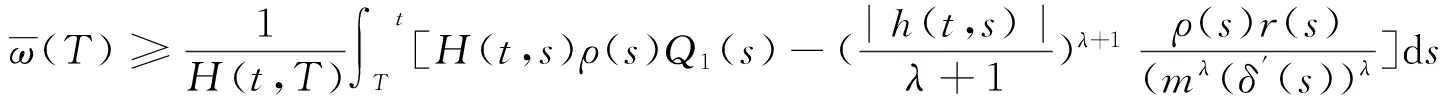
(12)

与式(10)矛盾，故原假设不成立，所求得证.

若取H(t,s)=(t-s)n，则定理1可简化为Kamenev型结果如下

推论2 假设1)～5)成立，H(t,s)=(t-s)n,x(t)是方程(1)的解,如果

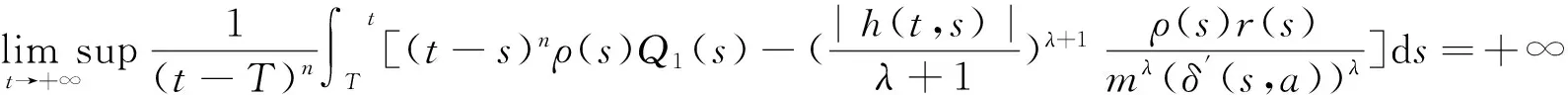
则广义中立型Emden-Fowler方程(1)是振动的.

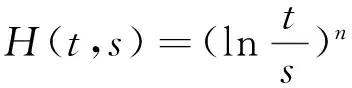
则方程(1)是振动的.

定理3假设1)～5)成立，x(t)是方程(1)的解，如果,

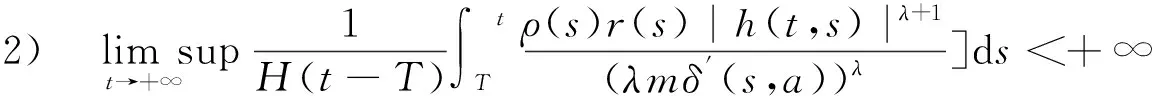
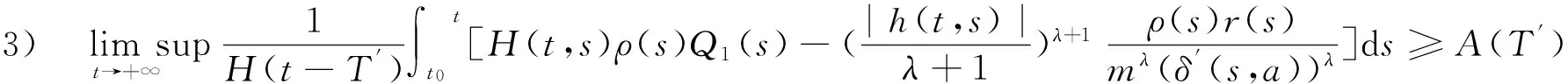
其中，T′>T>t0>0 ；

证明假设x(t)是方程(1)的非振动解，不失一般性，设x(t)是方程(1)的正解，用定理1相同的证明过程可以得到方程(11)，由此可得

利用3)可得

(13)

利用方程(11)及3)可得

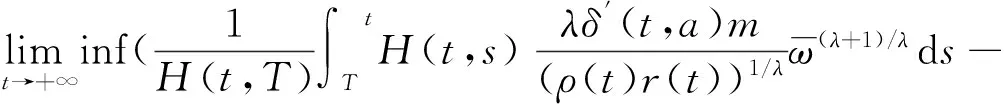
(14)

令

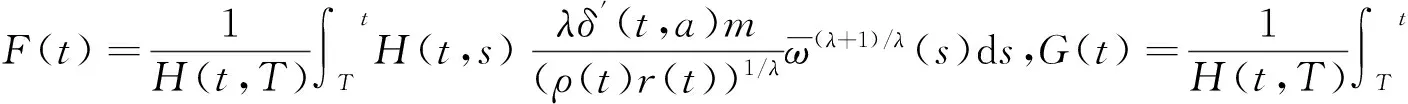
则由式(14)可得

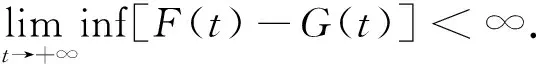
(15)

1)假设

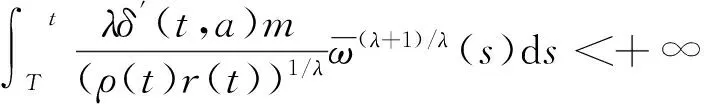
(16)

则由式(13)

与4)矛盾.所以式(16)不成立.

2) 假设

(17)

设η是一个充分小的正数，利用1)可得

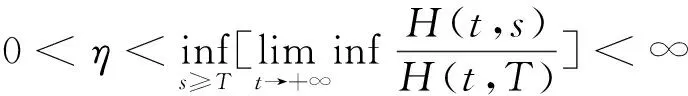
(18)

由式(17)可得，对任意大的正数μ>0

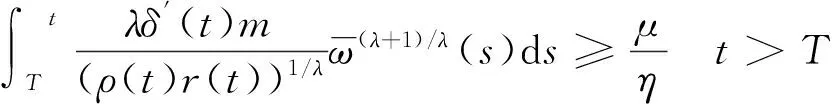
(19)

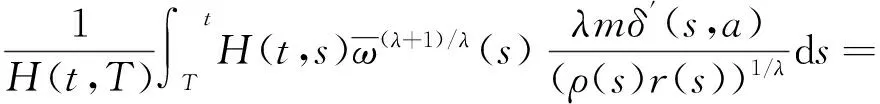
(20)

由于μ为任意大的正数，根据式(15)和(20)可得

(21)

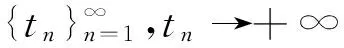
F(tn)-G(tn)≤M, G(tn)-F(tn)≥-M，

两边同除以F(tn)可得得t充分大时

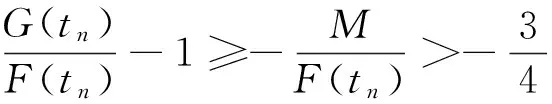
由式(21)得

两边同除以F(tn)可得

利用2)可得

(24)

与方程(22)矛盾.因此假设式(17)不成立.

综合1)和2)的证明，由于方程(16)与(17)均不成立，所以原假设不成立，从而x(t)振动，所求得证.

3 举 例

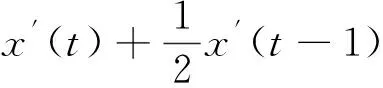
(25)

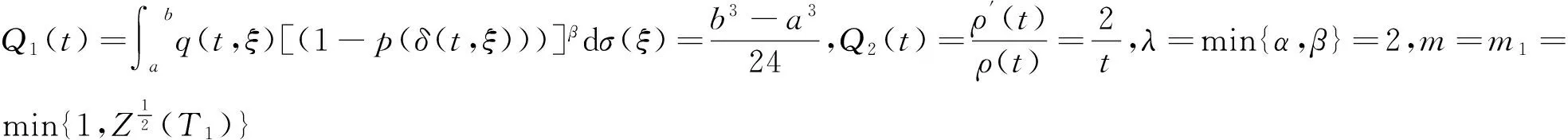
由定理1可知，方程(25)是振动的.

注1 由于方程(25)中β=3，α=2，不满足文献[12]的条件，所以利用文献[12]的相关结论无法得到方程(25)的振动性.

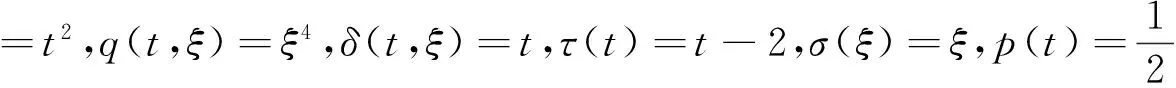
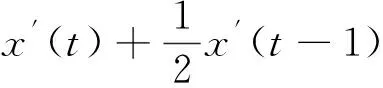
(26)

取ρ(t)=1，H(t,s)=(t-s)2，则

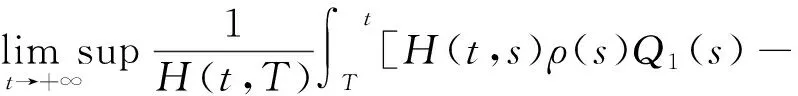
由定理2可知，方程(26)是振动的.

注2 显然例2的结论无法由文献[12]的相关结论得到.

[1] Philos C G.On a Kamenev’s integral crierion for oscillation of linear differential equations of second order[J].Utilitas Math,1983,24:277-289.

[2] Yan J. Oscillation theorems for second order linear differential equations wih damping[J].Proceedings of the American mathematical society,1986,98(2):276-282.

[3] Yuan G S, Fan W M. Note on the paper of Dzurina and stavroulakis[J].Applied Mathematics and computation,2006,174(2):1 634-1 641.

[4] Run X, Fan W M.Some new oscillation criteria for secondorder quasi-linear neutral delay differential equations[J].Applied Mathematics and computation,2006,182(1):797-803.

[5] Run X, Fan W M. Oscillation criteria for second-order quasi-linear neutral delay differential equation [J].Applied Mathematics and computation,2007,192(1):216-222.

[6] Liu L H, Bai Y C. New oscillation criteria for second order nonlinear neutral delay differential equation[J].Journal of Computational and Applied Mathematics，2009,231(2):657-663.

[7] Wong J S W. A Nonoscillation theorem for Emden Fowler equations[J]. Journal of Mathematical Analysis and Applications, 2002,274(2):746-754.

[8] Wong J S W. A nonoscillation theorem for sublinear Emden Fowler equations[J]. Analysis and Applications 2011,1(1):71-79.

[9] Kwong M K, Wong J S W. A nonoscillation theorem for sublinear Emden Fowler equations[J]. Nonlinear Anal, 2006,64(7):1 641-1 646.

[10] Li T X, Han Z L, Zhang C H, et al. On the oscillation of second-order Emden Fowler neutral differential equations[J]. Journal of Applied Mathematics and computation,2011,37(1/2):601-610.

[11] 李同兴，韩振来，张承慧,等.时间尺度上三阶Emden-Fowler时滞动力方程的振动准则[J].数学物理学报，2012，32(1)：222-232.

[12] Liu H D,Fan W M,Liu P C. Oscillation and asymptotic analysis on a new generalized Emden Fowler equation[J].Applied Mathematics and computation,2012,219(5):2 739-2 748.

Oscillation Criterion of A Generalized Emden-Fowler Equation

Hui Yuanxian, Wang Junjie

(Mathematics Department, Puer University, Puer 665000, China)

In our report, the oscillation properties of a generalized neutral Emden-Fowler equation were analyzed. The generalized Riccati inequality was obtained by constructing the generalized Riccati transformation. The integral averaging technique was used to construct some new sufficient criterias which ensure that any solution of this equation will be oscillatory or conerge to zero. The conclusions extended and improved the results in recent literatures, and a number of examples were used to prove the efficiency.

a generalized neutral Emden-Fowler equation; generalized Riccati transformation; oscillation criteria

2016-04-13

云南省教育厅基金(2015Y490)；普洱学院科研创新团队(2015CXTD003)；普洱学院校级课题(2015xjkt020)

惠远先(1983-)，男，河南南阳人，讲师，硕士，研究方向：微分方程、数学模型，E-mail：huiyuanxian1983@126.com

1004-1729(2016)04-0330-08

O 29

A DOl：10.15886/j.cnki.hdxbzkb.2016.0050