一类非线性方程组的无导数投影法的收敛速度分析

李靖雅，欧宜贵

(海南大学 信息科学技术学院，海南 海口 570228)

一类非线性方程组的无导数投影法的收敛速度分析

李靖雅，欧宜贵

(海南大学 信息科学技术学院，海南 海口 570228)

在局部误差界条件下，分析了一类非线性方程组的无导数投影法的收敛速度，证明了序列{dist(xk,X*)}Q-线性收敛于0，从而序列{xk}R-线性收敛于x*；对更一般的4种方法进行了讨论，分别得到了其收敛速度.

非线性方程组； 无导数法； 投影法； 收敛速度

本文考虑如下的非线性方程组问题

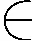
(1)

其中,X是Rn空间中的一个非空闭凸集，F：Rn→Rn是连续的映射，且满足下列特性

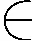
(2)

其中，X*是问题(1)的解集，本文假设X*非空. 为方便起见，在迭代点xk处，本文以下用‖·‖表示Rn中Euclidean范数，用Fk表示函数值F(xk).

无导数投影法是一类求解非线性方程组问题的有效方法. 对问题(1)，文献[1]提出了一种无导数投影法(DFPA)，详细的算法描述如下

DFPA算法

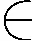
Step 2计算Fk, 若‖Fk‖≤ε，停止计算；

Step 3利用递推公式构造搜索方向dk，

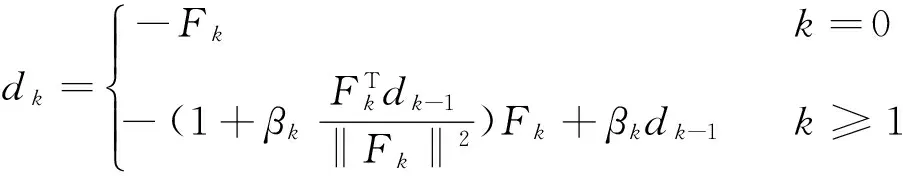
(3)

其中，βk满足条件

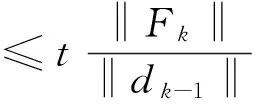
(4)

Step 4计算试验点zk=xk+αkdk，其中αk=βρlk，这里lk是满足下列线搜索方案的最小非负整数l，

-F(xk+βρldk)Tdk≥σβρl‖dk‖2；

(5)

Step 5利用迭代式

xk+1=PX[xk-ξk(vFk+F(zk))],

(6)

计算新的迭代点xx+1，其中

Step 6令k：=k+1，转Step 1.

文献[1]分析了DFPA算法的整体收敛性. 数值试验结果及其相关的一些比较表明：DFPA算法是求解大规模非线性方程组问题的一种比较有效的方法.但是文献[1]并未对DFPA算法的收敛速度从理论上进行讨论.事实上，其他关于非线性方程组的无导数投影法也尚未分析其收敛速度，请参考文献[2-3].

在局部误差界的条件下，Yamashita和Fukushima[4]于2001年证明了求解无约束非线性方程组的Levenberg-Marquardt(LM)方法具有局部超线性或二阶的收敛性，同时还指出，局部误差界条件要比非奇异性条件弱. 随后，这一条件被许多学者用来研究某些优化方法的局部收敛率问题，参考文献[5-9].

基于上述讨论并受文献[4-5]的思想启发，笔者在局部误差界等适当的假设条件下，给出了文献[1]所提出的DFPA算法具有线性收敛速度，并对更一般的情形进行了一些讨论.

1 预备知识

本节给出对后面讨论有用的定义和结果，可参考文献[1,4-5].

定义1设N是Rn空间中的一子集，且满足N∩X*≠Ø，称‖F(x)‖在N内对问题(1)提供了一个局部误差界，若存在正常数c>0，使得

(7)

定义2设Ω是Rn空间中的一非空闭凸子集，则从Rn到Ω的投影PΩ[x]定义为

(8)

注1 定义2中的投影PΩ[x]具有非扩张性[1]，即

(9)

显然，由式(3)和(4)定义的搜索方向dk具有下列特性，详见文献[1]中的Remark2.1.

引理1 DFPA算法构造的搜索方向dk满足

(10)

及

‖Fk‖≤‖dk‖≤(1+2t)‖Fk‖ ∀k.

(11)

1) 对任意的k，有

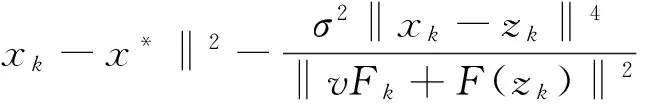
(12)

2) 序列{‖xk‖}和{‖zk‖}均有界；

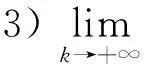
注2 引理2的证明同文献[1]中引理1.2的证明，本文在此略去.

2 DFPA算法的收敛速度分析

本节将从理论上分析DFPA算法的收敛速度,为此，需要如下假设：

假设1 映射F在非空的闭凸集X内Lipschitz连续，即存在Lipschitz常数L>0，使得

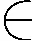
(13)

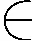
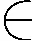
(14)

引理3 假设1成立，则存在常数γ>0，使得DFPA算法由线搜索方案(5)所确定的步长αk满足

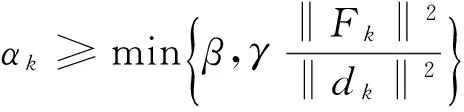
(15)

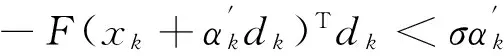
利用上式，并结合式(10)和假设1，可以推出

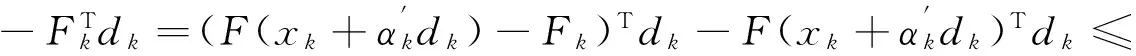
为了分析DFPA算法的收敛速度，还需要其整体收敛性结论，详见文献[1]中的Theorem2.1.

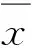
利用上述结论，分析DFPA算法的收敛速度，在一定的条件下，可以得到下列结果.

定理2设{xk}是DFPA算法产生的序列，则在假设1和假设2满足的条件下，序列{dist(xk,X*)}Q-线性收敛于0，从而序列{xk}R-线性收敛于x*.

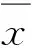
(16)

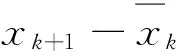
(17)

显然，利用式(11)和(15)可推知存在常数c1>0，使得

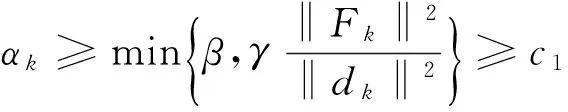
(18)

‖xk-zk‖=αk‖dk‖≥c1‖Fk‖≥c1c0dist(xk,X*)=c2dist(xk,X*),

(19)

其中c2=c1c0.同时，由式(11)，(16)，假设1和αk≤β，∀k，即得

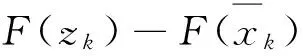
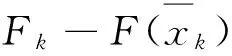
(20)

以及

(21)

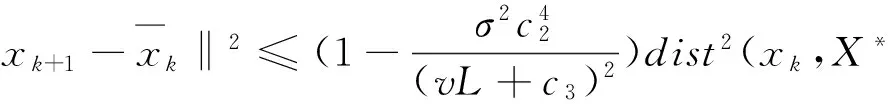
上式表示序列{dist(xk,X*)}Q-线性收敛于0，从而序列{xk}R-线性收敛于x*.

3 进一步的讨论

从以上分析可以看出搜索方向dk的构造对DFPA算法的收敛速度具有重要作用. 实际上，dk还有其他的构造方法，只要其满足下列方向假设(参考文献[10])：存在常数μ1>0和μ2>0，使得

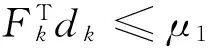
(22)

及

‖dk‖≤μ2‖Fk‖ ∀k ,

(23)

在采用相同的线搜索方案(5)的情形下，则得到求解问题(1)的相应算法仍然与DFPA算法具有相同的收敛特性，下面给出的集中构造dk的方法.

方法1 构造如下的搜索方向dk，

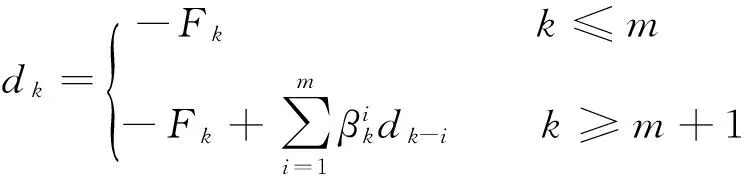
(24)

其中，

(25)

其中，m表示算法记忆先前迭代的步数.

上述构造dk的方法是受文献[11]的启发而得到的. 类似于文献[11]中引理1和引理2的证明方法，可推出下列结论：

(26)

和

‖dk‖≤(1+ρ)‖Fk‖ ∀k.

(27)

方法2 构造如下的搜索方向dk，

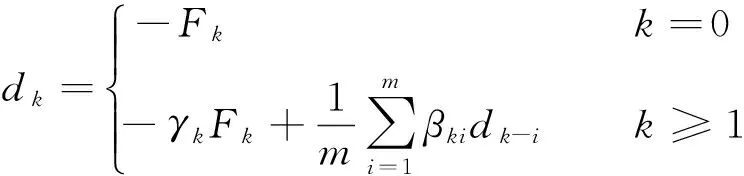
(28)

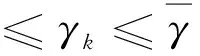
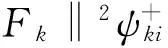
(29)

符号a+由下式定义

而ψki的选取满足关系式

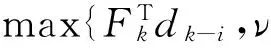
(30)

其中，ν>-1.

上述构造dk的方法是受文献[12]的启发而得到的. 类似文献[12]中引理2.1和引理3.2的证明方法，可推出下列结论：存在常数ω1>0和ω2>0，使得

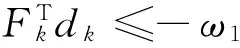
(31)

和

‖dk‖≤ω2‖Fk‖ ∀k ,

(32)

特别地，若映射F：Rn→Rn满足下列单调性假设，则可构造另外2种搜索方向dk.

假设3 映射F满足

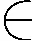
注4 若映射F：Rn→Rn是单调的，则满足特性(2)，但逆命题一般不成立，详见文献[13].

方法3 构造如下的搜索方向dk，

dk=-θkFk,

(33)

其中，

其中，sk-1=xk-xk-1,yk-1=Fk-Fk-1+τsk-1(τ>0).

上述构造dk的方法同文献[2],利用单调性及假设1，可推出下列结论

(35)

和

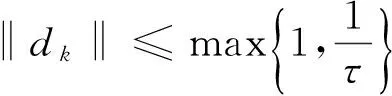
(36)

方法4 构造如下的搜索方向dk，

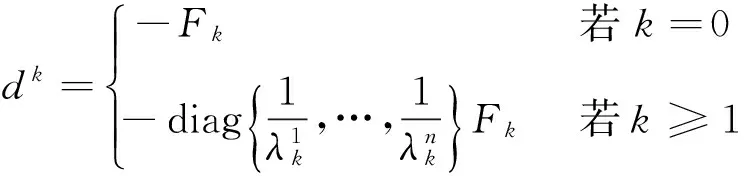
(37)

其中，对i=1,2,…n,

(38)

(39)

而sk-1及yk-1的定义同方法3.

上述构造dk的方法同文献[3],利用单调性及假设1，可推出下列结论

(40)

和

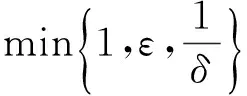
(41)

利用递推式(24)或(28)或(33)或(37)来构造搜索方向dk，并分别用其来代替DFPA算法在Step 2中所构造的dk，而其他步骤不变. 记此时所得到的相应算法分别记为SMA，NSMA，SPA和MSPA. 对4种算法，类似于定理1和2的证明，可推出下列结论.

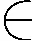
注5 当v=0时，SPA算法和SMPA算法分别同文献[2]和[3]中的算法，但是，文献[2]和文献[3]并未从理论上讨论算法的收敛速度，因此本文定理4的结论解决了该问题.

[1] Sun M, Liu J. Three derivative-free projection methods for nonlinearequations with convex constraints[J]. Journal of Applied Mathematics and Computing, 2015, 47: 265-276.

[2] Yu Z S, Lin J, Sun J, et al. Spectral gradient projection method for monotone nonlinear equations with convex constrains[J]. Applied Numerical Mathematics, 2009, 59: 2 416-2 423.

[3] Yu G H, Niu S Z, Ma J H. Multivariate spectral gradient projection method for nonlinear monotone equations with convex constraints[J]. Journal of Industrial and Management Optimization, 2013, 9: 117-129.

[4] Yamashima N, Fukushima M. On the rate of convergence of the Levenberg-Marquardt method[J]. Computing(Suppl), 2001, 15:237-249.

[5] Fan J Y. On the Levenberg-Marquardt methods for convex constrained nonlinear equations[J]. Journal of Industrial and Management Optimization, 2013, 9: 227-241.

[6] Li D H, Fukushima M, Qi L Q. Regularized Mewton methods for convex minimization problems with singular solutions[J]. Computational Optimization and Applications, 2004, 28: 131-147.

[7] Ma C, Wang C Y. A nonsmooth Levenberg-Marquardt method for solving semi-infinite programming problems[J]. Journal of Computational and Applied Mathematics, 2009,230: 633-642.

[8] Ling C, Wang C F, He H J. A new Levenberg-Marquardt type algorithm for solving nonsmooth constrained equations[J]. Applied Mathematics and Computation, 2014, 229: 107-122.

[9] Yu H D, Pu D G. Smoothing Levenberg-Marquardt method for general nonlinear complementarity problems under local error bound[J]. Applied Mathematical Modelling,2011,35(3):1 337-1 348.

[10] Zhang H C, Hager W W. A nonmonotone line search technique and its application to unconstrained optimization[J].SIAM Journal on Optimization, 2004, 14: 1 043-1 056.

[11] 刘元文, 欧宜贵, 马巍. 一个基于定步长技术的超记忆梯度法[J]. 应用数学, 2014, 28(1): 74-82.

[12] Narushina Y. A nonmonotone memory gradicut method for unconstrained optimization[J]. Journal of the Operations Research Society of Japan，2007，50:31-45.

[13] Solodov M V, Svaiter B F.A new projection method for variational inequality problems[J]. SIAM Journal on Control and Optimization, 1999, 37: 765-776.

Convergence Rate of A Derivative-free Projection Method for Nonlinear Equations

Li Jingya, Ou Yigui

(College of Information Science and Technology, Hainan University, Haikou 570228, China)

In the report, under the local error bound condition, the convergence rate of the derivative-free projection method for a class of nonlinear equations was analyzed, and the sequence {dist(xk,X*)} Q-linearly converges to 0 was proved. So, the whole sequence {xk} R-linearly converges to x*. Moreover, the four general methods are discussed, and their convergence rates are obtained.

nonlinear equations; derivative-free method; projection method; convergence rate

2016-05-31

国家自然科学基金(11261015)；海南省自然科学基金(111001， 20167246)

李靖雅(1993-)，女，甘肃陇南人，海南大学2015级硕士研究生，研究方向：最优化方法，E-mail:373965516@qq.com

欧宜贵(1965-)，男，湖北钟祥人，博士，教授，研究方向：最优化方法，E-mail:ouyigui@126.com

1004-1729(2016)04-0324-06

O 221.2

A DOl：10.15886/j.cnki.hdxbzkb.2016.0049