一类紧支撑正交双向矩阵值小波的构造

库福立，吕 军，阿布力米提·孜克力亚

（新疆农业大学 数学理学院，新疆 乌鲁木齐 830052）

一类紧支撑正交双向矩阵值小波的构造

库福立，吕 军*，阿布力米提·孜克力亚

（新疆农业大学 数学理学院，新疆 乌鲁木齐 830052）

文章引入了双向矩阵值多尺度分辨分析和正交矩阵值小波，得到了双向矩阵值小波存在性的充要条件，给出了双向矩阵值小波的构造算法。

矩阵值小波；正交尺度函数；正交矩阵值小波；两尺度方程

在小波的构造理论中，两尺度加细方程有着重要的作用，杨守志教授在文献［1-2］中，提出了双向加细方程的概念，并引入了双向正交尺度函数和小波函数理论。与传统意义上小波比较，双向小波是一般情形下的小波。向量值小波和矩阵值小波都是一类广义的多小波，但它们与多小波又有区别，比如：实施离散的多小波变换前要滤波，但实施离散的向量值和矩阵值小波变换则不要预滤波。Xia.X.G和B.W.Suter在文献［3］中首先引入正交的向量值小波的概念，给出向量值正交小波的构造方法。自Bacchelli.s在文献［4］给出矩阵值小波理论之后，矩阵值小波理论蓬勃发展，但是目前研究双向矩阵值小波的构造文献较少，文章研究一类双向矩阵值小波的构造理论。

引入记号：R表示实数集，C表示复数集，Z表示整数集，Z+={n:n≥0,n∈Z}.文章n≥2，且n∈Z.In表示n阶单位矩阵，Οn表示n阶零矩阵。

设

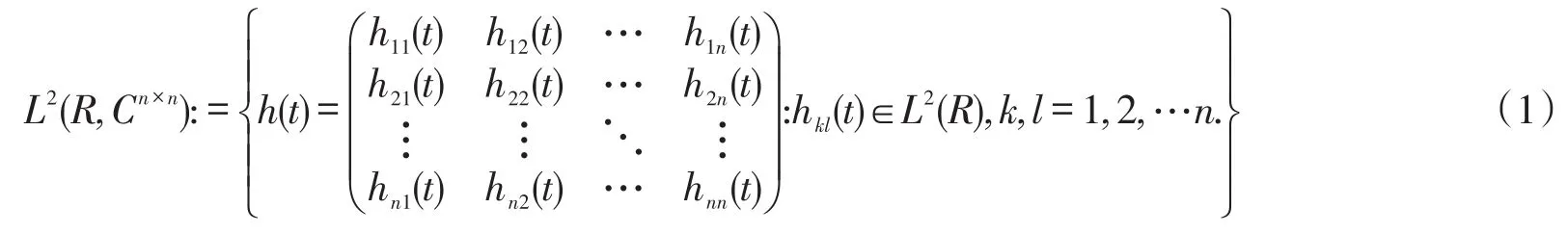
定义矩阵值函数h ( t) ∈L2( R , Cn×n)的范数

定义矩阵值函数h ( t) ∈L2( R , Cn×n)的积分：

定义阵值函数h ( t) ∈L2( R , Cn×n) 的F o u r i e r变换：

定义阵值函数h ( t ) , r ( t) ∈L2( R , Cn×n)的符号内积：

其中∗表示复共轭转置。

1 双向矩阵值多分辨分析

如果紧支撑的矩阵值函数Φ(t)∈L2(R,Cn×n)，满足如下的双向加细方程：

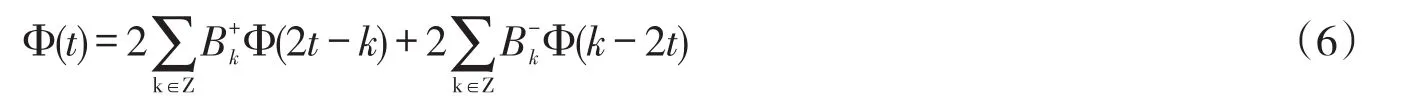
则称Φ(t)双向矩阵值尺度加细函数。

对（6）两边取Fourier变换得：

定义1 定义矩阵值子空间序列Vj⊂L2(R,Cn×n)如下，

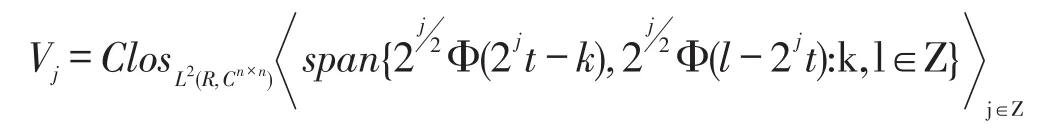
如果对于（2）式定义的{} Vjj∈Z，满足以下条件：

（v）矩阵值函数系列{Φ(t-k),Φ(l-t):k,l∈Z}构成子空间V0的一组Riesz基，则称（6）式定义的矩阵值函数Φ(t)生成了L2(R,Cn×n)中双向矩阵值多分辨分析.

2 双向正交的矩阵值小波

定义2 若双向矩阵值加细函数Φ(t)⊂L2(R,Cn×n)，满足：

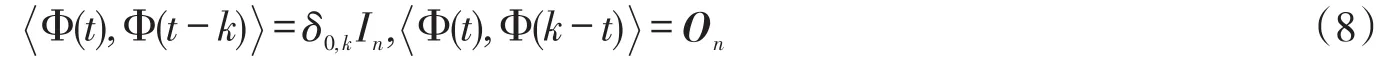
则称Φ(t)是正交的双向矩阵值加细函数，其中k∈Z.

设Wj,j∈Z是Vj在Vj+1中的直交补空间，存在矩阵函数ψ(t)∈L2(R,Cn×n)，构成Wj的一组Riesz基，即

特别的{ψ(t-k),ψ(l-t):k,l∈Z}∈W0⊂V1.若存在n×n紧支撑常数矩阵序列满足：

对（9）式两边取Fourier变换

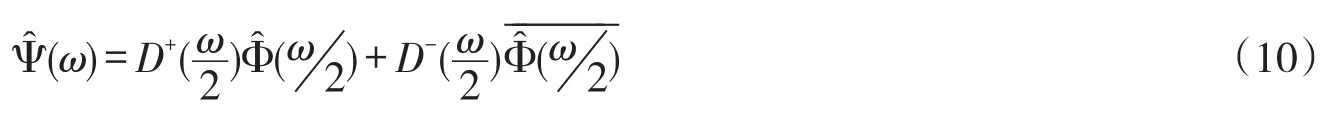
定义3 若Φ(t)⊂L2(R,Cn×n)是双向正交的矩阵值尺度函数，由（9）式给出的双向矩阵值小波函数Ψ(t)，如果Ψ(t)满足：

则称Ψ(t)是正交的矩阵值小波函数，其中k∈Z。

3 双向正交矩阵值小波的存在性

定理3.1 若Φ(t)⊂L2(R,Cn×n)是双向正交矩阵值尺度函数，并且Φ(t)由（6）式所定义，则对于∀k∈Z，有

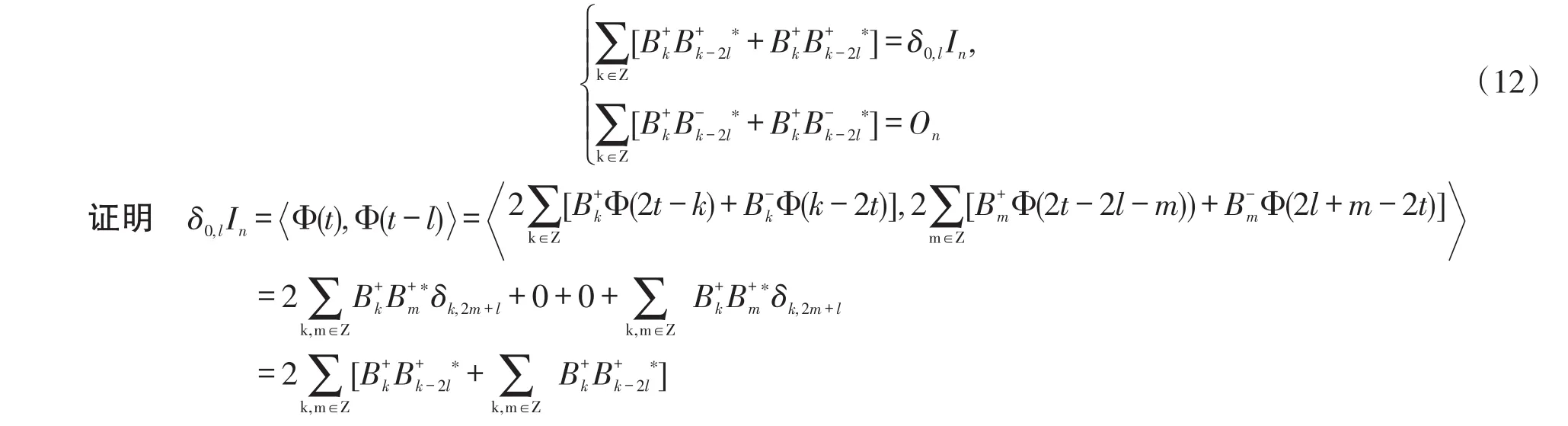
对于第2个式子，同理可证。

定理3.2 若Φ(t)是双向矩阵值尺度函数，ψ(t)是对应的小波函数，分别是与之对应的正向面具符号、负向面具符号，则∀j∈Z满足：

证明类似定理3.1的证明。

4 双向正交矩阵值小波的构造

定理4.1 若Φ(t)紧支撑的双向正交矩阵值尺度函数，κ是某个正整数且满足κ>3，记éκù=inf{n:n≥x,n∈Z}，并且有如下的方程：

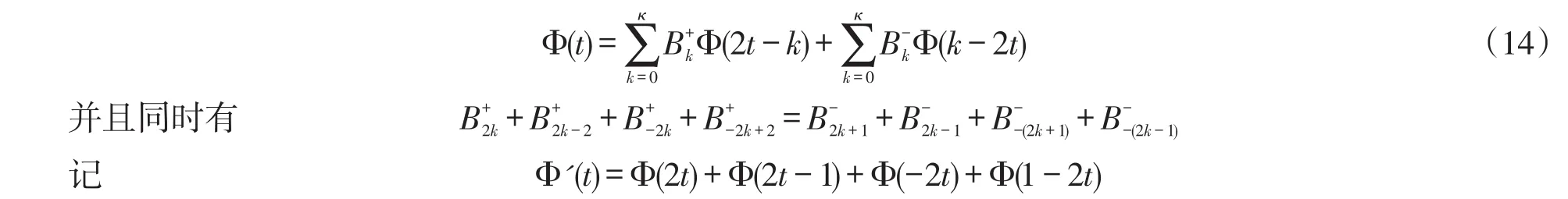
则有：（i）Φ'(t)是紧支撑双向正交矩阵值尺度函数；

证明：类似文献［6］定理2的证明。

此定理说明支撑区间为[0,κ]的双向矩阵值尺度函数可转化为支撑区间为的矩阵值尺度函数，为了研究方便，仅讨论双向加细方程的系数矩阵,其余的皆为零矩阵的构造算法。

定理4.2 设Φ(t)⊂L2(R,Cn×n)是紧支撑的正交的双向矩阵值尺度函数，满足如下方程：

如果有某个正整数s,0≤s≤3，使得Hermite矩阵Qr满足：

再定义：

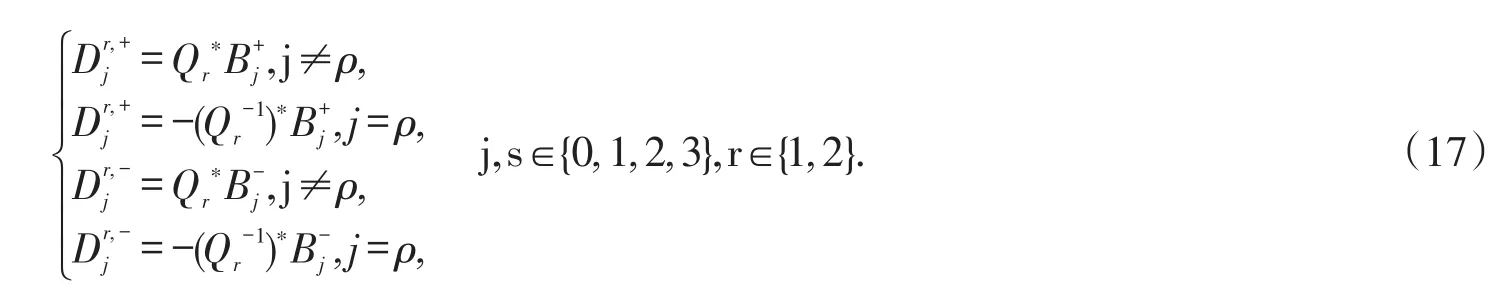
则可以得到，与Φ(t)尺度函数对应的双向正交矩阵值小波函数

证明与定理4.1类似。

［1］杨守志，李尤发.具有高逼近阶和正则性的双向加细函数和双向小波［J］.中国科学A辑：数学，2007，37（7）：770-795.

［2］Yang SZ.Biorthogonal two-direction refinable function and two-direction w-avelet［J］.Applied Mathematics and Computation，2006，182（2）：1717-1724.

［3］X.G.Xia，B.W.Suter.Vector-valued waveletsand vector filterbanks［J］.IEEETransactions Signal Processing，1996，44（3）：508-518.

［4］Yang SZ，Cheng ZX，Wang H Y.Construction ofbiorthogonalmultiwavelets［J］.Mathematicalanalysisand Applications，2002，276：1-12.

［5］Chen Q J，Cheng Z X，Wang C L.Existence and construction of compactly supported biorthogonalmultiple vector-valued wavelets［J］.Journal of Applied Mathematicsand Computing，2006，22（3）：101-115.

［6］Chen Q J，Cheng Z.A study on compactly supported orthogonalvector-valued waveletsand waveletpackets［J］.Chaos，Solitons&Fractals，2007，31 （4）：1024-1034.

［7］Chen Q J，Shi Z.Biorthogonalmultiple vector-valuedmultivariatewavelet pac-ketsassociated with a dilationmatrix［J］.Chaos，Solitons&Fractals，2008，35（2）：323-332.

［8］陈清江，王满.矩阵伸缩的多元多重向量值小波包的双正交性［J］.高等学校计算数学学报，2009，31（3）：267-276.

［9］Chen Q J，Qu XG.Characteristicsofa class of vector-valued non-separable higher-dimensionalwaveletpacketbases［J］.Chaos，Solitons&Fractals，2009，41（4）：1676-1683.

［10］Lisuo Luo，Wanshe Li，Qiao Li.A study on orthogonal two-direction vector vallued waveletsand two-directionwavelet packets［J］.Applied Mathematicsand Computation.2011，21（7）：10146-10157.

Construction of Com pactly Supported Orthogonal Tw o-d irection M atrix-valued W avelet

KU Fu-li，LV Jun，ABLIMIT·Zikerya

（SchoolofMathematicsXinjiang AgriculturalUniversity，Urmuqi，Xinjiang，830052，China）

The concept two-direction Matrix-values function and two-direction Matrix-valueswavelet is generalized to the orthogonal，the necessary and sufficient conditions for two-waymatrixwaveletexistence，illustrating how tousemethod to constructaorthogonal two-direction Matrix-valueswavelets.

Matrix-valued wavelet;Orthogonal scale function;Biorthogonalmulti-wavelet;Two-scalematrix equation

O174.21

A

1008-9659（2016）04-0031-04

2016-06-30

新疆农业大学校前期资助课题（XJAU201524）。

库福立（1986-），男，湖北麻城人，助教，主要从事小波分析及其应用方向的研究。

*［通讯作者］吕 军（1988-），男，湖北鄂州人，讲师，主要从事小波分析及其应用方向的研究。