基于有限元法和解析法的肋骨冷弯机机架结构分析

吕 骁， 陈 强， 刘 鹏， 马 浩， 邵伟伟

(上海船舶工艺研究所， 上海 200032)

基于有限元法和解析法的肋骨冷弯机机架结构分析

吕 骁， 陈 强， 刘 鹏， 马 浩， 邵伟伟

(上海船舶工艺研究所， 上海 200032)

肋骨冷弯机机架是整台设备的“骨架”，往往承受着巨大的夹紧力和主弯曲油缸力，其可靠性与整机的可靠性密不可分，其中机架的强度是考核其可靠性的首要指标。基于解析法和有限元法分别对400 t级肋骨冷弯机的中、边机架进行强度分析，结果表明两种方法的结果高度吻合、误差较小，各机架的危险部位(薄弱环节)位于其上端的过渡圆角处，在规定的安全系数下，最大应力小于许用应力，强度能够满足使用要求。

肋骨冷弯机机架；解析法；有限元法；强度

0 前言

船舶肋骨冷弯是船体建造过程中的关键工序之一，肋骨冷弯过程属于型材(大部分是型钢)的塑性变形。目前国内外专家学者[1-4]已对其成形机理进行了大量的理论及实验研究，并取得了丰硕的成果。

基于型材塑性成形领域的研究成果，上海船舶工艺研究所经过数十年的潜心研究，于20世纪90年代初成功研制出国内外第一台50 t级肋骨冷弯机，解决了多项关键技术问题，首创了弦线测量法的在线监测控制方式与逐步逼近法的成形工艺方式，前者用于保证型材的实际弯制线形与理论线形相吻合，而后者则用于解决型材弯制过程中产生的回弹问题。经过不断地升级换代、技术改进，上海船舶工艺研究所的肋骨冷弯机实现了高度智能化、集成化，至今已形成了50 t，100 t，160 t，250 t，400 t等系列的产品，广泛应用于角钢、T型钢、扁钢和球扁钢的弯制，能够满足目前船体建造的需求。

目前肋骨冷弯的自动化加工原理分为三支点弯曲原理和四支点纯弯曲原理。尽管四支点纯弯曲原理具有加工质量好、加工效率高等优点，但由于其在支点具有较大的应力集中，且存在设备结构复杂等缺陷，因此当前肋骨冷弯机仍普遍采用三支点弯曲工作原理，型材分别由中机架和两个边机架的夹紧机构负责夹紧。其中，中机架作为三支点中的中间支点，而边机架作为三支点中的两端支点，它们均由冷弯机的底座支撑。中机架上搭载着主弯曲油缸、夹紧油缸、检测机构、中上模具、中下模具、前模具和后模具等部件。工作时，由主油缸推动中机架在底座上前后移动完成肋骨的弯制，肋骨的形状由4个模具保证，故而中机架是肋骨塑性成形的主要作业区域，也是肋骨成形精度的检验测量区域。边机架上搭载着夹紧油缸和能够跟肋骨随动的上、下模具，根据型材的规格不同，弯制时其支点距离也不尽相同。本机的边机架可以根据实际需要通过手动方式来使边机架相互靠近或分开，能够满足不同支点距离的要求。综上所述，机架作为整台设备的“骨架”，其应具有足够的强度。

随着有限单元法的日益成熟，目前已被广泛应用于机械、化工、材料和物理研究等领域，为机械结构的创新设计及强度、刚度的校核提供了新的手段。一些学者[5-6]以ANSYS软件为工具，分析了轧机机架的应力分布和变形情况，结果表明最大应力出现在压下螺母孔圆角处。李霞等[7]基于ANSYS软件对番茄翻秧机机架进行了有限元分析，获得了机架的变形特征及应力分布情况。在不同工况下，翻秧机的最大应力均出现在机架顶端连接处，而最大位移则位于横梁的末端，并根据沿横梁的应力分布情况，提出了结构的改进方向。宗荣珍等[8]则针对带式输送机的机架进行了结构分析，确定了机架在载荷作用下的最大应力值及变形值。肖成林等[9]在CATIA软件中建立了耕整机的参数化模型，分析了耕整机的工况，并采用ANSYS软件对机架进行了强度和刚度分析，得到了机架的应力分布情况。针对万能型钢轧机，宋剑锋等[10]应用ANSYS软件对其机架圆角进行多目标优化设计，使机架在满足强度条件的前提下，在质量较小的时候得到较大的刚度。顾忠新等[11]基于ANSYS软件分析了折弯机机架的动态、静态性能，计算结果与工程实测值基本吻合。

本文从数控肋骨冷弯机的机架出发，以满足技术指标为条件，分别采用理论计算和有限元仿真计算手段，从强度层面对机架进行评价，将理论计算结果与有限元仿真计算结果进行了对比、分析与讨论，两者结果相互印证。

1 机架的有限元计算

有限元方法的应用有效地解决了大型复杂构件的应力难以计算、强度难以校核、传统理论计算需要简化的细节较多、计算精度较低、与实际使用结果相差较大等难题。运用化整为零的思想，将大型的、复杂的和理论难以计算的零件、部件甚至整机进行离散化，每个单元作为一个单独的计算域分别计算，最后在相邻单元的边界依据协调方程将所有单元的计算结果统一就能够得到精度较高的计算结果。

本文选用的400 t级肋骨冷弯机，主油缸最大推力为4 000 kN，根据以往的设计及现场经验，在采用最大推力进行型材弯制时，为了保证型材不发生窜动，中机架需提供的最大夹紧力一般为主油缸最大推力的1/4即1 000 kN，而边机架提供的最大夹紧力为中机架的一半即500 kN。

1.1 中机架有限元分析

1.1.1 机架实体模型简化

首先在Solidedge三维设计软件中建立肋骨冷弯机中机架的三维模型，由于原模型中存在众多结构细节，若全部保留这些细节不仅会增加有限元网格的划分难度，而且会使得计算时间大幅提高，甚至可能由于计算机性能的限制而造成计算失败。因此，为了提高效率，降低计算机的资源占用，必须对原模型进行合理简化。简化过程需满足等效性原则，即简化后的模型能够如实反映机架的主要力学特性。这样可以去除螺栓孔、小倒角和工艺孔这些为了满足加工、装配要求但属于非主要受力的结构。简化后的模型如图1所示。

图1 中机架简化实体模型

1.1.2 网格划分

将三维模型传递到有限元软件中，由于简化后的模型形状比较规整，考虑使用六面体实体单元进行网格划分，能够适当提高计算效率及结果精度。网格划分完成后，形成了中机架的有限元模型，如图2所示，其中模型节点总数143 353，单元总数36 322。机架结构材料为Q235，其材料特性如表1所示。

图2 中机架有限元模型

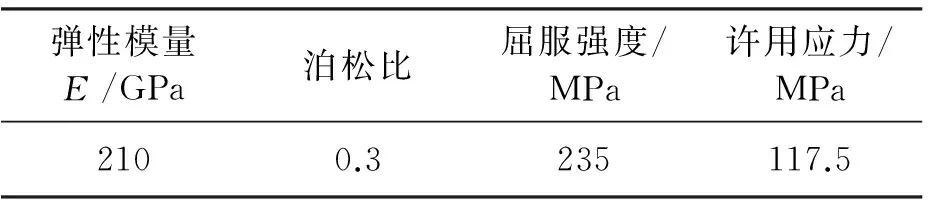
弹性模量E/GPa泊松比屈服强度/MPa许用应力/MPa2100.3235117.5

1.1.3 载荷及约束施加

结合实际工况的弯制工艺参数，在中机架有限元模型的受力面上施加均布面载荷，根据前文所述，总载荷力为1 000 kN，在机架底部施加固定约束，如图3所示。

图3 中机架载荷及约束

1.2 边机架有限元分析

同理，边机架也采用相同步骤进行处理，边机架简化模型如图4所示。同样对边机架进行有限元网格划分(如图5所示)、划分完共有117 696个节点，31 268个单元。在边机架有限元模型的受力面上施加均布面载荷500 kN，底面施加固定约束，如图6所示。

图4 边机架简化实体模型

图5 边机架有限元模型

图6 边机架载荷及约束

1.3 计算结果

经过求解输出Von Mises等效应力，中机架、边机架的应力云图分别如图7和图8所示。

由图7和图8可知：中机架危险截面位于机架上部的过渡圆角处，危险截面的应力为57 MPa；边机架危险截面位于机架上部的过渡圆角处，危险截面的应力为30.6 MPa。

2 机架分析解析法介绍

2.1 中机架结构的解析计算

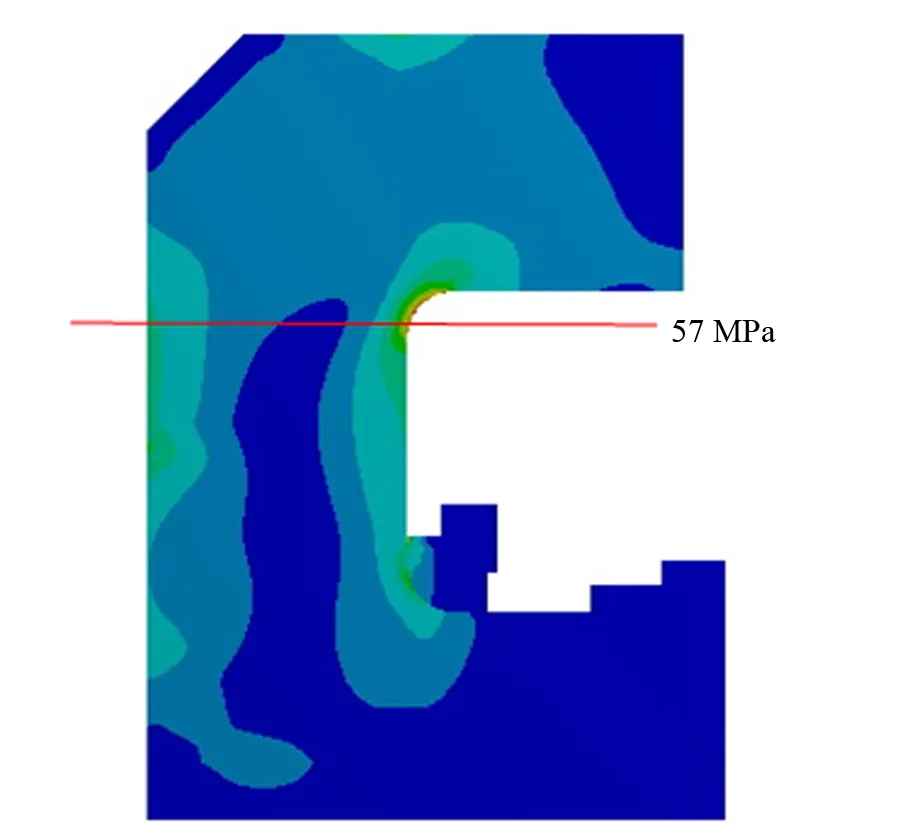
图7 中机架应力分布云图

中机架结构的主要尺寸及工作载荷示意图如图9所示。

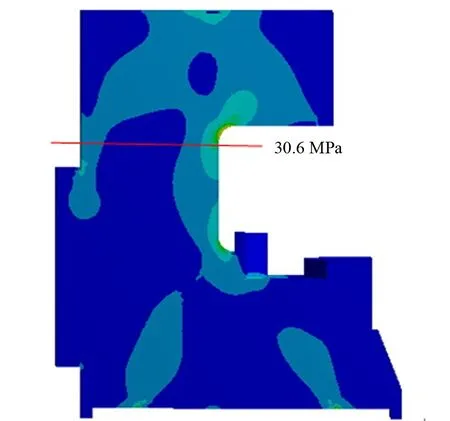
图8 边机架应力云图

图9 中机架主要尺寸示意图

首先确定A-A为危险截面，根据材料力学上的相关理论，确定危险截面上Z轴的形心位置Z0。

因此Y轴的主惯性矩Iy0为

又由于A-A截面面积A为

A = 2 ×0.657 m×0.06 m+ 0.057 m×0.38 m

= 0.100 5 m2

且夹紧力：N0=1 000×103N。

因此弯矩：My0=N0· L = (1 000×103) N×(0.47 m+0.264 m)=734×103N·m。

A-A截面上的正应力σ正0为

=9.95×106N/m2=9.95 MPa

A-A截面上弯曲应力σy0为

=44×106N/m2=44 MPa

最终可求得危险截面A-A上的最大应力σ总0为

σ总0=σ正0+σy0=9.95 MPa+44 MPa

=53.95 MPa。

2.2 边机架结构的解析计算

边机架的主要尺寸及工作载荷示意图如图10所示。

图10 边机架主要尺寸示意图

首先确定B-B为危险截面，根据材料力学上的相关理论，确定危险截面上Z轴的形心位置Z1为

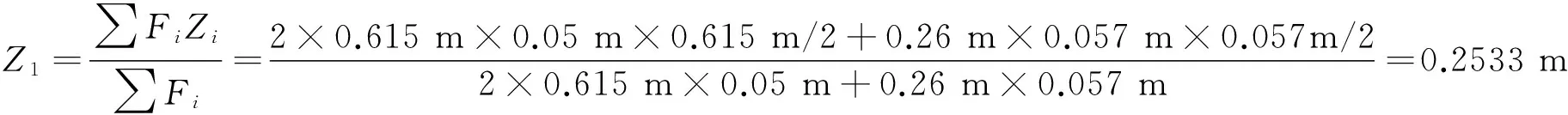
因此Y轴的主惯性矩Iy1为

又由于B-B截面面积B为

B= 2 ×0.615 m×0.05 m+ 0.26 m×0.57 m

= 0.076 32 m2

且轴向力：N1=500×103N。

弯矩：My1=N· L = (500×103) N×(0.3 m+0.253 3 m)=276.65×103N·m。

因此B-B截面上的正应力σ正1：

=6.55 MPa

B-B截面上弯曲应力σy1为

=24.2×106N/m2=24.2 MPa

最大应力σ总1为

σ总1=σ正1+σy1=6.55 MPa+24.2 MPa

=30.75 MPa。

机架体材料用Q235，其屈服强度σs=235 MPa，取安全系数n=2，则许用应力[σ]= σs/n=117.5 MPa。由上述有限元分析与解析法计算结果可知：σ总0，σ总1<[σ]，因此，中、边机架满足强度要求。

3 结论

通过对工程法和有限元法分别计算得到的结果进行分析，可以得出以下结论。

(1) 两种方法计算得到的计算结果相对误差在10%以内，结果吻合度较高，有较好的一致性。由于工程法对于原始模型简化较多，因此相对于有限元法，其精度还存在着一定的差距。

(2) 有限元法计算结果表明，中、边机架的最大应力处均出现在结构上部的过渡圆角处，最大位移均出现在机架上部的前端，其最大应力和位移均满足设备的强度及刚度要求，因此机架结构的设计是可靠的。

(3) 采用有限元法计算得到的是整个机架的应力云图与位移云图，结果更为直观、准确，且可以查看任意细节的应力和位移状态，对以后机架的结构参数确定和优化设计具有较好的指导意义。传统工程方法简便快捷，能够在设备的初步设计中提供有效指导，将两者兼顾使用，取长补短，在实际设计中既提高设计效率又保证设计精度，充分提升设计水平。

[1] ATELSON K A, KRAMER A. Distortion of U-channel section in plastic bending[J]. ASEM Journal of Manufacturing Science and Engineering, 1999(121)：208-213.

[2] TRAHAIR N S. Moment capacities of steel angle sections[J]. Journal of Structural Engineering, 2002, 128(11): 1387-1393.

[3] TRAHAIR N S. Biaxial bending of steel angle section beams[J]. Journal of Structural Engineering, 2003, 129(6)：784-791.

[4] XU Y, ZHANG L C, YU T X. The elastic-plastic pure bending and spring back of L-shaped beams[J]. International Journal of Mechanical Science, 1987(29): 425-433.

[5] 吴旭春, 李佑河, 黄贞益, 等. 基于ANSYS的型钢轧机机架有限元分析[J]. 冶金设备, 2010(3):38-40.

[6] 唐前辉, 吕立华, 马靳江. 基于ANSYS的轧机机架有限元分析[J]. 重庆科技学院学报, 2008, 10(4): 57-59.

[7] 李霞, 徐为民. 基于ANSYS番茄翻秧机机架的有限元分析[J]. 机械设计与制造, 2010(1): 56-58.

[8] 宗荣珍, 薛党勤, 李文民. 基于ANSYS的带式输送机机架结构分析[J]. 矿山机械, 2008, 36(11): 66-68.

[9] 肖成林, 周德义, 王永强, 等. 基于ANSYS的耕整机机架有限元分析[J]. 吉林农业大学学报, 2011, 33(4): 459-463.

[10] 宋剑锋, 张文志, 董永刚. 基于ANSYS软件的万能型钢轧机机架圆角的多目标优化设计[J]. 重型机械, 2006(2): 40-42.

[11] 顾忠新, 胡智明. 基于ANSYS折弯机机架的有限元分析[J]. 锻压装备与制造技术, 2014(1): 26-28.

Structure Analysis for the Racks of Cold Frame Bender Based on Analytical Method and Finite Element Method

LYU Xiao, CHEN Qiang, LIU Peng, MA Hao, SHAO Weiwei

(Shanghai Shipbuilding Technology Research Institute, Shanghai 200032, China)

The racks of cold frame bender act as the skeleton which are generally subject to enormous clamping force and main bending cylinder force. The strength of racks is the prior index for reliability which is related to the device. The strength of middle and side racks are analyzed based on the analytical method and the finite element method respectively. The results obtained from the two methods are highly consistent with seldom errors,and the damage sites(weak link)are located at the corner of the top of racks. However, the maximum stress is lower than permissible stress at the specified safe factor, and the strength meets the acquirement.

rack of cold frame bender; analytical method; finite element method; strength

吕 骁(1986-)，男，硕士，主要从事机械设计方面的研究。

TH114

A