基于去均值归一化互相关方法的复合材料板低速冲击定位*

陆 观，徐一鸣，邱自学，梁大开

（1.南通大学机械工程学院，江苏南通226019；2.南通大学电气工程学院，江苏南通226019；3.南京航空航天大学机械结构力学与控制国家重点实验室，南京210016）

基于去均值归一化互相关方法的复合材料板低速冲击定位*

陆 观1，徐一鸣2*，邱自学1，梁大开3

（1.南通大学机械工程学院，江苏南通226019；2.南通大学电气工程学院，江苏南通226019；3.南京航空航天大学机械结构力学与控制国家重点实验室，南京210016）

为了实现无需先验知识的复合材料结构低速冲击定位，提出了一种基于去均值归一化互相关的冲击定位方法。采用归一化互相关方法，首先对所有冲击样本信号和待定信号进行去均值归一化，然后计算样本信号和待定信号的综合互相关值，最后确定定位参考区域，通过样本信号与待定信号间的互相关结果来评估冲击位置。实验结果表明该方法可以准确评估复合材料板低速冲击位置，其中最大误差为34.76 mm，平均误差为11.07 mm。

光纤布拉格光栅；冲击定位；去均值归一化互相关；复合材料板

近年来，复合材料凭借高比强、高比刚等优异力学性能，在各领域结构中的使用已显著增加。然而，复合材料受到外部低速冲击时易造成内部裂纹或分层。这些隐藏在复合材料结构中的损伤会导致结构机械性能极大退化，甚至会导致整个结构的灾难性故障［1-2］。为了检测复合材料结构各种形式的内在损伤，研究人员采用了多种无损检测方法，包括电涡流、超声波、射线、热成像、Lamb波等［3-5］。然而，无损检测方法在中止整体结构运行进行检查时，需要耗费过度的时间和成本，大大降低了此方法对于大型结构的可操作性。因此，可以通过实时监测结构可能受到的外部冲击，有效评估冲击位置并减少整个无损检测的时间和成本［6］。

为了识别结构的外部低速冲击，可以安装多种传感器进行监测，并对测量到的冲击信号采用定位算法进行后处理。已有的冲击定位方法大多数需要先验知识，如群速度或目标结构的几何构造［7-9］。为了克服传统冲击定位方法的这些缺点，Park J等［10］利用传感器位置和冲击位置对传递函数，通过最小化代价函数识别了复合材料板上的冲击；Haywood J等［11］利用传感器信号特征及神经网络，确定了复合材料板的冲击位置；Jang B W等［12］通过比较参考信号数据库和新获取冲击信号之间的均方根值，对复合材料加筋板进行了冲击定位；Hiche C等［13］研究了一种基于应变幅度的定位算法，通过比较光纤光栅传感器测量到的冲击信号的最大应变幅度绝对值来定位冲击源。目前相关研究通过使用一些无需先验知识的定位方法成功识别了结构冲击位置，但是较少涉及光纤传感技术。

由于重量轻、体积小、耐腐蚀、可嵌入性、方便复用、无电磁干扰效应等优良特性［14］，光纤光栅传感器适用于复合材料结构无损检测［15-16］。因此，针对复合材料结构冲击信号分析和先验知识获取的复杂情况，本文利用光纤布拉格光栅传感网络，通过针对冲击信号的去均值归一化互相关方法，进行了复合材料板冲击定位研究。

1 冲击定位算法

1.1 去均值归一化互相关算法

归一化互相关算法是一种信号处理方法，用于表示两种不同信号间的相似性。当两个信号的波形和相位相似时，互相关值较高。本文提出的冲击信号去均值归一化互相关算法分为两步：冲击响应信号去均值、信号归一化互相关运算。

冲击响应信号去均值即把信号向量x的均值xˉ变为0，去均值后的信号向量为x′。由于不同温度、相同位置、相同能量下的冲击信号均值不同，但信号波形、时域幅值相似，因此去均值化步骤可以去除温度因素对传感器中心波长的交叉干扰。

信号x和y间去均值互相关定义为：

式中，*代表去均值互相关运算，t是信号的时间参数，τ是两信号间的时滞。

为了统一信号基准，对去均值冲击信号需要进行基准转换，即通过自身冲击信号进行归一化运算。则两信号间的去均值归一化互相关表示为：

式中，信号x的去均值归一化常数X是信号时域总能量的平方根，表示为：

同理，信号y的去均值归一化常数可以表示为：

如果两个冲击信号代表相同位置不同能量的冲击状态，则信号波形相似但信号时域幅值不同。在理想的情况下，两个冲击信号间的关系可以表示为：

式中，n为常数。

将式（5）代入式（2）得到两信号间的去均值归一化互相关运算为：

其中，当τ为0时，式（6）有最大值1。

以上推导过程表明利用去均值归一化互相关算法，可以有效提取基于冲击位置的信号特征。冲击信号特征可用于评估冲击载荷的实际位置。

1.2 冲击定位算法步骤

在冲击定位过程中，通过样本信号与待定信号间的互相关结果来评估冲击位置。首先，需要对所有冲击样本信号和待定信号进行去均值归一化；然后，计算样本信号和待定信号的综合互相关值，即传感器网络中计算得到的信号互相关值总和；最后，由于位于实际冲击点附近的样本点会表现出较高的互相关值，因此选择拥有前5%最大互相关值的样本点组成定位参考区域，用于评估实际冲击位置。综上，针对复合材料层合板的冲击定位算法具体步骤如下：

①在L个冲击位置采集数据，每个位置由N个传感器采集到的冲击响应信号向量组成了信号矩阵mi=(xi1,xi2,…,xiN)（其中i=1,2,3,…,L），作为冲击样本信号。

②对信号矩阵进行去均值归一化，得到去均值后的冲击样本信号为mi′=(xi1′,xi2′,…,xiN′)（其中，i=1,2,3,…,L，j=1,2,3,…,N），其去均值归一化向量Mi′=(Xi1′,Xi2′,…,XiN′)由以下归一化常数组成：

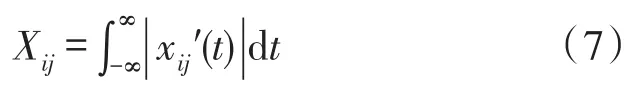
③同理，将采集的待定位冲击信号d=(y1,y2,…,yN)去均值归一化，得到d′=(y1′,y2′,…,yN′)及去均值归一化常数：

④针对冲击样本信号与待定位冲击信号进行去均值归一化互相关运算，分别计算信号d与L个冲击样本信号mi间的综合互相关值为：

⑤比较γ1、γ2、…γL数值大小，取最大值的前5%为冲击定位参考区域边界点。计算参考区域质心，作为判定的冲击位置。

2 冲击实验与结果分析

2.1 冲击实验系统

复合材料板的冲击实验系统由碳纤维层合板试件、冲击锤、光纤布拉格光栅传感器、光纤光栅SI425型解调仪以及计算机组成，如图1所示。其中复合材料板试件四边固支，材料为T300/QY8911，尺寸为600 mm×600 mm，钢质固支架边框宽度为30 mm，底面粘贴了4个栅长为10 mm的光纤布拉格光栅传感器，传感器排布如图2所示，传感器位置与光纤光栅中心波长值见表1。冲击实验有效区域大小为540 mm×540 mm，划分的网格大小为45 mm×45 mm。手持式冲击锤能量可调，可对板试件任意位置进行冲击。

图1 冲击实验系统

表1 传感器波长与位置

图2 光纤光栅传感器排布图

冲击实验系统利用光纤布拉格光栅监测冲击信号，冲击锤在板试件上产生冲击信号，光纤布拉格光栅传感器中心波长值随之发生偏移，偏移值组成的冲击响应信号由光纤光栅解调仪实时监测并传输到计算机，解调仪同时连接4个传感器。

2.2 建立冲击样本信号库

复合材料板的冲击样本信号库通过所有样本点的冲击样本信号来建立。为了建立用于冲击定位的样本信号库，使用冲击锤分别对冲击实验区域的121个网格线交叉点进行冲击，如图1中所示。每个样本信号采用250 Hz采样率采集500 ms，即采样次数为125次。图3和图4为4个FBG传感器采集的冲击样本信号示例，以点（270 mm，270 mm）、（415 mm，360 mm）为例，其中各点样本信号的波形和幅值特征变化都与冲击位置变化相对应。采用的冲击定位方法通过直接对比冲击信号特征识别结构冲击位置。

图3 复合材料板（270 mm 270 mm）传感网络信号

2.3 冲击定位分析

为了检验定位方法的性能，在复合材料板上选择了15个冲击点进行验证实验，研究了冲击信号归一化对于定位性能的影响。通过定位误差评估该方法定位性能，定位误差由实际冲击位置和预测冲击位置间的绝对距离计算得出。

图4 复合材料板（415 mm 360 mm）传感网络信号

如图5为15个验证点的冲击定位结果，冲击定位算法一为去均值归一化互相关定位方法，算法二为一般互相关定位方法。其中当采用一般互相关定位方法时，点1和点13的定位误差大于网格尺寸（45 mm）。图5显示了两种冲击定位方法对比结果，其中去均值归一化互相关方法显然比一般互相关定位方法的性能更好。

图5 复合材料板定位验证实验结果

由于去均值归一化步骤能够减少冲击能量改变的影响并使定位参考区域相对集中，因此可以提高定位精度。另外，由于传感器光纤轴和冲击信号波传播方向夹角影响了检测灵敏度，当冲击发生在光纤轴和冲击位置夹角较大的区域时，冲击信号幅值会大大减少，这也导致了误差的增大。综上所述，去均值归一化互相关定位方法能够更准确地评估冲击位置，实验证明此方法可成功进行冲击定位，其中最大误差为34.76 mm，平均误差为11.07 mm。定位结果符合工程应用范围，其中定位平均误差由31.47 mm显著减少到11.07 mm。

3 结论

①针对复合材料结构冲击信号特性，提出了基于去均值归一化互相关的冲击定位方法。采用无需先验知识的去均值归一化互相关运算，通过对比冲击信号特征进行定位，并给出了复合材料结构冲击定位步骤。

②搭建了复合材料板低速冲击定位系统，通过实验验证了提出的冲击定位方法的性能。实验证明，该方法可以准确评估冲击位置，其中最大误差为34.76 mm，平均误差为11.07 mm，定位结果符合工程应用范围。去均值归一化步骤（尤其在冲击幅值较小时）显著提升了定位性能，其中定位平均误差由31.47 mm显著减少到11.07 mm。

［1］Ciampa F，Meo M.A New Algorithm for Acoustic Emission Localization and Flexural Group Velocity Determination in Anisotropic Structures［J］.Composites Part A：Applied Science and Manufacturing，2010，41（12）：1777-1786.

［2］Tserpes K I，Karachalios V，Giannopoulos I，et al.Strain and Damage Monitoring in CFRP Fuselage Panels Using Fiber Bragg Grating Sensors.Part I：Design，Manufacturing and Impact Testing［J］.Composite Structures，2014，107：726-736.

［3］Diamanti K，Soutis C.Structural Health Monitoring Techniques for Aircraft Composite Structures［J］.Progress in Aerospace Sciences，2010，46（8）：342-352.

［4］Doyle D，Zagrai A，Arritt B，et al.Damage Detection in Bolted Space Structures［J］.Journal of Intelligent Material Systems and Structures，2010，21（3）：251-264.

［5］Djinovic Z，Scheerer M，Tomic M.Impact Damage Detection of Composite Materials by Fiber Bragg Gratings［J］.Proceedings of SPIE-Smart Sensors，Actuators，And Mems V，2011，8066.

［6］Takeda S，Aoki Y，Nagao Y.Damage Monitoring of CFRP Stiffened Panels under Compressive Load Using FBG Sensors［J］.Composite Structures，2012，94（3）：813-819.

［7］Meo M，Zumpano G，Piggott M，et al.Impact Identification on aSandwich Plate from Wave Propagation Responses［J］.Composite Structures，2005，71（3-4）：302-306.

［8］Yuan S，Zhong Y，Qiu L，et al.Two-Dimensional Near-Field Multiple Signal Classification Algorithm-Based Impact Localization［J］.Journal of Intelligent Material Systems and Structures，2014，26（4）：400-413.

［9］Ruiz M，Mujica L E，Berjaga X，et al.Partial Least Square/Projection to Latent Structures（PLS）Regression to Estimate Impact Localization in Structures［J］.Smart Materials and Structures，2013，22（2）：025028.

［10］Park J，Ha S，Chang F K.Monitoring Impact Events Using a System-Identification Method［J］.Aiaa Journal，2009，47（9）：2011-2021.

［11］Haywood J，Coverley P T，Staszewski W J，et al.An Automatic Impact Monitor for a Composite Panel Employing Smart Sensor Technology［J］.Smart Materials and Structures，2005，14（1）：265-271.

［12］Jang B W，Lee Y G，Kim C G，et al.Impact Source Localization for Composite Structures under External Dynamic Loading Condition［J］.Advanced Composite Materials，2015，24（4）：359-374.

［13］Hiche C，Coelho C K，Chattopadhyay A.A Strain Amplitude-Based Algorithm for Impact Location on Composite Laminates［J］.Journal of Intelligent Material Systems and Structures，2011，22（17）：2061-2067.

［14］孙媛凯，李英娜，胡明耀，等.输电铁塔塔身光纤光栅结构监测与时序融合研究［J］.传感技术学报，2016，29（3）：451-455.

［15］Kirikera G R，Balogun O，Krishnaswamy S.Adaptive Fiber Bragg Grating Sensor Network for Structural Health Monitoring：Applications to Impact Monitoring［J］.Structural Health Monitoring，2011，10（1）：5-16.

［16］常新龙，何相勇，周家丹，等.FBG传感器在复合材料固化监测中的应用［J］.传感技术学报，2010，23（5）：748-752.

陆 观（1983-），女，江苏南通人，博士，南通大学副教授，主要从事先进传感技术及结构健康监测等方面的研究，luguan@ntu.edu.cn；

徐一鸣（1981-），男，江苏南通人，博士，南通大学副教授，主要从事数字图像处理及先进传感器技术等方面的研究，yimingx@ntu.edu.cn。

The Low Velocity Impact Localization Based on Mean-Residual Normalized Cross-Correlation for Composite Plate*

LU Guan1，XU Yiming2*，QIU Zixue1，LIANG Dakai3
（1.School of Mechanical Engineering，Nantong University，Nantong Jiangsu226019，China；2.School of Electrical Engineering，Nantong University，Nantong Jiangsu226019，China；3.State Key Laboratory of Mechanics and Control of Mechanical Structures，
Nanjing University of Aeronautics and Astronautics，Nanjing210016，China）

In order to localize the low velocity impacts（LVI）for composite structure without prior information，an impact localization method based on mean-residual normalized cross-correlation was proposed.The paper adopted normalized cross-correlation method to normalize all impact sample signals and undetermined signals firstly.After that，the complex cross-correlation values were calculated and the localization reference area was determined.Finally，the impact location was estimated by using cross-correlation results between sample signals and undetermined signals.The experimental results show that the proposed method can evaluate the LVI positions for composite plate accurately，the maximal error is 34.76 mm and the standard error is 11.07 mm.

optic-fiberBragggrating；impactlocalization；mean-residualnormalizedcross-correlation；compositeplate

TP212

A

1004-1699（2016）12-1810-05

��7200

10.3969/j.issn.1004-1699.2016.12.005

项目来源：国家自然科学基金项目（61273024，51307089）；交通运输部应用基础研究项目（2014319813180）；江苏省产学研前瞻性联合研究项目（BY2015047-11）；江苏省教育厅面上项目（14KJB510030）；南通大学自然科学研究专项项目（13ZJ003）

2016-05-28修改日期：2016-08-11