碳纤维复合材料卫星杆件优化设计

郑传祥，陆 希，王 亮，吴嘉懿

（1. 浙江大学 化工系，杭州 310027；2. 上海卫星工程研究所，上海 200240）

碳纤维复合材料卫星杆件优化设计

郑传祥1，陆 希2，王 亮1，吴嘉懿1

（1. 浙江大学 化工系，杭州 310027；2. 上海卫星工程研究所，上海 200240）

基于微观力学失效分析，对碳纤维复合材料卫星支架二力杆件进行了优化设计。结果表明，与现有二力杆件相比，通过优化设计的二力杆件可以实现减质量30%以上，而强度保持不变。最后通过多个试件的试验加以验证，该优化设计案具有较好的可行性。

碳纤维复合材料；卫星；杆件；优化设计

0 引言

卫星对质量十分敏感。据资料显示，每减少1 kg质量，可以减少推进燃料150 kg，因此对卫星结构减重具有十分重要的经济价值。卫星上有很多杆件结构，如天线支架的伸缩杆件，仪器仪表的支撑结构等。杆件结构的受力特点是绝大多数杆件为二力杆件，即为受拉或者受压杆件[1～9]。为了减轻质量，这类杆件已经采用了轻质和高强的碳纤维复合材料（CFRP）。虽然CFRP的制造方法并不难，但是复合材料的核心技术难点是如何设计。目前我国对复合材料计算方法主要以传统有限元计算宏观力学强度为主，将复合材料近似以各向同性材料进行计算，而没有考虑到复合材料的非线性特性。目前国外逐步发展复合材料基于微观力学失效（MMF）分析的强度理论，充分考虑了材料的各向异性和非线性，比较真实反映复合材料的失效过程[10～12]。本研究基于微观力学失效MMF分析对卫星杆件进行优化设计，以进一步减轻杆件质量，最后对杆件进行拉伸和压缩试验加以验证。

1 基于微观力学失效的优化设计原理

复合材料最大的优点是可设计性,其次是高强和轻质，因此被广泛应用于航空航天飞行器、体育运动器材等广泛领域。其另一个特点是本构关系的复杂性，由于其各向异性，复合材料在外载荷作用下，层合板的各层上即使应变相同，应力大小相差很大，应力低的层并不比应力高的层安全。复合材料在单向拉伸载荷作用下的应变如图1所示，对复合材料给定一个应变，各向同性材料的应力是相同的；而对于各向异性的复合材料，相同应变下的复合材料各层上的应力分布会相差很大：如图中所示0°方向纤维上的应力最大，而90°方向纤维上的那一层应力最小，但是该层基体上的应力最大。因此无法用各向同性材料上的常规应力大小准则来判定复合材料的失效，即应力最小的那一层并不一定最安全，而应力最大的那一层并不一定会首先失效，相反应力最小的那一层完全有可能基体先失效。复合材料合理的方法是对复合材料结构进行逐层失效分析，最后确定哪一层首先失效，这就是基于微观力学失效的分析方法。

计算复合材料每一层的微观力学过程十分复杂，由于复合材料可变参数众多，无法用一般的解析方法计算众多的本构关系，因此需要借助专门的计算软件进行计算。对复合材料进行设计时还需要考虑采用什么强度理论，国际上应用最广的是著名Tsai-Wu强度理论[11,13～16]，该强度理论同样为本研究的分析设计所采用。

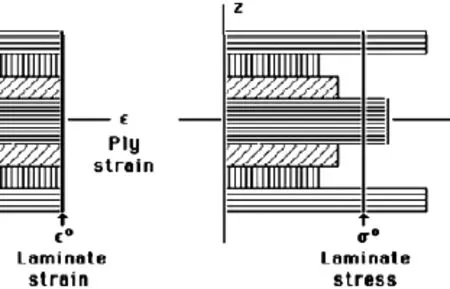
图1 复合材料拉伸后应变图Fig.1 unidirectional stretchingstrain plot of compositelaminates

为了便于设计，将复杂的本构关系计算和每一层的失效判断均转化为对每一层的强度因子R的判断，R定义为最大允许应力（应变）/实际应力（应变）之比，对于每一层复合材料，当R＞1的时候，该层复合材料是安全的，当R＜1的时候，该层复合材料是不安全的，所以R=1是一个临界状态，为了使结构安全，R必须＞1[17]，图2为复合材料强度因子R的示意图。

将复合材料复杂的本构关系计算转化为基于Excel强大计算功能的计算程序，可以使复杂的计算得到大大的简化，美国著名学者Stephen W. Tsai编写了基于Tsai-Wu失效理论的MIC-MAC计算软件，该软件一共有10 个功能模块可供选择，根据复合材料的受力情况和复合结构的不同可以选择不同的计算模块，材料可以从软件自带的常用复合材料库里选择，也可以根据用户自己的选择自行定义材料。对于不同的敷设角度和复合方法，总有一个确定的敷设角度和复合层数，使得R值最大，此时的复合方法结构最安全。

2 卫星杆件的优化设计

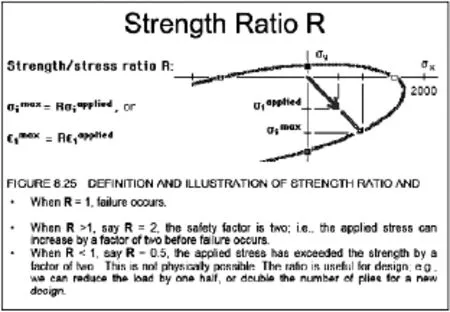
图2 强度比例因子RFig.2 strength ratio R of composite material

2.1 理论计算

首先以一个实际使用中的卫星杆件载荷为例，该杆件直径φ50 mm，长度1 000 mm，两端受拉力1×105MN/m，铺层方式为（0/45/-45/90）7，壁厚为2.8 mm，材料为T300/5208。

用MIC-MAC软件对该CFRP杆件进行计算，首先按照原铺设方法（0/45/-45/90）7进行计算，计算该结构的每一层的R值。由于该结构是非对称铺设层合板，采用MIC-MAC软件中的GenLam计算模块，7 组（0/45/-45/90）7重复铺设，一共是28 层。计算结果如图3所示，最小R值为1.53，有一定裕量，可见仍有进一步减重的潜力。

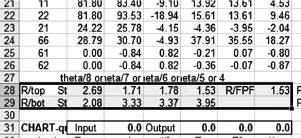
图3 R的计算结果Fig.3 R Calculated Result

2.2 杆件的优化设计

从以上的计算可以看出，即使按照目前的铺设方法，该卫星杆件仍有进一步减重的潜力。接着，通过计算可以进一步判断目前的铺设方法是否合理，可通过MIC-MAC软件进行计算比较，以得到在保证强度需要的前提下最少的复合层数，以最大限度地减轻卫星杆件的质量。

通过计算分析发现，在承受轴向单向载荷的情况下，在保证强度足够的情况下，即R值≥1的时候，（0/45/-45）的铺设方法可以比（0/45/ -45/90）的铺设方法少4 层。现计算当铺设角度为（0/45/-45）s时，最小所需的铺设层数。其他参数保持不变，以复合层数为变量（即复合次数从1 次到6 次，或者更多），对R的结果进行计算，可以看出，只要2×2×3=12 层对称铺设后，其强度即可达到要求，即R＞1；即使R达到1.5的时候也只要18 层，比此前的原铺设方法28 层要减少10层，可见减重效果十分显著[18]。因此本研究选用（0/45/-45）2s对称铺层作为试件。

3 试验与讨论

按照以上的优化结果，试制了1 根 20 mm内径的CFRP管子，材料为T300/5208，铺设方法为（0/45/-45）2s，试件如图4所示。

试验是在美国进口的MTS600万能试验机上进行的，如图5所示。试件长度100 mm，安装在试验机上情况如图6所示。试验一共做了5 组，压缩失效的载荷分别为18.8，19.0，18.9和19.0 kN，失效后CFRP管子见图7所示。理论计算结果如图8所示，当R=1.0时，最大轴向载荷为-0.31 MN/m，合计19.78 kN，与实验结果有少量误差，但是一致性较好。误差存在的原因是国内树脂性能在实际固化后均比对应理论值偏低。

图4 CFRP管子试件Fig.4 Test samples of carbon composite tube

图5 MTS600试验机Fig.5 MTS Test machine

图6 试件安装图Fig.6 Installation of Test sample

图7 CFRP管子失效图Fig.7 Picture of failed tube

图8 理论计算结果Fig.8 R Result from Mic-Mac

4 结论

从理论优化设计和试验结果可以看出，对于卫星结构等使用的复合材料二力杆件，在拉、压二力载荷作用下，（0/45/-45/90）对称复合铺设方法的强度比（0/45/-45/90）非对称复合铺设方法要好，（0/45/-45）s对称复合方法的强度要好于（0/45/-45/90）对称复合方法。在保持相同强度的条件下，承受同样载荷作用下，与未经优化设计的原杆件相比，采用相同材料，复合材料的层数可以从28 层降低到18 层，减质量可达30%以上。经过对5 组材料为T300/5208（0/45/-45）2s对称铺设的复合材料压缩试验验证，理论分析具有较好的可靠性和一致性。

[1] 王海明, 赵华, 杨文涛. "资源一号"卫星某星敏支架力学性能分析[J]. 航天器环境工程, 2007, 24(3): 168-173.

[2] 赵秋艳, 沃西源. 复合材料在国内外卫星结构上的应用概况[J]. 航天返回与遥感, 2000, 21(1): 53-57.

[3] JORGE A. C. AMBRÓSIO. MARIA AUGUSTA NETO AND ROGÉRIO PEREIRA LEAL，OPTIMIZATION OF A SATELLITE WITH COMPOSITE MATERIALS[M]. MATHEMATICAL SCIENCES PUBLISHERS, 2007: 1 397-1 419.

[4] Han Jianping, Qin Yingjie, Gao Wei, et al. MinEffects of thermal cycling on mechanical and physical properties of high performance carbon/epoxy composites applied to satellite antenna[J]. Proceedings of the International Astronautical Congress, 2014, (8): 5 859-5 866.

[5] 王建昌, 安庆升, 叶周军, 等. 碳纤维复合材料卫星天线的研制[J]. 纤维复合材料, 2007, 3(2): 18-19.

[6] 肖少伯. 碳纤维及其复合材料在卫星上的应用[J]. 高科技纤维与应用, 1999, 24(2): 1-7.

[7] 李威, 郭权锋. 碳纤维复合材料在航天领域的应用[J].中国光学, 2011, 4(3): 201-212.

[8] 林益明, 杨宝宁. 三维编织复合材料在卫星支架的应用[J]. 航天器工程, 2002, 11(4): 29-33.

[9] T. Gerhard, C. Friedrich. Mechanical fastening of carbon composite tubes, numerical calculation of axial loading capacity and experimental verification[J]. Composites: Part B, 2014, (67): 391-399.

[10] Hana, P., Inneman, A., Daniel, V., et al. Mechanical properties of carbon fiber composites for applications in space[J]. Proceedings of SPIE-The International Society for Optical Engineering, 2015.

[11] Stephen W. Tsai. Composite design: Strength and life prediction[M]. ISBN: 0961809000，2012；

[12] 章令晖, 陈萍. 先进树脂基复合材料在卫星天线系统中的应用[J]. 宇航材料工艺, 2011, (4): 1-5.

[13] 周志成, 曲广吉, 黄海. 某卫星平台多结构工况下的优化设计[J]. 北京航空航天大学学报, 2009, 35(7): 821-823.

[14] 陈昌亚, 王德禹. 集主承力结构与大容量储箱支架于一体的卫星主承力筒结构研究[J]. 空间科学学报, 2005, 25(2): 149-153.

[15] C. Soutis. Carbon fiber reinforced plastics in aircraft construction[J]. Materials Science and Engineering A 412, 2005: 171-176.

[16] F.L. Matthews, G.A.O. Davies, D. Hitchings, et al. Finite Element Modelling of Composite Materials and Structures[M]. Woodhead Publishing Ltd., 2000.

[17] West Stephen, White Charles, Celestino Chris, et al. Design and testing of deployable carbon fiber booms for cubesat non-gossamer applications[M]. 56th AIAA/ASCE/ AHS/ASC Structures, Structural Dynamics, and Materials Conference, 2015.

[18] 郑传祥, 魏双, 陆希, 等. 基于微观力学失效分析对碳纤维复合材料卫星支架杆件的优化设计[J]. 高科技纤维与应用, 2016, 41(1): 29-33.

Optimal design of carbon fiber composite rod used in satellite

ZHENG Chuan-xiang1, LU Xi2, WANG Liang1, WU Jia-yi1

( 1. Zhejiang University, Hangzhuo 310027; 2. Shanghai SatelliteEngineering Research Institute, Shanghai 200240 China)

Based on micro- mechanical-failure (MMF), An optimal design of the two force rod of the carbon fiber composite material used in satellite support was carried out. The results show that, compared with the existing two force rods, the two force bar which is designed by the optimized design can reduce more than 30% weight, while the strength remains unchanged. Through a number of sample tests verified that the optimized design of the case has a good feasibility.

CFRP; satellite; rod; optimal design

V214.8

A

1007-9815（2016）04-0023-05

定稿日期:2016-07-15

上海航天科技创新基金（SAST201423）

郑传祥（1968-），男，浙江绍兴人，教授，博士，主要从事复合材料结构设计与强度计算，(电子信箱)zhchx@ zju.edu.cn。