注重反思 不断总结——例谈函数值域的求法

☉江苏省海门实验学校 严敏娟

注重反思 不断总结
——例谈函数值域的求法

☉江苏省海门实验学校 严敏娟

求函数值域是近几年高考的一个热点，也是一个难点.能熟练掌握函数值域（最值）的求法就显得十分重要.笔者旨在通过对典型例题的讲解来归纳函数值域（最值）的求法，希望在我们求函数值域（最值）时有所帮助.

一、判别式法求函数值域

判别式法是高中求分式函数值域的常用方法.但由于对此方法的原理不很清楚，许多学生在解题过程中对一些条件不能正确的处理，从而导致解题出错.通过下面例题说明判别式法的原理，以及在使用过程中一些要注意的地方.

解析：由已知得yx2+2xy-3y=x2-2x+3，即（y-1）x2+ 2（y+1）x-3（y+1）=0.

当y≠1时，Δ=4（y+1）2+12（y+1）（y-1）=8（2y-1）（y+ 1）≥0，y≥或y≤-1.

例2求函数（x∈R且x≠-3，x≠1）的值域.

解析：由已知得yx2+2xy-3y=2x2+4x+1，即（y-2）x2+ 2（y-2）x-（3y+1）=0.

（1）当y=2时，得-9=0，x不存在.因此，y=2不是函数值.

（2）当y≠2时，Δ=4（y-2）（4y+1）≥0，有y＞2或

对于函数值域中遇到的问题，只有清楚题目的来龙去脉，搞清原理，才能避免胡乱套用，从容应对各种类型的变化.只有这样，才算是真正掌握这种方法了.

二、变量代换法求函数值域

代换就是用一个广义数学式（可以是字母、式子、函数等）在相等条件下代替一个数或广义数学式，代换须保域，即代换前后的数学式取值范围不变，代换将改变问题的结构形式，实现转化.

例3求函数的值域.

解法一：（三角代换）由5≤x≤8，保持原函数中x的取值范围，以一三角式代换变量x，设x=5+3sin2θ，θ∈得由θ-得故函数的值域为

解法二：（双变量代换）注意到与的关系，又可作双变量代换，设则3u2+v2=9（u≥ 0，v≥0），y=u-v.如图1，在直角坐标系uOv中，由直线u-v-y=0与椭圆弧3u2+v2=9（u≥0，v≥0） 有公共点时，y∈［-3，故所求函数值域为

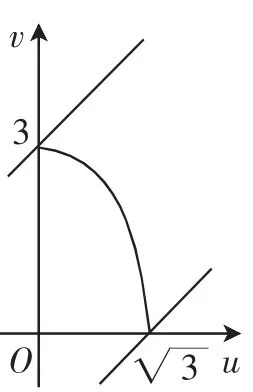
图1

变量代换关键要抓住式子的特征和结构形式进行转化.

三、构造向量求函数的值域

对于一类无理函数的值域问题，若能灵活运用向量知识，则可非常顺利地求解.避免心理上的畏惧感.下面从一个例题出发，从向量的角度谈谈这类无理函数的值域的处理，期望得到一个统一方法.

例4求函数的值域.

解析：因为构造向量a=（1，1），b=（s，t）=我们不妨把向量a，b的起点设在坐标原点，那么向量b的终点轨迹方程是2+t2=1，它的轨迹是s2+t2=1 s≥0，t≥0），在第一象限及坐标轴上的圆弧（如图2）.由则y=a·b=|a||b|cos=图易知，当向量a与向量b同向时，a与b的夹角最小，ymax=当向量b=（1，0）或b=（0，1）时，向量a与向量b的夹角最大，ymin=a·b=2×1+0×1=1.所以

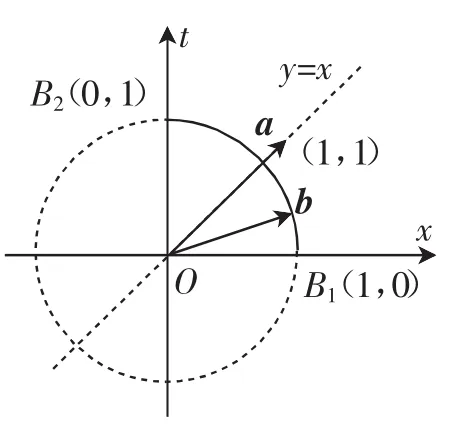
图2

（2）两个被开方数之和为正常数，即（x+b）+（c-x）=k（k为大于0的常数）.

四、直接平方法求函数值域

当两个根式的平方和为定值时，可以采用直接平方，将变量集中到一个根式中.

例5求函数的值域.

分析：本题用三角换元的主要原因是两个根式的平方和为定值，换个角度——直接平方就可以使变量都集中到一个根式中，即这样就转化为了我们熟知的一元二次函数值域的问题（具体解法略），当然用此法时事先要能控制y的符号.

五、通过有理化求函数值域

若两个根式求值域时，直接平方无法达到升幂的效果，可以考虑对函数有理化.

例6求函数的值域.

分析：本题直接平方不能使变量都集中在根号中，也无法通过以上的手段达到升幂的效果，此时就从函数的性质角度思考，有理化后可直观发现此函数有单调性在定义域内为单调增函数，再求定义域，根据单调性解决.

六、数形结合或式子的几何意义求函数值域

这类求解的式子具有明显的几何意义或特定的结构特征，根据函数图像、性质能较容易得出值域（最值）的简单函数.

例7已知p（x，y）是圆x2+y2=4上的点，试求t=x2+y2-3xy的值域.

分析：在三角函数章节中我们学过sin2α+cos2α=1，注意到x2+y2=4可变形为sinα，α∈［0，2π），则t=4-3×2cosα×2sinα=4-6sin2α.又2α∈［0，4π），即sin2α∈［-1，1］，故t∈［-2，10］.

例8求函数的值域.

分析：看到该函数的形式，我们可想到已知两点求直线的斜率的公式将原函数视为定点（2，3）到动点（cosx，sinx）的斜率，又知动点（cosx，sinx）满足单位圆的方程，从而问题就转化为求点（2，3）到单位圆连线的斜率问题，作出图形（如图3），观察易知最值在直线和圆上点的连线和圆相切时取得.设切线方程为y-3=k（x-2），即kx-y+3-2k= 0，从由于原点（0，0）到切线的距离等于半径1，则有1=解得所以y∈

点评：本题从函数本身的形式入手，引入直线的斜率，结合图形，从而使问题得到巧解.

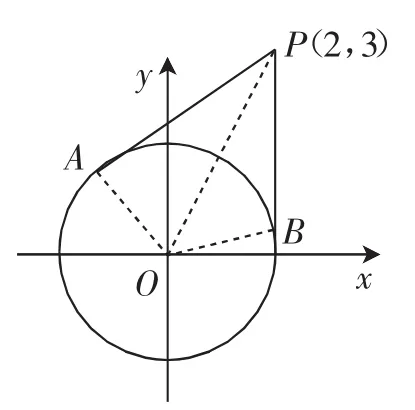
图3

七、通过线性规划求函数值域

例8求函数y=的值域.

解析：（数形结合法）由x∈［-3，1］，令u=则在平面直角坐标系uOv中，作出圆弧u2+v2=4（u≥0，v≥0）和直线y= u+v，（u≥0，v≥0），如图4所示，故得最大值为最小值为2.

通过教学思想方法的运用，突出了函数的一个性质，值域，让学生领悟了函数、数形结合、转化与化归的数学思想方法.解题教学不应重视一招一式，而应注重方法的自然性、普适性，以及解题后的反思、提炼.因此，解题教学中，教师的主要职能在于怎样帮助学生做好解题后的反思，充分挖掘例题本身的功能，做到“授之以渔”.特别是解题后在知识方法方面进行分析、比较、反思、提炼的过程，使这个例题的解题思维成为一种能力，而并不是只注重这个题的步骤是什么，这个思维的突破要是自然的，有普适性，最后让这些解题的思维方法、意识留在学生的脑海中，这样的例题教学才是有效的.

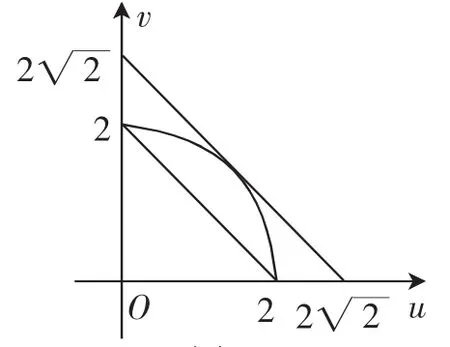
图4