追求教学实效，拓展高中生的数学思维能力

☉江苏省扬州市邗江区蒋王中学 严高明

追求教学实效，拓展高中生的数学思维能力

☉江苏省扬州市邗江区蒋王中学 严高明

数学教学进入到高中阶段之后，师生们看待知识的视角都应当提升一个新的高度.高中数学的教学目标，不再仅仅聚焦于具体的知识内容之中，而是要扩展到思维能力的层面.学生们只有在熟练掌握知识内容（基础知识）的量变，才能收获思维能力显著提升的质变.与此同时，也只有学生们的数学思维能力增强了，才能更好地推动其完成更加高效优质的知识学习.二者之间相辅相成的紧密关系也向教师们进一步明确了将拓展学生数学思维能力作为高中数学教学阶段一个突出教学目标的重要性.

一、展现知识趣味，激发学习兴趣

兴趣是最好的老师，即使是在学习压力很大的高中阶段，学习兴趣的激发对于数学学习来讲都是至关重要的.兴趣就像内置于学生心中的马达，为自主学习的开展提供着根本性动力.因此，为了能够切实提升教学实效，教师们要将兴趣激发这个前提基础打牢，并以此推动主体教学高效率开展.

例如，在对几何体三视图的知识进行教学之前，我并没有急于将这个概念呈现给学生，而是先带领大家做了一个小游戏，名为“猜猜它是谁”.我在黑板上画出了如图1所示的三幅图.一开始，学生们并没有意识到三者之间有什么联系.我却告诉大家：“你们知道吗？其实这三幅图表示的是同一个几何体.”学生们感到有些诧异，但很快感到这种图形展现方式十分新颖，并非常想要知道这个神秘的几何体究竟是什么.“好的，那就展开你们的想象力，看谁能第一个猜出这个几何体是什么吧！”在我的鼓励下，学生们立刻带着高涨的兴趣与热情投入到了几何空间的想象与思考当中，并在不知不觉中走进了几何体三视图的世界.

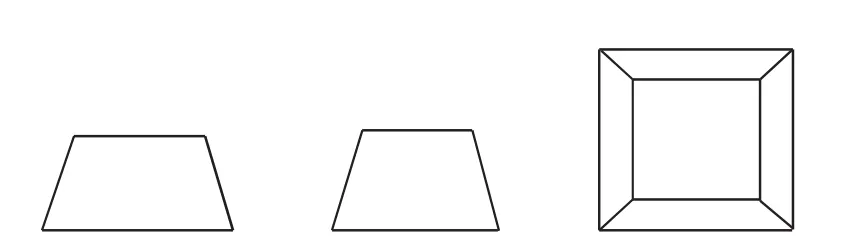
图1

表面看来，数学知识的理论性和抽象性都很强，特别是高中阶段的数学学习，知识数量大，知识难度强，让很多学生感到索然无味，甚至望而却步.这对于教学实效提升都是会产生很大阻碍作用的.其实，在看似乏味的外表之下，数学知识的学习与探索是很有乐趣的.为了让学生们可以感受到这一点，教师们可以从形式或内容入手，设计不同的教学活动来予以支撑，将学生们的思维热度从教学开始之初调动起来.

二、注重知识积累，加强活学活用

我们常说，只有量变到一定程度，才能引发质变.具体到高中数学教学当中，学生们只有实现了一个个具体知识内容的持续积累，方能达到思维能力的提升.而这里所说的能力提升的一个重要表现，就是能够将所学知识活学活用.只有能将基础知识灵活理解并运用起来，才是真正将数学学懂了、学活了.这也是与数学学科的自身特点相呼应的.

例如，在学习不等式的知识时，学生们曾经遇到了这样一个问题：解不等式3<|2x-3|<5.这是一个很有典型性的问题，包含着很强的思维灵活性.于是，我要求学生们尽可能多地找到这个问题的解答方法.果然，大家在我的启发之下，经过讨论先后找出了如下几种解题方法：第一，根据绝对值的定义，进行分类讨论求解，即对2x-3≥0和2x-3<0两种情况分别求解，最后取并集.第二，将原式转化为不等式组求解，即将之转化为|2x-3|>3且|2x-3|<5.第三，利用等价命题法，使得原式等价为3< 2x-3<5或-5<2x-3<-3，进而求解.第四，利用绝对值的集合意义，将原式转化为该不等式的几何意义就是数轴上的点x到的距离大于，且小于于是，简单画出图2所示的数轴图形，答案便轻松可得.这个问题的解答过程，是十分典型的由知识积累所实现的活学活用.不难发现，在上述四种解题方法的探索之中，学生们分别运用了不等式、数轴等具体知识，还调动起了分类讨论、转化思想、数形结合等思想方法，可谓灵活且丰富.

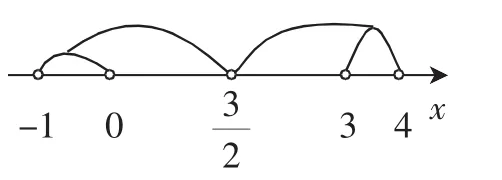
图2

数学本来就是灵活的，这既是数学学习的难点所在，也是这一学科的魅力所在.对于刚接触新知识不久的学生来讲，通过自己的力量将之灵活运用并不容易，这便需要教师的适时介入和积极引导.通过变式问题的设计提出，于潜移默化当中开启学生们的思维大门，让他们在解答问题的同时从多个角度深刻认知数学内容，逐步走向深入学习.

三、开展小组合作，相互弥补提升

人们常说，团结就是力量.这句话在高中数学的学习当中同样适用.面对灵活多变的数学知识，仅靠一个人的思维往往无法将其穷尽.对于一些新问题和新情况，即便是教师也难以做到考虑周全，万无一失.这时，就需要借助集体的力量.对于一些较为复杂、疑难的问题，采取小组合作的学习方式，让组内学生分别发表看法的同时实现思维的碰撞，相互启发，取长补短，不仅能够大大提升自主学习效率，有时还会发现知识的新大陆.

例如，在正方体内容的教学过程中，我为学生们设计了这样一个问题，并请大家在小组内共同进行讨论：如图3所示，点E、F分别为正方体的面ADD1A1和面BCC1B1的中心，则四边形BFD1E在该正方体的面上的射影是什么？学生们都觉得这个问题很简单，可是，每个小组得出的结论却不一样.有的小组认为，射影是一个平行四边形，有的小组则认为，射影是一条线段，有的小组同时提出了上述两种答案.这个差异化的效果正是开展小组合作所需要的.就此，我引导学生们对每组的结论进行思考，判断出哪一种是正确的.也正是在这个过程中，大家对知识的理解得到了完善与深化.

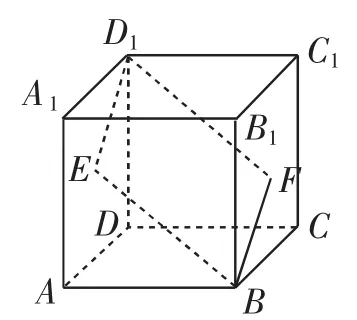
图3

应当强调的是，小组合作学习并不只是针对于学生自身而言的，教师的巧妙融入也至关重要.既然是要通过合作讨论的方式探求知识，那么，这之中的每一个个体就都应当站在平等的位置上.教师在这之中也是参与讨论的一员，绝不能立于合作活动之外.当然，根据不同知识内容的特点及教学目标的不同，教师们可以选择不同的参与方式，既可以起到引导启发的作用，也可以参与到推理活动当中去.

四、大胆尝试开拓，勇于开放探索

当然，对于高中数学来讲，始终停留在基础知识内容的范畴之内是远远不够的，学生们还需要继续拓展思维，开阔思路，将知识的版图进一步扩大，走出教材，高效运用.这是优质的高中数学教学所追求的升华目标，对于学生们知识学习的长远发展也是具有积极意义的.落实到实际教学当中，教师们要做的就是为学生们打开开拓的大门，为他们尽可能多地打造知识探索的宽广平台.

例如，在圆的学习过程当中，当学生们学习过基本内容之后，我大胆将问题向灵活的方向进行了开放式改变：已知点P是直线3x+4y+8=0上的动点，PA和PB是圆x2+ y2-2x-2y+1=0的切线，点A、B是切点，点C是圆心，那么，四边形PACB面积的最小值是多少？通过向基本问题当中加入了“动点”和“最小值”这两个元素，从解题过程本身到数学思维逻辑都发生了十分显著的变化.学生们需要打破既有的定式思维，采用开放性的眼光去分析问题.这不仅是数学提问的创新，更是引领学生们走进了更为深入的数学思考当中.以这种方向将问题继续灵活开放，将会收获愈发理想的教学效果.

探索性问题往往具有很强的开放性与灵活性，也经常成为学生们抵触和惧怕的对象.对此，教师们一定要及时鼓励学生，并带领大家迎难而上，采取灵活巧妙的方式，让学生们逐渐习惯开放式的思维模式，进而将知识探究视为高中数学学习的常态.当然，教师也要严格把握这类问题的设置难度，一方面，要让学生们易于接受，不致失去学习自信；另一方面，也要在其中加入挑战性元素，带领学生们将知识能力迈上更高台阶.

相比于具体知识内容的呈现来讲，提升学生数学思维能力显然是一个比较抽象的课题.为了将这个较深层次的教学内容落实好，教师们需要从数学教学的各个环节入手进行创新性设计.不仅要关注主体知识学习，还要关注学习心理构建；不仅要关注基本知识内容，还要关注方法归纳与开放拓展.只有这样，才能实现全面的教学方式优化，切实达到教学实效的有效提升.当然，具体的教学措施还有许多，随着时代的不断发展还会继续灵活变化，等待广大高中数学教师们去发现和应用.