基于改进的多层小波分解压缩感知图像处理*

翁天阳，庄 宇，刘云飞

(南京林业大学 信息科学技术学院，江苏 南京 210037)

基于改进的多层小波分解压缩感知图像处理*

翁天阳，庄 宇，刘云飞

(南京林业大学 信息科学技术学院，江苏 南京 210037)

为了改进图像恢复效果，减少运行时间，提出了一种基于改进的多层小波分解压缩感知图像的处理方法。该方法利用小波变换对图像进行多层分解，根据小波域高频系数分布特点通过高斯矩阵随机观测，利用正交匹配追踪算法(OMP)恢复高频系数，最后通过小波逆变换重构图像。实验结果表明，本文的算法优于传统算法，峰值信噪比(PSNR)平均提高了4～6 dB，运行时间缩短了1～2个量级，为物联网、无线传输技术提供了更好的可能性。

压缩感知；多层；分块；小波变换；高斯矩阵；正交匹配追踪算法；重构

压缩感知理论是在2006年由Donoho、Candes等在相关研究基础上正式提出的[1-3]， 压缩感知的基本思想就是当信号在某一正交变换基上能够稀疏化表示或者能在特定的域中转换成稀疏信号，利用较少的观测信息重构出原始信号。压缩感知方法直接对原始信号进行随机观测。因观测量小于原信号，因而在采样的同时对信号实现压缩，即对信号低速采样[4-5]，最后通过重构算法恢复即可。这一理论一经建立便在信号处理领域、通信领域、医疗医学成像技术领域收到了较高的关注度[6-7]，具有重要的实践意义。

1 压缩感知理论

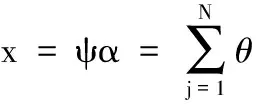
(1)

将N维信号投影到M维中，用观测矩阵φ观测稀疏域得到观测向量y。

y=φα=φψTx.

(2)

通过求解α就可以得到信号x。由于维数M远远小于信号的长度N，因此必须求解欠定方程组，Tao等人证明若式(3)成立，则观测矩阵满足RIP性质，方程可以有唯一解。

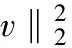
(3)

式中，δ∈(0，1)称为RIP常数。因此，可以将求解欠定方程组这一问题转化为求解l0范数下的最优化问题。即

min‖x‖0s.t.y=φx.

(4)

求解l0问题可以进一步转化为求解l1的凸优化问题，即

min‖x‖1s.t.y=φx.

(5)

求解式(5)常用的算法有贪婪算法和迭代阈值算法。正交匹配追踪算法(OMP)是贪婪算法的一种，也是具有广泛性的一种算法。

2 基于空域分块的小波变换压缩感知算法

传统的压缩感知算法在重构时每次只能在观测矩阵中选取一个原子处理，重建过程非常缓慢，当随着迭代次数的增加，总体消耗的时间也将大幅度增加。为了提高整体运行速度。这里将原本256×256的图像分成32×32图像块，然后利用对每个图像块进行二维小波分解，保留每块小波域的LL部分，对其余三块高频子块单独进行高斯随机观测，然后对三个高频子块依次重构，最后通过二维小波反变换得出空域图像。

本文在图像重构时采用是正交匹配追踪算法(OMP)，具体算法描述如下：

输入：观测矩阵φ，观测向量y，稀疏度k

初始化：残差r0=y，索引集Λ0=∅，n=1

3) 最小二乘法近似求解

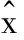
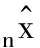
5) 判断n是否大于k，若大于，则停止迭代，否则继续迭代。

3 基于小波域分块的多层小波变换的压缩感知算法

上述空域分块等同于对图片加了几个矩形窗，这必然会导致频谱泄露，因此本文采用在小波域分块的方法来减少边界信息的丢失。本算法首先对整幅图像进行多层小波变换，将图像分成LL，HL，LH，HH，HLLL，HLHL……。然后针对小波域中不同的区域采用不同的观测矩阵，以此来提高图像的整体压缩比和改进压缩效果。

本文选用8×8的块图像。分块压缩观测算法的数学表达式见(6)、(7)、(8)。

(6)

(7)

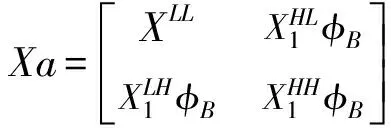
(8)

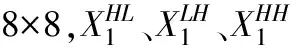
一个M×N的高斯矩阵的每一个元素都满足N(0，1/N)的独立正态分布，它几乎与任意的稀疏信号都不相关，因此所需要的测量次数很小，是较常用的CS观测矩阵。

哈达玛(Hadamard)矩阵也用作CS观测矩阵，它是由+1和-1两种元素构成的且满足Hn*HnT=nI，其中HnT为Hn的转置，I为单位方阵，n为阶数。在N×N的哈达玛矩阵中随机地选取M行向量，构成一个M×N的观测矩阵。

采用多层小波分解保留了全部低频信息，而在高频区域则根据HH，LH，HL……稀疏度逐渐升高，观测矩阵的M值也逐渐加大。较单层小波算法，整体性提高，消除了块效应。

4 实验结果分析

根据第二节方法，分别对256×256的Lena、barbara图进行测试，利用随机高斯矩阵和部分哈达玛矩阵进行随机观测，重构图像时采用正交匹配追踪算法(OMP)。依次选取M/N分别为25%、30%、40%、50%、60%、75%来仿真，分别对传统的OMP重构算法、改进的空域分块的小波变换压缩感知算法以及本文提出的小波域分块多层小波变换压缩感知重构算法进行仿真分析。

首先，对Lena图进行三种算法的比较，在不同压缩比下记录峰值信噪比以及观测比为50%时运行的平均时间。结果如表1所示。从表1可知，本文的算法优于传统算法，运行速度提高了1～2个量级，峰值性噪比提高了4～6 dB。

最后，采用本文算法利用高斯随机观测对Lena、Barbara两幅图像进行恢复。图1为Lena处理图像，(a)为原始图像，(b)、(c)、(d)分别为观测比为25%、50%、75%时的恢复图像。图2为Barbara处理图像，(e)为原始图像，(f)、(g)、(h)分别为观测比为25%、50%、75%时的恢复图像。

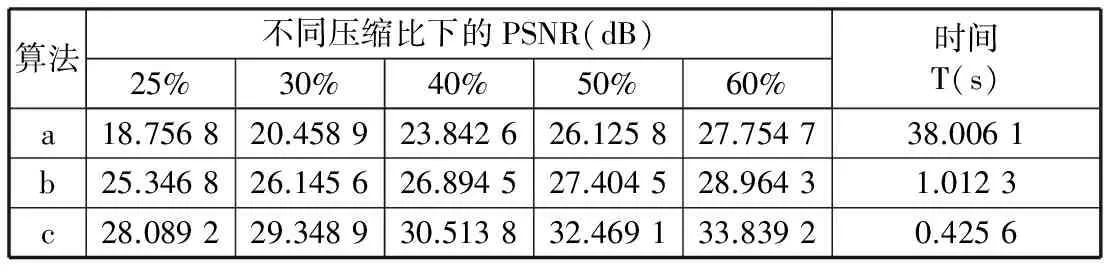
表1 三种算法比较

观察图1，图2，我们得知，Lena图在50%的观测比时就有较好的恢复效果，而Barbara图在75%的观测比时图像才清晰。因为Lena图属于较为平滑的图像，图像信息主要集中在低频区域，而Barbara图像在高频区域成分较多，在随机观测时损失了较多的高频信息，恢复效果稍差。

(a) (b) (c) (d)

图1 Lena图不同观测比恢复效果

(e) (f) (g) (h)

图2 Barbara图不同观测比恢复效果

5 结束语

本文提出了一种在小波域分块，并采取多层小波变换的压缩感知的重构算法，经过多层小波分解后，根据提取的低频、中频、高频特点进行随机观测，解决了空域分块造成的信息泄漏问题。通过实验表明，本文算法与传统的压缩感知方法相比，峰值信噪比平均提高了4～6 dB，并且在运算时间上，缩短了1～2个量级，非常适合应用于硬件的实现，并为物联网、无线传输技术提供了更好的可能性。

[1] Donoho DL.Compressed Sensing[J].IEEE Trans. on Information Theory,2006,52(4):1289-1306.

[2] CANDESE,ROMBERG J,TAO T.Robust Uncertainty Principles：Exact Signal Reconstruction from Highly Incomplete Frequency Information[J].IEEE Trans Information Theory，2006，52(4)：489-509.

[3] Candès E J.Compressive Sampling[C].Proc. of International Congress of Mathematicians.Madrid,Spain:[s.n.],2006:1433-1452.

[4] 岑翼刚，陈晓方，岑丽辉，等.基于单层小波变换的压缩感知图像处理[J].通信学报,2010,31(8A):52-55.

[5] 练秋生，王艳.基于双树小波通用隐马尔可夫树模型的图像压缩感知[J].电子与信息学报,2010,32(10):2301-2306.

[6] 金坚，谷源涛，梅顺良.压缩采样技术及其应用[J].电子与信息学报，2010，32(2):470-475.

[7] 刘吉英，朱炬波.基于压缩感知的低数据率雷达采样与成像方法[J].计算机工程与科学，2012，24(5):646-651.

[8] 石光明，刘丹华，高大化，等.压缩感知理论及其研究进展[J].电子学报，2009,37(5):1070-1081.

[9] 杨海蓉，张成，丁大为，等.压缩传感理论与重构算法[J].电子学报,2011,39(1):142-148.

[10] 王天荆，郑宝玉，杨震.基于自适应冗余字典的语言信号稀疏表示算法[J].电子与信息学报，2011，33(10)：2372-2377.

[11] 李炳杰，吕园，叶萌，等.基于非相干准则的压缩感知观测矩阵设计的极大极小方法[J].空军工程大学学报：自然科学版，2011，12(5)：81-85.

Compressed Sensing Image Processing Based on Improved Multi Layer Wavelet Decomposition

Weng Tianyang, Zhuang Yu, Liu Yunfei

(CollegeofInformationScienceandTechnology,NanjingForestryUniversity,NanjingJiangsu210037,China)

In order to improve the effect of image restoration and reduce the operation time, a compressed sensing method based on improved multi-layer wavelet decomposition is proposed. The image is divided into multi-blocks by multilayer wavelet transform and the Gaussian matrix is used to observe the high frequency based on the characteristics in domain. For the reconstruction, high frequency can be recovered by the matching pursuit algorithm (OMP) and the image can be reconstructed by the inverse wavelet transformation. Simulation results demonstrate that the proposed algorithm is better than the traditional algorithm, and the PSNR is improved about 4～6 dB, and the operating time is shortened about 1～2 magnitude. It provides a better possibility for Internet of things and wireless transmission technology.

compressed sensing; multi layer; blocks; wavelet transform; Gaussian matrix; matching pursuit algorithm; reconstruction

2016-09-30

国家自然科学基金(31170668)

翁天阳(1992- )，女，江苏启东人，硕士研究生，主研方向：信号处理。

1674- 4578(2016)06- 0005- 02

TP391.41，TN911.72

A