一种高效的模式串匹配算法
赵 晓, 何立风, 王 鑫, 姚 斌, 巢宇燕, 王亚妮
(1.陕西科技大学 电气与信息工程学院, 陕西 西安 710021; 2.日本名古屋产业大学 环境商务信息学院, 爱知县 尾张旭市 488-8711)
一种高效的模式串匹配算法
赵 晓1, 何立风1, 王 鑫1, 姚 斌1, 巢宇燕2, 王亚妮1
(1.陕西科技大学 电气与信息工程学院, 陕西 西安 710021; 2.日本名古屋产业大学 环境商务信息学院, 爱知县 尾张旭市 488-8711)
基于BM算法和Horspool算法,提出了一种简单且高效的模式串匹配算法.将匹配成功部分的每个字符作用于坏字符移动策略以获得多个移动参考量,从这多个参考量中选择最大值作为模式串的当前移动量.模式串在每个不匹配位置的移动量可以仅根据模式串预先计算获得.实验结果表明,该算法在任意不匹配位置所给出的移动量均是当前模式串的最大移动量,提高了模式串匹配的效率.
模式匹配; 字符串匹配; BM算法; Horspool算法
0 引言
模式串匹配操作是计算机科学领域中的一种基本运算,常用于解决在一个大文本中查找给定模式串是否存在的问题.模式串匹配操作被广泛应用于信息检索、病毒检测、计算生物学、拼写检查等研究领域.提高模式串匹配处理效率是信息科学和计算机科学领域的重要研究之一[1].
从1977年至今,在模式串匹配问题上取得了许多的研究成果,其中最著名的算法是Boyer-Moore(BM)算法[2].自从BM算法提出后,研究者对其进行了许多改进[3-8],Horspool算法为最有效的简化算法之一[3],且在入侵检测中有较好的应用[9].
本文结合BM算法和Horspool算法处理中的坏字符策略,提出一种高效、简单的模式串匹配算法.当不匹配发生时,新提出算法确保了模式串向前的移动量总是最大值.实验结果表明,该算法要比Horspool算法更加有效.
1 BM算法和Horspool算法的基本原理
为了描述方便,在本文的图中用text表示文本串;用pattern表示待匹配的模式串;当前用于匹配的文本子串用t[i]…t[i+m-1](0 ≤i≤n-m),其中i表示当前文本子串的起始位置,n表示文本串的长度,m表示待匹配子串的长度;模式串pattern中的字符用p[0]…p[m-1]表示,其中m用于表示模式串的长度.
1.1 BM算法基本原理
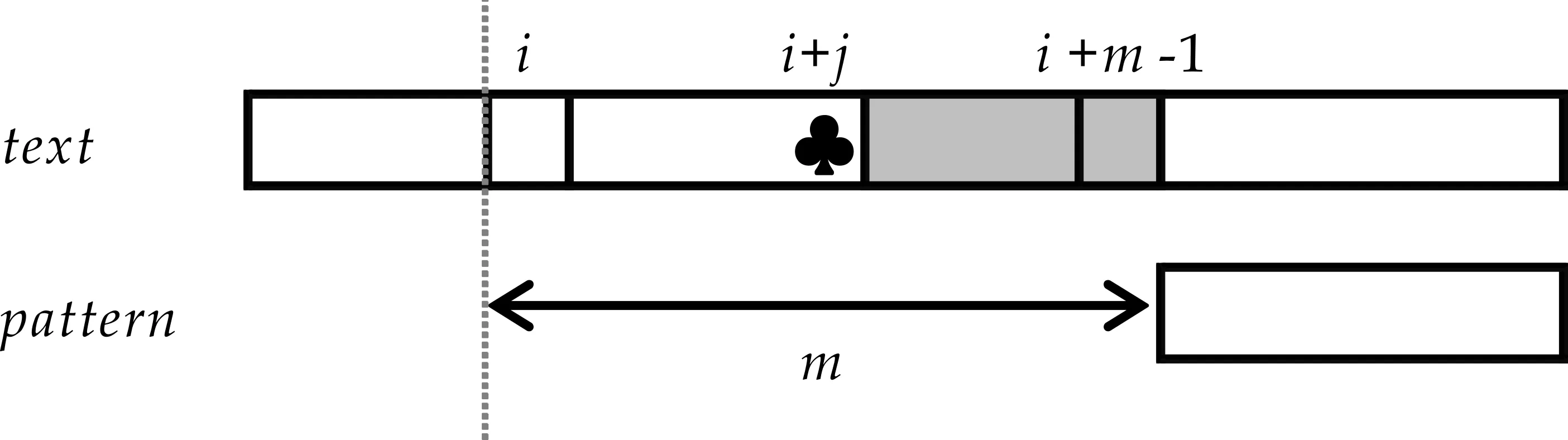
1977年,Boyer和Moore提出了著名的BM模式串匹配算法[2],该算法从右向左对模式串p[0]…p[m-1]和当前文本子串t[i]…t[i+m-1]进行匹配检查.当p[j]和t[i+j]不匹配发生时(图1(a)所示),BM算法通过两种策略(坏字符移动策略和好后缀移动策略)计算模式串的移动量,并选择其中的最大值作为模式串向前的移动量.
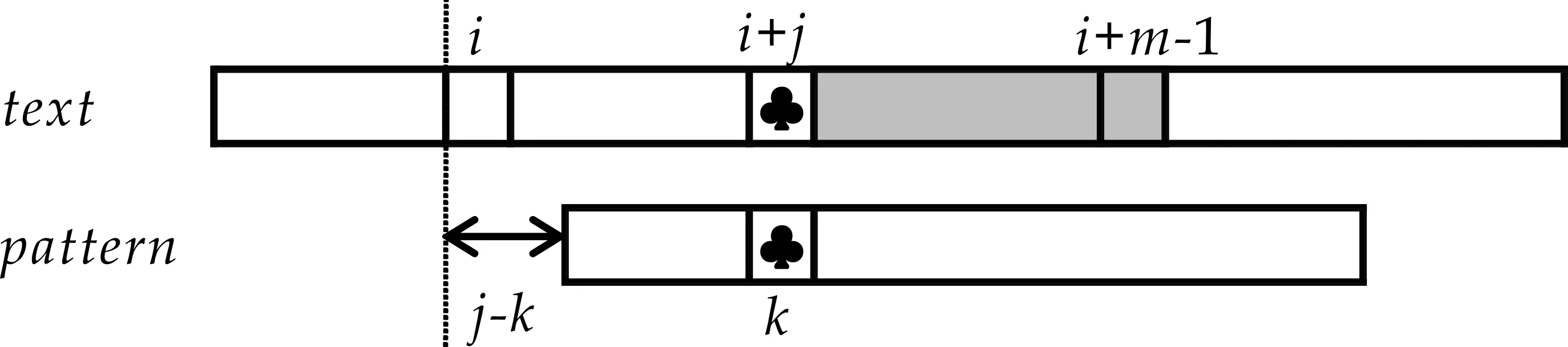
坏字符移动策略利用字符t[i+j]来计算模式串的移动量,表示为skip1[t[i+j]].当字符t[i+j]不是模式串中的字符时,由于t[i+j]与模式串中的任何字符都无法匹配,故可以将模式串向前移动至字符t[i+j]之后,使模式串的第一个字符和字符t[i+j+1]对齐.相应的模式串移动量为skip1[t[i+j]]=j+1,如图1(b)所示.另一方面,如果字符t[i+j]与模式串中的字符p[k]相同,通过移动模式串使t[i+j]与p[k]对齐时,所对应的文本子串和模式串就有完全匹配的可能,需要进一步检验.这时的模式串移动量为skip1[t[i+j]]=j-k,如图1(c)所示.很明显,根据给定的模式串,对于文本中的任何字符α,可以预先计算出skip1[α].
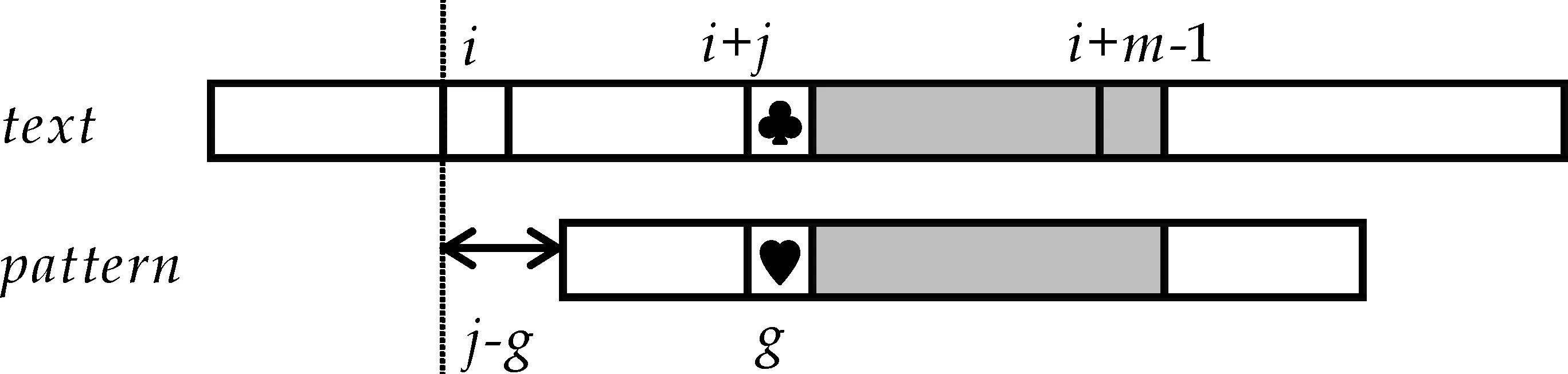
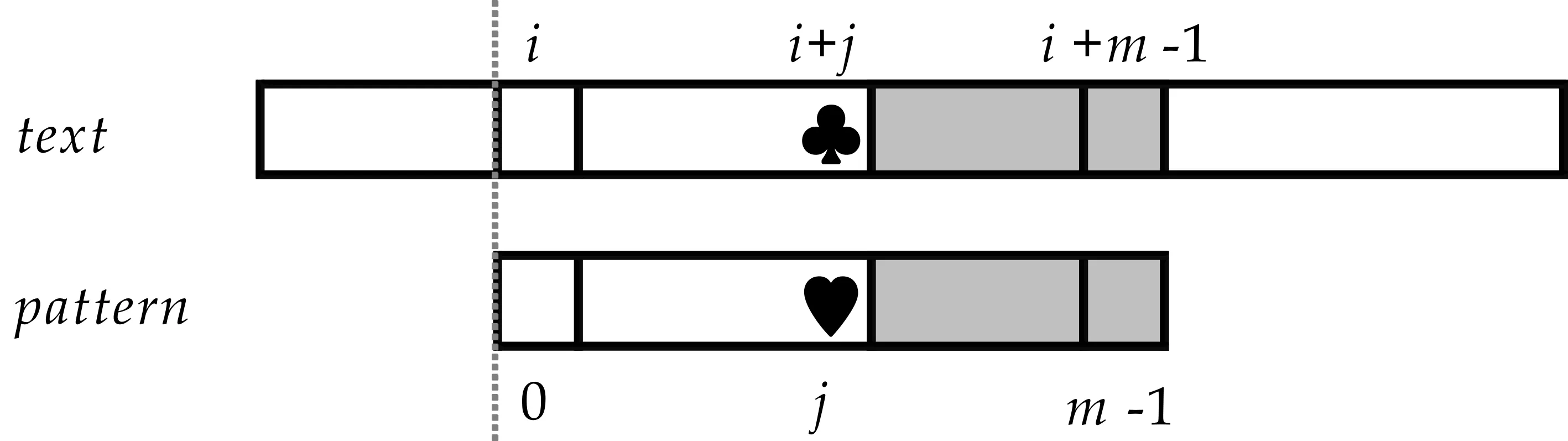
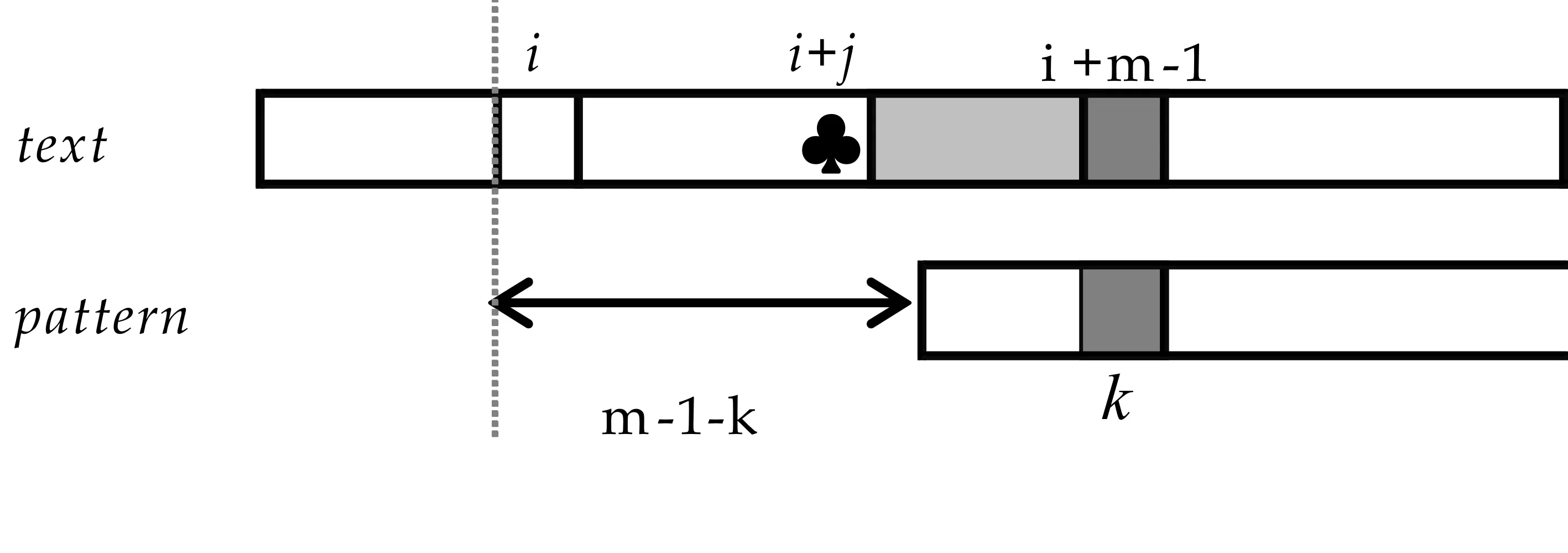
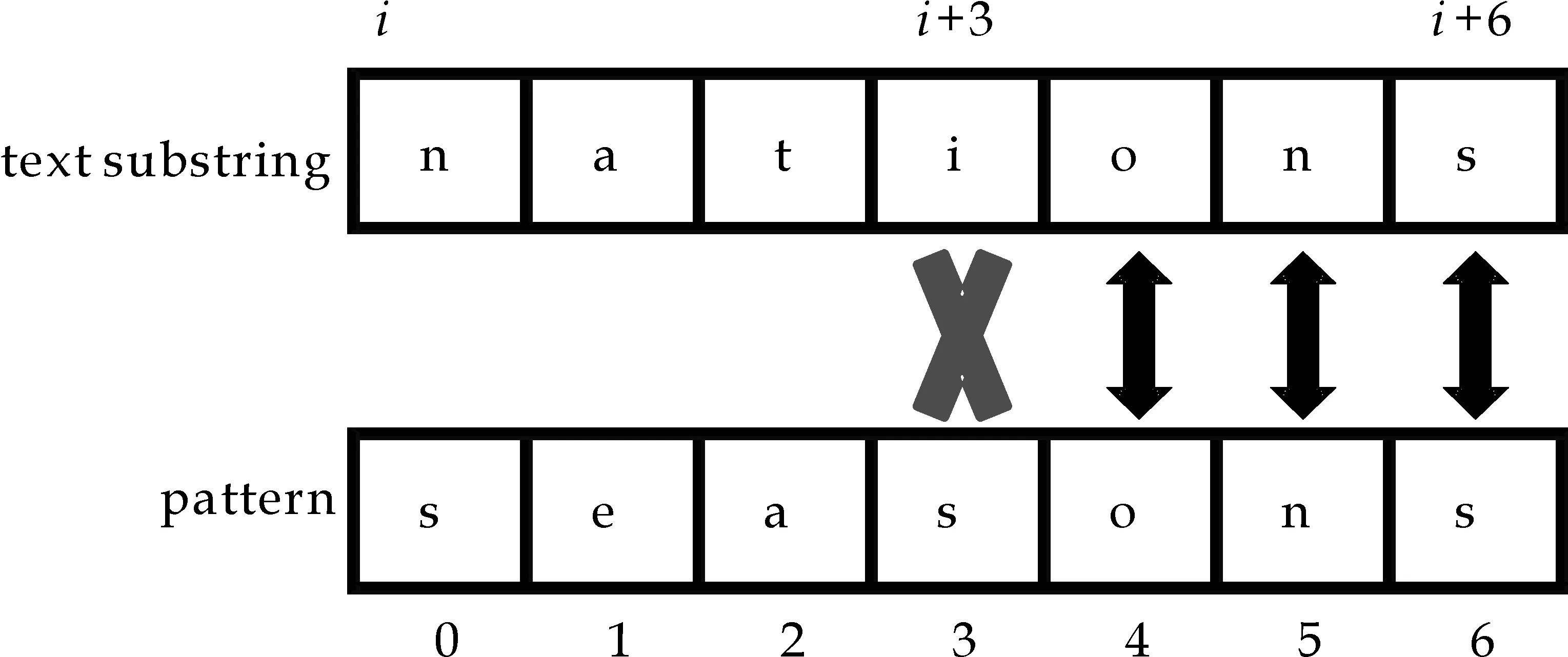
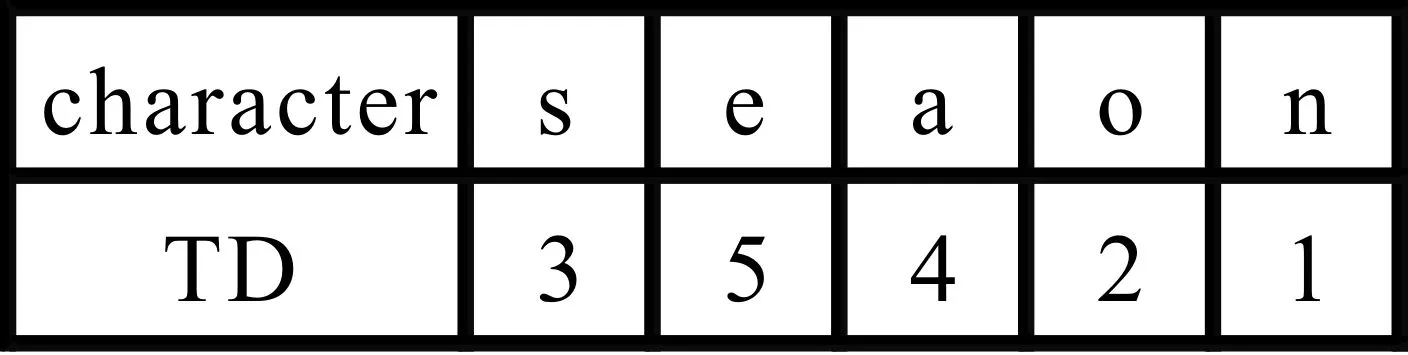
好后缀移动策略根据不匹配发生前匹配成功的部分(图1(a)中灰色的部分,也就是t[i+j+1]…t[i+m-1]=p[j+1]…p[m-1])来计算模式串的另一个移动量skip2[j].计算的依据是查看子串p[j+1]…p[m-1]与模式串p[0]…p[m-1]中的子串是否存在有完全匹配或者部分匹配的子串,例如存在p[j+1]…p[m-1]=p[g+1]…p[m-1+g-j]并且p[j]≠p[g](0≤g (a)字符p[j]和t[i+j]不匹配 (c)模式串移动量为j-k (d)模式串移动量为j-g (e)模式串移动量为m图1 BM算法工作原理图 当p[j]和t[i+j]不匹配时,即p[j]≠t[i+j],BM算法选择skip1[t[i+j]]和skip2[j]中的最大值作为模式串向前的移动量. 1.2 Horspool算法基本原理 Horspool算法是一种简化的BM算法,当不匹配发生时,Horspool仅利用BM算法中的坏字符移动策略计算模式串向前的移动量[3]. 如图2所示,当p[j]和t[i+j]发生不匹配时(如图2(a)所示),Horspool算法使用当前文本子串的最右边的字符t[i+m-1]作为坏字符,利用坏字符策略计算模式串的移动量.如果t[i+m-1]不出现在p[0]…p[m-2]中,可以将模式串向前移动至字符t[i+m-1]之后,移动量为skip[t[i+m-1]]=m,如图2(b)所示;反之,如果t[i+m-1]=p[k](0 ≤k (a)出现不匹配字符 (b)模式串移动量为m (c)模式串移动量为m-1-k图2 Horspool算法工作原理图 提高模式串匹配算法效率的有效方法之一是在不匹配发生后尽可能地加大模式串向前的移动量.如上所述,当发现p[j]和t[i+j]不匹配时,Horspool算法将t[i+m-1]用于坏字符移动策略来计算模式串的移动量,该移动量表示为skip[t[i+m-1]].但实际上,按照Horspool算法的思路,t[i+j+1]和t[i+m-2]之间的任何一个文本字符也都可以用于坏字符移动策略,在t[i+m-1]上获得的移动量并不一定是最大的. 例如,在图3所示的文本实例中,假设当前的文本子串是nations,模式串是seasons,其中模式串长度m=7.在下标3位置出现不匹配时,字符t[i+m-1]是s,即t[i+6]=s,用Horspool算法计算得到的移动距离是3,然而,如果用字符t[i+5],即字符n计算得到的移动距离是6,显然这个移动量比用Horspool算法计算得到的移动量大. 图3 用于解析本文算法基本原理的文本实例 为了获得尽可能大的移动量,在p[j]和t[i+j]不匹配时,将t[i+j+1]…t[i+m-1](也就是p[j+1]…p[m-1])之间的每一个字符t[i+k](也就是p[k])作为坏字符,用于坏字符移动策略计算出移动参考值Δ(k),然后从移动参考值Δ(j+1),…,Δ(m-1) 中选取最大值作为模式串的移动量,显而易见,skip[j]=max{Δ(j+1),…,Δ(m-1)},大于至少等于Horspool算法计算出的移动量skip[t[i+m-1]]. 还是图3的实例,在图4中给出了两种不同算法的预处理结果.图4(a)是Horspool算法的预处理结果,图4(b)是本文算法的预处理结果.从图4(a)可以看出,因为t[i+6]=s,不管在任何位置出现不匹配时,Horspool算法给出的模式串的移动量始终都等于TD(s),即就是3.而本文算法的移动量是和不匹配出现的位置有关,当在下标位置0到4任一位置出现不匹配时,模式串的移动量是6,当在下标位置5和6任一位置出现不匹配时,模式串的移动量是3.可见,本文算法的模式串移动量始终大于等于Horspool算法的模式串移动量. 根据模式串和BM算法的坏字符策略很容易实现本文算法的预处理部分.从右向左计算模式串的移动量,用skip[j](0 ≤j≤m-1)表示,其中skip[j](0 ≤j≤m-2)是用本文算法预处理计算得到,skip[m-1]等于Horspool算法的移动量skip[t[i+m-1]].在本文算法中分两步骤完成预处理,计算skip[j](0≤j≤m-2)值的计算分两步完成.首先,计算移动参考值Δ(j)(0≤j≤m-2),其中已知Δ(m-2)=TD(p(m-1))TD(p(m-1)表示用坏字符p(m-1)计算得到的移动量.用于计算参考值Δ(j)的模式子串是p[0]…p[j],坏字符是p[j+1],根据坏字符策略计算得到参考值Δ(j).假设k是满足p[j+1]=p[k]的最大值,其中0≤k≤j,那么Δ(j)=j+1-k.其次,基于参考值Δ(j)(0≤j≤m-2)计算移动量skip(j)(0≤j≤m-2).开始skip[m-2]被赋值为Δ(m-2),接下来计算其它skip[j]的值,每一个skip[j]的值都是选自Δ(j)和skip[j+1]中的最大值.例如,如果Δ(m-3)>skip[m-2],那么skip[m-3]=Δ(m-3),否则skip[m-3]=skip[m-2].显然,skip[j]是从Δ(j) 到Δ(m-2)中所有移动量的最大值. (b)本文算法的预处理结果图4 两种不同算法的预处理结果 (a)Horspool 算法的预处理结果 本文算法计算所有的 skip [ j ]( j =0,…, m -2)的预处理如下所示: /*第一步,计算Δ(j)*/ Δ(m-2)=TD[p[m-1]]; for(j=m-3;j >= 0;j--) for(i=j;i>=0;i-- ) if(p[i]==p[j+1]) Δ(j)=j+1-i; /*第二步,计算移动量skip[j]*/ skip[m-2]=Δ(m-2); for(j=m-3;j>=0;j--) if(Δ(j)>skip[j+1]) skip[j]=Δ(j); else skip[j]=skip[j+1]; 显然,根据模式串很容易计算每一个位置的移动量,实现预处理过程. 为了有效的比较本文算法和Horspool算法的效率,作者选用两种不同的文本对两种算法进行测试,这两种文本分别是:二进制文本和DNA(Deoxyribonucleic acid)序列,所有测试使用的源数据均下载自网站SMART ,其中二进制文本大小为5.0 MB,DNA序列大小为4.5 MB.实验所用的各种类型及不同长度的模式串均随机产生于以上的源数据.实验运行时间单位为毫秒. (1)实验1:测试文本为5.0 MB二进制文本,模式串的长度从3到10,20,30,40,50,60,70,80,90,100等共选取了18种,其中长度从3到7的模式串测试了0和1的所有组合情况,其他长度的模式串均随机从测试文本中选取了100个模式串用于实验,实验结果如图5所示.其中,图5(a)为模式串长度从3到10的测试结果,图5(b)为模式串长度为10,20直到100的测试结果.从图5(a)和图5(b)的匹配结果发现,几乎在所有匹配长度上,均提高了10 ms的匹配时间. (a)模式串长度为3-10 (b)模式串长度为10-100图5 两种算法在二进制文本上 平均运行时间比较 (2)实验2:测试文本为4.5 MB的DNA 序列,模式串长度的选取同实验2,其中模式串长度为3的模式串有64个,其它长度的100个模式串均从DNA序列中随机选取的,实验结果如图6所示.图6(a)是模式串长度从3到10的实验结果,图6(b)是其他模式串长度的实验结果.从图6(a)和6(b)来看,本文算法均比Horspool算法的效率高,但是模式串长度不同,效率提高的程度不同,图6(a)的结果显然没有图6(b)的提高效率程度高,所实现的效率与模式串长度成正比. (a)模式串长度为3-10 (b)模式串长度为10-100图6 两种算法在DNA序列上 的平均匹配时间 本文算法对基本模式串匹配算法BM的坏字符策略进行改进,实现了任一位置不匹配时,均有大于或等于同为坏字符策略实现匹配的Horspool算法的移动量.算法的基本思想简单、容易实现,在不同性质的实验数据上测试结果有效. 本文提出了一种有效的模式串匹配算法.当不匹配出现时,按照BM算法的坏字符策略计算当前已经匹配的每个字符的移动量为参考量,并从多个参考量中选择一个最大值作为模式串当前的移动量,任意位置的移动量均可以通过预处理计算得到.实验结果表明:在不匹配出现时,本文算法获得的模式串移动量总是最大的,从而有效地提高了模 式串的匹配效率.模式匹配算法已被广泛地应用于入侵检测和情报检索等系统中,并随着信息技术的不断发展,对于检索效率提出了更高的要求,高效率的匹配算法的提出具有极大的现实意义.本文作者的下一步工作将本文算法思想和其它模式串匹配技术相结合应用于病毒检测及DNA检测中. [1] 范洪博,姚念民.一种高速精确单模式串匹配算法[J].计算机研究与发展,2009,46(8):1 341-1 348. [2] R.Boyer,J.Moore.A fast string searching algorithm[J].Communications of the ACM,1977,20(10):762-772. [3] R.N.Horspool.Practical fast searching in strings[J].Software-Practice & Experience,1980,10(6):501-506. [4] M.Sunday.A very fast substring search algorithm[J].Communications of the ACM,1990,33(8):132-142. [5] Zhao X,Li S,Yang Y,et al.A new substring searching algorithm[J].Ieice Transactions on Information & Systems,2014,E97-D(7):1 893-1 896. [6] 胡金柱,熊春秀,舒江波,等.一种改进的字符串模式匹配算法[J].模式识别与人工智能,2010,23(1):103-106. [7] 李明月,张善卿,陆剑锋,等. 一种改进的Sunday匹配算法[J].杭州电子科技大学学报,2015,35(1):93-96. [8] 韩光辉,曾 诚.Boyer-Moore串匹配算法的改进[j].计算机应用,2014,34(3):865-868. [9] Sun Kelei.Fast algorithm for pattern matching in intrusion detection system[J].Journal of Anhui University of Science and Technology (Natural Science),2006,26(3):52-55. [10] G.Navarro,M.Raffinot.Flexible pattern matching in strings[M].Cambridge:Cambridge University Press,2002:19-22. 【责任编辑:蒋亚儒】 An efficient pattern matching algorithm for string searching ZHAO Xiao1, HE Li-feng1, WANG xin1, YAO Bin1,CHAO Yu-yan2, WANG Ya-ni1 (1.College of Electrical and Information Engineering, Shaanxi University of Science & Technology, Xi′an 710021, China; 2.Faculty of Environment, Information and Business, Nagoya Sangyo University, Aichi 488-8711, Japan) According to the analysis of the famous BM algorithm and the Horspool algorithm,we propose a simple and efficient pattern matching algorithm for string searching.When a mismatch happens,for shifting the pattern to the right,the shift amount in the Horspool algorithm is computed by using the rightmost character of the current text substring to the bad-character strategy.In comparison,the shift amount of our algorithm is the maximum one among all the shift amounts computed by using each of the already-matched characters.The maximum shift amount for each mismatch position of the pattern can be pre-computed by using the pattern only.Experimental results demonstrated that our algorithm can obtain a larger shift amount for a mismatch,and thus enhanced the efficiency of pattern matching for string searching. pattern matching; string searching; BM algorithm; Horspool algorithm 2016-09-19 国家自然科学基金项目(61601271,61471227,61603234); 陕西省科技厅科技计划项目(2016SF-444); 陕西省教育厅自然科学专项科研计划项目(16JK1087) 赵 晓(1978-),女,陕西西安人,讲师,在读博士研究生,研究方向:模式识别 1000-5811(2017)01-0183-05 TP393.0 A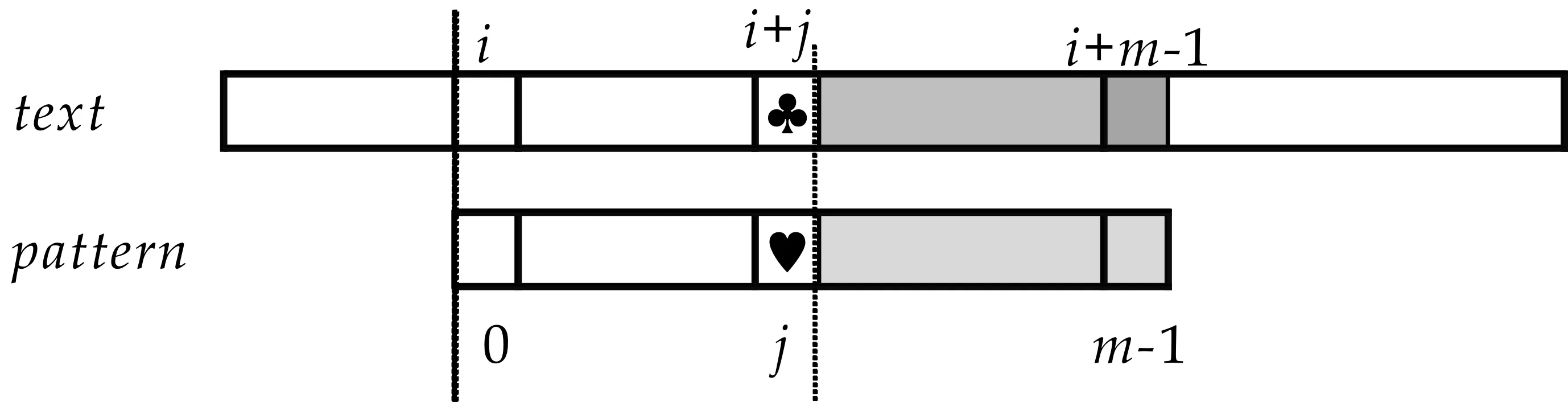

2 本文算法的基本原理

3 实验结果

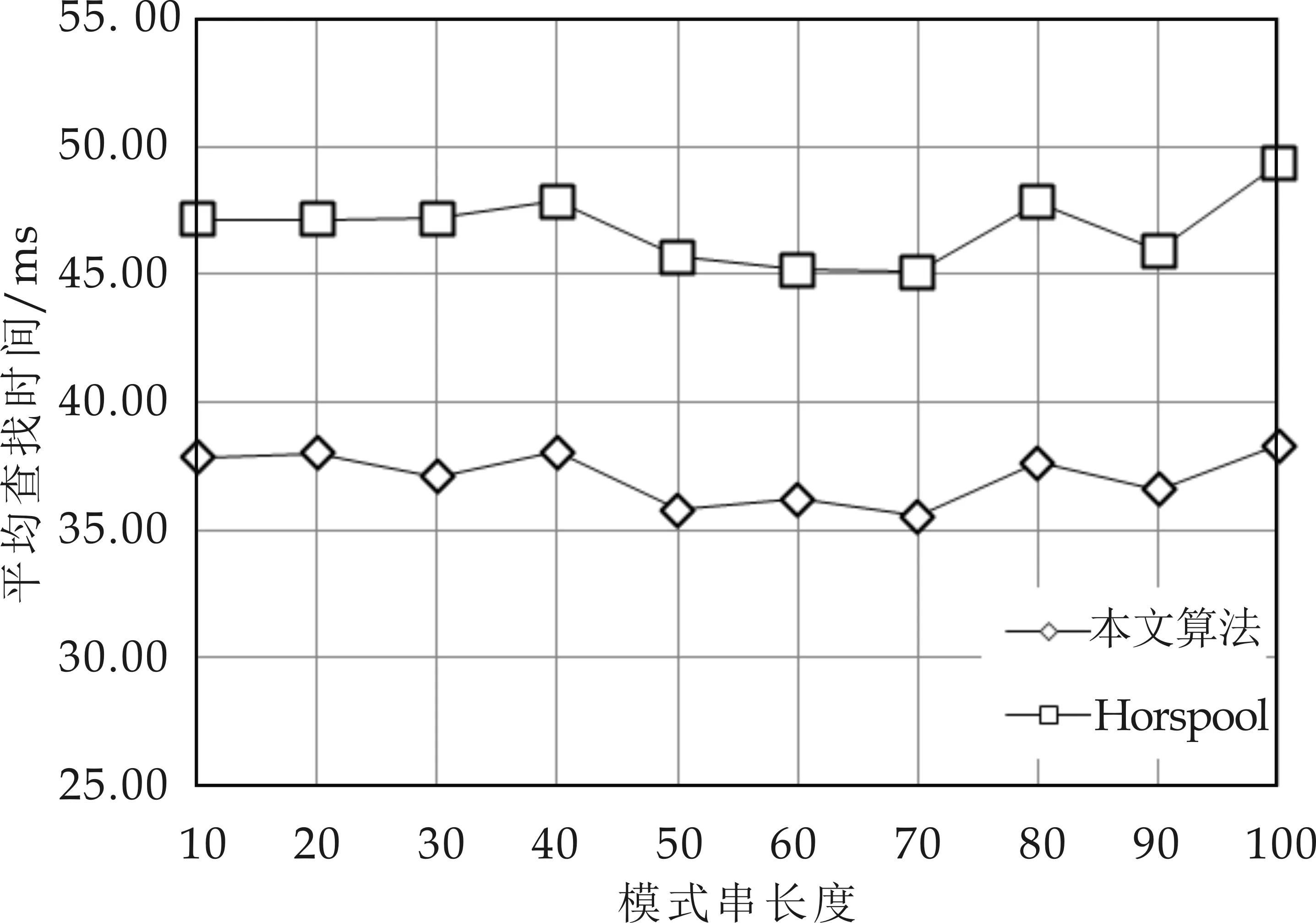
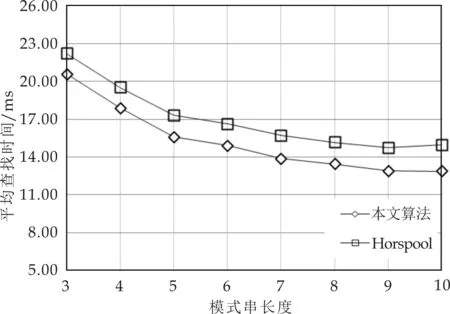
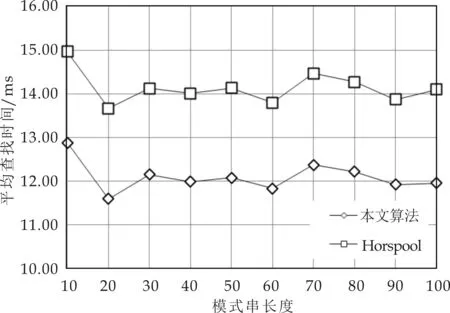
4 结论

