基于贝叶斯网络的雷达装备维修质量评价
王 敏,杨江平,王永攀,洪 进,刘维建
(空军预警学院,湖北 武汉 430019)
基于贝叶斯网络的雷达装备维修质量评价
王 敏,杨江平,王永攀,洪 进,刘维建
(空军预警学院,湖北 武汉 430019)
针对当前装备维修质量评价忽视维修过程影响因素这一问题,将过程评价指标体系作为修后评价指标体系的先验知识,构建了一种基于贝叶斯网络的雷达装备维修质量评价模型。首先,建立了过程评价指标体系和修后评价指标体系,并对各项指标进行了简要分析。然后,建立了维修质量评价的贝叶斯网络模型,通过改进的模糊综合评价方法确定了根节点的先验概率,通过专家经验法确定了子节点的条件概率,并给出了模型的详细求解过程。最后,通过仿真实验对所提方法进行验证。结果表明,该方法能够在一定程度上解决雷达装备的维修质量评价问题,为完善雷达装备的维修质量评价理论提供了有效途径。
雷达装备;维修质量评价;贝叶斯;熵权;模糊综合评价
维修质量(maintenance quality,MQ)评价是提高装备维修质量和维修效率的重要途径[1],也为装备作战效能发挥提供重要的保障依据。近年来,围绕装备维修质量评价的报道较多,涉及飞机、导弹、工程机械等多个装备领域[2-4]。现有文献主要集中在对装备修复后维修质量评价(简称修后评价)指标体系和评价方法,很少考虑影响装备维修质量的维修过程因素,而维修过程因素作为影响维修质量的关键因素,其作用不容忽视。为此,部分学者开始对装备维修过程中的维修质量评价(简称过程评价)进行研究,取得了一些研究成果[5-7]。这些研究虽然对过程评价进行了一定的分析,但是忽视了修后评价,因此,装备维修质量的评价理论尚不完善。为了更加科学地对装备的维修质量进行综合评价,人们开始考虑将修后评价和过程评价结合起来对装备的维修质量进行综合评价[8]。但是,现有研究主要将两种情况得到的评价结果进行综合考虑,并未提出将二者进行有机结合[9]。由于过程评价指标对修后评价指标影响较大、关联性强,并且考虑到指标体系构建的独立性原则,过程评价指标和修后评价指标不能在同一个评价指标体系中共存。为此,如何将过程评价和修后评价有机结合起来,已成为装备维修质量评价工作面临的一个难题。
考虑到过程评价指标对修后评价指标的影响,笔者提出将过程评价指标体系作为修后评价指标体系的一个先验知识,通过贝叶斯网络模型对装备维修质量进行综合评价的观点。为此,以雷达装备为例,首先对影响装备维修质量的过程指标和修后指标进行了选取与分析;然后,建立了雷达装备维修质量评价的贝叶斯网络模型;最后,以某型雷达为例,通过仿真分析对构建的模型进行了验证。
1 维修质量评价指标分析
1.1 指标选取原则
评价指标的选取直接影响到装备维修质量的评价结果,为保证评价结果的真实、有效,在选取评价指标时应遵循以下原则:①从指标的角度来讲,选取的指标应该具备系统性、客观性、完备性、独立性和时效性;②从系统的角度来讲,指标的选取应遵循管理持续改进,最大限度地保留系统性能和提高效费比;③从评价的角度来讲,对指定时间内因装备维修质量问题引起等级事故、严重影响作战任务完成或因性能指标严重恶化而导致装备不能按要求完成任务保障,实行一票否决制。
1.2 评价指标选取与分析
1.2.1 过程评价指标
过程评价指标主要从影响装备维修过程的因素中选取。目前,以“5M1E”(即:人、机、料、法、检、环)为主的维修质量影响因素已经得到人们的认可,对各项指标含义的分析也比较全面[10]。因此,笔者在此基础上构建过程评价指标体系,如图1所示。
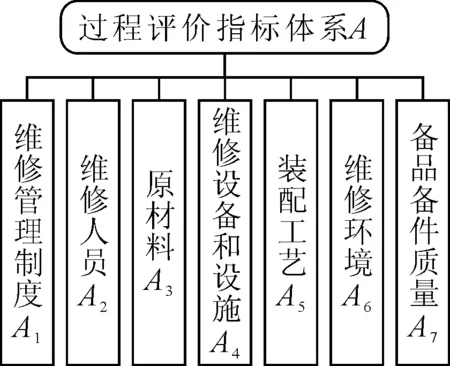
图1 过程评价指标体系
1.2.2 修后评价指标
由于雷达装备组成系统较多,涉及到的影响因素复杂多样。为简化评价指标体系,最大限度地反映装备的维修质量状况,笔者分技术状况、各分系统维修情况、一次维修费用合理值、保障性与安全性恢复程度、维修管理质量影响度5个一级指标建立了雷达装备的修后评价指标体系,具体如图2所示。
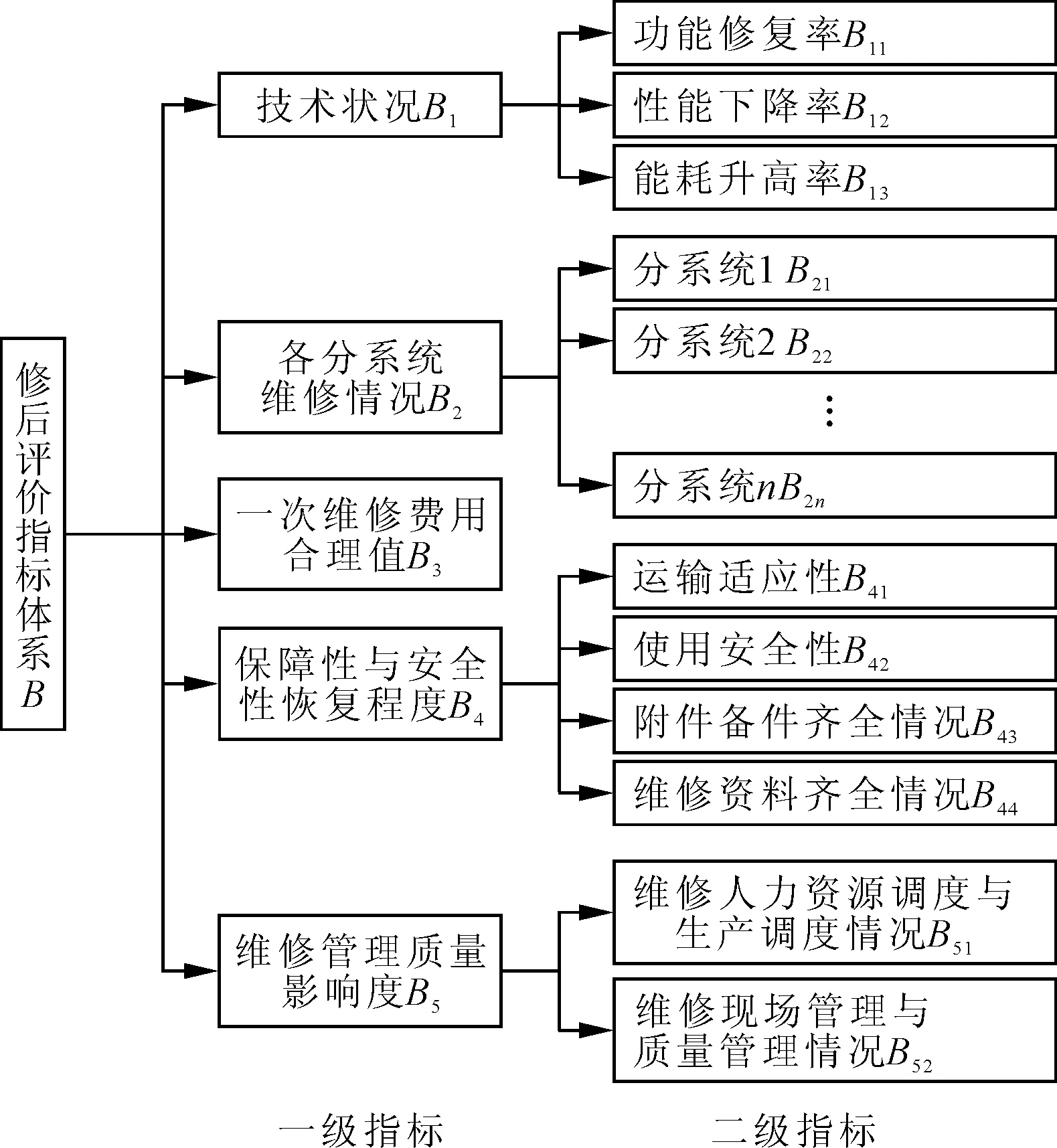
图2 修后评价指标体系
(1)技术状况。技术状况直接表征装备的性能技术状态,包括功能恢复率GL、性能下降率SL和能耗升高率gL3个二级指标。
功能恢复率GL是指在规定的技术条件下,装备的功能恢复程度,是维修质量的基本度量。该指标主要通过检查得到,属于定性指标。其计算公式为:
GL=WJT/WJZ
(1)
式中:WJT为装备检查项目合格数;WJZ为检查项目总数。
性能下降率SL是指在规定的技术条件下,装备性能指标下降的程度,是维修质量的重要度量。该指标主要通过测试得到,属于定量指标。其计算公式为:
(2)
式中:n为测试性能指标数目;ωi为性能指标i的权重;Si为性能指标i的标准值;SiD为性能指标i的测试值。
能耗升高率gL是指在规定的技术条件下,装备能耗指标的升高程度,是维修质量的重要度量。该指标主要通过测试得到,属于定量指标。其计算公式为:
(3)
式中:n为测试能耗指标数目;ωi为能耗指标i的权重;gi为能耗指标i的标准值;giD为能耗指标i的测试值。
(2)各分系统的维修情况。即指在装备维修工作完成后,装备的润滑、紧固、调整、清洁等工作的完成情况,主要通过目视检查的手段进行,属于定性指标。其二级指标主要由各分系统维护保养情况组成,第i个分系统评价分数的计算方法为:
(4)
式中:Scorei为第i个分系统最终评价分数;Scoreij为第i个分系统中第j个评定点扣除的分值。
(3)一次性维修费用合理值。在进行装备维修时,需同时考虑维修费用因素,其是衡量维修质量的一个重要因素。维修费用通常用维修费用合理程度来衡量,具体计算方法见文献[11]。
(4)保障性与安全性恢复程度。根据GJB 4386-2002《武器装备维修质量评定要求和方法》的内容,保障性与安全性恢复程度是衡量维修质量的一个重要因素。其可分为4个指标,分别为运输适应性、使用安全性、附件备件齐全情况与维修资料齐全情况。各项指标均通过专家打分的方法进行计算,具体计算方法可参考“各分系统维修情况”的二级指标。
(5)维修管理质量影响度。开展装备维修质量评价的根本目的在于通过评价发现装备维修中存在的问题,进而通过整改,可以避免下次维修中类似问题的发生,最终提高装备的维修质量。维修人力资源调度与生产调度情况包括人员差错情况和生产调度影响度情况两个评定点,每个评定点50分;维修现场管理与质量管理情况包括现场管理影响度与质量管理影响度两个评定点,每个评定点50分。评定时,每个评定项目100分,采取扣分制得到二级指标的最终得分。
2 维修质量评价模型
2.1 贝叶斯网络
贝叶斯网络[12]于20世纪80年代提出,主要通过概率理论与统计分析,解决不确定性因素的表述以及推理问题。贝叶斯网络是一个有向无环图,通常由两部分组成,即网络结构和变量的概率分布。一个具有N个节点的贝叶斯网络可以用N=<
P(Vi|Pa(Vi),A(Vi))=P(Vi|Pa(Vi)) (5) 当根节点的条件概率确定时,根据条件独立的假设调节,可计算得到包含所有节点的联合概率分布,即:
P(Vi)=P(V1,V2,…,VN)=
(6)
通过对构建的指标体系及装备的维修流程进行分析,可以发现:①所选取的过程评价指标直接影响的是装备的维修工作质量(maintenance work quality, MWQ);②MWQ通过影响修后评价指标体系中的技术状况B1、各分系统维修情况B2和一次维修费用合理值B33个一级指标来间接影响装备的维修质量;③指标B1和B2通过影响装备的维修性能(maintenance performance, MP)来影响装备的维修质量;④保障性与安全性恢复程度B4和维修管理质量影响度B5属于装备维修质量管理(maintenance quality management, QM)的范畴,装备的维修质量管理情况也是影响装备维修质量的一个重要指标。为此,笔者根据各指标对装备维修质量影响的因果关系,构建出如图3所示的贝叶斯网络模型。
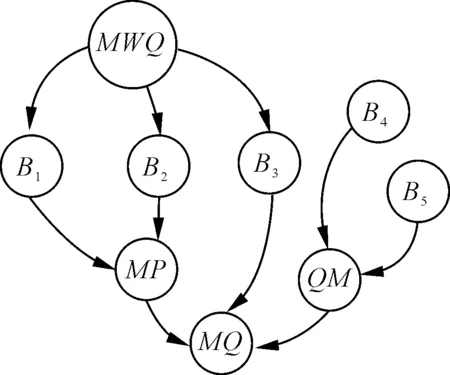
图3 贝叶斯网络模型
通过分析所建立的贝叶斯网络模型,并结合贝叶斯网络理论知识,得到维修质量MQ的联合概率PMQ为:
PMQ=P(MQ|MP,B3,QM)·P(MWQ)·
P(MP|B1,B2)·P(B1|MWQ)·
P(B2|MWQ)·P(B3|MWQ)·
P(QM|B4,B5)·P(B4)·P(B5)
(7)
2.2 贝叶斯网络关键参数求解
根据贝叶斯网络理论可知,求解贝叶斯网络的关键在于求解根节点的先验概率和确定贝叶斯网络的条件概率。结合建立的维修质量评价指标体系可发现,在构建的贝叶斯网络模型中,根节点MWQ、B4和B5都包含有独立的子评价指标体系,为此,笔者采用模糊综合评价法确定根节点的先验概率。长期以来,贝叶斯网络条件概率的确定是一个难题,往往通过人为经验确定或者根据统计试验数据估计得到。考虑到雷达装备试验数据较少,笔者采用专家经验法确定贝叶斯网络的条件概率分布表(CPT)。
2.2.1 基于改进模糊综合评价法的先验概率确定
模糊综合评价法[13]是利用模糊集理论进行评估的一种方法,可将不确定因素及其模糊性因素量化,因此,评估结果更合理、更客观。对于常规模糊综合评价方法而言,往往用隶属度来描述模糊集合。然而,常用的隶属函数为确定性的隶属函数,包括三角形函数、梯形函数、线性隶属函数等,其很难体现出评价结果的随机性、模糊性与不确定性。云模型理论可描述某些定性概念与相应数值表示之间的不确定性转换量,可较好地量化出定性语言的模糊性和随机性。通常,可用(Ex,En,Ee)表示云的数字特征,其中,Ex表示期望,表征模糊信息的中心值;En表示熵,表征定性概念的模糊度;Ee表示超熵,表征熵的离散程度。
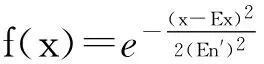
得到云模型的隶属度后,则可通过改进模糊综合评价方法来确定根节点先验概率,其计算步骤如下:
(1)确定评价因素集U={U1,U2,…,Um}。其中,Ui(i=1,2,…,m)表示影响评价对象的各种指标。
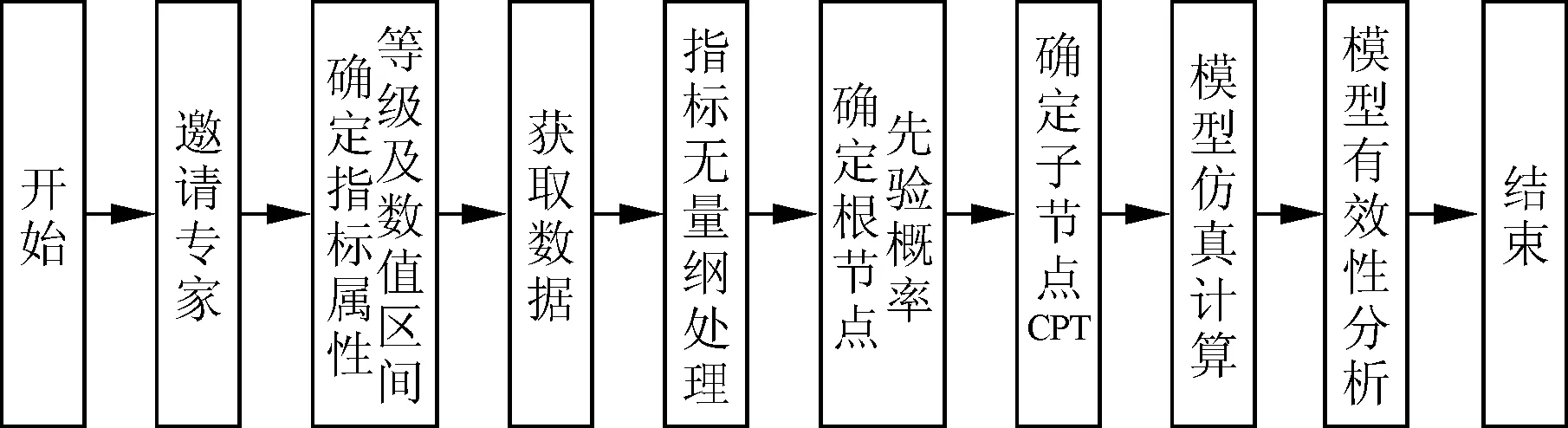
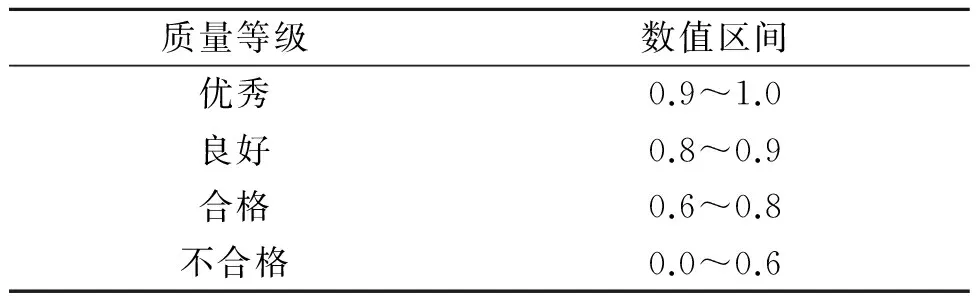
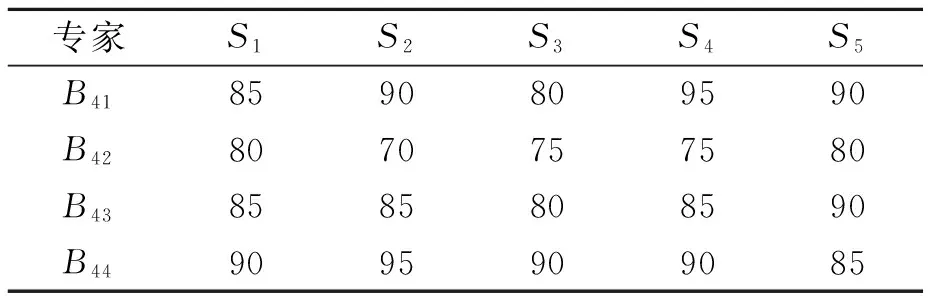
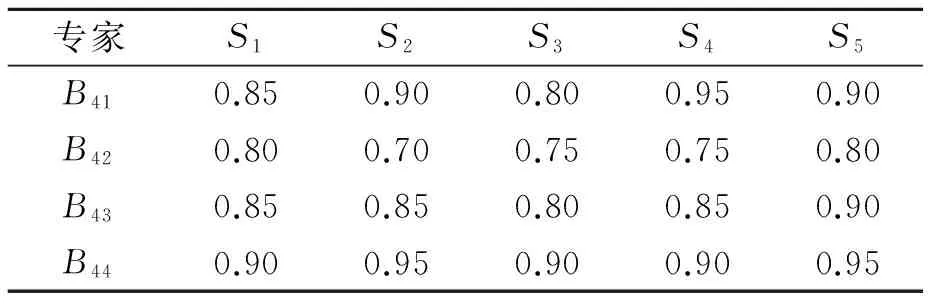
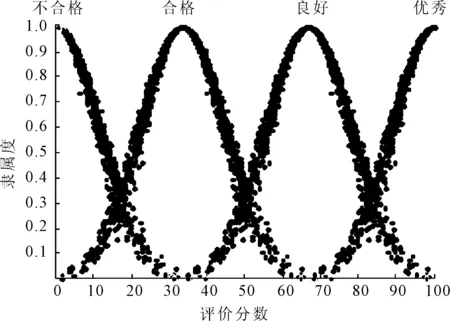
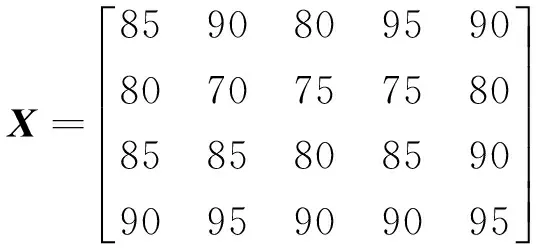
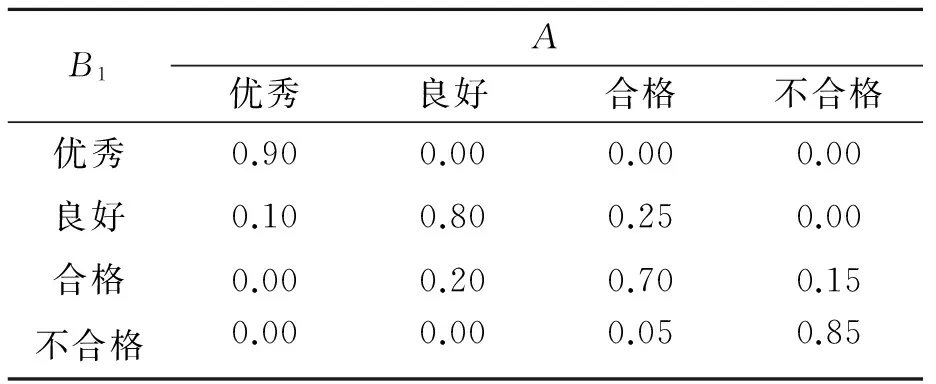
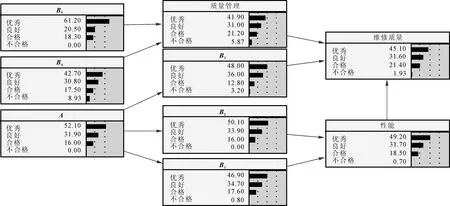
(2)确定评价集V={V1,V2,…,Vn},并给定对应的决策值C={c1,c2, …,cn},其中,n为评判等级的个数;Vj(j=1,2,…,n)为各评价等级的评语;cj为评判等级隶属云所对应的分值,并且c1 (3)确定指标权重W={w1,w2,…,wm}。笔者利用熵权法[14]确定指标权重,首先对指标数据进行无量纲处理可得到: (9) 则第i个评价指标的熵为: (10) (11) 第i个指标的熵权即权重为: (12) (4)构建隶属度权重矩阵R,其表示评估指标属于不同评判等级的程度。当有p个专家对m个指标打分时,可构造相应的评价值矩阵X=(xai)p×m,其中,xai表示由第a个专家给出的对第i个指标的分数。用δid表示第i个指标属于第d个评判等级的隶属度,则有: (13) 式中:Exd为第d个评判等级对应的决策值。因此,第i个指标隶属于第d个等级的隶属度权重可表示为: (14) 其中,d=1,2,…,s。则m个指标的隶属度权重矩阵R为: (15) 其中,rij为因素集中因素Ui对应评价集中等级Vj的隶属关系。 (5)确定先验概率。根据求得的指标权重,得到模糊综合评价向量B为: B=W·R=(b1,b2,…,bs) (16) 其中,bd(d=1,2,…,s)为评估结果隶属于评价集Vj的隶属度,即为先验概率。 2.2.2 基于专家经验法的条件概率确定 贝叶斯网络的条件概率可由专家根据经验直接给出,为说明问题,以节点A与节点B1为例建立条件概率分布表(CPT),如表1所示。其中,每一列的概率总和为1。同理,可得到其他节点的CPT。 表1 节点A与节点B1的CPT范例 为了验证提出的维修质量评价方法的可行性与有效性,利用上述方法对某型雷达的维修质量进行评估。为进一步指导维修质量评价工作的有序开展,给出的评价实施步骤如图4所示。 图4 评价实施步骤 (1)邀请专家。某型雷达装备的研用结合、技术复杂等特点,增加了雷达维修质量评价工作的难度。所建立的评价指标体系多为定性指标,各项指标的量化均通过专家打分法获得,因此,在评价工作开始前,需要邀请一定数量的专家参与。考虑到维修质量评价工作实施的便捷性与可操作,现邀请5位业内专家组成评价组,评价组成员如表2所示。为了说明问题,邀请专业权威较高的5位专家对某型雷达的维修质量评价进行相关的评定。以节点B4为例说明根节点先验概率的确定方法。 表2 评价组成员 (2)确定指标属性等级及数值区间。首先将雷达各指标的属性等级分为优秀、良好、合格、不合格4个等级,依据专家经验,对各项指标质量等级的数值区间进行设定,得到如表3所示的指标质量等级状态表。 表3 指标质量等级状态表 (3)获取数据。该数据是指贝叶斯网络根节点对应的子指标数据。笔者构建的贝叶斯网络模型,包含B4(保障性与安全性恢复程度)、B5(维修质量管理影响度)和MWQ(维修工作质量)3个根节点,每个根节点包含各自的子指标体系,如B4包含B41(运输适应性)、B42(使用安全性)、B43(附件备件齐全情况)、B44(维修资料齐全情况)4个子指标。为了说明情况,给出子指标B41~B44的数据,如表4所示。 表4 子指标B41~B44数据 (4)指标无量纲处理。由于评价指标体系中同时存在定量指标与定性指标,且各项指标的单位不尽相同,为统一量纲,需对获取的数据进行无量纲处理。对于定量指标,在指标获取时已进行了无量纲处理;对于定性指标,由于各项指标的成绩评定采用百分制,因此,可通过指标值除以100分的方法对定性指标进行无量纲处理。为说明情况,以子指标B41~B44无量纲处理为例,给出了最终的无量纲指标值,如表5所示。 表5 子指标B41~B44无量纲指标值 (5)确定根节点先验概率。由于指标众多,为说明问题,以根节点B4为例说明根节点先验概率的确定方法。①确定评价因素集U={B41,B42,B43,B44}。②确定评价集V={优秀,良好,合格,不合格}和决策值集C={100,100/3,50/3,0}。③借助熵权法求取指标权重。根据表5所示的无量纲指标值,得到指标值的无量纲矩阵D=(dij)m×n,如式(17)所示,则各评价指标的熵为H={0.999 0,0.999 2, 0.999 6,0.999 8};进一步可求得指标B41~B44的权重向量W={0.427 2,0.308 4,0.175 1,0.089 3}。④构建隶属度权重矩阵R。首先,根据决策值集C={100,50/3,100/3,0},进一步可得到各评价集对应云模型的期望值为Exd= {Ex1,Ex2,Ex3,Ex4}={100,200/3,100/3,0},熵为En′=100/9,评价集的隶属云标尺如图5所示。然后根据表4获得的子指标B41~B44数据,构建评价指标的评价值矩阵X,进一步可求得指标B41~B44的隶属度权重矩阵R,分别如式(18)和式(19)所示。⑤根据求得的指标权重,得到节点B4的先验概率为P(B4)={0.427 2,0.308 4,0.175 1,0.089 3}。同理,可求得节点A先验概率为P(A)={0.520 8,0.319 0,0.160 2,0.000 0},节点B5先验概率为P(B5)={0.612 4,0.205 1, 0.182 5,0.000 0}。 图5 评价集的隶属云 (17) (18) (19) (6)确定子节点条件CPT。结合雷达维修质量评价实际情况以及各指标对维修质量的影响情况,由评价组专家根据经验制定贝叶斯网络的CPT。由于贝叶斯网络中节点众多,为说明问题,对于以节点A与节点B1为例建立CPT如表6所示。 表6 节点A与节点B1的CPT (7)模型仿真计算。NETICA是专门用来研究贝叶斯网络的一款性能优良、高效、便捷的软件,在解决贝叶斯网络的推理问题方面功能全面,应用性强,已在多个领域得到广泛应用。为简化运算、提高模型的便捷性与实用性,笔者利用NETICA软件来实现模型的计算,并对雷达装备维修质量的贝叶斯网络模型进行建模仿真,输入贝叶斯网络的先验概率和CPT,仿真得到的结果如图6所示。 图6 贝叶斯网络仿真图 从图6可看出维修质量评价结果隶属于各评价集的概率(取四舍五入)为:优秀的概率为0.451 0,良好的概率为0.316 0,合格的概率为0.214 0,不合格的概率为0.019 3。通过综合分析评价结果得知,该型装备此次的维修质量为优秀。 (8)模型有效性分析。模型的有效性是模型可用性的度量,对模型的有效性进行分析可以检验模型是否真实、可行。为此,笔者采用定性分析的方法对两种极端条件下的贝叶斯网络模型进行了仿真,仿真结果如表7所示。 由表7可知,保持维修质量管理指标B4、B5状态不变,设定维修工作质量MWQ为不合格时,则装备的维修质量评定为不合格;保持MWQ不变,当B4、B5同时不合格时,装备的维修质量并未评定为不合格,其综合评定结果为合格。通过进一步分析,可得出如下结论:①维修工作质量是整个装备维修工作过程中的关键因素,当维修质量不合格时,装备维修质量一定不合格;②而当维修工作质量优秀时,其维修工作质量并不一定为优秀。这个结论与部队当前装备的维修质量状态相一致,也从侧面验证了维修质量评价模型的有效性。 雷达装备的维修质量评价问题已成为装备使用方亟需解决的难点问题。为此,笔者提出了一种基于贝叶斯网络的雷达装备维修质量评价方法。主要开展了以下工作:①构建了雷达装备的过程评价指标体系和修后评价指标体系,解决了维修质量评价指标的选择问题;②提出一种基于贝叶斯网络的维修质量评价方法。该方法将过程评价指标体系作为修后评价指标体系的先验知识,对二者进行了有机的融合。同时,给出了具体的模型构建及求解步骤;③以某型雷达维修质量评价为例,对模型进行了仿真。通过模型敏感度分析,验证了提出的模型的可行性与有效性,为提高装备的维修质量提供了理论依据。 [1] 李永杰,肖斌,汪厚祥.装备维修保障信息共享与集成应用的实现[J].武汉理工大学学报(信息与管理工程版),2011,33(3):443-463. [2] 梁新,刘宝平,李凛然.大型武器装备系统成熟度评估及优化[J].武汉理工大学学报(信息与管理工程版),2015,37(3):344-348. [3] WANG J, WANG Y F, DAI L, et al. Dynamic evaluation model and application methods for engineering machine maintenance quality[J]. International Journal of Plant Engineering and Management, 2012,17(1):50-57. [4] 郑建华,黎放,狄鹏,等.海军武器装备体系作战能力评估模型研究[J].武汉理工大学学报(信息与管理工程版),2009,31(2):314-317. [5] 段林杰,扈延光.装备维修过程质量评估研究[J].价值工程,2012,31(22):38-40. [6] 石连玉,魏军.舰船装备维修过程质量评估研究[J].舰船电子工程,2009,29(8):170-172. [7] 黄建新,边亚琴.新型武器装备维修质量综合评估模型研究[J].航空维修与工程,2009(5):48-50. [8] 孙华昕,梁工谦,程培培.装备维修质量指标评价及质量改进模型研究[J].大型铸锻件,2005(1):39-43. [9] FU Y. Analysis of influencing factors to the maintenance quality of the aviation equipment based on interpretative structural modeling[C]∥Proceedings of 2011 International Conference on Grey Systems and Intelligent Services. Nanjing: IEEE,2011:748-752. [10] 刘颖,曹玉坤,郭金茂,等.影响武器装备维修质量的基本要素分析[J].装甲兵工程学院学报,2001,15(3):28-32. [11] CHEN W, NIU Y. Open press electrical accident risk assessment based on Bayesian network [J]. Procedia Engineering, 2012(43):542-546. [12] 熊盛武,史旻,刘麟,等.基于贝叶斯网络的并行分布估计算法研究[J].武汉理工大学学报(信息与管理工程版),2005,27(2):19-21. [13] CHEN J F, HSIEH H N, DO Q H. Evaluating teaching performance based on fuzzy AHP and comprehensive evaluation approach [J]. Applied Soft Computing, 2015(28):100-108. [14] YAN J, FENG C, LI L. Sustainability assessment of machining process based on extension theory and entropy weight approach [J]. The International Journal of Advanced Manufacturing Technology, 2014,71(5-8):1419-1431. WANG Min:Doctorial Candidate;Air Force Early Warning Academy,Wuhan 430019, China. Assessment of Maintenance Quality of Radar Equipment Based on Bayesian Network WANGMin,YANGJiangping,WANGYongpan,HONGJin,LIUWeijian The influence factors in repair process are usually ignored in maintenance quality assessment. This paper proposed a maintenance quality assessment method for radar equipment, based on Bayesian network by taking the procedural indicator system as a prior knowledge of the repaired indicator system. Firstly, the procedural and repaired indicator systems are built and simple analysis of the indexes is given. Secondly, a maintenance quality assessment model based on Bayesian network is established, and the prior probability and conditional probability are also confirmed by improved fuzzy comprehensive evaluation method and expert experience method, respectively. Finally, simulations and analysis of one instance are given to verify the effectiveness of the proposed method. Results show that the proposed method can solve the problem of maintenance quality assessment for radar electronic equipment to a certain extent, and hence it can serve as a theoretical reference to improve the maintenance quality assessment theory. radar equipment; maintenance quality assessment; Bayesian network; entropy weight; fuzzy comprehensive evaluation. 2095-3852(2016)06-0700-08 A 2016-07-18. 国家部委基金项目(KJ2014023200B11145);博士研究生专项课题基金项目(2014JY546). TN95;E264 10.3963/j.issn.2095-3852.2016.06.013 收稿日期:王敏(1987-),女,湖北武汉人,空军预警学院博士研究生.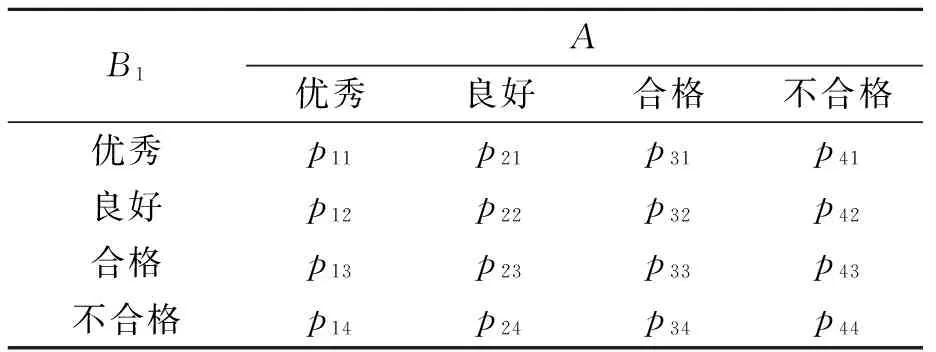
3 算例仿真与分析



4 结论

