大规模风电场群逐级汇聚演化分析

赵 姝,崔田丽

(1.东北电力大学 电气工程学院,吉林 吉林 132012; 2.国网山东省电力公司烟台市福山区供电公司,山东 烟台 264000)

大规模风电场群逐级汇聚演化分析

赵 姝1,崔田丽2

(1.东北电力大学 电气工程学院,吉林 吉林 132012; 2.国网山东省电力公司烟台市福山区供电公司,山东 烟台 264000)

针对大规模风电场群数据缺失影响整个风电场群输出功率的问题,笔者根据宁夏地区大规模风电场群地理数据和功率数据,阐述了持续功率曲线描述的风电功率特性以及研究风电场地理分布对大规模风电场群汇聚效应的影响,分析了持续功率曲线在风电场分布影响因素下的演变规律,提出了根据地理关联度分级汇聚研究大规模风电场群的方法。实践证明,大规模风电场群逐级汇聚演化分析方法能够解决大规模风电规划、功率预测等实际工程数据缺失的问题。

大规模风电场群;汇聚效应;持续功率曲线;风电场地理分布

目前,大型风电机组的输出功率是随机变动的,不具有电能存储的功能,给风电并网带来了能源规划、预测等问题[1]。为了从机理上解决风电并网问题,多数学者从风电功率波动性模型的建立入手,归纳为概率密度函数法[2-4]和随机序列法[5-8]。文献[9-10]建立了风场出力相关系数与风场距离之间的指数模型,初步探讨了地理位置和风电出力的关系。文献[11]考虑了同一电力系统中的多个风电场之间固有的空间相关性对风电功率波动性的影响,作为探讨空间相关性与风电汇聚关联的基础。由于以上文献实际场景风电场地理数据的缺失,建立的模型以及分析方法还局限于单独风电场等较小范围或仿真层面,没有对大规模风电场群分层逐级汇聚,探究其演化规律,不能很好地切合大规模风电场群场景,因此本文阐述了持续功率曲线在描述大规模风电场群总输出功率的突出优势,将风电场输出功率按由大到小的顺序排列,以实际工程提供的大规模风电场群数据为依据划分风电场群,逐级汇聚,并用MATLAB编程画出汇聚后的持续功率曲线,分析其演化规律与风电场地理分布以及装机容量的联系,消除了风电场分布对整个风电场群输出功率的影响。

1 大规模风电场群实测数据的处理

1.1 风电场地理数据的处理

工程提供的地理数据是根据各风电机组地点经纬度,取各风机经纬度中间值作为风电场的地理位置。由于地球是一个球体,不同经纬度每度对应的地理长度不同,因此要设定一个参考点,应将三维地理转化为二维地理关系,如图1所示,其数学模型如下:

(1)

式中:x、y为风电场对应的经纬度;x0、y0为参考点经纬度;Δx、Δy分别为距离参考的点横向距离和纵向距离,km;a(x)、b(y)为某固定纬度下每经度对应长度,此数据查表获得,km。

图1 三维转二维示意图

1.2 风电场功率数据的预处理

1.2.1 功率数据的容许误差

功率数据的采集及传输过程并非静止无干扰,采集设备也有故障,数据具有误差是必然的,通过实测数据进行功率分析前有必要对数据进行合理性检验和修正。理论上,风电场输出功率应在0到额定功率之间;在实际工程中,允许风电功率在0附近有波动,甚至有时会出现略小于0的负值情况。假设最大容许误差为5%,实际应用中风电场输出功率标幺值的容许区间为[-0.05,1.05],对容许范围内的功率数据进行保留。

2.2.2 病态功率数据预处理

通过对功率数据的整理,发现允许范围外的三类病态数据。

第一类:超过额定功率5%(按额定功率5%处理);第二类:低于额定功率-5%(按额定功率-5%处理);第三类:断档0值(工程记录等意外事故造成断档数据不全,需要数据补档。采用相同时段相邻两日的数据平均值作为其补档数据)。

对某大规模风电场群内风电场每5 min测录1次,共1 a时间的即时功率数据。根据《国家电网公司风电场接入电网技术规定(修订版)》中对风电场10 min和1 min最大功率变化量进行的规定,利用线性插值公式计可算出5 min最大功率变化量,如表1所示。

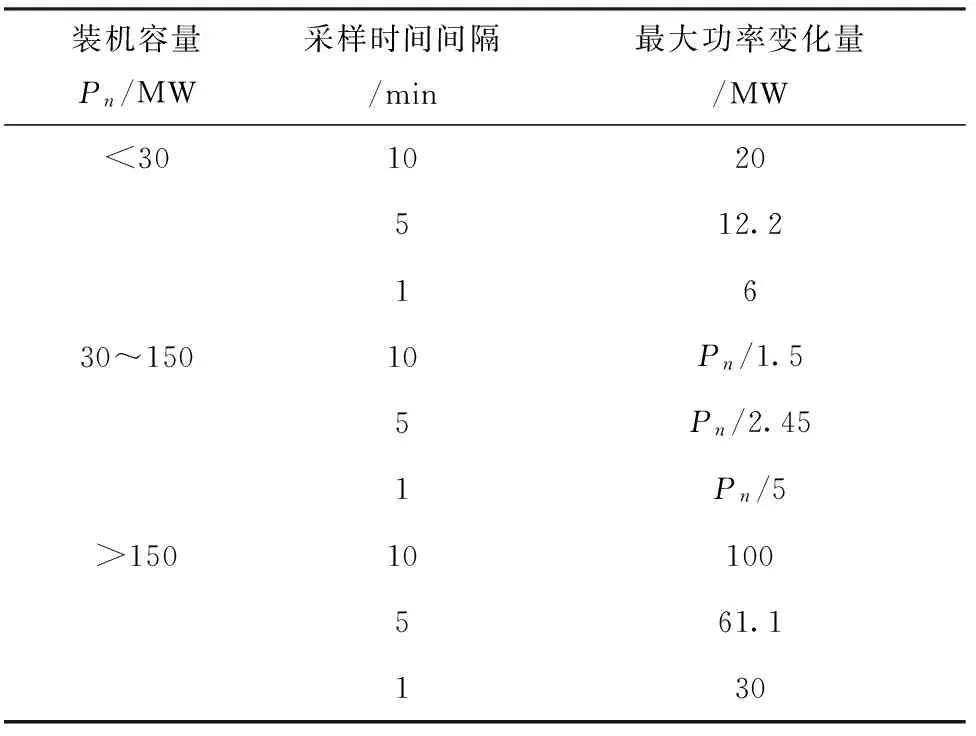
表1 不同装机容量及不同采样时间间隔下风电场最大功率变化量推荐值

在表1中,Pn为风电场额定装机容量;Pn/1.5为风电场装机容量在30～150 MW其最大功率变化量,即额定装机容量除以1.5。如装机容量为60 MW,其最大功率变化量为40 MW。

对于不合理的数据或者断档的数据,可利用插值法进行修正或者补缺。在功率汇聚后,做持续功率曲线前,应对参与汇聚的功率进行标幺化处理,基准值为所涉及风电场的装机容量之和。

2 大规模风电场群逐级汇聚过程

2.1 大规模风电场群的划分

影响风电场群划分的因素很多,即划分区域内风电场个数(密度)、风电场装机容量、划分区域覆盖地理面积、选定范围几何轮廓等。选用正圆形几何轮廓、风电场个数、装机容量、范围半径作为影响因子进行风电的逐级汇聚,得到综合影响指数为

v=an+bS+cR

(2)

式中:a、b、c为反应不同大规模风电场群特性的参数,需要根据实际数据拟合获得;n为汇聚区域内风电场个数;S为汇聚区域内风电场总装机容量,MW;R为汇聚范围半径,km。

以综合影响指数为依据进行分级汇聚时汇聚范围的选择。

2.2 持续功率曲线的物理意义

持续功率曲线是一种打乱了时序,将输出功率标幺值由大到小顺序排列的连续曲线。使用MATLAB画出的某范围风电场群功率汇聚的持续功率曲线如图2所示。持续功率曲线可以直观地描述输出功率特性:曲线头高表示最大输出功率标幺值,与横轴交点表示年利用小时数,曲线与坐标所围面积表示输出的电能。通过对比分析不同范围风电场群的持续功率曲线,可以更直观地掌握风电场群汇聚的演化规律。

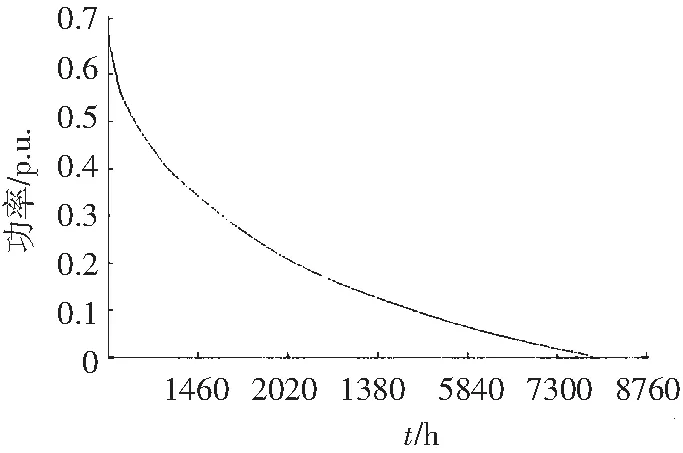
图2 持续功率曲线

2.3 逐级汇聚的过程

中国目前共有8个大规模风电场群,大规模风电场群一般由十几或几十个风电场汇集而成,装机容量能够达到GW数量级。由于不同风电场之间的风电功率相互作用,彼此加强或互补,使风电场群的总输出功率特性不同于任何单一风电场的功率特性。这需要从单一风电场的功率特性研究入手,逐级增加风电场个数,最后得到总体风电场群的功率特性。

根据地理数据作出的风电场地理分布,确定风电场分布密度最大的区域作为汇聚中心,通过式(2)划分汇聚层级,从中心风电场开始进行逐级汇聚,每级汇聚利用MATLAB作出持续功率曲线,并与大规模风电场群总汇聚的持续曲线进行拟合,分析v指数对汇聚效应的影响,最终得到汇聚的演化趋势。

3 算例分析

3.1 宁夏大规模风电场群的分级

通过式(1)计算得到各风电场与参考点的相对位置,利用定点测绘工具得到地理位置,如图3所示。

为了得到风电场逐级汇聚持续功率曲线,拟从风电场分布最密集的区域开始,选择五里坡第二风电场作为功率累加初始风电场,通过式(1)得出的相对位置关系算出各风电场距五里坡第二风电场的距离,并以距离和相对位置为衡量标准,进行风电场群的划分,如表2所示。

3.2 大规模风电场群逐级汇聚演化过程

以上一节风电场群划分区域为基础,从五里坡第二风电场开始功率的汇聚。由于五里坡第一和第二风电场在地理上紧邻,因此将五里坡第一和第二风电场输出功率按相对时间累加后做持续功率曲线,如图4、图5所示。

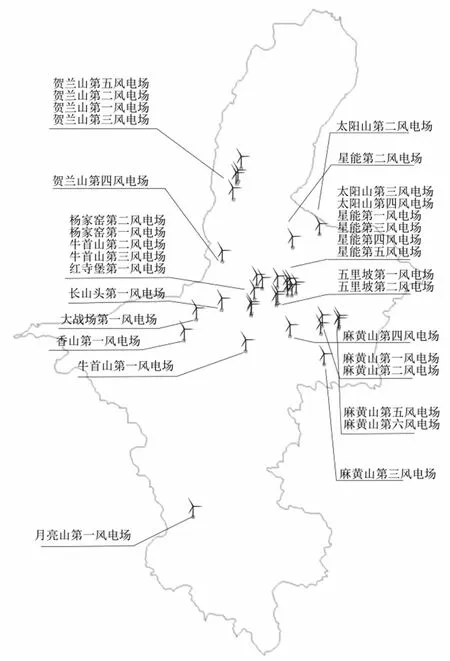
图3 二维平面的各风电场地理分布地理

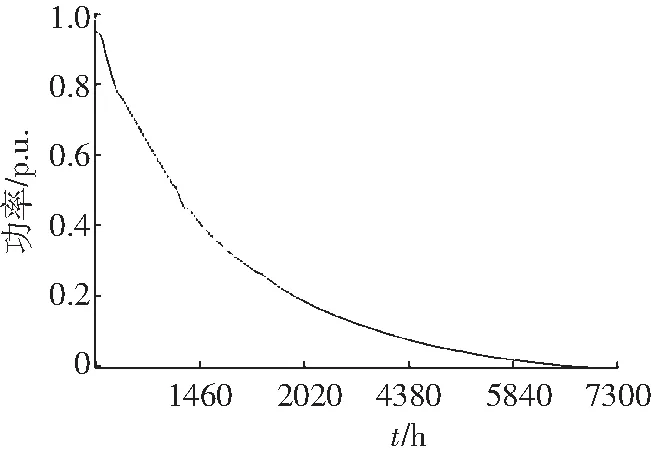
图4 五里坡第二风电场持续功率曲线

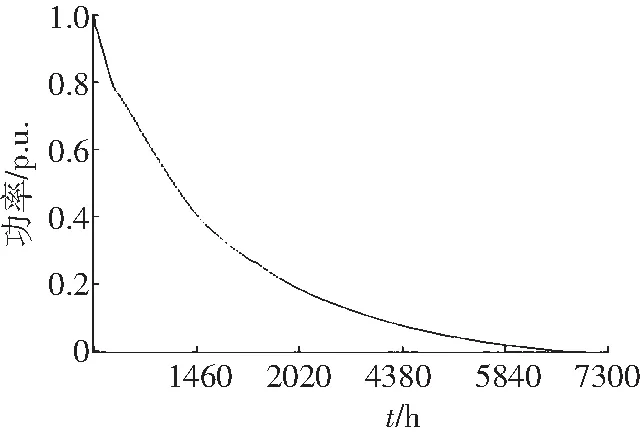
图5 五里坡风电场汇聚持续功率曲线

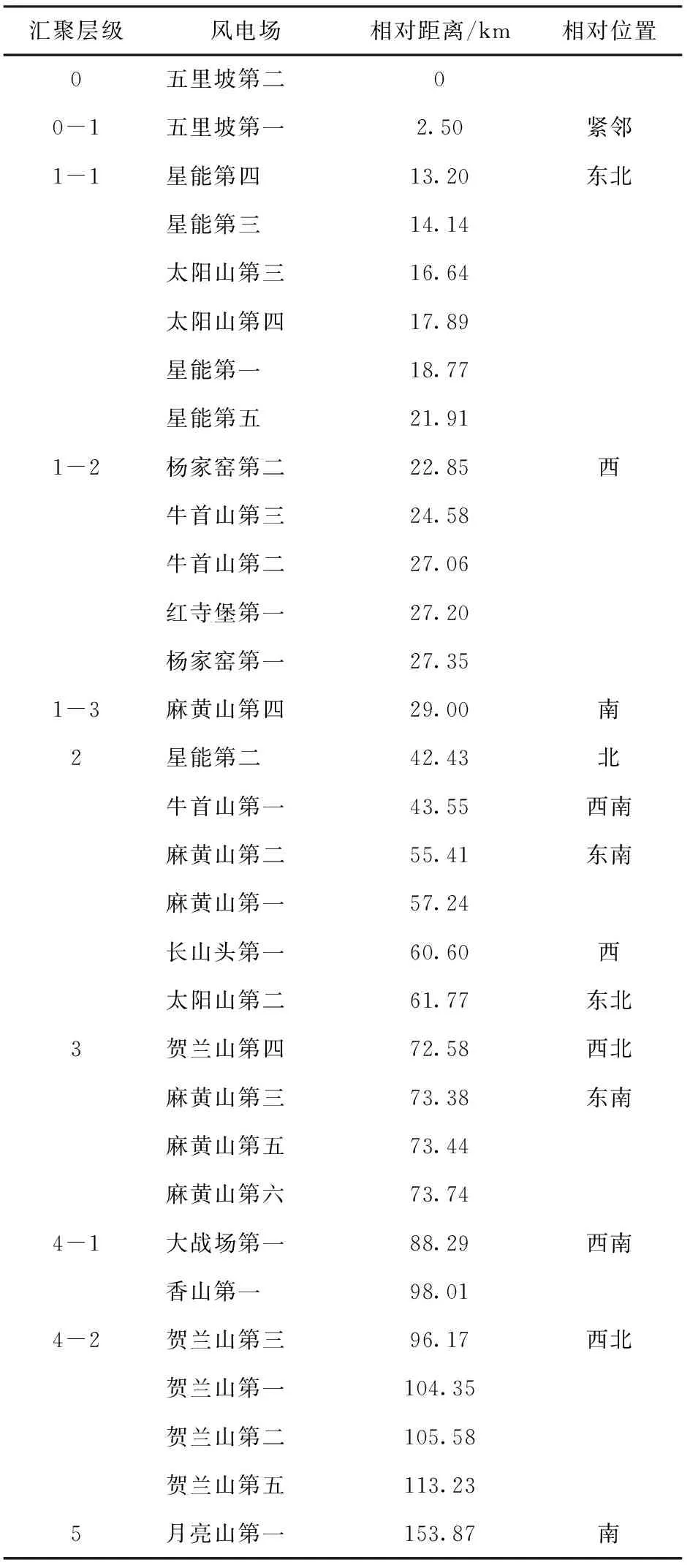
汇聚层级风电场相对距离/km相对位置0五里坡第二00-1五里坡第一2.50紧邻1-1星能第四13.20东北星能第三14.14太阳山第三16.64太阳山第四17.89星能第一18.77星能第五21.911-2杨家窑第二22.85西牛首山第三24.58牛首山第二27.06红寺堡第一27.20杨家窑第一27.351-3麻黄山第四29.00南2星能第二42.43北牛首山第一43.55西南麻黄山第二55.41东南麻黄山第一57.24长山头第一60.60西太阳山第二61.77东北3贺兰山第四72.58西北麻黄山第三73.38东南麻黄山第五73.44麻黄山第六73.744-1大战场第一88.29西南香山第一98.014-2贺兰山第三96.17西北贺兰山第一104.35贺兰山第二105.58贺兰山第五113.235月亮山第一153.87南

由图4、图5可以看出,单独风电场输出功率标幺值多数集中于0.4～0.6区域,有效利用小时数在7300 h以内,弃风严重。两紧邻的风电场持续功率曲线几乎一致,汇聚后的持续功率曲线与其差距很小,这也符合实际情形。

接着加入12个风电场参与第一级汇聚(30 km范围内),并根据其相对位置划分为三部分:东北方向、西方向、南方向。由第0级汇聚过程可知,紧邻的风电场风电特性一致性很强,分别绘出了东北方向6场汇聚持续功率曲线、西方向5场汇聚持续功率曲线,如图6、图7所示。

由图6、图7可以看出,两地区的持续功率曲线有较大差异,总体看出风电趋于弱势,即弃风严重;随着参与汇聚的风电场数目增加,曲线头高明显下降。

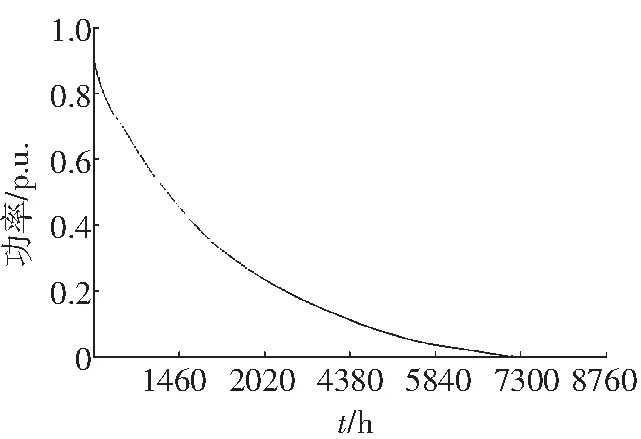
图6 东北方向6场汇聚持续功率曲线

图7 西方向5场汇聚持续功率曲线

绘出第一级汇聚的持续功率曲线,与0级汇聚相比较,如图8所示。

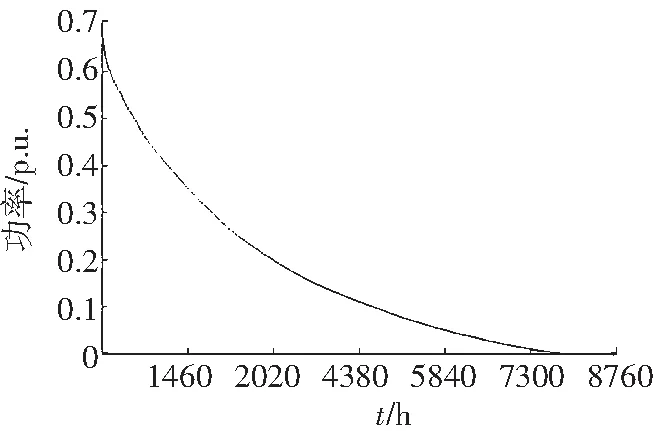
图8 第一级汇聚持续功率曲线

由图8可以看出，第一级汇聚后,弃风现象有所改善,但不明显,说明较小范围内的汇聚对功率平衡的改善不明显。

第二级汇聚(65 km范围内)加入的风电场没有明显的小区域划分,6个风电场分布较为分散。第二级汇聚持续功率曲线,如图9所示。

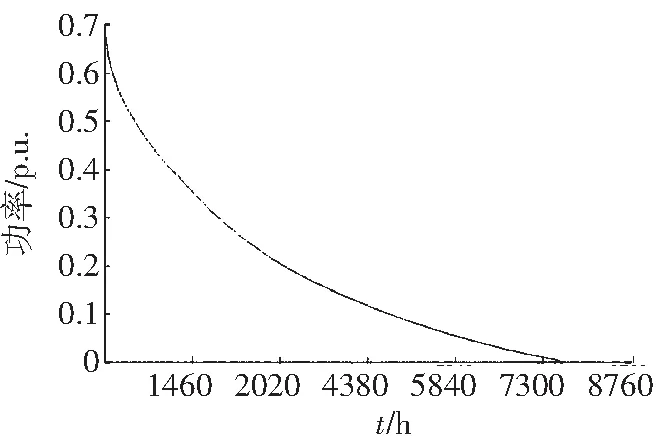
图9 第二级汇聚持续功率曲线

与第一级汇聚相比较,可以看出二级汇聚后,弃风现象进一步改善,且效果强于上级。汇聚新加入的风电场分布越分散,其抑制弃风作用越强。

第三级汇聚(80 km范围内)新加入4个风电场,只有一个装机容量为79.5 MW的风电场方位与其他3场(总装机容量269.8 MW)不同。本级汇聚与上一级汇聚范围差别较小,汇聚效果相似,可反向推知风电场群覆盖范围越广,其包含风电场分散程度越高,抑制弃风作用越强。

第四级汇聚再加入5个风电场,其中西北区域有4个风电场,与上一级东南区域3个风电场遥相呼应。汇聚后其持续功率曲线有较为明显的变化,弃风损失较上一级明显减少。由此可知风电场地理位置的平衡对风电场群中各风电场的利用程度和总输出功率的平稳起积极作用。

最后加上距离较远的月亮山第一风电场的功率数据,绘出宁夏地区大规模风电场群总持续功率曲线,如图10所示。

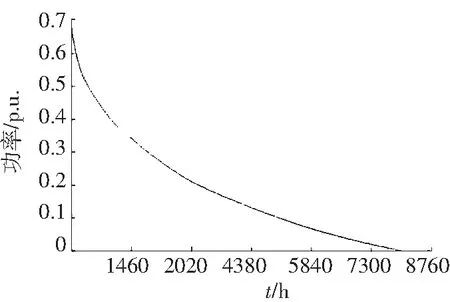
图10 宁夏地区大规模风电场群汇聚持续功率曲线

虽然月亮山第一风电场在地理位置上与其他风电场差别极大,但是一个风电场作用有限,对整体功率的分布影响不明显,总持续功率曲线与上级几乎没有差别。

4 结 论

1) 单独风电场即使处于大规模风电场群中心区域,其功率持续曲线也与总体汇聚后的持续功率曲线有较大差别。

2) 大规模风电场群功率汇聚后,最大输出功率明显下降,年利用小时数延长,即风电场规模增大,风的不确定性使各风电机组不会同时满发,其最大出力下降;各风电机组同时停运的概率下降,总发电时长增加。

3) 在第三级汇聚后(即20个风电场功率汇聚后),持续功率曲线基本定型,差别不大,说明地理位置联系紧密且在数量上占优势的风电场群可以决定大规模风电场群功率汇聚的趋势。

[1] 张卫红,于吉庆,王坤.新能源发电并网标准比较[J].黑龙江电力,2011,33(6):403-408.ZHANG Weihong,YU Jiqing,WANG Kun.Comparision of standards for grid connected system of new energy generation[J].Heilongjiang Electric Power,2011,33(6):403-408.

[2] 杨茂,贾云彭,钱为,等.基于动态权重的风电功率组合预测方法研究[J].东北电力大学学报,2013,33(1):131-136.YANG Mao,JIA Yunpeng,QIAN Wei,et al.A combination method research for wind power predication based on dynamic weight[J].Journal of Northeast Dianli University,2013,33(1):131-136.

[3] 侯佑华,房大中,齐军,等.大规模风电入网的有功功率波动特性分析及发电计划仿真[J].电网技术,2010,34(5):60-66.HOU Youhua,FANG Dazhong,QI Jun,et al.Analysis on active power fluctuation characteristics of large-scale grid-connected wind farm and generation scheduling simulation under different capacity power injected from wind farms into power grid,2010,34(5):60-66.

[4] 林今,孙元章.基于频域的风电场功率波动仿真(一)模型及分析技术[J].电力系统自动化,2011,35(4):65-69.LIN Jin,SUN Yuanzhang.Simulation of power fluctuation of wind farms based on frequency domain Part One Model Analysis Technique[J].Automation of Electric Power SYSTEMS,2011,35(4):65-69.

[5] 潘迪夫,刘辉,李燕飞.风电场风速短期多步预测改进算法[J].中国电机工程学报,2008,28(26):87-91.PAN Difu,LIU Hui,LI Yanfei.Optimization algorithm of short-term multi-step wind speed forecast,2008,28(26):87-91.

[6] 南晓强,李群湛,邱大强.基于符号时间序列法的风电波动分析与预测[J].中国电力,2013,46(4):75-79.NAN Xiaoqiang,LI Qunzhan,QIU Daqiang.Analysis and forecast of wind power fluctuation based on symbolized time series theory[J].Electric Power,2013,46(4):75-79.

[7] 刘玉.基于实测数据分析的大型风电场风电功率预测研究[J].黑龙江电力,2011,33(1):11-15.

LIU Yu.Study on wind power prediction of large-scale wind farm based on real data analysis[J].Heilongjiang Electric Power,2011,33(1):11-15.

[8] 崔杨,穆钢,刘玉,等.风电功率波动的时空分布特性[J].电网技术,2011,35(2):110-114.CUI Yang,MU Gang,LIU Yu,et al.Spatiotemporal distribution characteristics of wind power fluctuation[J].Power System Technology,2011,35(2):110-114.

[9] Bernhard Hasche.General statistics of geographically dispersed wind power[J].Wind Energy,2010,13(1):773-784.

[10] Hannele Holttinen.Hourly wind power variations in the Nordic countries[J].Wind Energy,2005,8(5):173-195.

[11] 黄裕春,杨甲甲,文福拴.计及接纳间歇性电源能力的输电系统规划方法[J].电力系统自动化,2013,37(4):28-33.HUANG Yuchun,YANG Jiajia,WEN Fushuan.Transmission system planning considering the capability of accommodating intermittent generation sources[J].Automation of Electric Power Systems,2013,37(4):28-33.

(责任编辑 侯世春)

Analysis of the gradual convergence evolution of large scale wind farms

ZHAO Shu1,CUI Tianli2

(1.School of Electrical Engineering,Northeast Dianli University,Jilin 132012,China; 2.Power Supply Company in Fushan District of Yantai City,State Grid Shandong Electric Power Company,Yantai 264000,China)

Aiming at the affect of data loss to the entire output power of large-scale wind farms,the author expounded the wind power characteristics of continuous power curve description and researched the impact of geographical distribution on convergence effect of large scale wind farms,according to geographic and power data of large-scale wind power in Ningxia area.Also,the evolution law of continuous power curve was analyzed under the influence of wind power farm distribution and the method to study large scale wind farms was put forward according to the geographical correlation hierarchical convergence.Practice has proved that the way to analyze the gradual convergence evolution of large scale wind farms can solve the data loss problems of large scale wind power planning,power prediction and other practical projects.

large scale wind farms; convergence effect; continuous power curve; geographical distribution of wind power farms

2016-06-24;

:2016-07-24。

赵 姝(1990—),女,硕士,研究方向为大规模风电场群场景的电力系统规划。

TM614

A

2095-6843(2016)06-0487-05