自适应多小波混合构造方法及在故障诊断中应用

袁 静 ， 魏 颖， 訾艳阳， 王志诚， 倪修华

(1. 上海无线电设备研究所，上海 200090； 2. 西安交通大学 机械制造系统工程国家重点实验室，西安 710049)

自适应多小波混合构造方法及在故障诊断中应用

袁 静1， 魏 颖1， 訾艳阳2， 王志诚1， 倪修华1

(1. 上海无线电设备研究所，上海 200090； 2. 西安交通大学 机械制造系统工程国家重点实验室，西安 710049)

小波理论中基函数的逼近阶和消失矩特性都是信号处理中非常重要的性质。传统自适应多小波构造方法仅能对逼近阶或消失矩单一特性进行改造，并且所生成的多个基函数时频特征和波形差异较小，难以有效实现复杂动态故障的自适应提取与识别。为此，提出基于两尺度相似变换和提升方法相结合的自适应多小波混合构造框架，对原有多尺度函数和多小波函数进行线性与非线性组合，扩大多小波改造空间，获得具有高阶逼近阶的多尺度函数和消失矩涵盖多阶次的多小波函数，增强多小波正则性、光滑性、信号逼近能力和局部定位能力，并提高信号分析精度，为复杂动态信号中微弱和复合故障特征提取与识别提供优良性质的自适应基函数及诊断方法;为按需优选自适应基函数，提出改进局部故障域谱熵最小化原则的自适应基函数优选方法，实现轴系、齿轮和轴承故障的分门别类优选，简化故障分类模式。工程实例表明该方法可以有效识别复杂背景噪声干扰下的轴承内圈微弱损伤，并成功诊断出空气分离压缩机组齿轮箱止推夹板碰撞与摩擦的多特征复合故障。

多小波；两尺度相似变换；提升变换；特征提取；故障诊断

准确及时识别运行中萌生和演变的损伤故障，对于保障国民经济行业中的关键设备安全可靠运行，避免经济损伤和人员伤亡意义重大。然而工程实际中的关键设备结构复杂，部件众多，采集到的故障动态信号是各部件响应的综合反映，且复杂多变的传递途径、恶劣工况下强背景噪声干扰、多激励源相互耦合等因素影响增加了动态信号的复杂程度。近年来，机械故障诊断内积变换方法为复杂动态信号中的故障特征提取与识别提供灵活有效方法。它运用与故障特征相似或相关的基函数匹配信号中的故障特征，获得不同物理意义并符合工程实际的故障征兆，从而实现科学、正确的状态监测与故障诊断[1]。

在内积变换原理的信号处理方法中，近年来兴起的多小波变换是小波理论的新发展，其多分辨分析是由多尺度函数生成，通过多小波函数的伸缩和平移构成空间RIESZ基[2]。由于它兼备单小波所不能同时具备的多种优良性质[3]以及多个时频特征有所差异的基函数，这使得多小波变换在早期和微弱故障特征提取、复合故障特征识别等方面展现显著优势[4-6]。基于机械故障诊断内积变换原理，构造和选择合适的多小波基函数是实现有效特征提取与合理故障诊断的关键。为此，国内外学者开展基于两尺度相似变换[7-8]、对称提升变换[9-10]、非对称提升变换[11-12]和重数延长理论[13]的自适应多小波基函数构造方法研究，以获得与故障特征波形相匹配的自适应基函数，并成功应用于齿轮轴承试验台、电力机车、连铸连轧机组、烟气轮机等关键设备故障诊断。

多尺度函数的逼近阶和多小波函数的消失矩都是小波理论中重要特性，对故障特征准确提取与识别具有重要意义。以上这些构造方法中，两尺度相似变换可构造出一对新的对称双正交多小波，但它在增强多尺度函数的逼近阶同时，却以削弱多小波函数的消失矩为代价。虽然提升方法可以改变多小波函数的消失矩，但多尺度函数本身及其逼近阶却保持不变，这使得多尺度函数性质不理想并且导致对蕴含故障征兆丰富的最低频信号无法实施自适应故障提取。因此，难以通过单一多小波构造方法同时获得兼备优良逼近阶和消失矩特性的多小波。同时，现有多小波构造方法所生成的多个基函数时频特征和波形差异并不大，难以有效匹配特征各异的复合故障。

因此，本文提出基于两尺度相似变换和提升方法相结合的自适应多小波混合构造框架，对原有多尺度函数和多小波函数进行线性与非线性组合，扩大多小波改造空间，提高信号分解和重构精度，构造兼具优越逼近阶和多阶消失矩特性的自适应多尺度函数和多小波函数，为复杂动态信号中微弱和复合故障特征最佳匹配提供优良性质自适应基函数。为按需优选自适应基函数，提出改进局部故障域谱熵最小化原则的自适应基函数优选方法，实现轴系、齿轮和轴承故障的分门别类优选，并通过多层次精细化的多小波包变换实现故障特征的有效提取与故障识别。最后，将该方法应用于电力机车轴承内圈微弱损伤识别和空气分离压缩机组复合故障诊断以验证有效性与实用性。

1 多小波基础理论

设Φ(t)=[φ1(t),φ2(t),…,φr(t)]和Ψ(t)=[ψ1(t),ψ2(t),…,ψr(t)]分别为r重多尺度函数和多小波函数，根据两尺度矩阵方程，多小波包分解可表示为

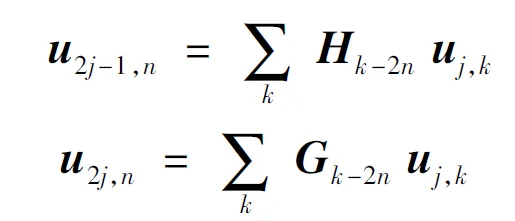
式中:u2j-1,n和u2j,n分别为第2j-1频带和第2j频带的第n个分解样本点，{Hk}和{Gk}分别为多小波低通和高通滤波器组。同样，多小波包重构公式为

式中:符号*表示共轭转置。相对于多小波变换，多小波包分析能对信号进行全频带多层次划分，为信号提供一种频带更加精细的分析方法。

由于多小波包的分解和重构是一个多输入多输出系统，对实际采样的一维输入信号必须进行矢量化前处理以产生多输入信号，其中重复采样的前处理方法对信号降噪效果较好，故在本文中采用。为获得故障特征信息的多维度丰富表征，本文采用改进的多小波后处理方法[14]，直接输出多维矢量信号。

2 多小波混合构造方法

逼近阶是刻画多尺度函数最重要的性质之一，对于信号分解和重构具有重要价值。对应于逼近阶，消失矩是多小波函数的重要性质之一，用于描述基函数光滑性与局部化能力。特别地，对于双正交多小波而言，若多尺度函数具有n阶逼近阶，多小波函数具有p阶消失矩，则其对偶多尺度函数具有p阶逼近阶，对偶多小波函数具有n阶消失矩。下面将利用多小波混合构造框架同时改造多小波的逼近阶和消失矩，为复杂动态信号中微弱和复合故障特征准确提取提供具有优良特性的自适应多小波。

2.1 两尺度相似变换

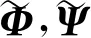
(3)

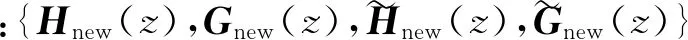
2.2 提升变换

(4)

2.3 基于两尺度相似变换和提升方法相结合的多小波混合构造框架

针对以上构造理论的不足，本文提出基于两尺度相似变换和提升方法相结合的多小波混合构造框架，采用两尺度相似变换对现有多小波系统进行多次改造，获得性能优越多尺度函数，然后采用提升变换对改造后性能欠佳的多小波函数进行改善，最终获得兼具优良逼近阶和消失矩特性的多小波，有效提高复杂动态信号中自适应故障特征匹配准确性与有效性。

在众多多小波中，GHM多小波是最常用的二重多小波，具有紧支性、对称性、正交性及2阶逼近阶和2阶消失矩[15]。下面将以GHM多小波为研究对象，构建多小波混合构造框架。

根据两尺度相似变换矩阵求解算法，对GHM多小波设计转换矩阵M1(z)

(5)

式中:自由参数a和b为非零常数。

(6)

式中:参数c,d和e依旧为非零常数。

以两次两尺度相似变换中a=1，b=-0.8，c=1，d=2，e=1.5为例，计算得到7阶消失矩的提升矩阵为

式中:x和y分别为提升自由参数。可见，混合构造方法生成的多小波受到自由参数a,b,c,d,e,x和y的共同作用。图 1为a=1，b=-0.8，c=1，d=2，e=1.5，x=2和y=1的多小波算例。从图 1可以看到，该基函数呈现出明显的振荡衰减形状，非常类似于由局部故障所引起的冲击响应波形。与初始GHM多小波相比，经混合构造后的新多小波各基函数差异性扩大，同时逼近阶和消失矩都得到改善，其正则性、光滑性和局部定位能力得到极大的增强，使得其综合特性得到提升，有利于它们在信号特征提取中的应用。

(a) 多尺度函数φ1(b) 多尺度函数φ2

(c) 多小波函数ψ1(d) 多小波函数ψ2图1 混合构造多小波算例

Fig.1 Multiwavelets example by the hybrid construction method

3 改进局部故障域谱熵最小化原则的自适应基函数优选方法

谱熵顾名思义即是谱的熵。对于信号包络谱F={f(k)}，其包络谱熵Sh(F)可计算为

(8)

局部性故障发生时，其时域波形常表现为周期性冲击的调制信号，通过包络谱可以有效检测出冲击的周期性。因此，为获取与故障特征相关的基函数，可根据包络谱熵来判定基函数匹配性能的好坏。由于不同类机械故障，其包络谱将表现出不同的故障特征。针对常见的轴系、齿轮和轴承故障特征进行分类，研究局部故障域谱熵最小化原则并在自适应基函数优选及故障征兆识别中展现出优势。工程实际中，轴系和齿轮故障均表现为与转频相关的特征，为此本文将局部故障域谱熵最小化原则中的轴系故障和齿轮故障进行合并，提出改进局部故障域谱熵最小化原则，简化故障分类模式并减少基函数优选时间，从而最佳匹配出待测信号中的动态故障特征。

(1)轴系和齿轮故障的局部故障域谱熵最小化原则

轴系故障的包络谱主要表征为转频及其次倍频。齿轮故障的包络谱主要表现为齿轮转频(即旋转轴转频)和啮合频率及其倍频。为获得有利于故障诊断的转频及其次倍频信息，将轴系和齿轮故障的局部故障域定义为包含转频次频到倍频范围，避开齿轮信号中较为明显的啮合频率的影响。假设轴和齿轮的转频为f，齿轮啮合频率为fm，则该局部故障域ff定义为

ff=[fmin,fmax]

(9)

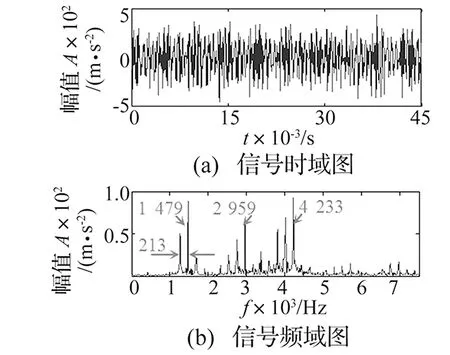
式中:fmin≤f/3且2f≤fmax

(2)轴承故障的局部故障域谱熵最小化原则

轴承故障的包络谱主要谱线分别为明显的工频、轴承故障特征频率及其倍频。为有效提取出隐藏在背景噪声中的轴承故障特征频率，将滚动轴承故障特征频率涵盖的频域定义为轴承局部故障域，避免工频对于轴承故障诊断的影响。假设滚动轴承保持架、外圈、内圈和滚动体故障特征频率分别为fc、fo、fi和fel，轴承局部故障域定义为

ff=[fc-Δ,fc+Δ]∪[fmin-Δ,fmax+Δ]

(10)

式中:fmin=min(fo,fi,fel)且fmax=max(fo,fi,fel);Δ为一个小的邻域。

因此，针对不同的研究对象，可根据式(9)和式(10)计算局部故障域ff，利用式(8)的谱熵计算公式获得局部故障域的平方包络谱熵值，以改进局部故障域谱熵值最小化原则优选内积匹配过程中的自适应基函数。

综上所述，为有效识别机械故障特征，基于多小波混合构造框架的自适应基函数构造和改进局部故障域谱熵最小化原则的自适应基函数选择过程见图2。其中，选择经典遗传算法为优化工具，a，b，c，d，e范围均为[10,0)∪(0,10]，x、y范围设定为[-50,50]，选用算术交叉算子和非均匀变异算子，种群规模和初始种群个数分别设置为30，交叉概率设定为0.6，变异概率设定为0.05。可见，通过自适应基函数构造和选择流程，可获得性能优越且与信号自适应的基函数及其合适的消失矩，同时可选定适宜的多小波包分析频带。

4 试验信号分析

大型复杂动力装备的滚动轴承运行在高速、重载和强冲击等恶劣环境下，极易发生擦伤、点蚀、剥落和磨损等损伤类故障。滚动轴承故障诊断是典型的非平稳信号处理与微弱信号特征识别问题。特别是轴承内圈故障，由于传递途径远、特征强弱变化不均以及强背景噪声干扰等因素，使得它成为滚动轴承故障识别难点之一。为保障装备安全运行，预防重大事故发生，将自适应多小波混合构造方法应用于大型复杂动力装备轴承监测诊断。

图3 电力机车轴承内圈轻微擦伤故障

某电力机车轴承552732QT存在内圈轻微擦伤故障，如图 3所示。将该轴承在机车滚动轴承试验台上进行测试。为尽可能模拟实际工况，采用液压系统来驱动和加载，振动加速度传感器安装于轴承外圈垂直方向的加载模块上，通过加载模块对故障响应信号实现传递和削弱。测试时，转轴的转速为602 r/min，采样频率为12.8 kHz。根据转速和轴承几何参数，计算得到轴承保持架、外圈、内圈和滚动体故障特征频率分别为4.25 Hz、72.39 Hz、98.17 Hz和64.88 Hz。

采集测试轴承运行的振动信号如图 4所示。其时域和频域信号成分丰富，难以识别出与轴承内圈损伤相关的故障特征。对该信号采用图 2的基于混合构造框架的自适应多小波方法进行分析，采用多小波包2层分解，根据式(10)计算得到轴承局部故障域ff=[3,5]∪[60,102]。由此构造和优选的多小波具有4阶逼近阶和3阶消失矩，参数a=-7.46，b=-0.87，c=-5.06，d=-0.83，e=4.97，x=30.42和y=-15.65，且最优的分析信号为多小波包分解后的第1频带第2分支信号，其分解信号及平方包络谱如图5所示。可以清晰看到，图 5(a)的时域分析结果出现较为明显的转频为间隔的周期性冲击(黑色三角形示意)，且各冲击附近出现若干间隔约为Ti=0.01 s的内圈故障冲击特征。同时，图 5(b)的包络谱分析结果中出现突出的内圈故障特征频率98.44 Hz及其二倍频197.7 Hz。除此之外，轴承的转频10.13 Hz及其倍频也相当明显。

采用非自适应GHM多小波、与自适应多小波消失矩相同的db3单小波对测试信号进行对比分析。为统一比较，对比基函数的分解输出频带均与自适应多小波相同。由于包络谱分析更利于轴承故障识别，为此将各对比方法的平方包络谱显示如图 6所示。图中除了明显的轴承转频及其谐波分量外，没有突出的轴承内圈故障特征频率，无法为轴承故障的合理诊断提供有力依据。可见，本文所提出的自适应多小波混合构造方法可以有效地提取与识别复杂背景干扰下的轴承内圈微弱损伤特征，同时轴承故障的局部故障域谱熵最小原则可以很好地避免工频成分的干扰，有利于故障特征清晰提取与故障准确诊断。

图4 测试轴承振动信号

图5 测试轴承振动信号的自适应多小波分析结果

图6 测试轴承振动信号的对比分析结果

5 工程实例

某炼油厂空气分离压缩机组由电机、齿轮箱、压缩机等组成，并设计止推夹板用于斜齿轮啮合传动时轴向力传递，其结构简图如图 7所示。机组在某次大修后开机发现齿轮箱振动剧烈，并伴随尖叫声，但机组整体轴向振动不大，并且轴瓦温度正常。为此，采用加速度传感器对机组进行监测诊断，采样频率设置为15 000 Hz，齿轮箱低速轴和高速轴转频分别为49.75 Hz和212.99 Hz，齿轮啮合频率为6 815.75 Hz。图 8为采集的齿轮箱5#测点的振动信号及其频谱，其时域信号呈现强烈振荡特性，频谱中存在三个主频率，并伴随高速轴转频213 Hz的边频带。据此只能推测该机组故障与齿轮箱高速轴或其小齿轮相关，无法获得更为准确的故障信息。

图7 空气分离压缩机结构图

图8 空气分离压缩机组振动信号

为更好地提取机组故障特征为故障确诊提供依据，采用自适应多小波混合构造方法按照图 2的分析流程对该机组振动信号进行分析，其中实施1层多小波包分解，根据式(9)设计轴系和齿轮故障的局部故障域ff=[60,500]。由此构造和选择的多小波具有4阶逼近阶和7阶消失矩，参数a=6.29，b=4.12，c=5.02，d=-8.21，e=-7.87，x=-8.26和y=4.54，且最优分析结果为多小波分解后的第2频带第1分支信号，如图 9 (a)所示。为利于故障特征的多维度表征，输出同频带第2分支信号，如图 9(b)所示。从图 9 可以看到，最优的第1分支结果中出现了一系列在间隔周期上具有规律性的冲击特征I1和I2，其时间间隔以T1=4 ms和T2=5.4 ms交替出现。并且，T1和T2的平均周期为4.7 ms，对应于高速轴旋转周期。更加重要的是，每组I1或I2之间的时间间隔T1+T2=9.4 ms恰好为高速轴旋转周期的2倍，即对应于高速轴转频的1/2。同时，第2分支结果表现为明显的幅值调制特征，其调制周期T3同为4.7 ms，而载波周期T4约为0.675 ms，即约为1 481.5 Hz，对应于图 8(b)的三个主频率之一。同样，采用GHM多小波和db7单小波进行对比分析，两者输出频带均与自适应多小波相同，如图10(a)和图10(b)所示。对比分析结果较为杂乱，仅存在几处不够清晰的冲击特征。同时，输出对比结果的包络谱如图11(a)和图11(b)所示。两种包络谱中转频及二倍频均较为突出，虽然存在转频的1/2次谐波分量，但其在包络谱中不是十分明显。

图9 空气分离压缩机组振动信号的自适应多小波分析结果

图10 空气分离压缩机组振动信号的对比分析结果

图11 空气分离压缩机组振动信号的对比分析结果包络谱

由于频谱中与齿轮局部故障相关的齿轮啮合频率并不明显，且调制分析结果中调制频率也并非齿轮啮合频率，因此可以推断齿轮本身并没有局部损伤，而是与其转频相关的故障。研究表面，旋转机械的碰摩故障往往表征为1/2倍工频的次谐波频率特征[17]。结合现场齿轮箱剧烈振动、刺耳尖叫声以及所提取的故障征兆，可以判断该机组齿轮箱高速轴小齿轮附近存在碰摩故障，同时存在外力碰撞使得每旋转一周出现一次冲击特征，并激发幅值调制现象。

通过对图7的机组结构仔细分析发现，止推夹板设计存在缺陷。由于加工和安装误差，小齿轮两侧的止推夹板与大齿轮端面不是严格平行，致使机组运行中大齿轮与止推夹板之间产生碰撞与摩擦，其中碰撞导致小齿轮每旋转一周内出现一次冲击，进而诱发信号中的幅值调制现象，而摩擦所衍生的非线性因素造成冲击间隔的规律性变化以及1/2次谐波频率的碰摩征兆。故障确诊后，重新装配齿轮箱并打磨止推夹板与大齿轮接触面，开机后振动明显降低，尖叫声消失。以上机组故障现象与诊断分析结果一致，工程实例显示基于自适应多小波混合构造方法可以有效提取冲击和碰摩故障特征以及幅值调制的复合故障多重特征，而对比方法难以实现故障征兆的有效提取以及正确故障诊断。

6 结 论

(1)为实现优良性质基函数的构造，本文提出基于两尺度相似变换和提升方法相结合的自适应多小波混合构造框架。首先采用两尺度相似变换对原始多小波进行多次改造，获得具有高阶逼近阶的多尺度函数，提高多尺度函数逼近性能和分析精度。然后采用提升变换对改造后性能欠佳的多小波函数进行改善，获得消失矩涵盖多阶次的多小波函数，增强多小波正则性、光滑性和局部定位能力。由此构造出兼具优越逼近阶和多阶消失矩特性的自适应多尺度函数和多小波函数，为复杂动态信号中微弱和复合故障特征提取与识别提供优良性质自适应基函数及诊断手段。

(2)鉴于轴系和齿轮的故障特征相似性，提出改进局部故障域谱熵最小化原则，实现轴系、齿轮和轴承故障的分门别类优选，简化故障分类模式并减少基函数优选时间，从而优选出与待测动态信号故障特征相匹配的最优基函数，实现基于内积变换原理的故障特征准确提取与合理诊断。

(3)将本文方法应用于电力机车轴承故障识别，有效地提取与识别复杂背景噪声干扰下的轴承内圈微弱损伤特征，同时轴承故障的局部故障域谱熵最小化原则可以很好地避免工频成分的干扰，有利于故障特征清晰提取与准确诊断。同时将该方法应用于空气分离压缩机组故障诊断，有效提取出1/2次谐波的规律性冲击序列特征以及幅值调制特征，成功诊断出齿轮箱止推夹板碰撞与摩擦的多特征复合故障。

(4) 特别需要指出的是，优化时间较长是自适应多小波构造中最大缺点。因此本方法更加适合离线精密故障诊断，在工程实践中可通过选用更快捷的优化算法来提升运算速度。同时，当诊断分析精度要求不高时，建议将提升变换中消失矩优选范围缩小为5～7阶。

[ 1 ] 何正嘉，袁静，訾艳阳. 机械故障诊断的内积变换原理与应用[M]. 北京：科学出版社，2012.

[ 2 ] 程正兴，张玲玲. 多小波分析与应用[J]. 工程数学学报，2011，18(1)：99-107. CHENG Zhengxing, ZHANG Lingling. Analysis of multiwavelet and application[J]. Chinese Journal of Engineering Mathematics, 2011，18(1)：99-107.

[ 3 ] Daubechies I. Ten lectures of wavelets[C]//CBMS-NSF Regional Conference Series in Applied Mathematics. Society for Industrial and Applied Mathematics: Philadelphia, 1992.

[ 4 ] 吴宏钢，秦毅，秦树人.基于重分配配算法和奇异值分解的多小波脊线提取[J].振动与冲击, 2009, 28(12): 9-11. WU Honggang, QIN Yi, QIN Shuren. Multiwavelet ridge extraction based on reassigning algorithm and singular value decomposition[J]. Journal of Vibration and Shock, 2009, 28(12): 9-11.

[ 5 ] 张建宇，李文斌，张随征，等. 多小波自适应阈值降噪在故障诊断中的应用[J]. 北京工业大学学报，2013，39(2)：166-173. ZHANG Jianyu, LI Wenbin, ZHANG Suizheng, et al. Application of multiwavelet adaptive threshold denoising in fault diagnosis[J]. Journal of Beijing University of Technology, 2013，39(2)：166-173.

[ 6 ] JIANG H H, Li C, L H. An improved EEMD with multiwavelet packet for rotating machinery multi-fault diagnosis[J]. Mechanical Systems and Signal Processing, 2013, 36: 225-239.

[ 7 ] STRELA V. Multiwavelets: theory and application[D]. Cambridge: Massachusetts Institute of Technology, 1996.

[ 8 ] YUAN J, HE Z J, ZI Y Y, et al. Adaptive multiwavelets via two-scale similarity transforms for rotating machinery fault diagnosis[J]. Mechanical Systems and Signal Processing, 2009, 23 (5): 1490-1508.

[ 9 ] DAVIS G, STRELA V, TURCAJOVA R. Multiwavelet construction via the lifting scheme[C]// Wavelet Analysis and Multiresolution Methods, T-X He, Ed New York: Marcel Dekker,1999, Lecture Notes in Pure and Applied Mathematics, 1999.

[10] WANG X D, ZI Y Y, HE Z J. Multiwavelet construction via an adaptive symmetric lifting scheme and its applications for rotating machinery fault diagnosis[J]. Measurement Science and Technology, 2009, 20, 045103.

[11] KEINERT F. Raising multiwavelet approximation order through lifting[J]. SIAM. J. MATH. ANAL, 2001, 32: 1032-1049.

[12] YUAN J, HE ZJ, ZI YY, et al. Construction and selection of lifting-based multiwavelets for mechanical fault detection[J]. Mechanical Systems and Signal Processing, 2013, 40: 571-588.

[13] CHEN J L, ZUO M J, ZI Y Y, et al. Construction of customized redundant multiwavelet via increasing multiplicity of fault detection of rotating machinery[J]. Mechanical Systems and Signal Processing, 2014, 42: 206-224.

[14] 袁静，何正嘉，訾艳阳. 基于提升多小波的机电设备复合故障分离和提取[J]. 机械工程学报，2010, 46 (1): 79-85. YUAN Jing, HE Zhengjia, ZI Yanyang. Separation and extraction of electromechanical equipment compound faults using lifting multiwavelets[J]. Journal of Mechanical Engineering, 2010, 46 (1): 79-85.

[15] GERONIMO J S, HARDIN D P, MASSOPUST P R. Fractal functions and wavelet expansions based on several scaling functions[J]. Journal of Approximation Theory, 1994, 78:373-401.

[16] 屈梁生. 机械故障的全息诊断原理[M]. 北京：科学出版社，2007.

[17] CHU F L, LU W X. Experimental observation of nonlinear vibrations in a rub-impact rotor system[J]. Journal of Sound and Vibration, 2005, 283(3/4/5)：621-643.

Adaptive multiwavelet hybrid construction method and applications in fault diagnosis

YUAN Jing1, WEI Ying1, ZI Yanyang2, WANG Zhicheng1, NI Xiuhua1

(1. Shanghai Radio Equipment Research Institute，Shanghai 200090, China；2. State Key Laboratory for Manufacturing Systems Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

Vanishing moments and approximation orders of basis functions are both the important properties in the wavelet theory. The traditional adaptive multiwavelet construction methods can only reform either vanishing moments or approaching orders. Meanwhile, their time-frequency characteristics and waveform differences among the new multiple basis functions are quite small to lead to difficulties of efficiently adaptive extraction and identification of complex dynamic faults. Thus, the adaptive multiwavelet hybrid construction method combined with the two-scale similarity transformation and the lifting transformation was proposed. Using linear and nonlinear combinations of multi-scaling wavelet functions to extend the construction space, the multi-scaling functions with higher approximation orders and the multi-wavelet functions covered with multiple vanishing moments were obtained to enhance the regularity, smoothness, capability of signal approaching and local positioning, and to improve the signal analysis accuracy. It provided adaptive basis functions with super properties and a diagnosis method for weak and compound fault features extraction and identification. For the optimal selection of adaptive basis functions, the improved local fault field spectral entropy minimization rules were proposed to classify typical shaft systems, gear and rolling bearing faults and to simplify fault-classifying modes. The engineering applications showed that the method can effectively identify bearing weak inner-race damages under complex background noise, and successfully diagnose impact and rubbing compound faults with multiple features from thrust splints of gearbox in air-compressors.

multiwavelet; two-scale similarity transformation; lifting transformation; feature extraction; fault diagnosis

国家自然科学基金(51405301);上海市青年科技启明星计划(16QB1403700)

2015-09-14 修改稿收到日期：2015-11-10

袁静 女，博士，高级工程师，1983年生

TH17