KCS标称伴流场的尺度效应数值分析

张海鹏，张东汗，郭春雨，王恋舟，刘恬

哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001

KCS标称伴流场的尺度效应数值分析

张海鹏，张东汗，郭春雨，王恋舟，刘恬

哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001

为了研究标称伴流场的尺度效应，对不考虑自由液面效应的KCS船的粘性绕流场进行研究，并基于RANS方法和SSTk-ω模型对包含实尺度的7种不同尺度下的标称伴流场进行数值计算。然后，将模拟结果与试验数据进行对比，进一步分析标称伴流场的尺度效应。结果显示：各半径处平均轴向伴流分数的倒数与雷诺数的对数呈正相关；KCS裸船体桨盘面处的标称伴流场存在2个伴流峰，且伴流峰值会随雷诺数的增加而减小，有利于减小螺旋桨的空泡和激振力；小尺度模型的尺度效应更为明显，且内半径处的平均轴向伴流分数尺度效应问题比外半径处的更为严重。

标称伴流场；尺度效应；KCS；数值计算

0 引 言

船舶在水中航行时会产生伴流，船舶伴流场是个十分复杂的三维速度场。螺旋桨在不均匀伴流场中工作，船、桨之间存在着相互作用，会形成空泡并会产生强烈的脉动激振力［1］。为了改善船舶航行性能，提高螺旋桨推进效率，并最终实现减振降噪的目的，需要准确预报和分析船舶伴流场。

拖曳水池中的模型试验是在傅汝德数相同，而雷诺数不一致的条件下进行的，可以认为模型的伴流分数与实船相等。在拖曳水池中，船模试验的雷诺数范围仅为106～107，但实尺度船舶在海面航行时，其雷诺数一般能达到109。雷诺数的增加会削减速度边界层的厚度，从而改变近壁区速度边界层的分布，这种因为雷诺数不同而导致实尺度与模型尺度之间伴流场差异的现象，被称之为“伴流场的尺度效应”。过去，由于船型更瘦更短，因此由伴流场的尺度效应所带来的问题并不突出。但随着大方形系数船舶和超级油轮的诞生，伴流场的尺度效应使得模型与实船之间的空化、激振力、噪声以及推进性能产生了显著差异［2］。

为了适应现代造船业的发展，满足日益增长的未来海运、海战的需要，缩短与国外先进水平的差距，国内众多学者针对尺度效应展开了研究。黄家彬等［3］通过计算某集装箱船在不同尺度下的尾流场，讨论了尺度效应对艉部平均轴向速度场的影响，试验中采用数值计算求解船艉速度和伴流场，对不同缩尺比模型的轴向伴流、伴流峰宽度和伴流等值图等参数进行了比较，对尺度伴流修正意义重大。王展智等［4］对不考虑自由液面效应的4 000 TEU以及DTMB 5415的标称伴流场进行研究，采用RANS方法对多种尺度下的粘性绕流场进行数值计算，详细研究标称伴流场的尺度效应，并重点探讨标称伴流场的各特性与雷诺数之间的定量关系，提出了一种将模型伴流场换算至实尺度的外插方法。郭春雨等［5］利用软件STAR-CCM+对不同尺度的KCS船模进行伴流场模拟，同时基于“智能假体”的概念对KCS船艉进行收缩变形处理，分析了船艉变形与伴流场尺度效应之间的关系，试验结果对于研究标称伴流的尺度效应有着重要意义。张恒等［6］以KCS船为研究对象，利用CFD软件对不同雷诺数下的船艉流场分布进行了分析，通过对比计算值与试验值发现，两者阻力系数相差不大，船艉速度场也基本吻合。

本文将对不考虑自由液面效应的KCS船的粘性绕流场进行研究，采用RANS方法和SSTk-ω模型对包含实尺度在内的不同尺度下的粘性绕流场进行数值求解，并在哈尔滨工程大学的船模水池实验室对缩尺比λ=52.667的模型进行基于PIV的标称伴流场测量试验：首先，将数值计算结果与试验数据进行对比，用以验证本文所采用数值计算方法的正确性；然后，进一步对标称伴流场的尺度效应进行详细分析。

1 数学模型

1.1 计算模型及主要参数

KCS是由韩国KRISO研究所（Korea Research Institute of Ships and Ocean Engineering）设计建造的3 600 TEU型集装箱船，在以往各届国际水动力研讨会议上，该船都被选作基准船型。可见，该船具备足够的试验数据和大量各单位提供的数值计算结果，能为本文的校核计算结果提供参考数据。KCS船舶模型如图1所示，KCS船的主尺度可参见文献［7-8］。

图1 KCS船舶模型Fig.1 Ship model of KCS

为了对标称伴流场的尺度效应进行数值研究，本文以KCS集装箱船为研究对象，对一系列不考虑自由液面、升沉和纵倾的缩尺比模型进行了数值求解。对应的傅汝德数为0.28，运动粘性系数ν=1.139 0×10-6m2/s。由于船模的主尺度不同，因此划分网格时所使用的参数及网格数量也存在着差异，各缩尺比模型的计算状态如表1所示。表中：λ为缩尺比；Lpp为垂线间长；V为船舶航速；Re为雷诺数；y+为近壁面第1层网格无量纲距离；Δy为第1层边界层厚度。

1.2 网格划分及湍流模型

首先，对船舶模型进行面网格重构（Surface remesher），对船舶表面网格进行处理并生成表面三角化良好的高质量面网格，然后以面网格为基础生成带有边界层（Prism layer mesh）和切割体网格（Trimmed mesh）的体网格。网格分布如图2所示。

本文使用的湍流模型为SSTk-ω模型，其全称为剪切应力输运（Shear Stress Transport）k-ω模型。在近壁区，使用经Wilox［9］修正过的k-ω模型，边界层以外的自由剪切流则使用k-ε模型，2种模型间的过渡应用一种混合函数完成，适用于不可压缩状态及可压缩状态。有关SSTk-ω湍流模型详见文献［10-11］。

表1 KCS不同缩尺比模型的计算参数Table 1 Computational parameters of different KCS models

图2 网格划分形式Fig.2 Mesh division technology

2 计算结果与分析

2.1 桨盘面平均轴向伴流分数尺度效应分析

当缩尺比λ=52.667时，桨盘面处无量纲轴向速度的计算值与试验值的比较如图3所示，其中左侧为试验数据，右侧为数值模拟数据。图中，Vx/V0为伴流分数w(w=1-Vx/V0)的分布情况。

由图3可以看出，数值模拟结果与试验数据符合较好［12-13］，但由数值模拟所得到的伴流场比PIV试验测量所得到的更加光顺、均匀。这说明本文所采用的网格划分方法和数值计算方法适合研究KCS集装箱船的标称伴流场，且在数值模拟中不用考虑自由液面的影响［14-15］。

图3 标称伴流场的模拟值与试验值对比Fig.3 Comparison between simulated values and experimental values of nominal wake field

不同缩尺比下的平均轴向伴流分数如表2所示。平均轴向伴流分数随雷诺数对数变化的关系如图4所示。平均轴向伴流分数的倒数随雷诺数对数变化的关系如图5所示。

由图4可以看出，各半径处平均轴向伴流分数随雷诺数对数的变化趋势较为一致。低雷诺数时，平均轴向伴流分数随雷诺数的变化较大，尺度效应明显；但随着雷诺数的变大，平均轴向伴流分数随雷诺数对数的变化趋于平缓，尺度效应问题开始变得不突出。当雷诺数大于109时，桨盘面各半径处的平均轴向伴流分数随雷诺数几乎不再变化；另外，随着半径的增大，平均轴向伴流分数迅速减小，平均轴向伴流分数随雷诺数的变化趋于平缓，表明桨盘面处内半径处的平均轴向伴流分数尺度效应问题比外半径处的更为严重。由图5可以发现，在各个半径处，平均轴向伴流分数的倒数与雷诺数的对数在中、外半径处呈近似分段线性关系。从斜率上看，平均轴向伴流分数的倒数随雷诺数对数的变化关系分为3个阶段，这3段的斜率是依次减小的，表明尺度效应问题也经历着从“严重”到趋于“缓和”的3个阶段。

表2 不同缩尺比下的平均轴向伴流分数Table 2 Mean axial wake fractions with different scale ratios

图4 各半径处平均轴向伴流分数与雷诺数的关系Fig.4 Relationship of mean axial wake fractions and Reynolds numbers at different radii

图5 各半径处平均轴向伴流分数倒数与雷诺数关系Fig.5 Relationship of reciprocal of mean axial wake fractions and Reynolds numbers at different radii

2.2 轴向标称伴流场的尺度效应分析

本节将进一步分析轴向标称伴流场随雷诺数的变化。船体绕流流动的重点考察对象为船体尾部边界层和近尾流，由于桨盘面处的速度场是螺旋桨的进流，所以研究桨盘面处的伴流场就显得尤为重要。不同缩尺比下桨盘面处的无量纲轴向速度云图如图6所示（图中实线为螺旋桨半径，虚线则分别为1.1倍和0.6倍的螺旋桨半径）。

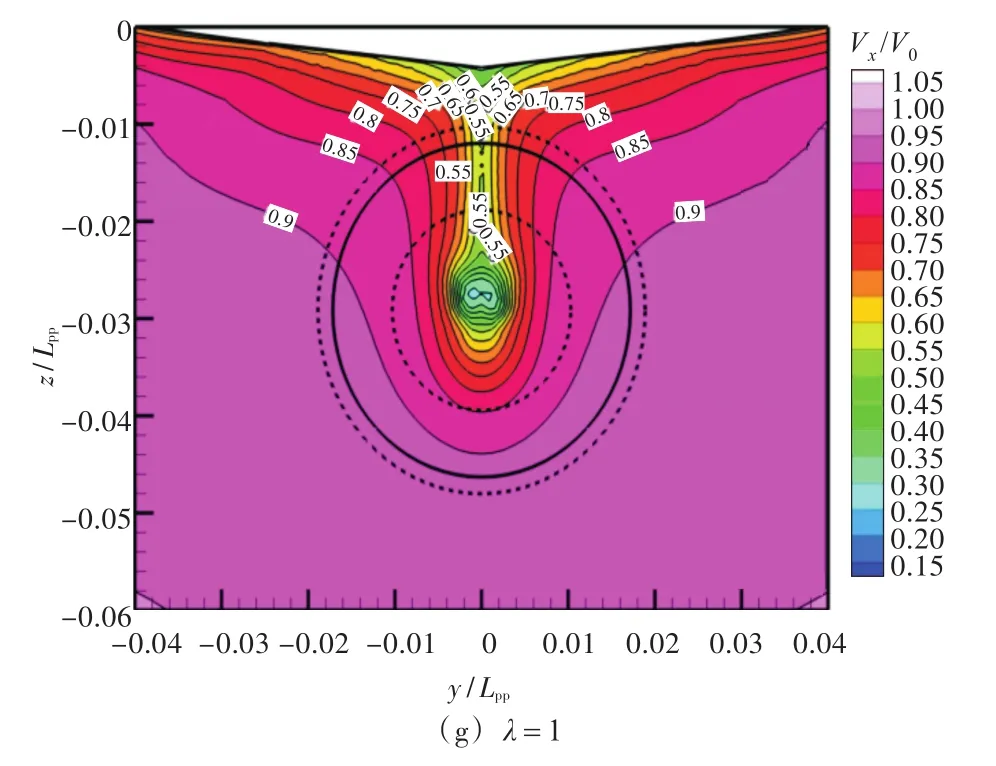
图6 不同缩尺比下桨盘面处的轴向标称伴流分布Fig.6 Distribution of axial nominal wake on propeller at different scale ratios

由图6可以看出：从模型尺度到实尺度，随着雷诺数的增加，速度边界层的厚度逐渐减小，舭部附近的边界层最厚；轴向速度等值线逐渐向螺旋桨盘面中心收缩，部分轴向速度等值线经历了向中心收缩、断裂、甚至消失的过程，这种收缩效应与Sasajima等［16］和Schuiling等［17］关于伴流换算方法的基本思想一致；随着雷诺数的增加，伴流分数变化的梯度有所降低，桨盘面处的伴流场将变得更加均匀。可见，直接应用船模尺度的标称伴流场作为螺旋桨适伴流设计的依据，所预报结果的精度并不十分可靠，必须要考虑尺度效应对其的影响。

不同缩尺比下桨盘面处轴向伴流分数的周向分布如图7所示。图中，0°指桨盘面正上方位置，而正方向是从船艉向船艏看的顺时针方向。为了更加清晰地显示伴流的形式，还对伴流分布进行了额外的一个周期延拓。

由图7可以看出，KCS船桨盘面处轴向伴流分数的周向分布总体呈“W”型。尾流场在一个周期内有2个伴流峰，一个是角位置为0°处，另一个是角位置为180°处。随着雷诺数的增加，伴流峰值逐渐减小，这对于大尺度的船模，对空泡和激振力都是有利的。在内半径区域在角位置为180°的伴流峰值处，会出现“V”型分布，这种“V”型分布在r/R=0.3处最为明显，在r/R=0.6处彻底消失。“V”型分布与雷诺数的大小也有关系，在“V”型分布最为明显的r/R=0.3处，出现“V”型分布的缩尺比为λ=52.667，31.599，16，8，当λ=4时“V”型分布已不明显，此时雷诺数应不超过λ=4时的雷诺数，由表1可得相对应的雷诺数Re≤3.1×108；而在r/R=0.6处，“V”型分布已不明显，此时对应的缩尺比λ=52.667，由表1可得相对应的雷诺数Re≤6.5×106。

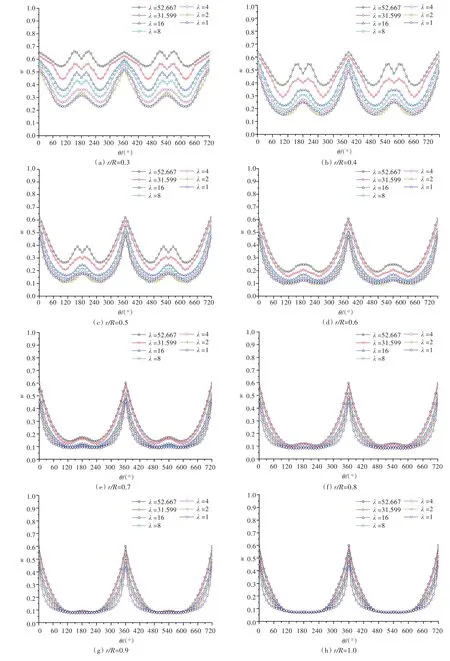
图7 不同缩尺比下桨盘面轴向伴流分数的周向分布Fig.7 Circumferential distribution of axial wake fraction on propeller at different scale ratios

3 结 语

本文采用RANS方法，结合SSTk-ω湍流模型研究了KCS标称伴流场的尺度效应，得到以下主要结论：

1）在各半径处，平均轴向伴流分数的倒数与雷诺数的对数呈正相关，和大尺度模型相比，小尺度模型的尺度效应更为明显，且在内半径处平均轴向伴流分数的尺度效应问题比外半径处的更为严重。

2）随着雷诺数的增加，边界层的厚度逐渐减小，轴向速度等值线逐渐向桨盘面中心收缩，伴流分数变化的梯度降低，伴流场将变得更加均匀。

3）桨盘面处标称伴流场的2个伴流峰分别处于正上方和正下方位置，伴流峰值会随雷诺数的增加而减小，这将有利于螺旋桨的空泡和激振力。

4）桨盘面处轴向伴流分数的周向分布总体呈“W”型，在180°位置会出现“V”型分布，但随着半径和雷诺数的增大，这种“V”型分布会更加不明显，直至消失。

［1］ LEE J H，LEE K J，PARK H G，et al.Possibility of air-filled rubber membrane for reducing hull exciting pressure induced by propeller cavitation［J］.Ocean Engineering，2015，103：160-170.

［2］ 许晶，周连第，高秋新.标称伴流尺度效应的数值模拟［J］.水动力学研究与进展，1998，13（4）：481-490. XU J，ZHOU L D，GAO Q X.Numerical simulation of scale effect on nominal wake［J］.Journal of Hydrodynamics，1998，13（4）：481-490（in Chinese）.

［3］ 黄家彬，陈霞萍，朱仁传，等.基于CFD的标称伴流场尺度效应研究［C］//第九届全国水动力学学术会议暨第二十二届全国水动力学研讨会论文集.北京：中国力学学会，2009.

［4］ 王展智，熊鹰，黄政，等.双桨船轴向伴流场尺度效应的数值研究［J］.上海交通大学学报，2015，49（4）：457-463. WANG Z Z，XIONG Y，HUANG Z，et al.Numerical study on scale effect of axial wake of twin screw ship［J］.Journal of Shanghai Jiaotong University，2015，49（4）：457-463（in Chinese）.

［5］ 郭春雨，张琪，陈鸽，等.基于SDM方法的船艉伴流场尺度效应研究与修正［J］.中国舰船研究，2015，10（6）：1-7. GUO C Y，ZHANG Q，CHEN G，et al.Research and revision on the scale effect of the wake field based on the method ofSDM［J］.Chinese Journal Ship Research，2015，10（6）：1-7（in Chinese）.

［6］ 张恒，詹成胜，刘祖源，等.基于船舶阻力性能的船型主尺度参数敏感度分析［J］.船舶工程，2015，37（6）：11-14. ZHANG H，ZHAN C S，LIU Z Y，et al.Analysis of sensitivity of ship type main dimension parameters based on ship resistance performance［J］.Ship Engineering，2015，37（6）：11-14（in Chinese）.

［7］ SHEN Z R，WAN D C，CARRICA P M.Dynamic overset grids in OpenFOAM with application to KCS self-propulsion and maneuvering ［J］. Ocean Engineering，2015，108：287-306.

［8］ FUJISAWA J，UKON Y，KUME K，et al.Local velocity field measurements around the KCS model（SRI M.S. No.631） in the SRI400 mtowing tank：ship performance division report：00-003-02［R］.［S.l.］：Ship Research Institute，2000.

［9］ WILOX D C.Turbulence modeling for CFD［M］.La Canada，California：DCW Industries，Inc.，1998.

［10］ SHIH T H，LIOU W W，SHABBIR A，et al.A newk-εeddy viscosity model for high Reynolds number turbulent flows［J］.Computers&Fluids，1995，24（3）：227-238.

［11］ MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications［J］. AIAA Journal，1994，32（8）：1598-1605.

［12］ KIM W J，VAN S H，KIM D H.Measurement of flows around modern commercial ship models［J］. Experiments in Fluids，2001，31（5）：567-578.

［13］ YANG H U，KIM B N，YOO J H，et al.Wake comparison between model and full scale ships using CFD［J］.Journal of the Society of Naval Architects of Korea，2010，47（2）：150-162.

［14］ WANG Z Z，XIONG Y，WANG R，et al.Numerical study on scale effect of nominal wake of single screw ship［J］.Ocean Engineering，2015，104：437-451.

［15］ KIM D，LEE K，SEONG W.Non-cavitating propeller noise modeling and inversion［J］.Journal of Sound and Vibration，2014，333（24）：6424-6437.

［16］ SASAJIMA H，TANAKA I.On the estimation of wakes of ships［C］//Proceedings of 11th ITTC.Tokyo，Japan：ITTC，1966：140-144.

［17］ SCHUILING B，LAFEBER F H，VAN DER PLOEG A，et al.The influence of the wake scale effect on the prediction of hull pressures due to cavitating propellers ［C］//Proceedings of the Second International Symposium on Marine Propulsors. Hamburg，Germany：［s.n.］，2011.

Numerical analysis of the scale effect of the nominal wake field of KCS

ZHANG Haipeng，ZHANG Donghan，GUO Chunyu，WANG Lianzhou，LIU Tian
School of Shipbuilding Engineering，Harbin Engineering University，Harbin 150001，China

In order to study the scale effect of the nominal wake field,the viscous flow field of KCS is studied without considering the free surface effect,and the nominal wake fields of KCS at different scales including full scale are solved numerically using the RANS method and the SSTk-ωturbulence model. By comprehensively comparing the computed results with experimental data,the scale effect of the nominal wake field is further investigated.This shows that the reciprocal of the mean axial wake fraction at each radius exhibits a near-linear dependence on the Reynolds number in a logarithmic scale;for the nominal wake field of the propeller disc of KCS without a propeller,two wake peaks exit,and the amplitude of the axial wake peak decreases with the increase of the Reynolds number,which is conducive to a decrease in propeller exciting force and propeller cavitation;the scale effect of the small scale model is more obvious, and the scale effect of the mean axial wake fraction in the inner area is stronger than it is in the outer area.

nominal wake field；scale effect；KCS；numerical calculation

U661.1

A

10.3969/j.issn.1673-3185.2017.01.001

2016-07-05

2016-12-28 16:06

国家自然科学基金资助项目（51209048，41176074，51409063）；工信部高技术船舶科研资助项目（G014613002）；哈尔滨工程大学青年骨干教师支持计划（HEUCFQ1408）

张海鹏，男，1981年生，博士，讲师。研究方向：反步控制法及其在减摇鳍中的应用。E-mail：hpzhangheu@126.com张东汗（通信作者），男，1993年生，硕士生。研究方向：近自由面物体绕流。E-mail：740068735@qq.com郭春雨，男，1981年生，博士，教授。研究方向：船舶推进性能与节能，船舶流体力学实验技术。E-mail：guochunyu@hrbeu.edu.cn

http://www.cnki.net/kcms/detail/42.1755.TJ.20161228.1606.040.html期刊网址：www.ship-research.com

张海鹏，张东汗，郭春雨，等.KCS标称伴流场的尺度效应数值分析［J］.中国舰船研究，2017，12（1）：1-7. ZHANG H P，ZHANG D H，GUO C Y，et al.Numerical analysis of the scale effect of the nominal wake field of KCS［J］. Chinese Journal of Ship Research，2017，12（1）：1-7.