解常微分方程程序的蜕变测试方法*

邱舒婷 张志祥

(海军工程大学计算机工程系 武汉 430033)

解常微分方程程序的蜕变测试方法*

邱舒婷 张志祥

(海军工程大学计算机工程系 武汉 430033)

数值计算方法被广泛运用于实际生活中,解微分方程问题则是数值计算问题中的一个重要分支,但由于求解微分方程的程序很难直接找到一个测试Oracle来验证程序的有效性,进而提出用蜕变测试方法检测解微分方程程序的有效性。通过对解常微分方程的典型程序测试的案例分析,提出了一种求解常微分方程程序的蜕变测试方法,最后进行一个实例验证该方法的有效性。

数值计算;微分方程;蜕变测试;Oracle问题

(Department of Computer Engineering, Naval University of Engineering, Wuhan 430033)

Class Number TP311

1 引言

数值计算程序对我们的日常生活非常重要,不仅广泛运用于各种理论学科中,还在动力工程和医学实践中的任务关键型和安全关键型应用中有所体现。

由于数值计算中一些不可避免的截断误差,取整误差以及计算进程中的传播误差会影响到最终结果,并且找不到一种确切的解法来解决这个问题,因此在很多情况下,测试人员很难甚至是不能得出程序的预期输出,进而无法将程序的输出结果与预期结果相比较,这就是软件测试中常说的Oracle问题[2]。据此,人们提出三种测试方法来为数值计算程序提供一个可选的Oracle[1]：

1) 静态检查,进行代码走查检验程序。

2) 动态执行,比较不同的数值计算程序生成的结果。

3) 利用不同的参数设置和输出结果的一致性来运行该软件。

运用代码走查的方法检验程序只适用于程序代码量并不多的情况,但在复杂程序中此法效率很低。即使可以检测到一些数值解和实验结果之间的差异,也很难去验证它们是由于程序bug还是在物理建模中的错误引起的。并且在实际情况中,不同的环境设置可能会导致不同的结果。为解决这种Oracle问题,Chen等提出了蜕变测试技术[1]。

在运用蜕变测试技术解决数值计算软件测试中遇到的Oracle问题上,Tse T H等利用网格精度的不同对偏微分方程程序的执行结果有不同的影响构造出一条蜕变关系,测试了一个狄利克雷边界条件下的椭圆型偏微分方程程序[3],实验表明网格精度越高,暴露出程序错误的可能性越大,但在不同网格精度中产生的相对误差值也十分近似,因此适用范围较为局限。

姚奕等利用蜕变测试技术求解直角坐标系上的图形面积来对面向整数错误检测的蜕变测试方法进行实例研究[4]。测试发现由于整型错误产生的隐错,实验结果显示基于蜕变关系的整型错误检测方法可检测出平时发现不了的隐式非预期输出,有效地提高了检测整型错误的效率[11]。

由此可见,相较于一般的测试方法,蜕变测试技术在数值计算软件测试中能够更有效地检验复杂数值计算程序的正确性。

在数值计算问题的众多分支中,微分方程数值解法占有重要的地位。它以数值代数和逼近论等学科为基础,并反过来推动这些相关学科的发展,在科学计算、工程技术等领域有着极其广泛的运用[5]。但微分方程的数值解法根据微分方程的不同类别各不相同,且很难直接得出其预期结果,而蜕变测试技术在测试微分方程数值计算程序中运用还不是很广泛,本文将研究用蜕变测试(Metamorphic Testing,MT)技术来缓解数值计算程序中的Oracle问题。

2 相关定义

2.1 蜕变测试相关定义

定义1 蜕变关系(Metamorphic Relation,MR)。假设程序P是用于计算函数f的,f：X→Y在定义域为X,值域为Y上的函数。假设f满足关系Rf,且关系Rf满足当f的n组输入为x1,x2,…,xn∈X(n>1)时,对应的一系列函数输入结果分别为f(x1),f(x2),…,f(xn)∈Y。这种关系Rf称为关于f的一条蜕变关系。因此,若程序P是正确的,那么它一定满足推导式(1)：

R(I1,I2,…,In) =Rf(P(I1),P(I2),…,P(In))

(1)

式中：I1,I2,…,In是程序P对应于x1,x2,…,xn的实际输入,P(I1),P(I2),…,P(In)则是对应的输出结果。

以正切函数为例。对于任意两个输入x1和x2,满足x2=π+x1时,一定有tanx2=tanx1。这种关系即可视为一条蜕变关系：

Rtan：x2=π+x1→tanx2=tanx1

(2)

因此在进行测试时,可通过验证式(1)、(2)的成立与否来验证程序P的输出结果正确与否。

定义2 蜕变测试(Metamorphic Testing,MT)。蜕变测试是一种利用未暴露程序错误的成功测试用例衍生出后续测试用例,并用衍生测试用例验证是否满足程序的某些必要属性来判断程序正确性的技术。

测试人员通常会先在原始程序中植入一个变异,再利用蜕变关系生成衍生测试用例进行程序测试。若程序未支持在该蜕变关系下应满足的属性,则说明程序存在变异[8]。

2.2 常微分方程的数值计算

定义3 龙格库塔法(Runge-Kutta)：龙格库塔法[6]是一种在工程上应用广泛的高精度单步算法,用于数值求解微分方程。对于一阶精度的拉格朗日中值定理有：

对于微分方程：y′=f(x,y)即y(i+1)=y(i)+h*k1,k1=f(xi+yi)。

当用点xi处的斜率近似值k1与右端点xi+1处的斜率k2的算术平均值作为平均斜率k*的近似值,那么就会得到二阶精度的改进拉格朗日中值定理：

y(i+1)=y(i)+[h*(k1+k2)/2]

k1=f(xi+yi)

k2=f(x(i)+h,y(i)+h*k1)

依次类推,如果在区间[xi,xi+1]内多预估几个点上的斜率值k1,k2,…,km,(m>1)并用它们的加权平均数作为平均斜率k*的近似值,显然能构造出具有很高精度的高阶计算公式。经数学推导与求解,可以得出四阶龙格库塔公式,也就是在工程中应用广泛的经典龙格库塔算法：

y(i+1)=y(i)+[h*(k1+2*k2+2*k3+k4)/6]
k2=f(x(i)+h/2,y(i)+h*k1/2)
k3=f(x(i)+h/2,y(i)+h*k2/2)
k4=f(x(i)+h,y(i)+h*k3)

2.3 常微分方程求解示例

在实际工作中,解决一项现实问题需要成千上万个微分方程组,人工求解微分方程的通解是很不现实的,所以微分方程的数值解显得尤为重要。

在此以一个一阶非线性常微分方程(3)为例,给出初始条件当x0=1时,y0=1且x∈[1,6]。

(3)

假设用“四阶龙格库塔法”解上述常微分方程问题。在给定边界条件和步长h的情况下,程序可以计算出每隔h步长后的x和y的值直到迭代结束[7]。为说明蜕变测试的有效性,我们会在解常微分方程的程序中植入一个变异。图1是原始程序的关键代码。

图1 关键代码图

假设通过将上述程序中的第7行代码:

k2=(*pfunc)(x0+h/2,y0+k1*h/2)

替换为：

k2=(*pfunc)(x0+h/2,y0-k1*h/2)

来植入一个变异[10],并将设计的该变异程序版本记为Mutant1。将上述原始和植入错误的程序编译执行后,得到的运行结果趋势如图2所示。

图2 非线性原始和变异程序运行结果图

从上述原始和植入变异过后的程序结果中可以看出,两个程序的输出值几乎重合,说明两个程序的运行结果十分相似。随着x值的逐步增大,y值逐渐递减,且最终的y100值变异的运行结果和原始结果相差甚微。因此,当这种问题出现在实际应用中时,我们就很难发现错误的存在。

3 解一阶非线性常微分方程的蜕变测试方法

由于无法通过一般运算求得一阶非线性常微分方程的通解,进而无法构造出程序的预期输出,待测程序缺乏测试Oracle,因此直接检测出程序中是否存在错误是有一定难度的。

通常在一般的一阶常微分方程求解问题中,讨论一阶非线性常微分方程u′=f(t,u)的绝对稳定性*绝对稳定性：不管在理论还是应用方面,单步法和多步法都必须是稳定的。但这种稳定有两方面的限制：一是要求h∈(0,h0)充分小,而实际用的h∈(0,h0)都是固定的；二是只允许初值有误差,往后各步计算都精确,而实际计算时每步都可能有舍入误差,为了控制这种误差的增长,需对多步法提出进一步要求,即绝对稳定性。非常困难,因而通常考虑它在解u临近的线性化方程,即简化成讨论一种简单的线性常微分方程u′=a*u的绝对稳定性,其中a为实数或复数。

由此引申,由于在用蜕变测试检测程序的有效性时,检测一阶非线性常微分方程u′=f(t,u)的有效性难度很大,同样可以考虑检测u临近的线性化方程u′=a*u的有效性。为解决上述无法检测出原始程序中的变异问题,提出基于检测一阶非线性微分方程有效性的蜕变测试一般方法,如图3所示。

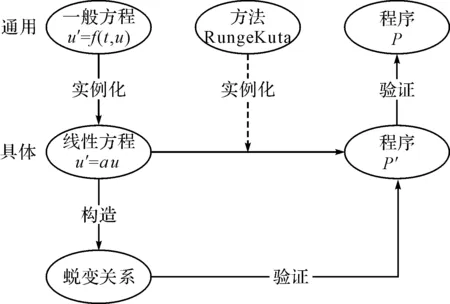
图3 基于一阶非线性微分方程的蜕变测试一般方法

蜕变检测一阶非线性常微分方程的一般方法步骤描述如下：

1) 对于一个一般的一阶非线性常微分方程y′=f(x,y),必定存在一个解该方程的一般方法Runge-Kuta,此处以四阶龙格库塔法为例,将方法Runge-Kuta对应的解一阶非线性常微分方程程序记为P。

2) 实例化一阶非线性常微分方程y′=f(x,y),简化后的方程为一阶线性常微分方程,记为y′=a*y(a为实数或复数)。方程y′=a*y对应的Runge-Kuta法记为Runge-Kuta1,对应的实现Runge-Kuta1法解一阶线性常微分方程的程序记为P’。

3) 对一阶线性常微分方程y′=a*y构造蜕变关系MRi(i=1,2,3…),用MRi验证实例化的程序P’,若程序P’存在错误,则可推断原始程序P中存在错误。

4 一阶非线性常微分方程蜕变测试实例

4.1 实例化一阶非线性常微分方程

对于一个解一阶非线性微分方程y′=f(x,y)的程序P,直接检测出其中是否存在错误是有一定难度的。若能在其对应的解实例化后的一阶线性微分方程y′=g(x,y)的程序P′中检测出变异的存在,则能证明原始程序P的算法是有错误的。

因此,将原始的非线性函数f(x,y)=-x*y2实例化为一个线性函数g(x,y)=u*y,作为程序的初始函数。令u=-3,此时实例化后的新微分方程记为一阶线性微分方程(4)

(4)

同样在程序中植入变异Mutant1,将上述实例化后的解一阶线性微分方程的原始和植入错误的程序编译执行后,得到的运行结果趋势如图5所示。

图4 线性原始和变异运行结果图

遗憾的是,从以上两个程序运行结果中依旧只能发现与图2即最初的常微分方程程序运行结果类似的规律,即随着x值的逐步增大,y值依旧在逐渐递减,且最终的y100值在变异后程序中的运行结果与原始程序的运行结果均近似为0(由于程序中数值精度有限,计算结果存在一定的误差)。进而说明,通过将微分方程实例化到一个相对简单的一阶线性常微分方程上,是不足以验证原始的解一阶非线性微分方程程序是否存在错误的。

4.2 解一阶线性微分方程程序的蜕变测试方法

4.2.1 蜕变关系的构造

通过对一阶线性微分方程(4)构造蜕变关系来验证一阶线性常微分方程程序的正确性,进而分析原始程序是否存在错误。一阶线性常微分方程(4)可表达为

(5)

解方程(5)的程序记为被测程序P′。根据一阶线性微分方程的一般数值求解方法,可得出式(5)的通解为

y=e3*e-3x,c=e3

(6)

根据式(6)的性质,可以构造出以下蜕变关系,如图5所示。

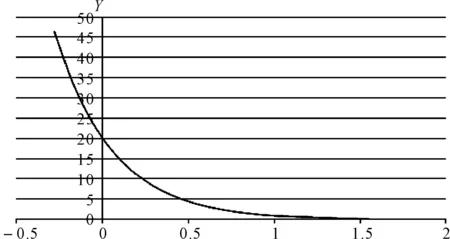
图5 y=e3*e-3x函数图像

在上图中可以看出随着x值的逐渐增大,y值是单调递减的,且y值始终大于0。根据这一条性质,可以构造蜕变关系1,记为MR1。则MR1可描述为

MR1：∀i,j∈且iy(xj)>0。

当x取它的相反数-x时,此时对应的函数为y=e3*e3x,函数y与y’关于y轴对称,且存在恒等式y(xk)*y(-xk)=e6。根据这一条性质,可以构造出蜕变关系2,记为MR2。则MR2可描述为

MR2：∀k∈,y(xk)*y(-xk)=e6。

以上两条蜕变关系MR1,MR2就是测试执行被测程序P’的所用到的蜕变关系。若程序执行结果未满足以上的关系,就有充分的理由断定被测程序P’存在错误。

4.2.2 测试结果

根据MR1和MR2在Windows环境下使用VC++编译器执行变异程序,选取程序的部分运行结果如表1所示。其中最后一列的yx*y-x为由蜕变关系MR2构造的衍生测试用例。

从表1中可以看出,对于任意逐渐增大的x值,y值始终在不断递减且y>0。因此蜕变关系MR1检测不到程序的任何错误。而在最后一列yx*y-x中,yx*y-x的值很明显不等于e6,因此利用蜕变关系MR2,检测出了解一阶线性常微分方程的程序存在异常,即蜕变关系MR2的检错能力大大高于蜕变关系MR1。这是由于MR2的输入变换约束力更强,较MR1更为复杂,与“优先考虑输入的蜕变关系表达式较复杂一方”的原则一致[9]。实验证明原始的解一阶非线性常微分方程的程序存在异常,程序版本Mutant1存在缺陷。

表1 测试执行结果

5 结语

因为缺少分析方法,大多数微分方程通常通过数值方法解决。由于如前面章节所说的种种原因,对于这样的数值方法可能不存在测试Oracle。而将微分方程简化并聚焦到一阶线性常微分方程问题上,会有助于解决一些问题,但是还不足以暴露出一些细微的错误,比如本文中所描述的错误。相反的,我们在简化的方程的基础上确定了蜕变关系并进行了蜕变测试,然后设法从程序中找出问题所在。

本文以一阶线性常微分方程为例,总结了蜕变测试是如何帮助减少数值计算软件测试中的Oracle问题,并通过实验证明利用蜕变关系的构造可以检测出微分方程程序中的一些细微问题,在未来的更深入的微分方程的应用中我们可以得到进一步的钻研。

[1] Chen T Y,Cheung S C,Yiu S M.Metamorphi-c testing：A new approach for generating next test cases[R].HKUST-CS98-01.Hong Kong,1998.

[2] Chen T Y,Huang D H,Tse T H,et al.Case studies on the selection of useful relations in metamorphic testing[C]// Symposium on Software Engineering&Knowledge Engineering.Madrid,Spain,2004：569-583.

[3] Chen T,Feng T H,Tse.Metamorphic testing of programs on partial differential equations：a case study[C]// Proceedings of the 26th Annual International Computer Software and Applications Conference. Baltimore,Marriott,USA,2002：327-333.

[4] 姚奕,黄松,稽孟雨.面向整数错误检测的蜕变测试方法研究[J].计算机工程与科学,2012：52-56.

[5] 李荣华,刘博.微分方程数值解法[M].第四版.北京：高等教育出版社,2009：38-41.

[6] Khodabin M,Rostami M.Mean square numerical solution of stochastic differential equations by fourth order Runge-Kutta method and its application in the electric circuits with noise[J]. Advances in Difference Equations,2015：3-19.

[7] Chapra S C and Canale R P.Numerical Methods for Engineers：with Software and Programming Applications[M].New York：McGraw-Hill,2002.

[8] Offutt A J,Rothermel G,Zapf C.An experime-ntal evaluation of selective mutation[C]// Proceedings of the Fifteenth International Conference on Software Engineering.IEEE Computer Society,Washington DC,2003：100-107.

[9] Dong G W,Nie C H,Xu B W,et al.An effective iterative metamorphic testing algorithm based on program path analysis[C]//Proceedings of the 7th Annual International Conference on Quality Software.IEEE Computer Society,Washington DC,2007：292-297.

[10] WU Peng,SHI Xiao-Chun,TANG Jiang-Jun,et al.Metamorphic Testing and Special Case Testing:A Case Study[J]. Journal of Software,2005：1210-1214.

[11] Manolache L I,Kourie D G.Software Testing Using Model Programs[J].Software Practice and Experience,2001,31(13)：1211-1236.

版 权 声 明

本刊已许可万方数据库、中国学术期刊(光盘版)电子杂志社在中国知网及其系列数据库等产品中以数字化方式复制、汇编、发行、信息网络传播本刊全文。著作权使用费与本刊稿酬一并支付。作者向本刊提交文章发表的行为即视为同意我编辑部上述声明。

《舰船电子工程》编辑部

Metamorphic Testing of Ordinary Differential Equations Program

QIU Shuting ZHANG Zhixiang

Numerical methods are widely used in our real life, solving differential equations is an important branch of numerical problems. But it is difficult to find a test Oracle to verify the effectiveness of programs which solving differential equations. In this paper, metamorphic testing method is used to detect the effectiveness of the program which used to solve differential equations. Through analyzing the case of a typical program case, we propose the metamorphic test method of solving ordinary differential equations. At last, an instance is verified to illustrate the validity of this method.

numerical calculation, differential equations, metamorphic testing, Oracle problem

2016年6月9日,

2016年7月25日

邱舒婷,女,硕士研究生,研究方向:软件质量保证技术。张志祥,男,副教授,硕士生导师,研究方向:程序设计方法,软件工程等。

TP311

10.3969/j.issn.1672-9730.2016.12.007