浅谈概率学习中的问题成因与解决策略
于良

[摘 要] 概率问题作为中考的常见题型之一,看似容易,实则蕴含深远. 学生由于缺乏对这一问题的数学史方面的知识渗透,难免对此类问题有许多把握不到位的地方. 本文以概率学习中的常见问题为抓手,细致分析了这些问题的成因,找出了解决这些问题的常见对策.
[关键词] 概率学习;问题成因;解决对策
概率是中考必考的知识点之一,在现在的中考中已经显得越来越重要了. 从近几年各地的中考试卷来看,概率的考试题目类型大致可分为三类:(1)利用频率值估计概率;(2)利用面积计算概率;(3)利用画树状图或列表法解决生活类实际应用问题. 这些常见的考题中间往往隐藏着一些典型的错误,教师需要借助这些错误,分析错误,纠正错误,让学生得到真正的提高. 学生在初涉概率知识时往往不会觉得很困难,可一旦遇到具体问题,却时常出错. 下面笔者就根据多年来的教学实际,对这些错误原因进行归类和总结,并找出解决这一类错误的有效方法.
对机会的等可能性理解不够导
致错误
问题1 甲、乙、丙、丁四人参加某校教师招聘考试,试后甲、乙两人去询问成绩. 评委对甲说:“恭喜你,你不是最差的,丙是最差的. ”对乙说:“四人的成绩均不相同,但可惜你未能获得第一名. ”请你根据回答的内容进行分析,这四人的名次排列共有______种不同的可能情况.
错解 不知如何作答,瞎猜一个作为标准答案.
正解 根据评委的话,可以将整个事件看成两个部分组成:①应聘者;②考试名次,将条件整理成表格形式.
由表格可知:甲的名次可能是①或②或③,乙的名次可能是②或③,丁的名次可能是①或②或③,丙为第④名,而其余三人只能是①②③中一个名次,所以所有等可能的结果为甲①乙②丙④丁③;甲③乙②丙④丁①;甲②乙③丙④丁①;甲①乙③丙④丁②. 以下列举一些学生常见的错误:(1)根据题目提供的条件多而乱,感觉无从下手,便不会处理;(2)能够确定丙的名次,但如何确定甲、乙、丁的名次没有头绪;(3)甲有3种情况,乙有2种情况,丁有3种情况,所以总共有3×2×3=18种情况;(4)漏掉考虑甲③乙②丙④丁①和甲②乙③丙④丁①这两种情况.
归因与剖析 在确定等可能结果时,首先要弄清楚本题关注的是什么结果,其次结果由谁决定,接着把有关的可能情况分析清楚. 以上题为例,要求名次所有的情况,其次由于丙为第④名,所以名次只与甲、乙、丁有关,接着由题可知甲可能为①②③,乙可能为②③,丁可能为①②③,而三人只能得一个名次而不重复,便可得出答案.
对问题中有无放回的理解出现 错误
问题2 已知红色和蓝色在一起可配成紫色,现有三种颜色,即红色、白色和蓝色,从中任意取出两种颜色来配紫色,问:能配出紫色的概率有多大?
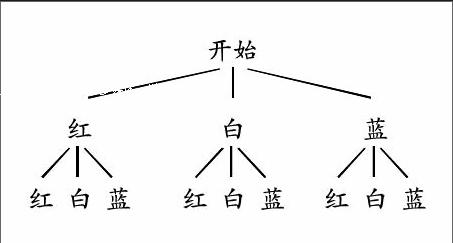
错解 画树状图:
所有等可能的结果共有9种,其中配出紫色的结果有2种,P(配出紫色)=.
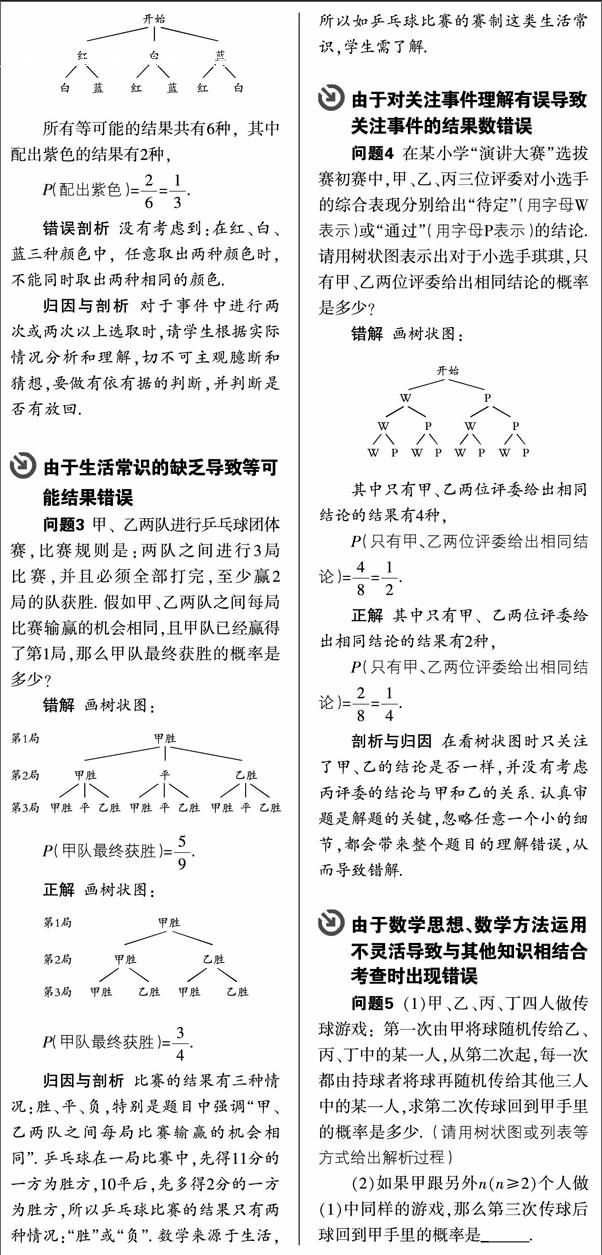
正解 画树状图:
所有等可能的结果共有6种,其中配出紫色的结果有2种,
P(配出紫色)==.
错误剖析 没有考虑到:在红、白、蓝三种颜色中,任意取出两种颜色时,不能同时取出两种相同的颜色.
归因与剖析 对于事件中进行两次或两次以上选取时,请学生根据实际情况分析和理解,切不可主观臆断和猜想,要做有依有据的判断,并判断是否有放回.
由于生活常识的缺乏导致等可 能结果错误
问题3 甲、乙两队进行乒乓球团体赛,比赛规则是:两队之间进行3局比赛,并且必须全部打完,至少赢2局的队获胜. 假如甲、乙两队之间每局比赛输赢的机会相同,且甲队已经赢得了第1局,那么甲队最终获胜的概率是多少?
错解 画树状图:
P(甲队最终获胜)=.
正解 画树状图:
P(甲队最终获胜)=.
归因与剖析 比赛的结果有三种情况:胜、平、负,特别是题目中强调“甲、乙两队之间每局比赛输赢的机会相同”. 乒乓球在一局比赛中,先得11分的一方为胜方,10平后,先多得2分的一方为胜方,所以乒乓球比赛的结果只有两种情况:“胜”或“负”. 数学来源于生活,所以如乒乓球比赛的赛制这类生活常识,学生需了解.
由于对关注事件理解有误导致
关注事件的结果数错误
问题4 在某小学“演讲大赛”选拔赛初赛中,甲、乙、丙三位评委对小选手的综合表现分别给出“待定”(用字母W表示)或“通过”(用字母P表示)的结论. 请用树状图表示出对于小选手琪琪,只有甲、乙两位评委给出相同结论的概率是多少?
错解 画树状图:
其中只有甲、乙两位评委给出相同结论的结果有4种,
P(只有甲、乙两位评委给出相同结论)==.
正解 其中只有甲、乙两位评委给出相同结论的结果有2种,
P(只有甲、乙两位评委给出相同结论)==.
剖析与归因 在看树状图时只关注了甲、乙的结论是否一样,并没有考虑丙评委的结论与甲和乙的关系. 认真审题是解题的关键,忽略任意一个小的细节,都会带来整个题目的理解错误,从而导致错解.
由于数学思想、数学方法运用
不灵活导致与其他知识相结合
考查时出现错误
问题5 (1)甲、乙、丙、丁四人做传球游戏:第一次由甲将球随机传给乙、丙、丁中的某一人,从第二次起,每一次都由持球者将球再随机传给其他三人中的某一人,求第二次传球回到甲手里的概率是多少. (请用树状图或列表等方式给出解析过程)
(2)如果甲跟另外n(n≥2)个人做(1)中同样的游戏,那么第三次传球后球回到甲手里的概率是______.
第(1)问比较容易,共有9种等可能的结果,符合条件的情况有3种, 概率为. 下面研究第(2)小问.
解法1 所有等可能的结果共有n3种,其中第三次传球后球回到甲手里的结果有n(n-1)种,P(第三次传球后球回到甲手里)==.
解法2 (画图解决)画出n=2时,三次传球后的树状图,得P===;
画出n=3时,三次传球后的树状图,得P===;
画出n=4时,三次传球后的树状图,得P===,
所以通过表示可得出该题规律为P=.
归因与剖析 从这个问题中,我们明显可以得到两点启示:①第(2)小题在考查学生“化归思想”,如果学生遇到一个题目有多个小题,且每个小题所求的结论类似时,可以尝试用第1小题的处理方式来解决之后的小题,这也是“化归思想”想考查学生的地方. ②遇到找规律的题目时,请注意处理方法:从n的最小值开始去研究题目要求的量,不要怕烦琐,直到所代入的数能从结果中发现规律为止,只要将变化部分用字母代替,不变部分照抄就能得出规律.
归纳与反思
概率是中考命题的重点之一,经常与统计、函数、几何图形等知识综合在一起考查,我们需牢固掌握树状图(列表)法,利用概率公式解决此类问题. 题目千变万化,我们需养成良好的审题习惯,善于总结归纳,力争让自己不断提高. 从五类常见错误来看,阅读和理解是第一步,只有正确地把握题目的含义,抓住阶梯的关键因素,才能有效地避免出错,而从学生的问题中,教师也能反思自身课堂的得失,找到最佳的教学方式,实现最好的课堂效果.

