初中数学语言转化能力培养也需切实切需

顾明

[摘 要] 数学是研究客观世界的一种有效工具，而数学语言是数学工具的一种显性的体现，是数学交流必不可少的媒介之一，也是一种思维的外显形式。数学语言一般包含符号语言、图形语言和文字语言三种，三种语言之间都能进行一定的转化，也存在着较强的联系，数学语言能力的强弱直接体现学生的数学学习水平，所以，培养学生的数学能力成为数学教育教学的重要点和关键点，已经被越来越多的人所认识.

[关键词] 数学语言转化；数学能力培养；数学图形语言

众所周知，数学学习是对学过的知识再加工、再深化的过程. 数学语言转化能力最佳的效果是融知识技能、思想方法、创新能力于一体，学生在定义、定理、公式、法则学习的基础之上，把原来新授课的知识点重新串联起来，形成知识体系链状结构，让学生把没有掌握到位的知识进行再加工和提炼. 数学教师创造性地组织数学教学活动，不急于抛出自己的解法观点，而是在师生阅读过程中享受“慢教育”，在“留白”中让学生通过独立思考，表达对相同问题的个人见解，虽然学生理解的程度不同，却各具特色. 在不断追求新知的过程中，学生的双基能力不断夯实，复习过程也呈现出了喜人的再发现、再创造的场面，发散彻底，聚焦到位，体验实践中结合教师追问，让学生参与试讲. 在此程度上，教师把握思维核心，立足于通法通式感知，充分发挥引导作用，使文字语言表达生动，符号语言书写方便，学习起来一目了然，图形语言表达直观，有助记忆和思维直白. 因此，在教学中，我们既要强调语义解释，又要注重句法分析.

借助文字语言的表达，加强记

忆和理解

在初一数学的学习中，我们用字母a来表示数，学生常常会认为带“+”的是正数，带“-”的是负数，错把“-a”看成负数，那么我们老师可以引导学生将“-a”这个符号语言用数学文字语言表示出来，即“a的相反数”，使学生理解“-a”可以是正数、零或负数. 如同底数幂的乘法公式am·an=am+n，它的文字语言是“同底数幂相乘，底数不变，指数相加”，这样的情况显然文字表述不如公式描述来得直观，公式更方便学生理解与记忆. 而在解决a-2+（b+3）2=0这类问题时，教师往往会利用文字表述来说明，这样会显得更加形象和生动.

文字语言准确、严谨，很多时候具有不可替代性. 在平时的教学中，我们要引导学生将一些公式、法则、结论用文字语言表述出来，这样可以加深学生对概念、知识的理解和记忆. 这样的阅读起点就是建立在学生的生活经验基础之上，让学生既感受到生活中隐藏着数学问题，又体验到能利用数学知识解释生活想象.

体会符号语言的一般性，表示

变化的规律

数学符号以其独有的浓缩形式，蕴含了大量的信息，在代数中，用字母表示数，用代数式、方程、不等式、函数等表示事物之间的关系和变化规律；在几何中，很多定义、定理都有它的符号语言表达形式. 我们解答几何题的过程就是符号语言的完美呈现过程. 《义务教育数学课程标准（2011版）》提出符号意识的概念，即符号意识主要指能够理解并且运用符号来表示数、数量关系和变化规律，旨在加强学生对数学符号语言的使用，而这种应用和理解也是建立在原来阅读理解的基础之上的. 初中阶段是数学符号语言学习的关键时期，学生通过学习数学符号语言可以体会数学的奥妙、探讨数学方法、锻炼数学思维.

问题1 如图1，一个周长为2l的长方形房间，正好被分割成2个长方形和3个正方形，五块部分成中心对称. 如果只知该住房的周长，那么分割后不通过测量就能知道周长的是下列哪块标有数字的图形？（ ）

A. ①② B. ②③

C. ①③ D. ①②③

这类题目考查学生符号语言的表达能力，同时我们也可以从中发现用符号语言来描述规律相对于用文字语言来描述要简明得多.

利用图形语言的直观，巧妙解

决问题

图形一般说来就是某事物的代号，它把复杂的事物用简便的形式表现出来. 图形语言是一种视觉语言，通过图形给出某些条件. 数学图形语言包括数学中的图像、计算机中的图画、统计中的统计图和数据表等. 我们日常教学中常用的图形语言有线段图、数轴图、集合图、单位圆、几何图等. 数学图形语言表现直观，有助记忆，有助思维，有益于问题解决. 数学图形语言对初中生学习数学知识、发展抽象思维、建立数学思想及解决一些数学问题都起着关键性的作用. 利用图形解决问题时，首先必须抓住问题的关键，探寻问题的本质.

问题2 如图3，半径为r的☉O分别绕面积相等的等边三角形、正方形和圆，用相同的速度匀速滚动一周，用时分别为t1，t2，t3，则t1，t2，t3的大小关系为______.

分析 根据面积可得相应的周长，根据有理数的大小比较，可得答案.

解答 设面积相等的等边三角形、正方形和圆的面积均为S，则等边三角形的边长a=，等边三角形的周长为3a=3；正方形的边长b=，正方形的周长为4b=4；圆的周长为2. 因为周长平方后分别为12S，16S，4πS，所以t1>t2>t3，故答案为t1>t2>t3.

数学三种语言有机结合带来

的便利

对于很多几何问题，一开始往往是用文字叙述的，后来逐渐直观化作出对应的图形，这在阅读上面就显得一目了然，便于学生学习和理解. 下面我们以问题3为例，分析一下三种语言综合使用的问题.

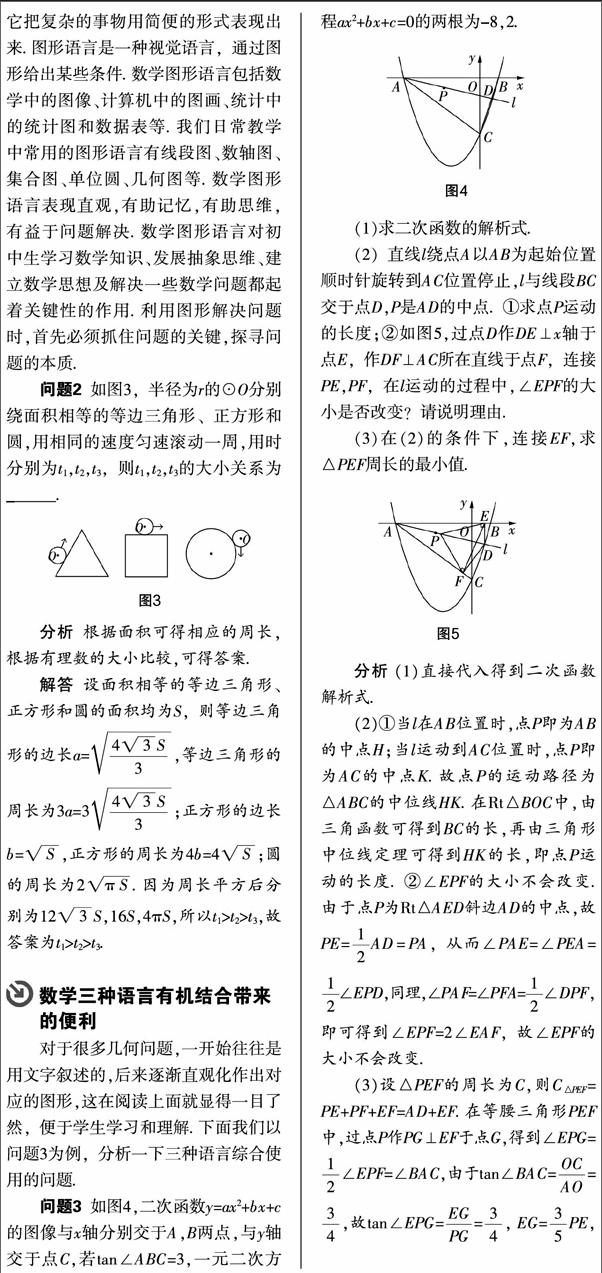
问题3 如图4，二次函数y=ax2+bx+c的图像与x轴分别交于A，B两点，与y轴交于点C，若tan∠ABC=3，一元二次方程ax2+bx+c=0的两根为-8，2.

（1）求二次函数的解析式.

（2）直线l绕点A以AB为起始位置顺时针旋转到AC位置停止，l与线段BC交于点D，P是AD的中点.①求点P运动的长度；②如图5，过点D作DE⊥x轴于点E，作DF⊥AC所在直线于点F，连接PE，PF，在l运动的过程中，∠EPF的大小是否改变？请说明理由.

（3）在（2）的条件下，连接EF，求△PEF周长的最小值.

分析 （1）直接代入得到二次函数解析式.

（2）①当l在AB位置时，点P即为AB的中点H；当l运动到AC位置时，点P即为AC的中点K. 故点P的运动路径为△ABC的中位线HK. 在Rt△BOC中，由三角函数可得到BC的长，再由三角形中位线定理可得到HK的长，即点P运动的长度.②∠EPF的大小不会改变. 由于点P为Rt△AED斜边AD的中点，故PE=AD=PA，从而∠PAE=∠PEA=∠EPD，同理，∠PAF=∠PFA=∠DPF，即可得到∠EPF=2∠EAF，故∠EPF的大小不会改变.

（3）设△PEF的周长为C，则C△PEF=PE+PF+EF=AD+EF. 在等腰三角形PEF中，过点P作PG⊥EF于点G，得到∠EPG=∠EPF=∠BAC，由于tan∠BAC==，故tan∠EPG==， EG=PE，EF=PE=AD. 从而有C△PEF=AD+EF=1+AD=AD. 又当AD⊥BC时，AD最小，此时C△PEF最小. 于是可得到C△PEF的最小值.

通过上述问题的描述，我们可以看到数学语言转化能力的重要性和切需性. 为了提高语言转化能力，在图形的基础上，我们不妨多使用几何语言进行常规描述，帮助学生提高对问题的理解和消化. 教师在教学中，只有认识到语言教学和理解的重要性，才能在平时多关注学生这些方面能力的提升，也才能帮助学生提高数学理解的同时，加强对数学知识和数学思维能力方面的综合训练. 总之，阅读应当立足于学生的数学现实，站在学生的角度寻找学生的学习起点和老师教学起点的对接点.