我国农业生产的技术效率及其影响因素

白玛雍珍

内容摘要：本文依据我国31个省区市2008-2014年农业的投入产出数据，建立基于超越对数生产函数的SFA模型，对各省区市的农业生产技术效率进行了测算，研究发现我国农业技术效率整体呈上升趋势，但平均技术效率水平较低，与生产前沿面存在较大距离。我国农业技术效率的区域差异明显，政府应鼓励东部地区和东北地区提高农业的机械化水平，同时创新对中西部的农业投入方式，加强农业基础设施建设。土地和资本对农业产出的贡献最大，而农业劳动力则相对过剩，应通过向非农产业转移和农业内部提升来吸纳农村剩余劳动力。在影响技术效率的因素中，有效灌溉率和人均农机总动力对农业技术效率的促进作用最大，各省区市应注重改善农村水利设施条件并推动农业的规模化与机械化生产。

关键词：农业生产效率 超越对数生产函数 随机前沿分析（SFA）

引言

2015年我国农林牧渔业增加值为60863亿元，占全国GDP总量的9%。农业经济的增长一方面依赖于投入要素的增加，另一方面取决于农业生产效率的提高。随着我国城镇化建设的推进，大量农村人口涌入城市，农业人口大幅度减少，同时由于环境恶化导致实际可播种面积减少，因此未来农业产出的增加越来越依靠农业生产技术效率的提高。目前，理论界对效率问题的研究主要采用非参数法和参数法两类方法，非参数法以数据包络分析（DEA）为代表，而参数法则以随机前沿分析（SFA）为代表。迄今为止，国内外学者围绕农业生产的技术效率已经展开了许多有益的研究。Farrell（1957）在衡量英国农业生产效率时，最早提出了生产前沿的方法，随后引起了各国学者采用生产前沿研究不同行业生产效率的热潮。Ruttan（2002）对世界不同国家的农业生产效率进行了研究，发现发达国家和发展中国家的农业增长路径存在明显差异。K Galanopoulos等（2004） 测算了欧盟国家和13个候选国家1993-1999年的农业技术效率，发现欧盟国家的农业技术效率在这七年间先有上升，然后略有下降。国内学者田翠杰（2011）、黎哲延（2014）、秦菲等（2014）、钟苏侨（2015）采用DEA方法分别对天津、海南、江西、福建等省市的农业生产效率进行了研究，研究一致认为各省区市的农业技术效率均有所改进，但内部地区的农业生产效率差异显著。由于随机前沿分析（SFA）具有分离技术无效项与随机误差项等优势，越来越多的学者开始使用该方法评价技术效率。鲍学东（2009）在研究四川省的农业技术效率时，建立了随机前沿的生产函数模型，发现四川的农业经济增长主要依赖土地和资本的投入。岳慧丽等（2014）采用随机前沿分析方法分析了河北省140个区县的农业技术效率，发现河北省农业技术效率整体呈上升趋势，但农业技术效率普遍较低。DEA方法在分析技术效率时假定所有的样本共用一个固定的生产前沿面，而实际上样本存在异质性，每个样本的前沿面应该是随机的。同时，农业生产受到诸多因素的影响，存在较大的噪声，而DEA方法容易忽略噪声对生产活动的真实影响，从而导致估计结果有偏差。DEA方法在我国农业生产效率的探索中已经得到了广泛的应用，而SFA方法的应用则相对比较有限。因此，本文在对我国31个省区市2008-2014年的农业生产技术效率变动进行测算时，拟采用随机前沿分析（SFA）方法，分析其效率的变动趋势、区域差异及影响技术效率的因素，为推动我国农业经济又好又快发展提供参考依据。

农业技术效率测度模型构建和数据来源

（一）模型构建

农业生产与其它行业存在较大差异，存在许多不可控制的因素，极易受到自然资源、气候条件、测量误差等诸多统计噪声的影响，从而出现一些奇异值。

随机前沿模型中的随机干扰项可以与农业生产特征保持一致，正是由于随机前沿模型的优越性，将其应用到农业效率测量中具有一定的优势。Battese、Coelli（1993）考虑到传统的随机前沿模型无法反映横截面数据或个体样本间的差异情况，又进一步改进了传统的随机前沿模型，通过“一步法”便可同时对技术效率和技术无效项进行估计。在生产函数的选择方面，由于超越对数生产函数可以作为任意生产函数的二阶泰勒近似，形式较为灵活，不仅考虑了技术进步，而且考虑了投入要素对生产效率的协同效应。因此，本文选择超越对数生产函数作为随机前沿函数的一般形式，其具体模型如下：

其中，i表示我国的第i个省区市，i=1，2，…，31；t表示时期，t=1，2，…，7；产出变量Yit是我国第i个省区市第t年的农林牧渔业总产值（以2001年不变价格计算）。投入变量主要有四个，包括农林牧渔业从业人员数、农作物总播种面积、农业机械总动力和化肥施用量（折纯量），Lit表示第i个省区市第t年的农林牧渔业从业人员数，代表农业的劳动力投入；Ait表示第i个省区市第t年的农作物总播种面积，代表农业的土地投入，播种面积比耕地面积更能代表农业土地的实际利用情况，因为随着农民的进城，农业弃耕、休耕的现象比较普遍；Eit表示第i个省区市第t年的农业机械总动力，包括大中小型拖拉机、农用柴油机、农用电动机、农用水泵、联合收割机等各类农用机械的动力总和，Fit是第i个省区市第t年的化肥施用量（折纯量），这两项共同代表农业的资本投入。β0为截距项，β1、β2、β3、β4为待估参数，β5、β6、…、β10为投入要素之间的交叉项系数，β11、β12、β13、β14为投入要素的二次项系数，vit是随机误差项，uit是非负技术无效项，分别服从N（0，σ2v）和N（0，σ2u）的正态分布。其中交叉项和二次项系数满足下列限制条件：

同时，影响农业生产技术效率的因素还有很多，如农业技术创新、农业经营或组织形式、劳动者素质等。限于数据的可得性，本文主要考察以下几个因素： 一是地区人均GDP（PGDP），反映各个地区的经济发展水平；二是复种指数（CI），即农作物总播种面积与耕地面积之比，复种指数受当地土壤、水分、肥料和科学技术水平等因素的综合影响，可以反映当地的农业自然生产条件；三是有效灌溉率（IR），即有效灌溉面积与耕地面积之比，用以反映农业生产的水利条件；四是人均耕地面积（PA），即耕地面积除以农林牧渔从业人员数；五是人均农机总动力（PE），即农机总动力除以农林牧渔从业人员数；六是人均化肥施用量（PF），即化肥施用量除以农林牧渔从业人员数。将各变量均取自然对数，其技术效率损失的函数可以设定为：

uit=α0+α1lnPGDPit+α2lnCIit+α3lnIRit+α4lnPAit+α5lnPEit+α6lnPFit

（二）数据来源

本研究所需的数据是2008-2014年我国31个省区市农业投入产出的面板数据，相关基础数据主要来源于2009-2015年《中国统计年鉴》和《中国农村统计年鉴》。由于劳动力是时点数据，本文在计算农业劳动力人数时，以每年年初（或上年年底）的农林牧渔从业人员数和年底从业人员数的平均值作为当年的实际劳动投入量。为排除通货膨胀等因素的影响，农林牧渔业总产值和人均GDP均采用2001年不变价格计算。

模型估计结果和技术效率分析

（一）我国农业生产的技术效率分析

根据收集整理的数据，运行Frontier4.1软件，可以得到2008-2014年我国31个省区市的农业技术效率值，从数据结果来看，7年来我国农业的平均技术效率水平为61.29%，与生产前沿面仍存在一定的距离，说明投入要素的使用效率还有待改进，但农业的平均技术效率水平总体呈上升趋势。

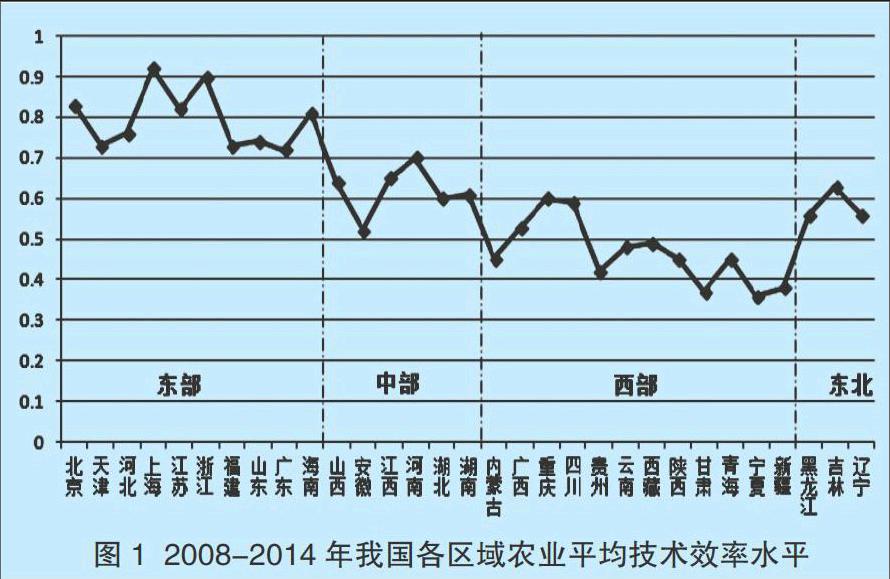
我国农业技术效率的地区差距明显，为了更清楚地显示我国农业生产技术效率的区域差异，现按照我国最新的区域划分方法，将我国划分为东部、中部、西部和东北地区四个区域，将我国各区域7年来的平均技术效率水平进行对比，结果如图1所示。

从我国各区域的平均技术效率水平来看，最高的是东部地区，其次是中部地区，之后是东北地区，最低的是西部地区。其中，东部地区省区市的平均效率水平为79.6%，中部地区为62.0%，东北地区为58.3%，西部地区为46.4%，总体上呈现出东高西低的特征，且东部地区的平均效率水平比西部地区高33.2个百分点。而匡远凤（2012）通过对我国农业劳动生产率进行四重分解，研究发现我国东部、中部、西部和东北地区的农业技术效率差距仍有不断拉大的趋势。因此，政府必须高度重视我国农业技术效率差距的扩散现象。

（二）随机前沿生产函数估计结果与分析

将Frontier4.1的运行数据结果进行整理，其随机前沿生产函数的参数估计结果如表1所示。

γ值可用于检验模型的有效性，若接近于零，则表明技术无效项为一常数，模型采用OLS估计即可，表1中γ值显著大于零且通过了1%的显著性检验，证明采用随机前沿模型是合适的。γ还可以表示随机扰动项中技术无效项所占的比例，而本文估计的γ值为0.8653，说明误差项中有86.53%来自于技术的效率损失，误差主要来源于技术非效率，而剩余的13.47%来自于统计随机误差。单边似然比在1%水平下显著，说明误差项具有明显的复合结构，表明我国农业技术效率的确存在效率损失。

从参数的t检验来看，大多数变量均通过了显著性检验，证明变量的选取是合适的。β1、β2、β3、β4的系数均为正，表明随着投入的增加，产出也会得到不同程度的增加，按照系数的大小可以看出对产出起主导作用的是土地和资本要素的投入。从交叉项系数来看，β5=-0.4123表示当农业机械总动力和化肥施用量（折纯量）保持不变时，劳动力和农业总播种面积同时增加一个单位，产出将减少0.4123个单位；同理，β6=-0.2345表示当农业总播种面积和化肥施用量（折纯量）保持不变时，劳动力和农业机械总动力同时增加一个单位，产出将减少0.2345个单位；而β7=-0.7568表示当农业总播种面积和农业机械总动力保持不变时，劳动力和化肥施用量（折纯量）同时增加一个单位，产出将减少0.7568个单位。上述交叉项系数共同表明在追加投入要素时，劳动力投入存在过剩现象，导致劳动与其它投入要素的交叉项系数均为负，生产要素存在一定程度的误配。

（三）技术效率的影响因素分析

随机前沿分析可以通过“一步法”来分析技术效率和技术无效项，其技术无效项的系数如表2所示。

从表2可以看出，人均耕地面积变量的系数不显著，说明人均耕地面积的变化对农业生产效率的影响不大，人均耕地面积的增加、生产规模的扩大并不能很好地促进我国农业生产效率的提高。但其它五个变量均通过了显著性检验，其中有效灌溉率、人均农机总动力和人均GDP的系数为负，说明这些因素有利于提高农业生产技术效率。有效灌溉率（IR）对农业技术效率的促进作用最大，表明农业生产依赖于良好的水利条件，而在对中西部地区的农业生产效率进行单独分析时，发现有效灌溉率对农业技术效率的提升作用高于平均水平，这可能和中西部的农业自然条件有一定的关系。人均农机总动力（PE）的系数为-0.5213，表明人均农机总动力的增加通过提高农业的机械化和规模化生产水平，进而改进了农业的生产效率。人均GDP的系数为-0.2402，这表明区域经济发展和城镇化水平提高对农业具有较强的带动作用，党的“十八大”提出要“四化同步”，坚持新型工业化、信息化、城镇化和农业现代化的同步发展。人均化肥施用量的系数为0.1053，与农业技术效率负相关，说明我国在农业生产中存在过度使用化肥的现象，化肥容易污染土地，造成土地退化，影响了农业的生态环境，降低了农业的生产效率。复种指数的系数为0.0123，表明复种指数的增加不利于农业生产技术效率的提高。复种指数越高，表明对同一块耕地的耕种次数越多，会有利于增加农业产出。但同时农民也有可能过于依赖优越的自然环境而放弃更新使用高效率的设备，从长远来看，会对技术在农业中的应用起到抑制作用，从而降低农业的技术效率。

结论和政策建议

本文采用基于超越对数生产函数的随机前沿分析方法对2008-2014年我国31个省区市的农业生产技术效率进行了测度，并在将我国划分为东部、中部、西部和东北四个区域的基础上，分析了四大区域之间的效率差异及影响效率的主要因素，可以得出以下结论，并针对性地提出建议：

第一，我国农业的平均技术效率水平总体呈上升趋势，但平均技术效率水平仅为61.29%，与生产前沿面有较大距离，存在较大的改进空间。我国31个省区市四大区域的农业技术效率水平差异明显，总体呈现出东高西低的特征。我国东部地区大多沿海，经济发达，农业生产条件较为优越，中西部地区相对较为干燥，且存在较多沙漠地区，而匡远凤（2012）认为这种差距在未来仍有不断扩大的趋势。农业是一国的根本，政府应鼓励东部地区和东北地区提高农业的机械化水平，改进农业生产效率。同时，政府要高度重视中西部农业效率低下的现状，深入思考其深层次原因，创新对中西部的农业投入方式，加强农业基础设施建设，实现农业的适度规模经营。

第二，研究表明我国农业产出主要依赖于土地和资本要素的投入，而农业劳动力投入处于相对过剩状态，超过了农业生产最佳的劳动力需求（唐建军等，2010），未来应考虑通过多种途径有效转移农村剩余劳动力。一方面，随着我国城镇化进程的加快，可以通过城镇化的发展转移一部分农业剩余劳动力。但是，城镇化也带来了留守儿童和空巢老人的社会问题。因此，另一部分剩余劳动力可以考虑在农村当地解决。政府可以通过扶持发展一批农业龙头企业，通过龙头企业带动相关企业对农产品进行深加工，延伸农业产业链来拓宽农村劳动力的就业渠道，从而优化农业的产业结构，提高农民的收入水平。

第三，有效灌溉率和人均农机总动力均对农业技术效率具有较大的促进作用，各省区市应注重改善农村的水利设施条件并推动农业的规模化机械化生产，政府在未来应坚持农机具购买的补贴政策，并在有条件的地区加大补贴力度。人均耕地面积对效率的改进作用不明显，说明农业土地的规模经济不明显，政府应加速土地流转，鼓励农民将土地承包给专业大户和合作社，为规模化经营和机械化操作创造更多有利的条件，从而大幅度提升农业生产效率。

参考文献：

1.Farrell M.J.The Measurement of Productive Efficiency [J].Journal of the Royal Statistical Society，1957

2.Ruttan V.W.Productivity Growth in World Agriculture，Sources and Constraints [J].Journal of Economic Perspectives，2002（4）

3.K Galanopoulos，G Karagiannis，Koutroumanidis.Malmquist productivity index estimates for European agriculture in the 1990s[J].Operational Research，2004（1）

4.田翠杰.基于DEA方法的天津农业技术效率分析[J].经济研究导刊，2011（23）

5.黎哲延.基于DEA的海南省农业生产效率评价研究[J].农村经济与科技，2014（8）

6.秦菲，舒晓波，肖素芳，胡丹.基于DEA的江西省农业生产效率时空特征研究[J].江西科学，2014（5）

7.钟苏侨.基于DEA模型的福建省农业生产效率评价[J].福建商业高等专科学校学报，2015（4）

8.鲍学东.基于SFA的四川农业生产技术效率研究[D].四川农业大学，2009

9.岳慧丽，诸叶平，雪燕，许金普.基于随机前沿分析方法的河北县域农业技术效率及影响因素研究[J].江苏农业科学，2014（9）

10.匡远凤.技术效率、技术进步、要素积累与中国农业经济增长—基于SFA的经验分析[J].数量经济技术经济研究，2012（1）

11.Battese G E，Coelli T J.A stochastic frontier production function incorporating a model for technical inefficiency effects[M].Armidale：Department of Econometrics，University of New England，1993

12.唐建军，王礼力.基于DEA模型的陕西各地区农业技术效率分析[J].陕西农业科学，2010（4）