基于灰色时间序列组合的隧道变形预测研究
黄永红
(重庆市勘测院,重庆 400020)
基于灰色时间序列组合的隧道变形预测研究
黄永红*
(重庆市勘测院,重庆 400020)
随着各大城市地铁的兴建,各种工程事故相继发生,隧道开挖具有复杂性和特殊性,充分认识和掌握隧道围岩的变形规律,对于避免不必要的工程事故具有重要意义。本文基于隧道围岩施工期的变形监测数据,深入研究了时间序列分析、灰色系统理论和组合模型预测方法。结果表明,MGM(1,3)+AR(3)组合模型不仅能够反映数据序列的发展变化的趋势性,而且还能考虑数据序列随机波动的影响,组合模型拟合与预测的模拟预测精度高。研究成果为隧道围岩施工期和运行期的安全提供可靠依据,并未科学研究和理论计算提供参考。
灰色;时间序列;围岩;变形预测
1 引 言
随着城市地铁隧道工程的蓬勃发展,出现了因地下工程施工而引起的各种事故[1-3]。例如:地下工程施工会引起地层移动而导致不同程度的沉降和位移,当地层移动和地表变形超过一定的限度时就会造成地面沉陷、基坑垮塌、隧道破坏、周边建筑物损害、地下管线损害等事故,导致严重经济损失并产生不良的社会影响,从而影响到隧道和地表建筑物的正常使用和安全运营[4]。尤其对于城市地铁,一般都穿越城市中心地带,因建筑物密集、施工场地狭小、地质情况复杂、地下管网密布、交通繁忙、施工条件受到限制,对环境的控制要求更为严格。为了保证隧道工程的进行以及周围(建)构筑物的安全,密切监测围岩变形,提出较为可靠的围岩变形预测方法就显得十分必要和重要。
时间序列分析是基于动态数据解释系统动态结构和规律的统计方法,是数理统计学中的重要分支之一[5,6]。其基本原理是基于系统有限次数的观察数据,建立能够比较精确地反映时间序列中所包含的动态依存关系的数学模型,借助模型对系统未来的行为进行预报,因而可以作为因果关系统计模型的补充。然而时间序列分析方法适用于平稳时间序列建模,但实际围岩变形监测数据既非平稳的又非等间距的,因此如何对监测资料进行等间距和平稳化处理,使其适合建立平稳时间序列模型,是需要研究的一个问题。灰色系统模型是处理数据量少、信息贫乏、不确定性问题的有效方法。均值GM(1,1)模型参数在模型建立后一直保持不变,而围岩变形随着时间而变化,其对应的模型的参数必然发生变化,因此均值GM(1,1)模型的适用性受到限制[7,8]。鉴于以上原因,将灰色与时间序列组合,实现优势互补,从而全面系统的反映效应量的信息是本文要做的主要工作。
2 时间序列的建模
时间序列分析建模预报的过程是:首先判断模型类型与模型阶数,即数据序列适合建立AR(p)模型、MA(q)模型还是ARMA(p,q)模型,并定出合适的模型阶数p和q;其次估计计算相应模型的参数值φ=(φ1,φ2,…,φp)T及θ=(θ1,θ2,…,θq)T;再次检验残差εt是否为平稳白噪声;最后利用通过检验的模型进行预报[9]。
理论上任何ARMA(p,q)模型均可以转化为 AR(p)模型,从方便实用的角度出发,本文全部采用 AR(p)模型。
2.1 AR(p)模型的χ2检验
模型检验就是对残差序列{ε(t),t∈Z}进行检验。如果建立的模型已经完全将原时间序列包含的所有变化趋势提取出来,则{ε(t),t∈Z}是平稳白噪声序列,从而证明建立的模型是合适的;反之,若残差序列不是平稳白噪声序列,则表明建立的模型没能将原数据序列的变化趋势提取完全,因而应进一步对模型进行修正或重新建立模型[10]。
对于AR(p)模型,残差为:

构造χ2的检验统计量:
检验的假设:
H0:ρK=0,当k≥m;H0:ρK≠0,对某些当k≤m。
2.2 AR(p)模型的预报
AR(p)的最小均方误差预测公式为
(1)
则根据式(1),AR(p)的递推预测公式可表示为
AR(p)模型的最小均方预测公式简便实用,根据xm,xm-1,…,xm-p+1即可求得多步的预测值,因而其适用性较强。
3 灰色系统GM(1,1)建模
3.1 数据序列预处理
原始数据序列为:
X(0)=[x(0)(1),x(0)(2),…x(0)(n)]
将X(1)(k)做一次累加:
X(1)=[x(1)(1),x1(2),…x(1)(n)]
计算X(1)(k)背景值:
3.2 建立一阶微分方程
3.3 微分方程的解
用最小二乘法求解参数a和b,得:
A=[a,b]T=(BTB)-1BTYn

模拟预测值表达式为:

(1)残差检验
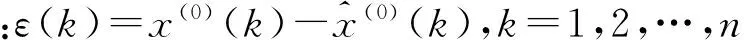

(2)均方差比值检验与小误差概率检验
X(0)(k)的均值和方差:
ε(k)的均值和方差:
计算均方差比值C及小概率误差P:
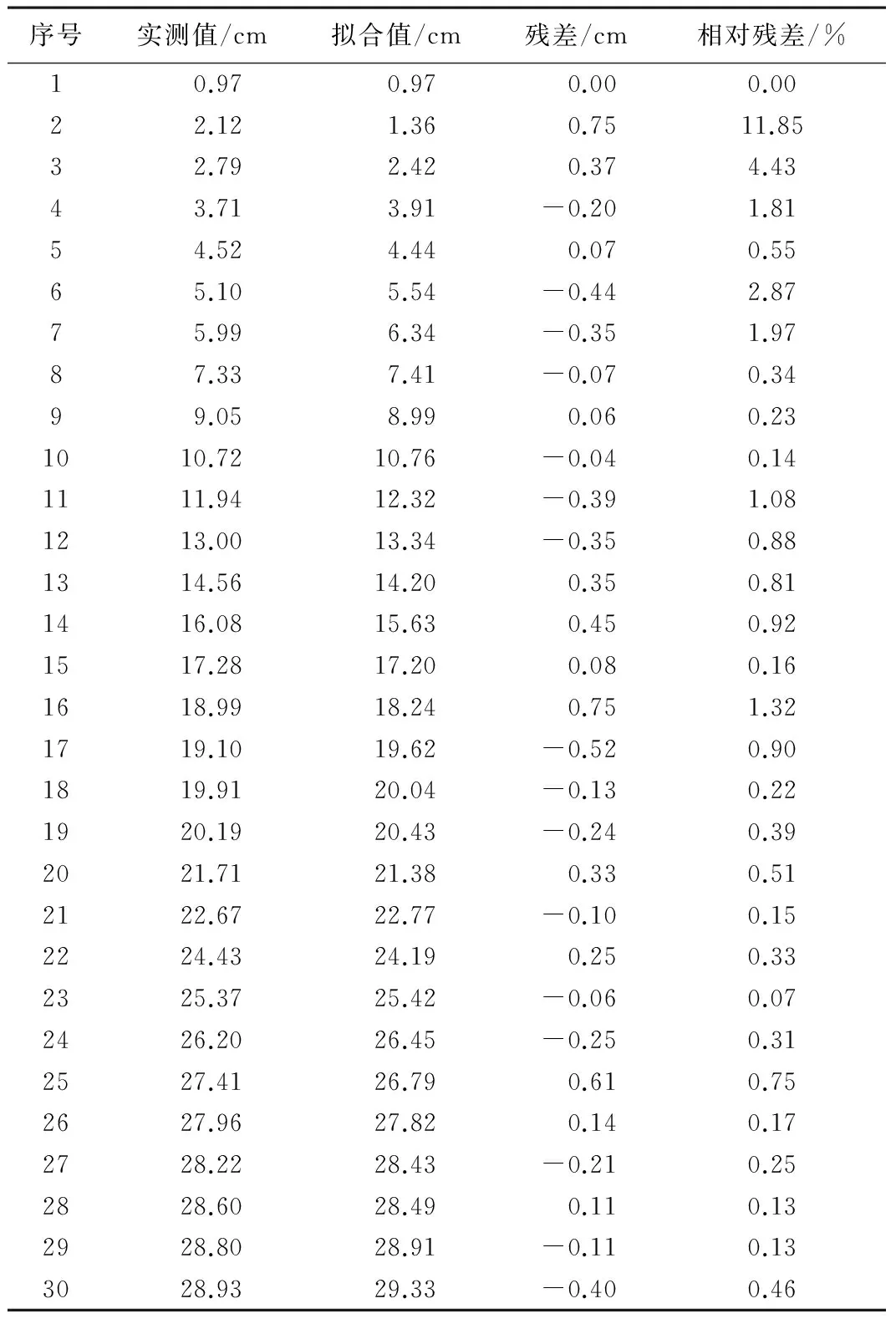
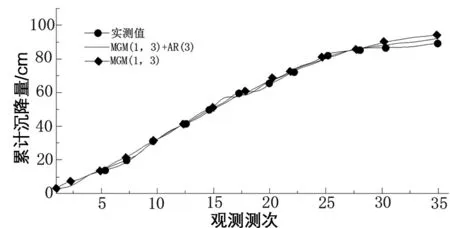
均方差比值合格模型要求:对于给定的C0>0,C 小误差概率合格模型要求:对于给定的P0>0,P 4.1 组合预测的权重组合模型 单个模型能针对效应量的某些影响因素构建模型进行预测,反映这些因素对效应量的影响,因而具有一定的局限性。而实际上,效应量与其影响因素之间的关系是复杂多变的,单项模型难以反映全部环境量对效应量变性规律的影响[11]。 组合预测理论认为:对同一个研究对象,组合预测方法将建立在不同信息基础上的单项模型有机的组合在一起,综合各个模型的优点实现优势互补,从而全面系统综合地反映物体的变形情况,提高预测精度。组合模型并不是各个模型的简单拼盘,每个单项模型都不是孤立存在的,而是彼此联系的,共同组成一个复杂的政体。组合预测模型大多优于单项模型的预测效果[12]。 权重组合模型: 其中:wj表示第j个模型在组合模型中的权重,wj应满足 权重系数wj可以通过多种计算方法就求解得到,常用的有均方导数法、方差倒数法、算术平均法、最优加权法、标准差法、简单加权法等。本章介绍最优加权法。4.2 组合模型最优权系数 将误差统计量选定为拟合误差et,则线性规划模型可表示为: (2) 用矩阵表示上式中的各项,即: W=(w1,w2,…,wJ)T,R=(1,1,…,1)T ej=[e1(j),e2(j),…,eN(j)]T e=[e1,e2,…,eN]T,j=1,2,…,J E为正定对称矩阵,则: 式(2)可表示为: 引进Lagrange乘子,求极小值: 即:EW-λR=0,W=λE-1R 可得:RTW=1,即RT(λE-1R)=1 因而Lagrange乘子λ可表示为: λ=(RTE-1R)-1 最优权W0和最小值Q0为: (RTE-1R)-1E-1R=W0 (RTE-1R)-1=Q0 4.3 算例分析 某地铁隧道是某地铁一号线一个重要标段,而三线大跨隧道施工是本标段控制工期的关键,L=127.225 m,主要穿越K1g-2-3a泥质粉砂岩(中~微风化),洞口地段穿越粉质黏土、粉质黏土混卵砾石、强风化泥质粉砂岩,拱顶覆土厚度 0.5 m~30 m。 施工中建立了位移监测系统,它主要根据位移时间曲线来描述围岩的变形,以便了解围岩松动破坏范围,对围岩稳定性作评价。 选择RK1+062断面位移监测数据作建模分析,具有典型意义。数据单位为mm。 V7测点实测值与MGM(1,3)+AR(3)模型拟合值对比表 表1 V7测点MGM(1,3)模型与MGM(1,3)+AR(3) 图1 实测曲线与MGM(1,3)、MGM(1,3)+AR(3)与拟合预测曲线 本文讨论了组合预测模型理论,并基于桩基沉降变形数据建立相应的组合模型,组合模型综合了单项模型的优点,提高了模拟预测精度。 MGM(1,3)和AR(3)的权重组合模型综合了灰色模型和时间序列模型的优点,既反映数据序列变化的趋势项又考虑数据序列随机波动的影响,这是单项模型所不具备的;组合模型拟合与预测精度均比单个模型高;组合模型的短期预报精度高,中长期预报精度低;组合模型的模拟预测精度受到单项模型的限制,单项模型的精度较低时,组合模型的精度也较低。 MGM(1,3)+AR(3)组合模型不仅能够反映数据序列的发展变化的趋势性,而且还能考虑数据序列随机波动的影响,与MGM(1,3)模型相比,组合模型拟合与预测的模拟预测精度高。 [1] 刘军,易胜文,晋涛等. 改进的灰色模型在建筑物沉降预测中的应用研究[J]. 城市勘测,2015,144(1):149~151.[2] 潘华志,卫建东,夏治国等. 实时灰色模型在变形预测中的应用[J]. 测绘科学,2007.07,32(4). [3] 刘棠洪,周俊,朱庆川. 改进的灰色预测模型在地面沉降预测中的应用[J]. 地质灾害与环境保护,2007.09,18(3).[4] Wang Z,Woodward W A,Gray H L. The application of the Kalman filter to nonstationary time series through time deformation[J]. Journal of Time Series Analysis,2009,30(5):559~574. [5] Dong-Jian Z,Chong-Shi G.,et al. Time series evolution forecasting model of slope deformation based on multiple factors[J]. Chinese Journal of Rock Mechanics and Engineering,2005,24(17):3180~3184. [6] 张非非,胡健,佘兆宇. 基于优化的GM(1,1)模型在高速公路沉降预报中的应用[J]. 城市勘测,2014,139(2):154~156. [7] Fernández J,Tizzani P,Manzo M,et al. Gravity‐driven deformation of Tenerife measured by InSAR time series analysis[J]. Geophysical Research Letters,2009,36(4). [8] Henderson S T,Pritchard M E. Decadal volcanic deformation in the Central Andes Volcanic Zone revealed by InSAR time series[J]. Geochemistry,Geophysics,Geosystems,2013,14(5):1358~1374. [9] 陈玲菊. 改进GM(1,1)在高铁隧道沉降变形预测中的对比应用[J]. 城市勘测,2015,144(1):142~145. [10] Samsonov S,d’Oreye N,Smets B. Ground deformation associated with post-mining activity at the French-German border revealed by novel InSAR time series method[J]. International journal of applied earth observation and geoinformation. 2013,23:142~54. [11] 夏力. 改进的灰色模型在高铁沉降预测中的应用研究[J]. 城市勘测,2015,147(4):148~151. [12] Hetland EA,Musé P,Simons M,et al. Multiscale InSAR time series (MInTS) analysis of surface deformation[J]. Journal of Geophysical Research:Solid Earth. 2012,117(B2). Deformation Prediction of Tunnel Surrounding Rock Based on Grey Time Series Combined Model Huang Yonghong (Chongqing Survey Institute,Chongqing 400020,China) With more and more subway construction in big cities,engineering accidents occurred one after another. For the tunnel excavation has the complexity and the particularity,it is very important to fully understand and grasp the deformation rule of tunnel surrounding rock,so as to avoid unnecessary accidents. Based on the deformation monitoring data of tunnel surrounding rock during construction,in this paper the time series analysis,the grey system theory and the combination model prediction method are studied. The results show that the MGM(1,3)+AR(3) model combination can not only reflect the trend of the development and change of the sequence data,but also consider the effects of stochastic fluctuations in the data sequence,which can fit and forecast with high precision. The research results provide a reliable basis for the safety of the tunnel surrounding rock construction period and operation period,and provide reference for scientific research and theoretical calculation. grey;time series;surrounding rock;deformation prediction 1672-8262(2016)06-127-04 TU413.6 A 2016—05—03 黄永红(1966—),男,高级工程师,主要从事测绘监测工作。 国家自然科学基金项目(51408191)4 灰色时间序列组合模型的工程应用
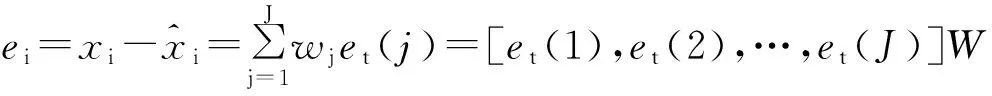
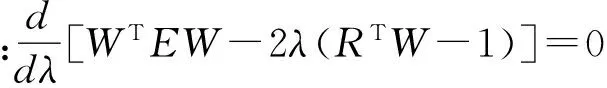

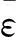
5 结 论

