基于时域平滑约束的脑磁时序信号逆问题求解方法

刘 婷,戴亚康,杨莹雪,王玉平

(1.中国科学院苏州生物医学工程技术研究所,江苏苏州 215163;2.中国科学院长春光学精密机械与物理研究所,吉林长春 130033;3.中国科学院大学,北京 100049;4.首都医科大学宣武医院神经内科,北京 100053;5.脑功能疾病调控治疗北京市重点实验室,北京 100053 )

基于时域平滑约束的脑磁时序信号逆问题求解方法

刘 婷1,2,3,戴亚康1,杨莹雪4,5,王玉平4,5

(1.中国科学院苏州生物医学工程技术研究所,江苏苏州 215163;2.中国科学院长春光学精密机械与物理研究所,吉林长春 130033;3.中国科学院大学,北京 100049;4.首都医科大学宣武医院神经内科,北京 100053;5.脑功能疾病调控治疗北京市重点实验室,北京 100053 )

由脑磁时序信号重建脑内时序神经信号时,除了要保证重建信号位置和强度的准确性,还要避免重建源信号在时域上瞬变.针对这一问题,提出了一种基于时域平滑约束的脑磁时序信号逆问题求解方法.该方法不同于传统最小范数估计算法(Minimum Norm Estimate,MNE),通过引入时域平滑正则算子构造双参数混合正则化,根据广义交叉验证(Generalized Cross-Validation,GCV)原则选取双正则化参数后,根据单正则项的解在源信号中的权重将其进行线性组合估算出源信号.仿真数据实验表明,本文方法比传统MNE方法的总体均方误差小,且各时刻均方误差基本稳定在同一水平;同时本文方法重建的源信号与仿真源信号变化趋势基本一致.真实数据实验发现,本文方法重建结果的曲率变化率为0.0640,而传统MNE方法重建结果的曲率变化率为0.1646.实验结果证明本文方法能重建出空域准确且时域平滑的脑内神经信号.

脑磁时序信号;逆问题;双参数混合正则化;时域平滑

1 引言

人类的脑部活动与大脑细胞活动息息相关,其中最主要的脑细胞——神经元——是大脑神经传递的主体,它通过产生动作电位来传递神经信号.脑物理学认为,如果把人类大脑看作是电磁系统时,它遵守物理学中的电磁规律,由受到刺激或心理活动激活的神经元充当激励脑电磁场的源[1].脑磁图(MagnetoEncephaloGraphy,MEG)是测量脑神经信号的非侵入性脑功能检测技术,它利用超导线圈在脑外测量神经元产生的微弱磁场,通过分析MEG信号反推大脑内部神经元活动,此即脑磁逆问题.脑磁逆问题有两个难点:一是解的非唯一性,二是解的不稳定性.为了能够得到稳定、合理的解,必须通过先验知识在逆问题求解过程中对解空间加以约束,即引入正则化技术[2,3].从上个世纪90年代开始科学家们提出了诸多脑内源定位技术,其中开展最早且被普遍采用的方法是最小范数估计算法[4](Minimum Norm Estimate,MNE).此算法的本质是寻找最小能量解,通过采用Tikhonov正则化[3]平衡数学模型误差与源能量,以全局能量最小的源来推算脑内源信号的位置和强度.

近年来随着研究的进展,人们开始探索诸如注意机制、冲突处理等的神经传导机制.科学家们不再满足于只获知单一时刻脑内源信号的位置、强度,还希望获知脑内神经信号的定向传导过程,也就是脑磁源时序信号.脑神经学认为,相邻脑结构之间的兴奋传导间隔几个到几十个毫秒之间[5],而不会有相邻时刻间跳变的现象.由于没有施加时域约束,传统MNE方法重建出来的脑磁源信号往往偏离原始时序源信号的变化趋势,在时域上有明显的跳变现象,这与神经信号的定向传导机制相违背[6].为此,本文提出基于时域平滑约束的MEG时序信号逆问题求解方法.该方法从传统MNE方法出发,在Tikhonov正则化中引入时域平滑约束项,构造双参数混合正则化,根据广义交叉验证(Generalized Cross-Validation,GCV)准则选取两个合适正则化参数后,通过计算单正则项的解在源信号中占的权重然后进行线性组合估算出源信号.仿真实验表明,本文提出的方法不仅可以准确重建脑磁源,而且重建的时序源信号能更好地还原真实源信号的变化趋势,大大改善传统MNE方法重建结果在时域上振荡的现象.该方法将在正文第二部分详细描述,第三部分是仿真、真实数据实验和实验结果,最后是本文的讨论部分.

2 理论和方法

假设脑外有m个通道的MEG信号,脑内有n个均匀分布的源信号,那么在i时刻脑内源信号与MEG信号的关系可以用以下离散化线性模型[7]表示:

bi=Axi+ei

(1)

其中bi为i时刻大小为m×1的MEG测量信号;xi为i时刻脑内源信号,大小为n×1;ei是i时刻和bi同维度的噪声信号;A为转换矩阵,代表脑内源信号与MEG测量信号的映射关系,大小为m×n.矩阵A可以通过边界元方法、有限元方法等结合头模型求解.脑磁逆问题的求解面临两个难点:一是解的非唯一性,由于MEG信号通道数m远小于脑皮层网格数n,所以式(1)是高度欠定方程,有无数个解;二是解的不稳定性,即病态性,由于矩阵A的条件数,即最大特征值与最小特征值之比很大,MEG测量信号中很小的噪声都将对解产生很大的扰动.基于以上问题,对式(1)求解xi转化为求解最小二次泛函的问题,并且引入Tikhonov正则化技术来使病态问题适定化.具体地,在第i时刻,脑磁逆问题求解转化为求解以下最小值问题:

(2)

等式右边第一项表示测量数据和估计数据的拟合,第二项为正则项,表示解的先验信息,其中R为约束解空间的正则算子,λ为正则化参数,调节拟合项和正则项在两项之间达到平衡.当R为单位阵时,式(2)为Tikhonov零阶正则化,约束项使解具有全局最小能量;当R为一阶或者二阶微分矩阵时,式(2)为广义Tikhonov正则化,约束项使解具有光滑的曲面梯度或曲率.由于矩阵A为行满秩,计算其Moore-Penrose右逆矩阵,式(2)对应的解的形式为:

(3)

如前所述,式(2)所示目标函数重建出来的源信号各个时刻之间是相独立的(可以通过第二部分仿真实验的结果看到).为保证时域平滑性,我们对式(2)增加时域平滑约束项,以构造双参数混合正则化来重建MEG时序源信号,下面介绍具体方法.

2.1 目标函数构造

首先将式(1)转化成时序信号形式.对于时长为k的MEG测量信号,对应的离散化线性模型为:

b=Ax+e

(4)

其中b为MEG测量信号,大小为m×k;A是m×n维转换矩阵,x为n×k维时序源信号矩阵;e为m×k维噪声信号矩阵.

根据MNE算法的思想,新的目标函数既要满足重建的源信号在整个k时段所有解中能量最小,又要满足在相邻时刻间是平滑的[8],因此引入时域平滑约束项,构造以下目标函数:

(5)

λ1和λ2都是正则化参数,式(6)右边第二项作为能量约束项,将逆问题的解约束为在时段k内全局能量最小的解;第三项作为时域平滑约束项,使解在相邻时刻间变化率最小.本文方法具有独立地对能量和时域平滑约束的性质:当λ1趋于零时,式(6)主要是时域平滑约束发挥作用;当λ2趋于零时,式(6)主要是能量约束发挥作用.λ2为零时本文方法等同于传统MNE方法,也就是说传统MNE方法是本文方法的一个特例.在求解时,通过适当地调整正则化参数λ1和λ2来达到能量约束和时域平滑约束之间的平衡,进而重建出能量小且时域平滑的信号.

Aliev B[9,10]引入类似本文的双参数正则化求解线性不适定算子方程时,从数学的角度证明了普适的双参数正则化解的唯一性、稳定性和收敛性.王文娟等[11]采用双参数正则化方法研究电导率反演成像中发现双参数正则化方法增强了反演的稳定性.另外,增加时域平滑约束后,重建信号对正则化参数的敏感度降低.Brooks等[8]在心电逆问题求解中通过实验发现,在正则化参数变化幅度相同的情况下,相比于仅有能量约束,增加时域平滑约束的双参数正则化方法重建的信号更稳定.因此本文方法具有良好的鲁棒性,下文介绍正则化参数选择策略和具体求解方法.

2.2 求解方法

首先根据Kronecker积的定义[12]将式(6)转化成如下形式:

(6)

(7)

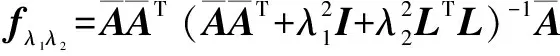
3 实验

3.1 仿真实验

在脑皮层选取两个活化位置,坐标分别为(-39.4982,-36.6656,56.8917)和(36.0071,-18.8000,58.9000),两个位置分别对应左脑和右脑感觉区.6ms时达到能量峰值的源信号被放置在(-39.4982,-36.6656,56.8917)处,19ms时达到能量峰值的源信号则被放置在(36.0071,-18.8000,58.9000)处,图2所示为未添加噪声信号时,在第6ms和第19ms时仿真信号在脑皮层和测量空间的成像图.

本文在用于脑电/脑磁信号分析的开源软件eConnectome[14,15]平台上完成了上述仿真数据的设计,并在此基础上对本文提出的方法进行了实验验证.具体地,我们将MEG仿真数据导入eConnectome后执行数据预处理(preprocessing),包括baseline correction (以1～4ms为基准线)和filtering(50Hz陷波滤波器),采用真实几何头模型和边界元方法求解正问题获取转换矩阵A,然后分别用式(2)传统MNE方法和式(6)时域平滑约束方法对经过预处理的数据进行脑磁源重建.

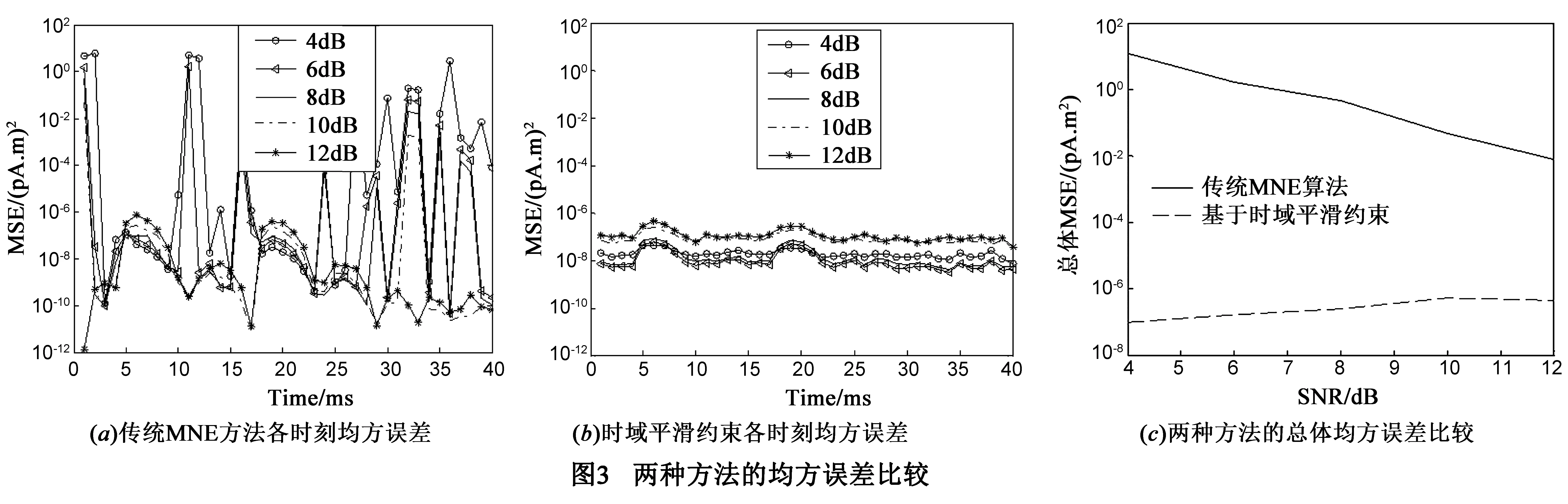
仿真实验结果考察两个方面:一是考察数据精确度参数均方误差,二是考察两个活化位置的估算信号与原始模拟信号的吻合情况.

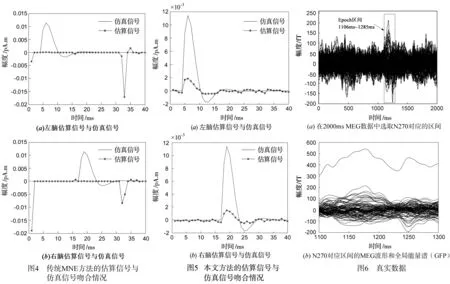
图4分别展示了脑皮层上两个活化位置(-39.4982,-36.6656,56.8917)和(36.0071,-18.8000,58.9000)采用传统MNE方法的估算信号和仿真信号之间的吻合情况.发现各个时刻间独立求逆使得解在时域上不规则振荡,且某些时刻与真实值相去甚远.图5显示引入双参数正则化增加时域平滑约束项后,估算信号基本复原了仿真信号变化趋势,而且分别在6ms和19ms处具有能量峰值.需要注意的是,估算信号的幅度小于真实信号,是因为式(9)中第二项是能量约束项,也就是说所求的估算信号是所有解中能量最小的解,这是重建算法本身决定的,MNE算法也存在同样的现象.

3.2 真实数据实验

本实验数据来自首都医科大学宣武医院神经内科对焦虑患者的认知实验数据集.研究发现,大脑对冲突信息进行加工时会在刺激出现后的270ms左右诱发负性相关电位,即认知电位冲突性负波N270[16].目前的研究认为由N270反映的认知冲突处理系统可能分散在大脑多个不同区域,但额内侧扣带回可能是该系统的重要组成部分[17].本实验通过分析一例焦虑患者的认知实验数据来验证时域平滑约束算法的有效性.实验为比较图形的颜色和形状,每一刺激对中随机呈现不同的颜色或形状让受试者判断,两个刺激各自持续500ms,两个刺激之间间隔200ms,每个刺激对间隔2s.

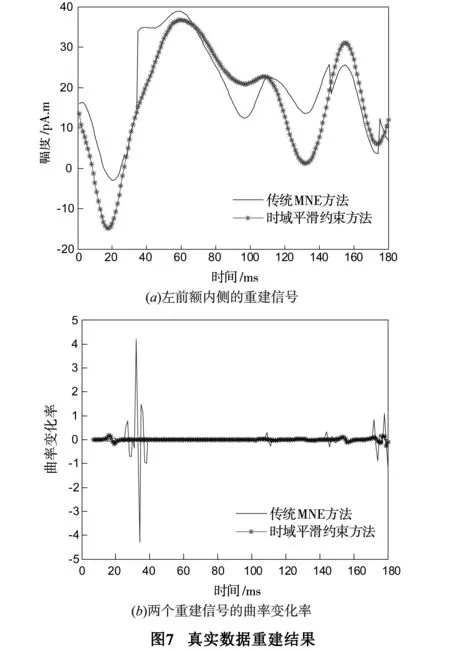
实验通过306导型号为ElektaNeuromag脑磁图仪采集MEG数据,分辨率为1000Hz.数据经过去眼电、滤波和基线校准等预处理步骤后,按照刺激对数叠加平均成时长为2000ms的MEG数据.为了定位N270认知冲突处理系统,选取1106ms～1285ms(对应N270时序段)为分析时程(epoch),如图6所示.以额内侧扣带回为兴趣区域,随机选择该区域内的某一位置,分别用式(3)传统MNE方法和式(11)时域平滑约束方法进行源时序信号重建.图7(a)所示为左前额内侧中心坐标为(-3.8603,59.3580,17.9440)处的重建结果.

参考图6(b)中的全局能量谱(GlobalFieldPower,GFP)曲线,本文提出的时域平滑约束方法较好地复原了源时序信号的形状,也成功地定位出两个能量峰值;而传统MNE方法在两个能量峰值处出现了不同程度的抖动,时域平滑性低于本文提出的时域平滑约束方法.我们还通过图7(b)所示的各时刻曲率变化率(curvaturevariability)定量比较了两个重建信号的平滑程度,传统MNE方法的总曲率变化率为0.1646,时域平滑约束方法的总曲率变化率为0.0640,也就是说,对于这个实验,在重建平滑能力上,时域平滑约束方法要比传统MNE方法强2.5倍以上.

由上述实验结果可知,本文提出的基于时域平滑约束的双参数MEG时序信号逆问题求解方法要优于传统MNE方法.

4 讨论

大脑对外部信息的反应是复杂的神经动力学过程,MEG逆问题的求解从MNE算法的提出虽然已有了很多发展,但仍有许多问题值得探索.本文从MNE算法出发,引入双参数混合正则化,通过时域平滑算子约束解空间,使得估算的时序源信号更符合神经信号定向传导的性质.这也为因果性脑网络[18]研究提供了更有效的分析工具.由于MNE算法的缺陷,时域约束估算值不可避免的有“模糊效应”[6],下一步的工作将在此基础上尝试减小这一效应,使得脑磁源重建结果更加精确.

[1]吴殿鸿,郭立文,等.脑物理学[M].哈尔滨:哈尔滨工业大学出版社,1995.39-41.

[2]肖庭延,于慎根,等.反问题的数值解法[M].北京:科学出版社,2003.18-30.

[3]Tikhonov A,Arsenin V.Solutions of Ill-posed Problems [M].Washington DC:Winston,1977.113-135.

[5]Fredric MH,Ivica K.神经计算原理[M].叶世伟,王海娟,译.北京:机械工业出版社,2007.7-11.

[6]Tian S T,Huang J Z,Shen H,Li Z.A two-way regularization method for MEG source reconstruction[J].The Annals of Applied Statistics,2012,6(3):1021-1046.

[7]Bolstad A,Veen B V,Novak R.Space-time event sparse penalization for magneto-/electroencephalography[J].NeuroImage,2009,46(4):1066-1081.

[8]Brooks D H,Ahmad G F,MacLeod R S,et al.Inverse electrocardiography by simultaneous imposition of multiple constraints[J].IEEE Trans.Biomed,1999,46(1):3-81.

[9]Alive B.Two-parameter regularization method for finding L-pseudo-solutions[J].Vestnik Moskov Univ Vychisl Mat Kibernet,1986,15(2):45-50.

[10]Alive B.Modification of the generalized discrepancy principle for L-pseudo-solutions in the degenerate case[J].Vestnik Moskov Univ Vychisl Mat Kibernet,1991,20(1):28-33.

[11]王文娟，Chris Farmer,等.双参数混合正则化方法及在电导率反演成像中的应用[J].地球物理学报，2011,54(8)：2154-2159. WANG Wen-juan， Farmer C,et al.A dual-parameter regularization method for electrical conductivity imaging[J].Chinese Journal of Geophysics,2011,54(8):2154-2159.(in Chinese)

[12]张贤达.矩阵分析与应用[M].北京：清华大学出版社,2004.107-117. ZHANG Xian-da.Matrix Analysis and Applications[M].Beijing:Tsinghua University Press,2004.107-117.(in Chinese)

[13]朱南海,赵晓华.基于遗传算法的Tikhonov正则参数优化计算[J].工程力学,2009,26(5):25-30. ZHU Nan-hai,ZHAO Xiao-hua.Optimal calculation of Tikhonov regularization parameter based on genetic algorithm[J].Engineering Mechanics,2009,26(5):25-30.(in Chinese)

[14]He B,Dai Y K,et al.eConnectome:A MATLAB toolbox for mapping and imaging of brain functional connectivity[J].Journal of Neuroscience Methods,2011,195(2):261-269.

[15]Dai Y K,Zhang W B,et al.Sourceconnectivity analysis from MEG and its application to epilepsy source localization[J].Brain Topography,2012,25(2):157-166.

[16]欧阳取平,王玉平.工作记忆对冲突性负波N270的影响[J].临床神经电生理学杂志,2008,17(6):323-327. OUYANG Qu-ping,WANG Yu-ping.The effects of working memory on the event-related potential N270[J].Journal of Clinical Electroneurophysiology,2008,17(6):323-327.(in Chinese)

[17]王玉平.事件相关电位N270的特性及本质[J].临床神经电生理学杂志,2002,11(4):247-248. WANG Yu-ping.The character and nature of the event-ralated potential N270[J].Journal of Clinical Electroneurophysiology,2002,11(4):247-248.(in Chinese)

[18]孙俊峰,洪祥飞,童善保.复杂脑网络研究进展—结构、功能、计算与应用[J].复杂系统与复杂性科学,2010,7( 4):74-90. Sun J F,Hong X F,Tong S B.A survey of complex brainnetworks:structure function computation and applications[J].Complex Systems and Complexity Science,2010,7(4):74-90.(in Chinese)

刘 婷 女,1986年出生于江苏赣榆,现为中科院苏州医工所硕士研究生.主要研究方向为脑电脑磁源成像.

E-mail：liutingcumt@163.com

戴亚康(通讯作者) 男,1982年出生于江苏常州,现为中科院苏州医工所研究员、博士生导师.主要研究方向为医学影像处理.在国内外发表学术论文30余篇.

E-mail:daiyk@sibet.ac.cn

杨莹雪 女,1986年出生于山东,现为首都医科大学宣武医院医师.主要研究方向为脑功能疾病的临床及电生理研究.

E-mail:yyx19861213@163.com

王玉平(通讯作者) 男,1961年出生于河北,现为首都医科大学宣武医院神经内科主任、北京市癫痫诊疗中心主任、脑功能疾病调控治疗北京市重点实验室主任、北京市脑重大疾病研究院癫痫病研究副所长.主要从事脑功能疾病的临床、电生理和基础研究,对癫痫、睡眠障碍、运动障碍病、认知障碍等临床问题有较深入的研究.在国内外发表学术论文280余篇.

E-mail:wangyuping01@sina.cn

An MEG Inverse Solver by Imposition of Temporal Smoothness Constraint

LIU Ting1,2,3,DAI Ya-kang1,YANG Ying-xue4,5,WANG Yu-ping4,5

(1.SuzhouInstituteofBiomedicalEngineeringandTechnology,ChineseAcademyofSciences,Suzhou,Jiangsu215163,China; 2.ChangchunInstituteofOptics,FineMechanicsandPhysics,ChineseAcademyofSciences,Changchun,Jilin130033,China; 3.UniversityofChineseAcademyofSciences,Beijing100049,China; 4.DepartmentofNeurology,XuanwuHospital,CapitalMedicalUniversity,Beijing100053,China; 5.BeijingKeyLaboratoryofNeuromodulation,Beijing100053,China)

The magnetoencephalography (MEG) inverse problem refers to the reconstruction of the neural activity of the brain from MEG measurements.A method to solve the MEG inverse problem employing temporal smoothness constraint is proposed under the assumption that time course of the source is smooth in time.Specifically,the temporal smoothness of the source was ensured by imposing a roughness penalty in the minimum norm estimate (MNE) data fitting criterion in the form of dual-parameter regularization.To select two tuning parameters,the generalized cross-validation criterion (GCV) was used.The inverse solutions were obtained as the linear combination of the one-parameter regularized solutions.We evaluated the proposed method by a synthetic example and a real data example.Compared with MNE,the proposed method can get smaller overall mean squared error (MSE) and smaller curvature variability.Moreover,the proposed method can reconstruct the shape of the time course of source better.

magnetoencephalography (MEG) time course;inverse problem;two-parameter regularization;temporal smoothness

2015-05-05;

2015-07-15;责任编辑:覃怀银

中国科学院百人计划基金项目;国家高技术研究发展计划(863计划)( No.2015AA020514);国家自然科学基金(No.61301042 );脑功能疾病调控治疗北京市重点实验室开放课题;江苏省自然科学基金(No.BK2012189);苏州市医疗器械与新医药专项基金(No.ZXY201426);中法“蔡元培”项目(No.201404490123)

TP301

A

0372-2112 (2016)12-2823-06

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.12.002