基于主成分分析的PM2.5的影响因素权重确定方法

董健卫，陈艳美，孟盼

（1.广东药科大学基础学院数学系，广东广州 510006；2.广东技术师范学院计算机科学学院，广东广州 510665）

基于主成分分析的PM2.5的影响因素权重确定方法

董健卫1，陈艳美2，孟盼1

（1.广东药科大学基础学院数学系，广东广州 510006；2.广东技术师范学院计算机科学学院，广东广州 510665）

以武汉市的空气数据为研究对象，通过主成分分析方法研究AQI中5项分指标及其对应污染物（含量）的权重大小.结果发现PM2.5的影响因素按权重大小分别为：二氧化氮，可吸入颗粒物，二氧化硫，一氧化碳，臭氧.该结果为减排PM2.5提供了可靠的理论依据.

PM2.5；AQI；主成分分析；权重大小

1 引言

AQI(Air Quality Index)新标准2016年1月1日已经开始在全国实施.与新标准同步还实施了《环境空气质量指数(AQI)技术规定(试行)》(HJ633—2012)［1］.AQI的分项监测指标为6个基本监测指标（二氧化硫SO2、二氧化氮NO2、可吸入颗粒物PM10、细颗粒物PM2.5、臭氧O3和一氧化碳CO等6项）.新标准中，首次将产生灰霾的主要因素——对人类健康危害极大的细颗粒物PM2.5的浓度指标作为空气质量监测指标［1］. PM2.5作为大气首要污染物，严重影响着人们的身体健康.

PM2.5的形成机理和过程比较复杂，可以分为一次颗粒物和二次颗粒物.徐小丽运用主成分分析法探讨西安市及伦敦市的空气质量监测指标中多种污染物与PM2.5的相关性，搜集的监测指标分别是：PM10、二氧化硫、二氧化碳、PM2.5、臭氧，根据这五个指标得到相关系数矩阵，再利用联合多重分型分析研究有限维分布族之间的差异分析，最终的结论表明：PM10与 PM2.5最相关［2］.阳其凯等［3］运用遗传算法与BP神经网络构建了PM2.5的发生演化模型，较为准确地预测了PM2.5的变化规律.关于PM2.5的相关因素分析，国外也有很多类似研究：Appel［4］、Senaratne［5］、Sisler和Malm［6］、Chen［7］等都对PM2.5相关因素做了分析.本文提出了一种基于主成分分析的PM2.5相关因素权重确定方法，为减排PM2.5提供了可靠的理论依据.

本文通过调查统计得出裂缝分布规律，基于统计学原理[]将路形和行车方向对裂缝的影响进行分析，并在已有研究成果的基础上分析裂缝的成因。

2 主成分分析

2.1 主成分分析原理

管网运行：GIS地理信息系统、GPA巡线系统、管网监测系统、水力模型系统、DMA分区管理系统、产销差系统等；

主成分分析［8］是把原来多个变量划为少数几个综合指标的一种统计分析方法.从数学角度来看，这是一种降维处理技术.

本文数据来自于武汉市环境保护局某检测站2013年1月1日至2013年8月26日的每日PM2.5数据：http://www.whepb.gov.cn/，部分显示如表1：

记原变量指标为x1，x2，…，xp，设它们降维处理后的综合指标，即新变量为z1，z2，z3，…，zm（m≤p）则：

综合对河套灌区农业可持续发展存在的问题与河套灌区农业资源承载力的分析结果，河套灌区水资源承载力和土地承载力均在可承载范围内，但是水资源承载力有所下降，已临近最大承载水平，并且还存在农用水资源量减少、水质污染等问题。土地资源承载力虽然逐渐提高，但是还存在建设用地占用耕地、土壤盐渍化、耕地质量下降等问题，因此，加强水土资源的保护与集约利用水平是河套灌区农业资源承载力提升的关键。

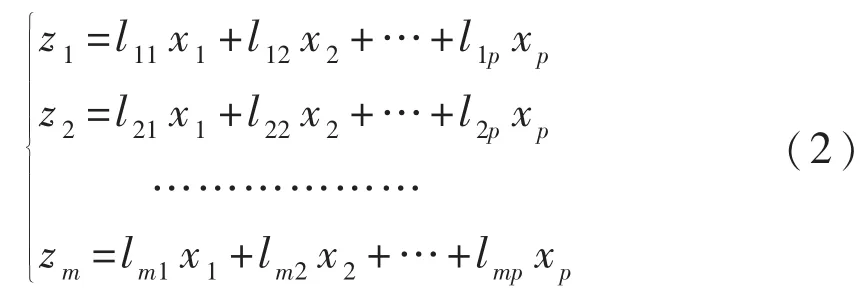
系数1ij的确定原则：

①zi与zj（i≠j，i，j=1，2，…，m）相互无关；

②z1是x1，x2，…，xp的一切线性组合中方差最大者，z2是与z1不相关的x1，x2，…，xp的所有线性组合中方差最大者；zm是与z1，z2，z3，…，zm-1都不相关的x1，x2，…，xp的所有线性组合中方差最大者.

电力建筑工程的质量问题与社会大众的生命财产安全有很大的关联，只有在将质量管理与控制的工作做好，才能真正的扩大社会大众的福利，对于社会的经济发展也作出了一份贡献。基于此，下文就电力建筑工程质量管理措施进行分析。

新变量指标z1，z2，z3，…，zm分别称为原变量指标x1，x2，…，xp的第1，第2，…，第m主成分.

从以上的分析可以看出，主成分分析的实质就是确定原来变量xj（j=1，2，…，p）在诸主成分zi（i=1，2，…，m）上的荷载lij（i=1，2，…，m；j=1，2，…，p）.

从数学上可以证明，它们分别是相关矩阵m个较大的特征值所对应的特征向量.

基于特征的单元信息描述模型虽能揭示单元信息的属性特征，却不能揭示单元信息之间的语义关系。因此需要构造单元信息本体模型，主要体现为单元信息本体语义关联。这种语义关联可以通过四个方面、两个层级来表示：四个方面包括“领域概念”“属性”“方法”“关系”这四个通用本体；两个层级是指单元信息内部和单元信息之间两个层次，通过关联得出单元信息的语义模型，如图1所示。

2.2 主成分分析的计算步骤

2.2.1 计算相关系数矩阵

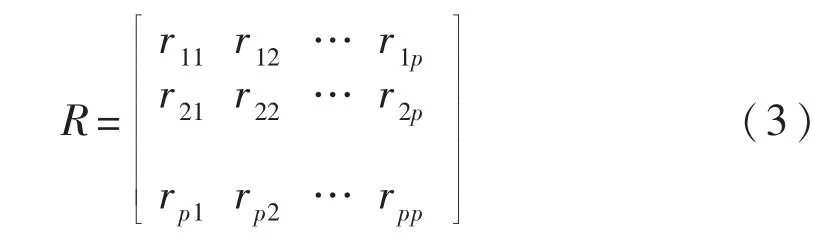
rij（i，j=1，2，…，p）为原变量xi与xj的相关系数，rij=rji，其计算公式为

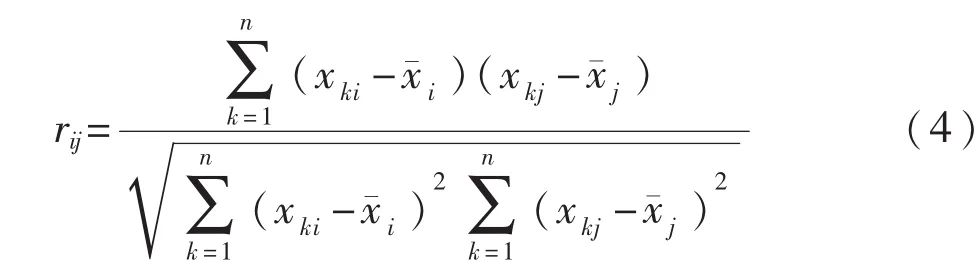
根据公式（7）用表5中的载荷数除以表4中第2列对应的特征根的开方.其中第一主成分所对应的特征值为3.1，第二主成分所对应的特征值为1.058.结果如表6：

东方宇轩心中的一段衷曲，七圣固然是不知，但大家的心思，也是宽慰的，来万花谷修身向道，固然可喜，修道的同时，聚天下英才少年而教育之，也是人生的至乐。一时大家点头含笑，将慈爱赞许的目光投向袁安、李离、上官星雨，好像目光里都要沁出蜜来，将三人梅子一般渍在其中。上官星雨悄悄地吐着舌头，袁安、李离也是松了一口气。只是，劳驾十位师父，冲暑犯露，晚上来到高高的摘星楼上，点灯费油，难道就是要通知我们三个白天的调皮捣蛋，并非是作弊，现在可以回去安心睡觉了吗？

2.2.3 计算主成分贡献率及累计贡献率

3.1 相关系数矩阵

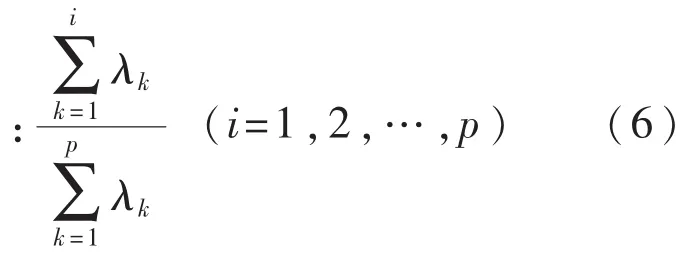
一般取累计贡献率超过80%的特征值，λ1，λ2，…，λm所对应的第1、第2、…、第m（m≤p）个主成分.

2.2.4 计算主成分载荷

针对传统压电能量俘获电路能量俘获能力低的问题,有研究人员提出了具有并联电感同步开关控制的压电能量俘获电路,如图3所示。

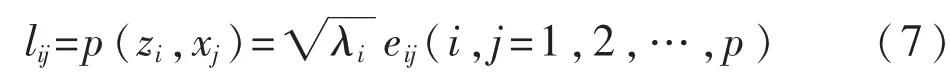
2.2.5 各主成分得分

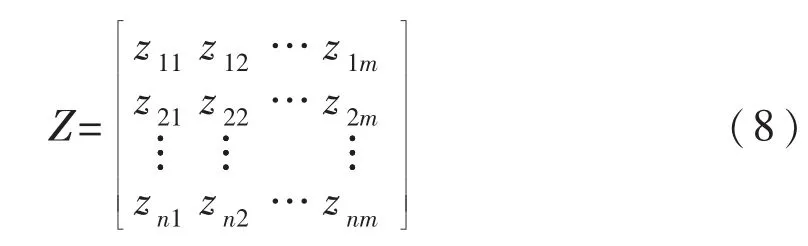
3 基于PCA的权重分析

累计贡献率

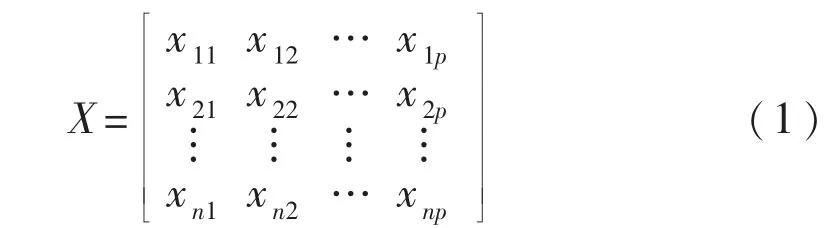
假定有n个样本，每个样本共有p个变量，构成一个n×p阶的数据矩阵：

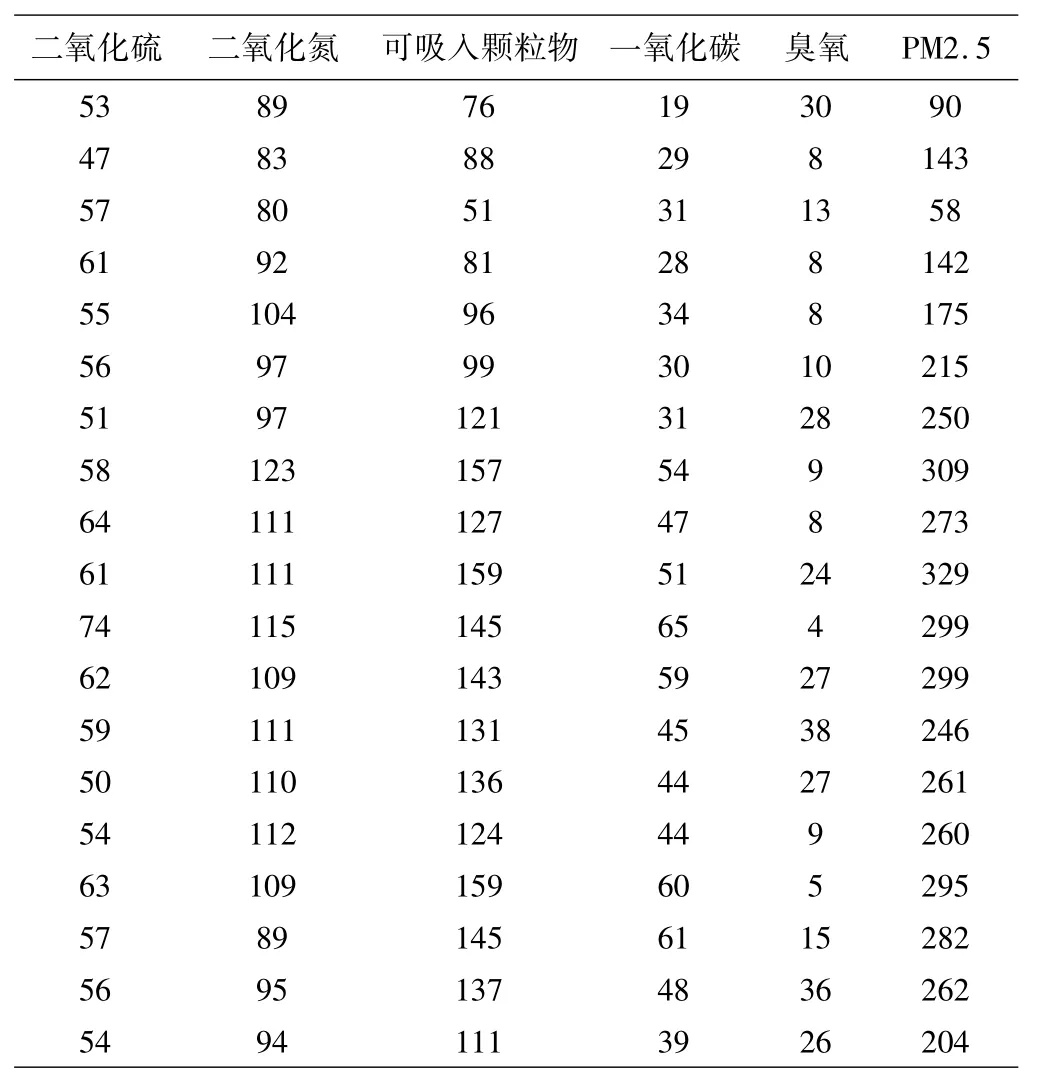
表1 摇原始数据

本文用SPSS17.0进行统计计算，通过相关系数公式(4)求得PM2.5与其他5项指标的相关系数如下表2：

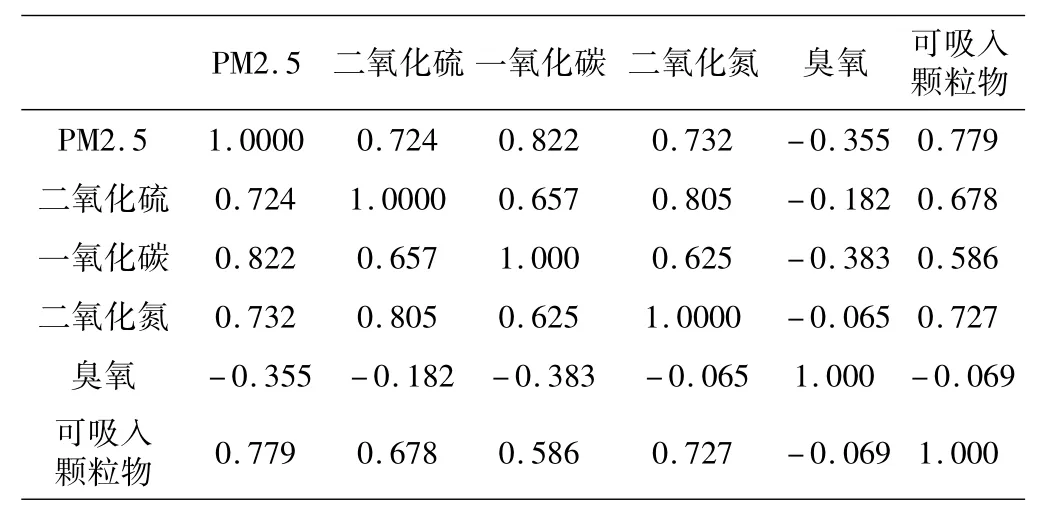
表2 摇相关系数矩阵

说明了PM2.5与二氧化硫、一氧化碳、二氧化氮、臭氧、可吸入颗粒物的相关性很强，因此二氧化硫、一氧化碳、二氧化氮、臭氧、可吸入颗粒物的相关浓度变化会引起PM2.5的浓度变化.

3.2 PCA结果分析

KMO和Bartlett球形检验结果如表3：

表3 摇KMO和Bartlett球形检验

解释的总方差如表4：

3.3 确定权重

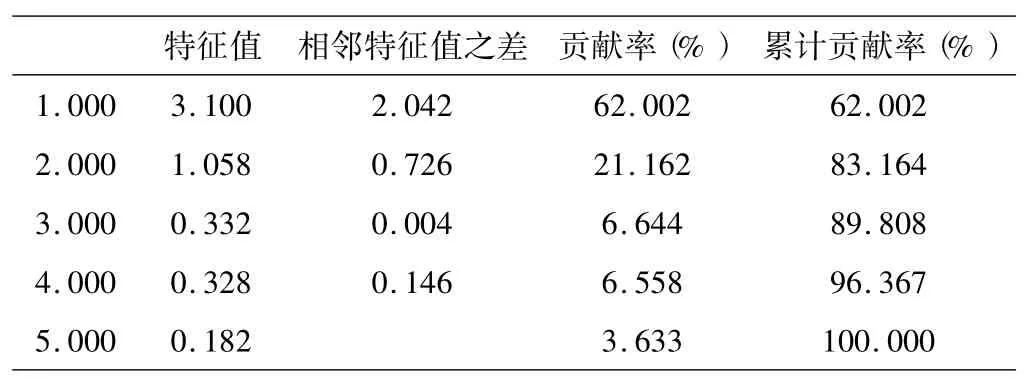
表4 摇相关矩阵的特征值及其累计贡献率

表4给出了各样本相关系数矩阵的特征值，相邻两个特征值之间的差，每个特征值所解释的方差比率和积累方差比率.前两个主成分对应的特征根大于1，而且前两个主成分的累计贡献率达到83.164%，大于80%，因此前2个主成分基本可以反映全部指标的信息，可以代替原来的5个指标（二氧化硫、一氧化碳、二氧化氮、臭氧、可吸入颗粒物）.

成份矩阵如表5：

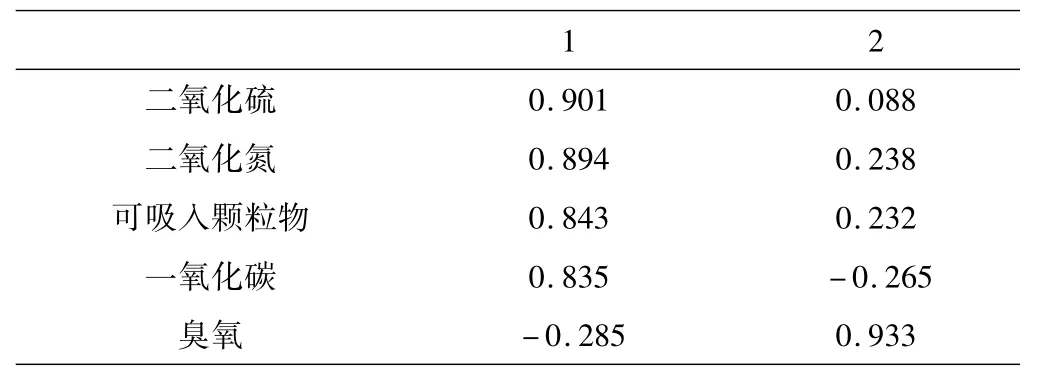
表5 摇成份矩阵

从表5可知第一主成分与第二主成分对原来指标的载荷数.

在本设计中采用Codevision AVR开发平台，充分发挥了AVR单片机对DS18B20的控制和读取，并且利用PID算法对被控对象进行控制，构成一个恒温抗扰动的反馈系统；结合简单的单总线技术，大大降低了硬件电路设计的复杂程度，在蔬菜种植中具有温控简单、操控方便、稳定性高、抗干扰能力强和维护成本低等优点。

三是稳步开展健康河湖创建活动。统筹规划分阶段工作目标和创建重点，突出河湖生态功能建设，强化河湖水域岸线管控，实施河湖生态健康修复提升工程，加快推进退渔还水、退田还水、控源截污、生态修复等综合治理措施，实现河流河道不脱流、水质不下降、岸线不萎缩、功能不衰减“四不”目标，湖泊保面（容）积、保水质、保功能、保生态、保可持续利用的“五保”目标，在此基础上，稳步改善提升，确保健康河湖建设取得实效。

经过五四个性解放的洗礼，以曾树生为代表的新一代女性在觉醒之后虽然面临着黑暗的社会环境，复杂的人生境遇，但觉醒后的新女性依然根据自己的本性做着自己的选择，进行着艰难的蜕变与成长。

用主成分分析确定权重有：指标权重等于以主成分的方差贡献率为权重，对该指标在各主成分线性组合中的系数的加权平均归一化.因此，要确定指标权重需要三个步骤：

A指标在各主成分线性组合中的系数；

B主成分的方差贡献率；

C指标权重的归一化；

3.3.1 指标在不同主成分线性组合中的系数的求法

2.2.2 计算特征值与特征向量

从调查的情况来看，目前华堂村的丝蚕生产仍采用一家一户在自家的土地上自己种桑自己养蚕的传统生产方式，生产技术水平仍十分原始落后，工效低，成本高，目前的产业链也不完整(嵊州原有两家缫丝厂，都已在几年前关闭，目前蚕茧需运往宁波市奉化县投售)，产品在市场上没有竞争力，目前桑田种植面积已很少，丝蚕生产整体呈不断萎缩态势，吸纳的劳动力十分有限.

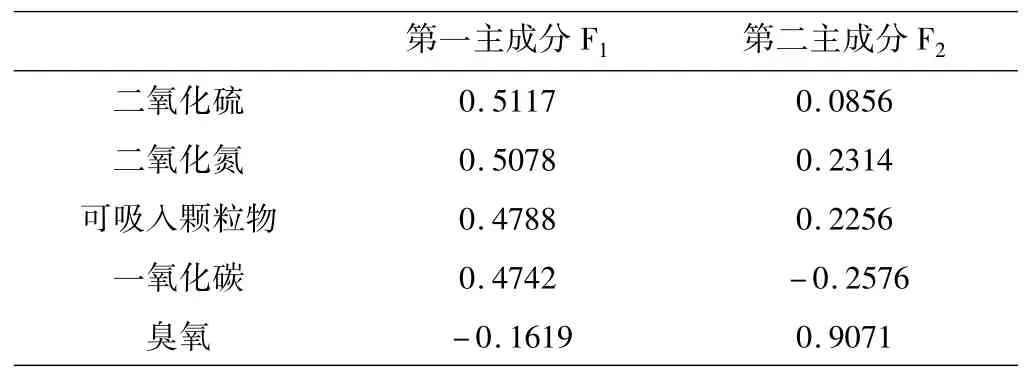
表6 摇各指标在两个主成分线性组合中的系数

由表6可得两个主成分的线性组合如下：F1=0.5117SO2+0.5078NO2+0.4788PM10+0.4742CO-0.1619O3

F2=0.0856SO2+0.2314NO2+0.2256PM10-0.2576CO+ 0.9071O3（9）

3.3.2 主成分的方差贡献率

方差贡献率越大，则该主成分的重要性就越强.因此，方差贡献率可以看成是不同主成分的权重.由于原有指标基本可以用前两个主成分代替，因此，指标系数可以看成是以这两个主成分方差贡献率为权重，对指标在这两个主成分线性组合中的系数做加权平均.由此得到的综合模型为：

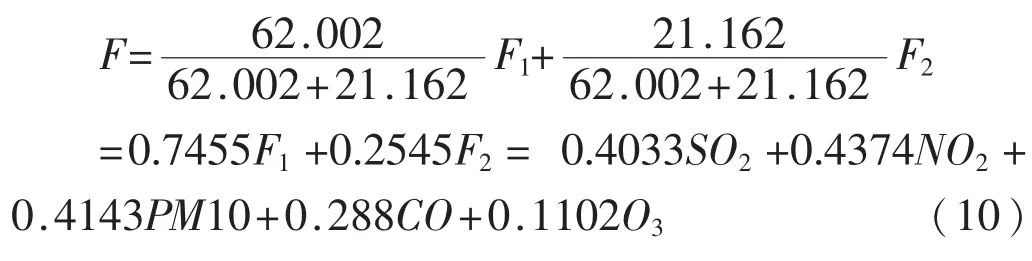
3.3.3 指标权重的归一化

医药企业研发风险主要来源于两方面：(1)药品研发环节程序多，且每一环节反复试验，存在极大不确定性；(2)研发活动的制度审批方面，受相关政策的干扰，新药审核不通过会阻碍研究进度并增大资金投入，从而产生研发风险和资金流风险。并且，还有外部宏观环境影响和内部竞争对手的压力、市场预期等。

由于所有指标的权重之和为1，因此指标权重需要在综合模型中指标系数的基础上归一化，F中的系数：FC=（0.4033，0.4374，0.4143，0.288，0.1102)，归一化公式为：

W=FC/sum（FC）=（0.2439，0.2646，0.2506，0.1742，0.0666）（11）

其中sum（FC）表示Matlab软件里面的向量求和函数.结果如表7：

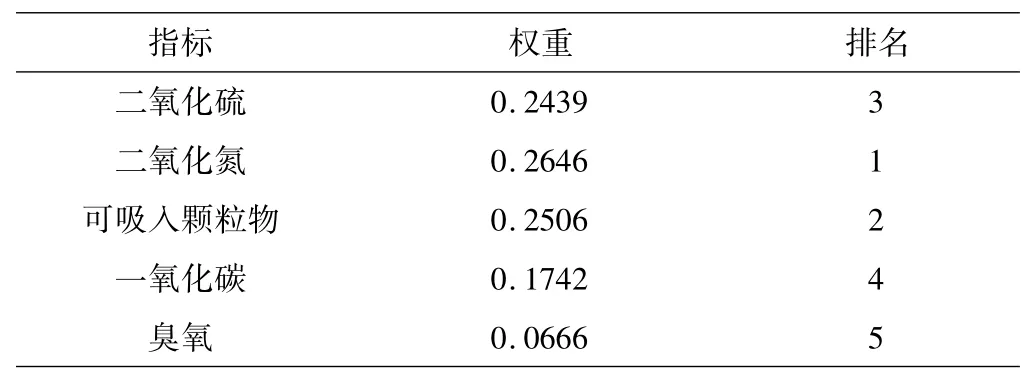
表7 摇PM2.5的各影响指标权重

因此，影响PM2.5的影响因素按权重大小分别为：二氧化氮，可吸入颗粒物，二氧化硫，一氧化碳，臭氧.二氧化氮主要来源于机动车排放的废气和燃放烟花爆竹；可吸入颗粒物通常来自在未铺沥青、水泥的路面上行使的机动车、材料的破碎碾磨处理过程以及被风扬起的尘土；二氧化硫主要来源于煤、石油等燃料的燃烧，工厂排放的废气等；一氧化碳主要来源于化石燃料的不完全燃烧和汽车的尾气等.所以要依次控制二氧化氮、可吸入颗粒物、二氧化硫、一氧化碳的排放，减少PM2.5的有效形成.

Egger′s检验(t=0.39，P=0.708)、Begg′s检验(Z=-0.27，P=0.784)和漏斗图(图5)的结果均提示，本篇Meta分析不存在发表偏倚。

4 结论

本文基于主成分分析方法，确定了AQI中 PM2.5的影响因素权重大小，为减排PM2.5提供了可靠的理论基础.研究认为，AQI监测指标中的二氧化硫（SO2）、二氧化氮（NO2）、一氧化碳（CO）是在一定环境条件下形成PM2.5前的主要气态物质.因此可以认为这些污染物在空气中通过物理和化学反应转化成了PM2.5，而水一般都是化学反应不可缺少的物质，所以空气湿度可能与PM2.5有关.因此，在PM2.5的相关因素分析中，可以进一步考虑分析空气湿度对PM2.5的影响，但是由于未采集到有关空气湿度的数据，所以本文未分析空气湿度对PM2.5的影响大小.

［1］环境空气质量指数（AQI）技术规定（试行）：中华人民共和国国家环境保护标准，HJ633-2012［S］.

［2］徐小丽.PM2.5变化趋势的多重分型分析研究［D］.安徽大学,2014.

［3］阳其凯，张贵强，张竞铭.基于遗传算法与BP神经网络的PM2.5发生演化模型［J］.2014（3）:15-18.

［4］Appel B R，Tokiwa J H，Hsu J，et al．Visibility as relatedtoatmosphericaerosolconstituents［J］．Atmospheric Environment,1985,19(9):1525-1534．

［5］Senartne I.Elemental composition in source identification of brown haze in Auckland，New Zealand［J］.Atmospheric Environment,2004,38(19):3049-3059．

［6］Sisler J F，Malm W C．The relative importance of soluble aerosols to spatial and seasonal trends of impaired visibility in the United States［J］．Atmospheric Environment，1994，28(5):851-862．

［7］Chen L W A，Chow J C，Doddridge B Q et al．Analysis of a summertime PM2.5 and haze episode in the mid－Atlantic region［J］．Journal of Air＆Waste Manage Association，2003，(53):946-956.

［8］杨淑菊.主成分分析在学生成绩评价中的应用［J］.数学的实践与认识,2012,42(16):103-112.

［责任编辑：刘昱］

The Determining Weight Method of the Influence Factors of PM2.5 Based on Principal Component Analysis

DONG Jianwei1,CHEN Yanmei2,MENG Pan1

(1.Department of Mathematics in School of Basic Courses,Guangdong Pharmaceutical University,Guangzhou
510006；2.School of computer science,Guangdong polytechnic Normal University,Guangzhou 510665)

To study the weight of the related indicators of PM2.5,this paper researches air data set of Wuhan city.By principal component analysis,the weight of the corresponding pollutants(content)of other five indicators in AQI is determined.The influence factors of PM2.5 according to weight size respectively are NO2,PMIO,SO2,CO and O3.Conclusion The results provide the reliable theory basis for the emission reduction of PM2.5.

PM2.5；AQI；Principal component analysis;Weight size

O 21

A

1672-402X（2016）11-0025-04

2016-06-25

广东省普通高校青年创新人才项目（董健卫，2014KQNCX137）；广东药科大学国家级大学生创新创业训练计划项目（林丽萍，201410573009）；国家自然科学基金项目(孟盼，11402057).

董健卫（1979-），男，山东泰安人，计算数学硕士，广东药科大学讲师.研究方向：数学模型及其应用，功能磁共振成像研究.