一类三次退化中心的极限环扰动

吴奎霖

（贵州大学数学系，贵阳 550025）

一类三次退化中心的极限环扰动

吴奎霖

（贵州大学数学系，贵阳 550025）

研究了一类三次退化中心的极限环分支问题.通过计算一阶Melnikov函数，得到了退化中心的周期环域在任意小扰动下分支出极限环的个数.

退化中心；极限环；Abel积分

平面微分系统的一个奇点E称为一个中心,如果E的一个邻域全由围绕它的周期轨道组成.这样最大的邻域称为中心的周期环域，通常记为P.对一般的可积微分系统

不妨设原点O（0，0）是系统（1）的一个中心，设H（x，y）是其首次积分.围绕O（0，0）的周期环域记为P：={γh：H（x，y）=h，h∈Σ}，其中Σ为h的极大区间，使得轨道γh：H（x，y）=h是系统（1）的周期轨道.孤立的周期轨道称为极限环，极限环个数问题的研究涉及到Arnold［1］提出弱化Hilbert第十六问题：考虑如下的哈密顿系统扰动

其中H是变量x，y的m次多项式，{（x，y）|H（x，y）=h，h∈（α，β）}定义了一族围绕中心的周期轨道，α、β是周期环域边界对应的哈密顿函数值，ε是充分小的正参数，其pn（x，y）和qn（x，y）是变量x、y的次数至多为n的多项式.问A-bel积分

孤立零点的最大个数Z（m，n）？Z（m，n）则是系统（2）ε=0的周期环域在n次小扰动下分支出极限环个数的最小上界.弱化Hilbert第16问题只对n=2［2］的情形得到了彻底的解决，即Z（2，2）= 2.本文考虑下面多项式系统的极限环分支问题

其中fk（x，y）和gk（x，y）是变量x和y的k次齐次多项式，μ为一实数，0＜ε＜1.文献［3］证明了下面微分系统

解析可积当且仅当它形式等价于系统（3）ε=0.系统（3）ε=0的首次积分为

当-1＜μ≤1时，原点O（0，0）是系统（3）ε=0的退化中心，其周期环域

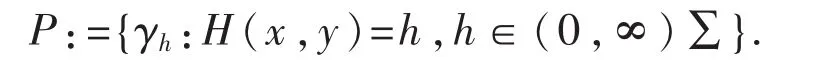
主要结论的证明

定理1的证明需用到下面类型的广义三角函数，其性质如下：

Csθ、Snθ是有相同周期的周期函数，设其周期为T.

要解决系统（3）ε=0的周期环域的极限环分支问题，首先需要研究下面这些Abel积分

由分部积分有

定理1的证明:我们分两种情况讨论，第一种情况：-1＜μ＜1，这时令

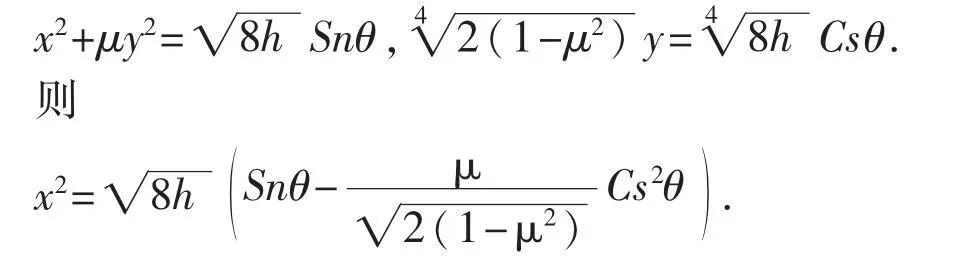
由式子（4）和（5）可知只需要考虑如下类型的Abel积分

其中

因此

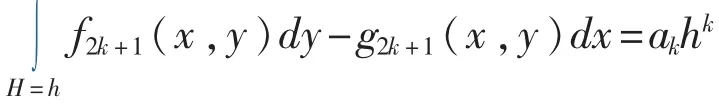
第二种情况：μ=1，这时系统（3）ε=0的首次积分为

其中ak是一个与参数k有关，与h无关的实数. Abel积分

综合以上两种情况讨论，定理1得证.

［1］V.I.Arnold,Arnold.s problems,Berlin Heidel-berg and PHASIS Moscow［M］,Springer-Verlag,2004.

［2］F.Chen,C.Li,A unified proof on the weak Hilbert 16th problem for n=2［J］,J.Diff.Eqns.,221（2）, 2006,309-342.

［3］A.Algaba,C.Garc1a,J.Gine,Analytic integrability for some degenerate planar systems［J］,Commun.Pure Appl.Anal.12（6）（2013）2797-2809.

［4］A.Buicã,J.Giné,J.Llibre,Bifurcation of limit cycles fromapolynomialdegeneratecenter［J］,Advanced Nonlinear Studies 10（2010）,597-609.

［5］J.Llibre,C.Pantazi,Limit cycles bifurcating from a degenerate center［J］,Mathematics and Computers in Simulation 120（2016）,1-11.

［责任编辑：刘向红］

Bifurcation of Limit Cycles from a Cubic Degenerate Center

WU Kuilin

（Department of Mathematics,Guizhou University,Guiyang,550025.）

In this paper,we deal with the bifurcation problem of limit cycles of a class of cubic degenerate centers.By computing the first order Melnikov function,we obtain that the number of limit cycles bifurcating from the period annulus of the cubic degenerate centers.

Degenerate center;Limit cycle;Abelian integral

O 123.4

A

1672-402X（2016）11-0006-02

2016-04-20

国家自然科学基金项目（编号：11301105，主持人：吴奎霖），贵州省科学基金基金［黔科合J字(2015) 2036号］

吴奎霖（1981-），男，贵州贵阳人，博士，贵州大学数学系教师.研究方向：常微分方程及应用.