解三角形的常见题型及其方法
程煌


【考纲分析】(1)正弦定理和余弦定理:掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题.(2)应用:能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题.
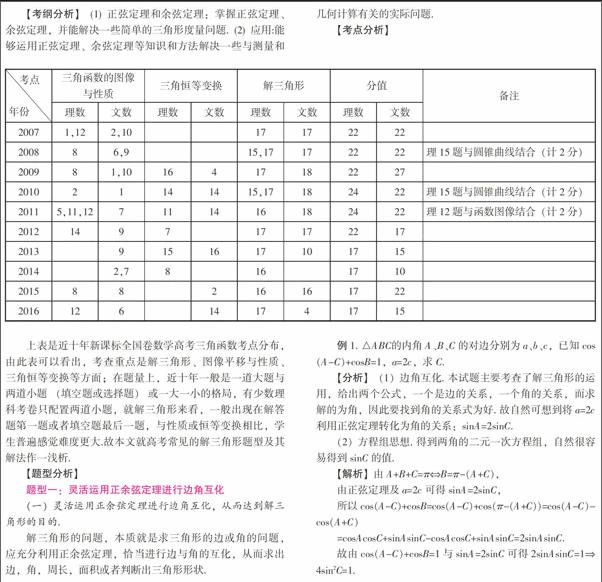
【考点分析】
上表是近十年新课标全国卷数学高考三角函数考点分布,由此表可以看出,考查重点是解三角形、图像平移与性质、三角恒等变换等方面;在题量上,近十年一般是一道大题与两道小题 (填空题或选择题) 或一大一小的格局,有少数理科考卷只配置两道小题,就解三角形来看,一般出现在解答题第一题或者填空题最后一题,与性质或恒等变换相比,学生普遍感觉难度更大.故本文就高考常见的解三角形题型及其解法作一浅析.
【题型分析】
题型一:灵活运用正余弦定理进行边角互化
(一)灵活运用正余弦定理进行边角互化,从而达到解三角形的目的.
解三角形的问题,本质就是求三角形的边或角的问题,应充分利用正余弦定理,恰当进行边与角的互化,从而求出边,角,周长,面积或者判断出三角形形状.
例1. △ABC的内角A、B、C的对边分别为a、b、c,已知cos(A-C)+cosB=1,a=2c,求C.
【分析】(1)边角互化. 本试题主要考查了解三角形的运用,给出两个公式,一个是边的关系,一个角的关系,而求解的为角,因此要找到角的关系式为好. 故自然可想到将a=2c利用正弦定理转化为角的关系:sinA=2sinC.
(2)方程组思想. 得到两角的二元一次方程组,自然很容易得到sinC的值.
【易错点】①方法一中由sin 2A=sin 2B直接得到A=B,其实考生忽略了2A与2B互补的情况,由于计算问题出错而结论错误.方法二中由c2(a2-b2)=(a2+b2)(a2-b2)不少同学直接得到c2=a2+b2,其实是考生忽略了a2-b2=0的情况,由于化简不当致误.
②结论表述不规范.正确结论是△ABC为等腰三角形或直角三角形,而不少考生回答为:等腰直角三角形.
题型二:正余弦定理与平面几何相结合,从而达到解三角形的目的.
这类题题目简洁明了,图形简单,是近几年高考的热点,但学生普遍反映三角函数中最害怕的就是这类题.没有直接告诉边角关系,而是给出几何图形,需要我们自己去寻找“突破口”,即分析应该从哪些三角形入手去寻找边角关系,从而达到目的.下面通过一题重点分析这类题型常见解法:
(三)数形结合思想求最值
例9. 在平面四边形ABCD中,∠A=∠B=∠C=75°,BC=2,则AB的取值范围是 .
【分析】此题直接边角互化求解很困难,特殊化是解决填空题的一种合情推理的方法,合理运用可以大大简化解题过程,当然,这个过程中不能忘记重要的数学思想方法:数形结合.但多数考生未能想到这一解法,这表明考生的合情推理能力的训练仍要加强.
【解析】如图所示,延长BA,CD交于E,平移AD,(1)当A,D,E重合时,AB最长,在△BCE中,∠B=∠C=75°,∠E=30° BC=2,由正弦定理可解得:BE=+. (2)当D与C重合时,AB最短,此时与AB交于F,在△BCF中,同理由正弦定理得:BF=-,故AB的取值范围为(-,+).
变式:在平面四边形ABCD中,∠BAD=135°,∠ADC=120°,∠BCD=45°,∠ABC=60°,BC=2,则线段AC长度的取值范围是 .
参考答案: [, 2].
题型四:解三角形在实际问题中的应用
例10. 如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点. 从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点得∠MCA=60°. 已知山高BC=100m,则山高MN=________m.
【分析】正余弦定理在解决实际问题中的应用学习的最终目的是为了应用于实际生活,遇到生活中的问题,我们可抽象出数学模型,然后应用定理去解决.应用数学知识解决问题的意识与能力是课程标准的明确要求,应用题是高考中的必考题型.三角函数是除概率之外出应用题的较好载体,在概率大题难以推陈出新时,三角函数就成为应用题的较好选择.三角函数应用题,一般是选择角为变量,通过建立三角函数作为目标函数来处理问题.三角函数应用题还可以与其他知识,如导数与不等式等结合,扩大考查的深度与广度,这一单元的复习,三角函数应用题应作为重点来对待.
此题实际可以抽象为一个立体几何模型,分析题意发现已知角很多,但是边长只有BC的长,所以应该从BC所在的三角形入手,解出AC的长,从而在△ACM中,可解出AM的长度从而在Rt△AMN中解出MN的长度.
【解析】在Rt△ABC中,BC=100,∠CAB=45°,所以AC=100,在△ACM中,∠MAC=75° ∠MCA=60°,由正弦定理可得AM=100,在Rt△AMN中,可解得MN=150.
【总结】解三角形相关问题,主要是正弦定理和余弦定理的应用.正弦定理是一个关于边角关系的连比等式,在运用此定理时只要知道其比值或者等量关系就可以通过约分达到解决问题的目;运用余弦定理时,要注意整体思想的运用以及与基本不等式的综合应用;对于给出条件是边角关系混合在一起的问题,一般应运用正弦定理和余弦定理,要么把它统一为边的关系,要么把它统一为角的关系,再利用三角形的有关知识,三角恒等变形方法,代数恒等变形方法等进行转化化简,从而得出结论.解决正弦定理和余弦定理的综合应用问题,应注意根据具体情况引入未知数,运用方程思想解决问题.在解决问题的时候,不要忘记数形结合、函数与方程的数学思想,在处理客观题训练时,可适当合情推理.
责任编辑 徐国坚

