“极限思想”巧妙破解超越函数图像客观题

曾光

综观高考数学试题中，经常会出现一道超越函数的图像客观题，难度中等，但往往令同学们感到比较头疼.为什么呢？原因是这类题没什么规律可循，题风十分飘忽，不好捉摸.如2016年全国高考1卷理数第7题.题目如下：

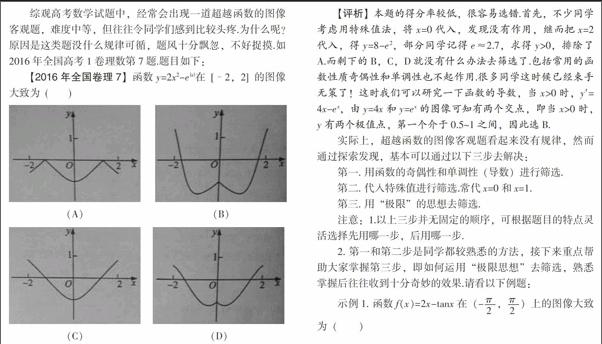
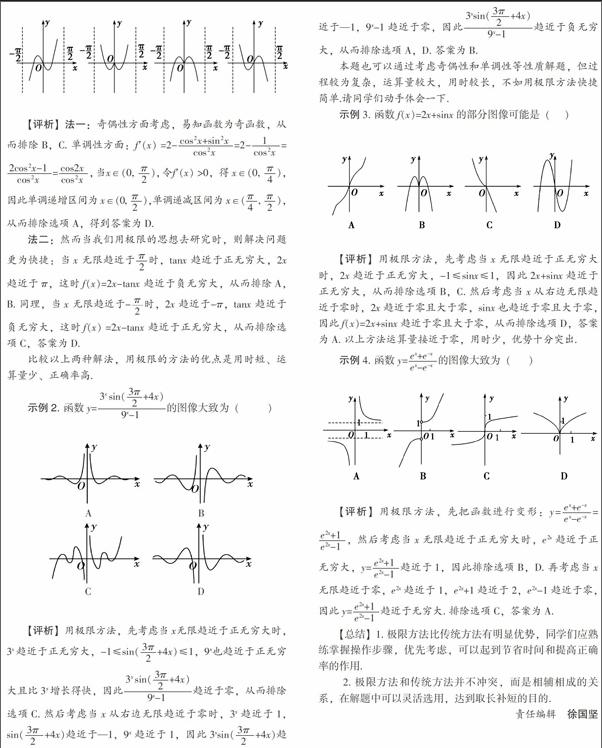
【2016年全国卷理7】函数y=2x2-e|x|在[–2，2]的图像大致为（ ）

【评析】本题的得分率较低，很容易选错.首先，不少同学考虑用特殊值法，将x=0代入，发现没有作用，继而把x=2代入，得y=8-e2，部分同学记得e≈2.7，求得y>0，排除了A.而剩下的B，C，D就没有什么办法去筛选了.包括常用的函数性质奇偶性和单调性也不起作用.很多同学这时候已经束手无策了！这时我们可以研究一下函数的导数，当x>0时，y′=4x-ex，由y=4x和y=ex的图像可知有两个交点，即当x>0时，y有两个极值点，第一个介于0.5～1之间，因此选B.

实际上，超越函数的图像客观题看起来没有规律，然而通过探索发现，基本可以通过以下三步去解决：

第一. 用函数的奇偶性和单调性（导数）进行筛选.

第二. 代入特殊值进行筛选.常代x=0和x=1.

第三. 用“极限”的思想去筛选.

注意：1.以上三步并无固定的顺序，可根据题目的特点灵活选择先用哪一步，后用哪一步.

2. 第一和第二步是同学都较熟悉的方法，接下来重点帮助大家掌握第三步，即如何运用“极限思想”去筛选，熟悉掌握后往往收到十分奇妙的效果.请看以下例题：

示例1. 函数f（x）=2x-tanx在（-，）上的图像大致为（ ）

【评析】法一：奇偶性方面考虑，易知函数为奇函数，从而排除B，C. 单调性方面：f′（x） =2-=2-==，当x∈（0， ），令f′（x） >0，得x∈（0， ），因此单调递增区间为x∈（0， ），单调递减区间为x∈（， ），从而排除选项A，得到答案为D.

法二：然而当我们用极限的思想去研究时，则解决问题更为快捷：当x 无限趋近于时，tanx 趋近于正无穷大，2x趋近于π，这时f（x）=2x-tanx 趋近于负无穷大，从而排除A，B. 同理，当x 无限趋近于-时，2x 趋近于-π，tanx 趋近于负无穷大，这时f（x） =2x-tanx 趋近于正无穷大，从而排除选项C，答案为D.

比较以上两种解法，用极限的方法的优点是用时短、运算量少、正确率高.

示例2. 函数y=的图像大致为（ ）

【评析】用极限方法，先考虑当x无限趋近于正无穷大时，3x 趋近于正无穷大，-1≤sin（+4x）≤1，9x也趋近于正无穷大且比3x 增长得快，因此趋近于零，从而排除选项C. 然后考虑当x从右边无限趋近于零时，3x趋近于1，sin（+4x）趋近于—1，9x趋近于1，因此3xsin（+4x）趋近于—1，9x-1趋近于零，因此趋近于负无穷大，从而排除选项A，D. 答案为B.

本题也可以通过考虑奇偶性和单调性等性质解题，但过程较为复杂，运算量较大，用时较长，不如用极限方法快捷简单.请同学们动手体会一下.

示例3. 函数f（x）=2x+sinx的部分图像可能是（ ）

【评析】用极限方法，先考虑当x无限趋近于正无穷大时，2x趋近于正无穷大，-1≤sinx≤1，因此2x+sinx趋近于正无穷大，从而排除选项B，C. 然后考虑当x从右边无限趋近于零时，2x趋近于零且大于零，sinx也趋近于零且大于零，因此f（x）=2x+sinx趋近于零且大于零，从而排除选项D，答案为A. 以上方法运算量接近于零，用时少，优势十分突出.

示例4. 函数y=的图像大致为（ ）

【评析】用极限方法，先把函数进行变形：y==，然后考虑当x无限趋近于正无穷大时，e2x趋近于正无穷大，y=趋近于1，因此排除选项B，D. 再考虑当x无限趋近于零，e2x趋近于1，e2x+1趋近于2，e2x-1趋近于零，因此y=趋近于无穷大. 排除选项C，答案为A.

【总结】1. 极限方法比传统方法有明显优势，同学们应熟练掌握操作步骤，优先考虑，可以起到节省时间和提高正确率的作用.

2. 极限方法和传统方法并不冲突，而是相辅相成的关系，在解题中可以灵活选用，达到取长补短的目的.

责任编辑 徐国坚