一道力学题的趣味变形

彭立君●

湖南省岳阳市第一中学(414000)

一道力学题的趣味变形

彭立君●

湖南省岳阳市第一中学(414000)

原型题 如图1所示，竖直放置的圆环最高点为P，从P点向圆环上各点搭建三条光滑的直轨道PA、PB、PC，物体从P点静止释放，分别沿轨道运动到A、B、C三点经历的时间为tA、tB、tC，比较tA、tB、tC的大小关系.

分析 取物体沿PC杆运动研究，设PC杆与竖直方向直径夹角位θ，则a=gcosθ，s=2Rcosθ

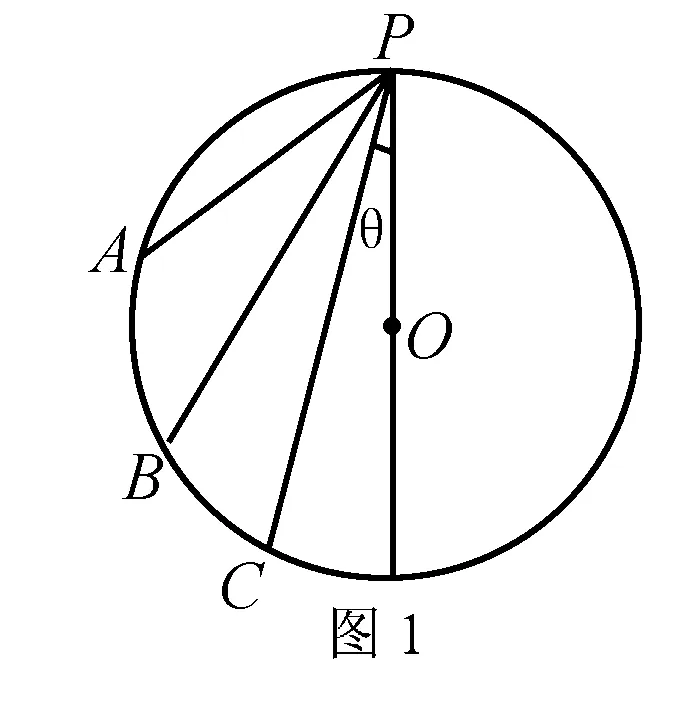
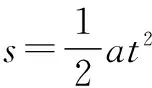
时间与θ角无关，则tA=tB=tC

结论：从竖直放置的圆环顶点沿光滑弦到达圆环上各点的时间相等(从竖直放置的圆环上各店沿光滑弦到达圆环最等低点的时间)

变型1：如图2所示，从倾角为θ的斜面外一点P搭建一系列光滑轨道到达斜面上，欲使物体从P点静止出发到达斜面的时间最短，问轨道与竖直方向的夹角α为多少？

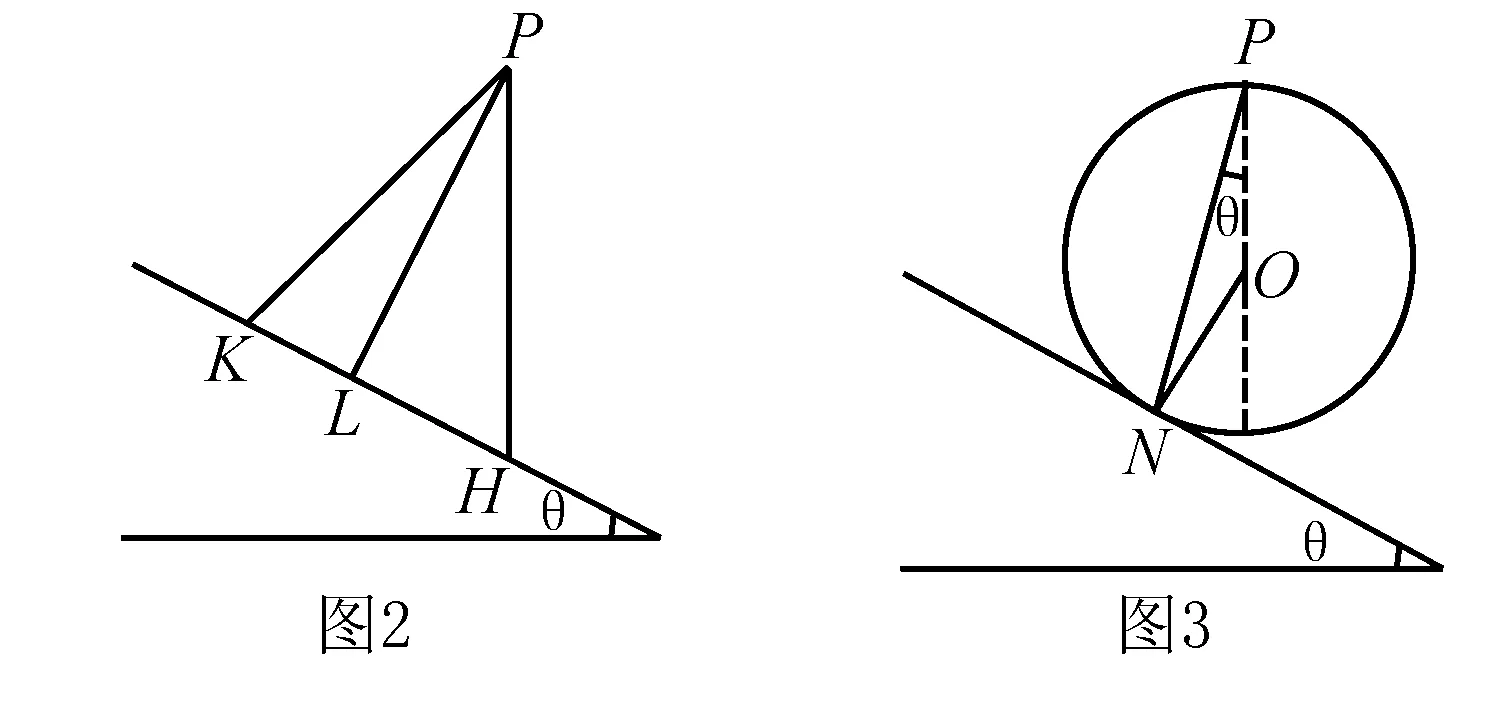
分析 根据上题结论，可以过P点作一圆，P为圆的最高点，圆与斜面相切于一点M，则物体从P到M点的时间小于物体到达斜面上任意一点的时间.

如图3所示，沿PN轨道到达斜面上N点时间最短.

根据几何关系易知，ON与竖直方向的夹角为θ，即

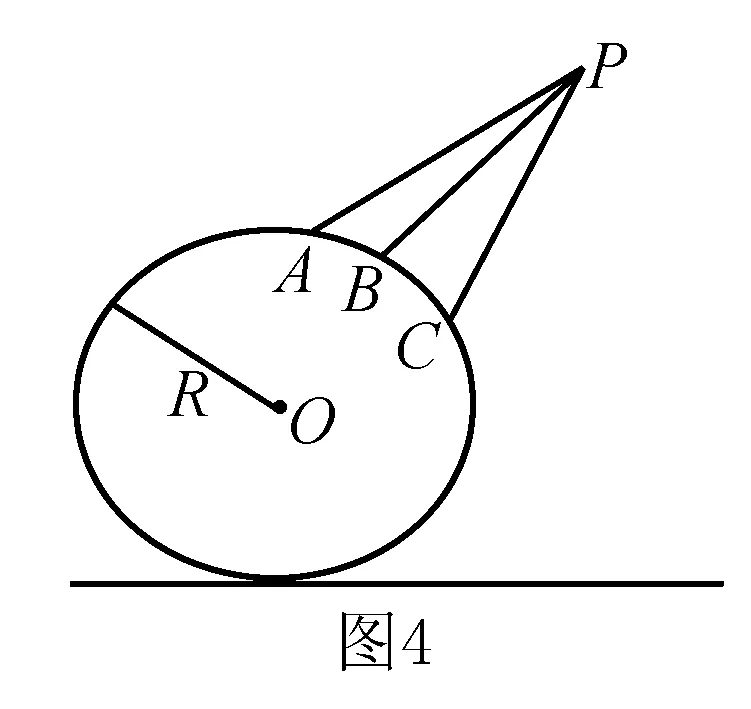
变形2：如图4所示，从圆外一点P向圆环上各点搭建光滑的轨道，使物体从P点沿轨道静止出发到达圆环上，求物体到达圆环的最短时间.(已知：圆环半径为R，P点到地面的距离为H，PO之间的水平距离为d)

这是一道竞赛备用题，直接处理有较大的难度，但是，有了上面的问题铺垫之后，就变成了简单的作图题了.

分析 根据上面的结论，过P点作一圆，P为圆的最高点，圆与圆环O相切与M点，则物体从P点到M点的运动时间最短.

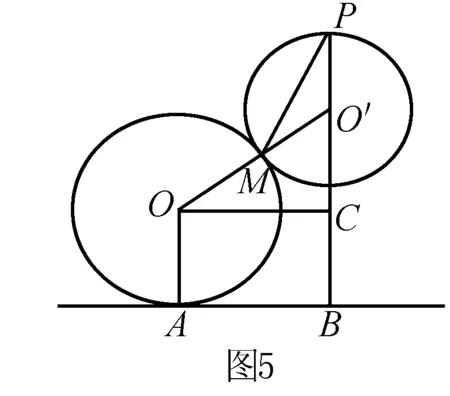
图5所示，设圆O′半径为r，由图中几何关系知：

在ΔOO′C中，有

OC2+O′C2=O′O2

即d2+(H-R-r)2=(R+r)2

从P到达M点的时间等于从P点沿竖直直径做自由落体的时间.

变形3：如图6所示，从竖直放置的圆环上左侧一点P向右侧偏P点下方搭建三条光滑轨道PA、PB、PC，物体从P点静止出发到达A、B、C三点的时间分别为tA、tB、tC，比较tA、tB、tC的大小关系.

粗看跟上面三个问题有较大的区别，能否转换成类似问题求解呢？

分析：根据上面的问题我们知道，竖直圆环上最高点沿光滑弦到圆环上的一点的时间等于物体从最高点沿竖直直径到达最低点的时间.PA、PB、PC是否对应了三个不同的圆半径呢？以P为竖直平面内的圆的最高点分别过A、B、C作圆，比较对应圆半径的大小，就可以知道运动时间的长短.

如图7所示，过P点作圆O的直径，交圆O于P′，过P点作竖直线PM，连接AP′并延长于PM交于A′，则ΔPAA′为直角三角形，即PA′为ΔPAA′的外接圆直径，且A′P在竖直方向，P为外接圆的最高点.

同理可作PB′、PC′，易知PA′>PB′>PC′，即tA>tB>tC

题目之间粗看有较大的差别，仔细思考却是很有联系，复杂的问题也是由简单的问题经过组合、叠加、条件变换等方法变形而来.

G632

B

1008-0333(2016)34-0057-01