椭圆中长度最值问题的解法

张 丽●

江苏省南通市如皋市第二中学(226500)

椭圆中长度最值问题的解法

张 丽●

江苏省南通市如皋市第二中学(226500)

圆锥曲线中的椭圆毫无疑问是高考的最热门考点，每年都会有考查，而椭圆中的长度最值也是椭圆问题中的热点问题.椭圆中要求的长度无非就是某一线段的长度或者是几条线段的长度之和，只要灵活地运用解题方法是可以解决这一问题的.

椭圆定义;函数法;三角转换

在圆锥曲线的题目中最让学生头疼的莫过于庞大的计算量，不仅会给解题带来不便还会影响解题的准确率.本文介绍的三种不同方法致力于简化繁琐的计算过程，实现问题的简单化，对症下药，帮助学生跨越这段鸿沟.

一、运用椭圆定义求长度最值

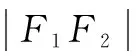
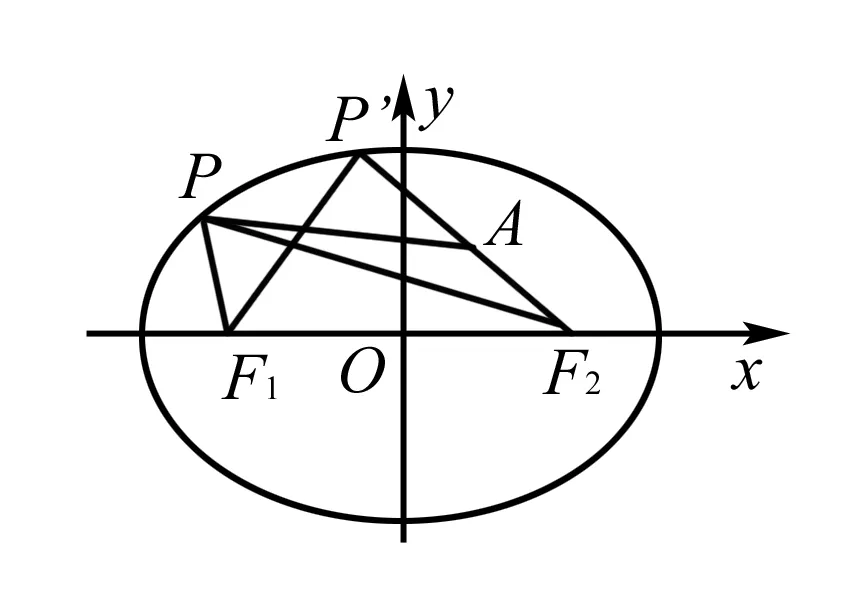
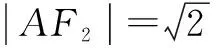
本题中利用了三角形两边之和大于第三边这一大家熟知的结论，进而根据椭圆定义巧妙解题.在实际做题中，类似于此种结论对我们解距离最值类问题有很大的帮助，学生应该多多练习，实现对知识的全面掌握.

二、函数法解决长度最值

函数法就是利用题目中的数量以及等式关系建立一个函数，通过学过的有关函数方面的相关知识(例如利用函数的单调性、二次函数的知识等)进行解题.

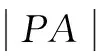
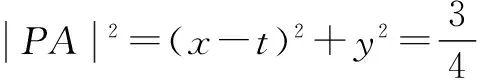
本题中由于点A位置的不确定性，使得最小值的取值也不同，是较为开放的题目.学生在解答此类问题时按照求二次函数的最值方法去做即可，不必为多解情况感到担忧.同时在解此类问题时需要注意的是消去y后自变量的取值范围.

二、将长度最值用点参法转化为三角最值

点参法的实质就是通过三角换元，将长度问题转化为求三角最值的问题，实现了问题的化简，从而解决了长度最值问题.

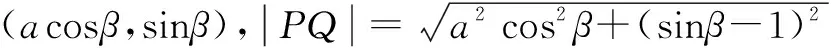
通过引参用参对代数运算进行化简是此种方法的最终目的，也是此种方法的优势所在.不光在椭圆中可以采用此种方法，不同的圆锥曲线都有其自己的参数表达式，灵活适当地运用此种方法，确实会给我们的解题带来便利.

纵观全文，三种方法的介绍从不同角度阐释了椭圆中长度最值问题的解法，其中既有数形结合思想的体现也有转化思想的应用，对于高中的数学思想学生需要在做题中加以总结，并且打开自己的思维，从不同的角度去思考问题，实现自身解题能力的提升.

G632

B

1008-0333(2016)34-0021-01