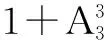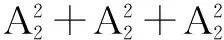两例排列组合的映射题
王苏文●
浙江省诸暨市浬浦中学(311824)
两例排列组合的映射题
王苏文●
浙江省诸暨市浬浦中学(311824)
在平时的排列组合练习中,经常遇到一些求解映射个数相关的问题.映射题具有一定的抽象性,是学生学习时的一个难点.下面通过两例对排列组合中映射个数问题作些探讨,以此帮助解决排列组合中的映射题.
例1 已知集合A={1,2,3,4},B={-1,0,1},
①从集合A到集合B的映射有多少个?
②从集合B到集合A的映射有多少个?
③若集合C={a,b,c,d},则A到C上的一一映射共有多少个?
④集合A中的元素1一定对应于集合B中的元素0,这样的映射有多少个?
⑤集合B中的元素在集合A都有原象,这样的映射有多少个?
⑥有且只有集合B中的元素-1才有两个原象,这样的映射有多少个?


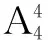
④由于集合A中的元素1一定对应于集合B中的0,则相当于新集合M={2,3,4}到B={1,0,-1}有多少个映射.所以,满足题意的有33=37个不同的映射.


此例主要围绕映射的基本概念出发,没有涉及多个限制条件的问题,相对而言比较简单.
例2 (1)已知集合A={1,2,3,4,5},B={-1,0,1},在f:A→B的映射中,满足条件f(1)≤f(2)≤f(3)≤f(4)≤f(5)的映射共有多少个?
变式题 已知两个实数集合A={1,2,3,4,5}与B={-1,0,1},若映射f:A→B,使得B中每个元素都有原象,且f(1)≤f(2)≤f(3)≤f(4)≤f(5),则这样的映射共有多少个?
(2)已知集合A={1,2,3,4,5},B={-1,0,1},在f:B→A的映射中,满足条件
f(-1) 思考 将其中一个“<”改成“≤”呢? (3)已知集合A={1,2,3},B={-1,0,1},在f:A→B的映射中,满足条件 f(-1)+f(1)+f(0)=0的映射共有多少个? (4)已知集合A={1,2,3},B={-1,0,1},在f:A→B的映射中,满足条件f(1)+f(2)=f(3)的映射共有多少个? (5)已知集合A={-1,0,1},B={5,6,7,8,9},在f:A→B的映射中,满足x+f(x)+xf(x)的值为奇数的映射共有多少个? (4)分析 根据题意可用两种思路进行求解. (5)分析 由于集合A中的元素可分为两类:奇数与偶数.故可按照奇偶性来分. 总之,在解决与映射有关的排列组合问题时,要把握一点即对于集合A中的任何一个元素,在集合B中都有唯一的元素和它对应,由于集合A中的元素往往不止一个,故常采用分步计数原理进行求解较多. G632 B 1008-0333(2016)34-0005-02