软土地层矩形顶管隧道工后地表沉降计算方法研究

魏 纲， 李志渊， 王 彬

(浙江大学城市学院土木工程系， 浙江 杭州 310015)

软土地层矩形顶管隧道工后地表沉降计算方法研究

魏 纲， 李志渊， 王 彬

(浙江大学城市学院土木工程系， 浙江 杭州 310015)

矩形顶管隧道施工会使周围土体产生扰动，进而引起超孔隙水压力，导致施工结束后继续产生固结沉降，对周围环境造成危害。采用Peck公式计算矩形顶管在施工阶段引起的地表沉降量； 运用应力释放理论和应力传递理论，推导出矩形顶管隧道周围土体中任意一点的超孔隙水压力计算公式，采用分层总和法计算土体初始超孔隙水压力消散引起的工后地表固结沉降量；二者叠加得到工后地表总沉降量。提出固结开始t时刻的地表总沉降量计算方法，研究了地表沉降和地表沉降速率随时间的变化规律。算例分析结果表明： 本文方法计算得出的沉降速率在施工结束后3个月内最大，之后迅速减小； 横向地表固结沉降曲线和总的地表沉降曲线均符合正态分布规律。

矩形顶管； 初始超孔隙水压力； 工后地表沉降； 软土地层

0 引言

随着城市发展，地面交通拥堵已成为普遍现象，因此发展地下空间变得极为重要。矩形顶管法作为地下隧道的一种施工工法，有着空间利用率大、对周边环境影响小等优点；但矩形顶管隧道在顶进结束后会继续产生地表沉降，且随时间增加而增大，进而危害到周围建(构)筑物。因此，对矩形顶管施工引起的工后地表沉降的研究具有重要意义。

目前关于矩形顶管施工引起土体变形的研究方法主要有： 经验法[1]、理论计算法[2]、数值模拟法[3-7]和实测数据分析法[8-11]等。经验法中： 林强强[1]证明Peck公式可用于计算矩形顶管施工期间的地表沉降。理论计算法中： 王日东[2]采用随机介质理论得出矩形顶管推进引起的三维土体变形计算方法。数值模拟法中： 文献[3-7]均模拟了不同工况下矩形顶管施工引起的土体变形。实测数据分析法中： 温锁林[8]通过施工现场实测土体沉降、孔隙水压力和土体水平位移，得到施工对周边环境的影响规律；施文捷等[9]通过现场实测数据，探讨了矩形顶管施工过程中周边水土压力及地表变形随时间的变化规律；郭亮[10]通过施工现场监测土体变形，得到土体沉降的变化规律；邓长茂等[11]通过对上海软土地层中3个大截面矩形顶管施工实例分析，发现矩形顶管推进引起地表变形具有一般规律性。综上所述，目前对矩形顶管施工期间引起地表沉降的研究较多，但未见对工后地表沉降的研究，也不清楚Peck公式是否适用于工后地表沉降计算。因此，有必要对矩形顶管引起的工后地表沉降作进一步研究。

本文借鉴盾构隧道工后地表沉降的计算方法，提出矩形顶管隧道施工引起的周围土体初始超孔隙水压力计算方法，采用分层总和法计算每层土体中由于超孔隙水压力消散引起的固结沉降量，叠加施工阶段的地表沉降量，得到工后总的地表沉降量。通过算例分析，研究工后地表横向和纵向沉降以及地表沉降速率的变化规律。

1 土体初始超孔隙水压力计算方法

1.1 研究思路及假定

本文研究对象为软土地区矩形顶管施工引起的工后地表沉降(包括施工期间沉降和固结沉降)。在研究土体初始超孔隙水压力前，作以下假设： 1)本文中出现的初始超孔隙水压力为土体中最大超孔隙水压力； 2)土体开挖应力释放导致初始超孔隙水压力的产生，且隧道周围土体的应力释放率大小相等； 3)矩形顶管隧道一侧视为挡土墙。

本文借鉴盾构隧道施工产生的土体超孔隙水压力计算方法： 通过计算出隧道水平线处起拱点(图1中A1点)土体超孔隙水压力大小以及该点围压大小，二者相除得到应力释放率；再根据应力释放理论，得出隧道周围土体初始超孔隙水压力大小及分布规律。

由于矩形和圆形在几何性质上存在不同，起拱点位置不一致。在矩形顶管中可假设矩形隧道一侧为挡土墙；根据库仑土压力理论，图1中A2点(即墙趾点)为挡土墙滑动破坏面起拱点，因此选择A2点作为矩形顶管隧道初始超孔隙水压力的计算点(以下简称隧道角点处)。

1.2 矩形顶管隧道周围土体初始超孔隙水压力计算

1.2.1 隧道围压的计算方法

矩形顶管隧道的围压受力模式见图2。

图1 盾构隧道与矩形顶管隧道初始超孔隙水压力计算点

Fig. 1 Calculation points of initial excess pore water pressure in shield tunnel and rectangular pipe jacking tunnel

H为矩形顶管隧道顶部覆土埋深；h为矩形顶管隧道外部高；l为矩形顶管隧道外部宽；θ为计算点与隧道水平夹角，取值为-π/2～π/2；P1为上覆土压力；P2为侧面土压力；P3为隧道自身重力。

图2 矩形顶管隧道受力示意图[12]

Fig. 2 Force diagram of rectangular pipe jacking tunnel[12]

上部应力：σ1=γH。

(1)

侧向应力：σ2=γK0(H+h/2-ltanθ/2)。

(2)

下部应力：σ3=γH+P3。

(3)

式(1)—(3)中：γ为土体重度，由于有多层土体，采用加权平均得到；K0为静止土压力系数。

1.2.2 隧道角点处土体初始超孔隙水压力计算方法

根据文献[13]，隧道角点(图1中A2点)处土体的初始超孔隙水压力

(4)

Δσr=Ps-(K0σ0′+u0)；

(5)

Δσθ=σ0′+u0-Ps；

(6)

Δσz=μ(Δσr+Δσθ)；

(7)

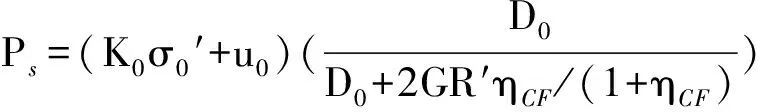
(8)

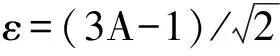
1.2.3 土体应力释放率计算方法

由式(3)和式(4)计算得到隧道角点(图1中A2点)处的土体初始超孔隙水压力值(U0′)和水土压力值(σ3)，则土体应力释放率α=U0′/σ3。

1.2.4 隧道周围土体初始超孔隙水压力计算

矩形顶管隧道周围的土体初始超孔隙水压力，可以通过隧道围压乘以土体应力释放率α得到。由于矩形隧道存在转角，周围土体中隧道侧面超孔隙水压力与顶部及底部超孔隙水压力区域中间存在4个过渡区域，这在圆形隧道中是没有的。矩形顶管隧道周边土体初始超孔隙水压力示意图见图3。

图3 矩形顶管隧道周边土体初始超孔隙水压力示意图

Fig. 3Sketchdiagramofinitialexcessporewaterpressureofsurroundingrocksofrectangularpipejackingtunnel

本文提出过渡区域可假定由一组对数螺旋线ρ=r0exp(a0θ′)组成，其中ρ和θ′为对数螺旋线函数的变量，分别代表超孔隙水压力大小和该位置处与水平方向的夹角；r0、a0为对数螺旋线参数，可以通过曲线两端已知的初始超孔隙水压力大小联立计算得到。由此可计算得到4个过渡区域(图3中虚线区域)中土体的初始超孔隙水压力。

1.3 土体扰动范围确定

本文在文献[14-15]的研究基础上提出了土体初始超孔隙水压力分布范围的具体计算方法。以隧道右半横截面为例，矩形顶管施工扰动范围如图4所示，本文参考文献[15]的计算方法，可确定A、B、C点的具体位置。

图4 矩形顶管隧道施工扰动范围

(9)

(10)

(11)

1.4 分布范围内任一点土体初始超孔隙水压力计算

本文假定： 1) 由于矩形顶管开挖引起土体卸荷扰动，适用朗肯主动土压力理论，因此土体超孔隙水压力扩散面(边界)与水平面夹角为β=45°+φ/2。超孔隙水压力由隧道开挖卸荷引起，而不是地表加载引起，因此超孔隙水压力是从隧道边界向外侧传递并扩散。2) 由于沿隧道顶进方向距离较长，因此简化为平面应变问题，该方向在计算中长度均取1m。3) 沿隧道边缘任一点垂直方向，土体内各点的初始超孔隙水压力值从隧道边界向外侧发生衰减。4) 土体超孔隙水压力扩散面上应力均匀分布。5) 周边土体各点的初始超孔隙水压力不受其余处影响，仅由该点相对应的与隧道相邻处初始超孔隙水压力U0传递。

以隧道横截面为例，本文超孔隙水压力传递模型见图5。

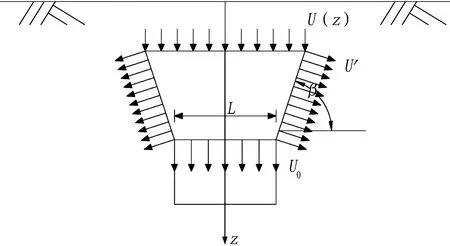
图5 隧道周围土体超孔隙水压力向四周传递示意图

Fig. 5Sketchdiagramoftransmissionofexcessporewaterpressureofsurroundingrocks

1)隧道拱顶上方土体初始超孔隙水压力计算。令隧道顶部向上传递应力的土体宽度为L。魏纲[17]在盾构隧道超孔隙水压力计算中提出令(H0+L)/(H0+2R)=0.7，故

L=1.4R-0.3H0。

(12)

式中：H0为盾构隧道的覆土埋深；R为盾构隧道外半径，在矩形顶管隧道中，本文提出将等效半径R′(1.2.2节中已给出取值方法)代入式中计算更合适。

隧道顶部土体的初始超孔隙水压力值U0=αPθ=90°，其中Pθ=90°为隧道顶部围压值。由竖向受力平衡推导得出侧面应力

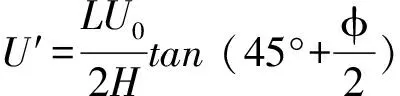
(13)

距离地面z深度处的土体竖向初始超孔隙水压力

(14)

2)隧道下方土体超孔隙水压力计算。推导得到扰动边界以上距离f处土体的竖向初始超孔隙水压力

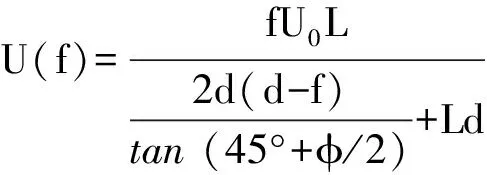
(15)

式中d为隧道到扰动边界的距离。

3)隧道侧向土体超孔隙水压力计算。以隧道水平轴线上的侧向土体为例，推导得到隧道侧向距离k处的土体初始超孔隙水压力

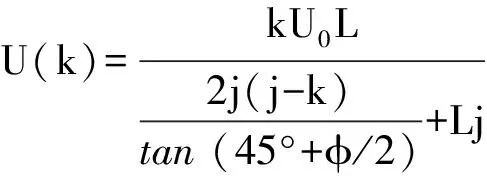
(16)

式中j为隧道到扰动边界的距离。

2 工后地表长期沉降计算

矩形顶管隧道施工引起的最终总的地表沉降量S由施工期间地表沉降S1和最终地表固结沉降量S2组成，则

S=S1+S2。

(17)

工后地表沉降计算模型及坐标方向如图6所示。

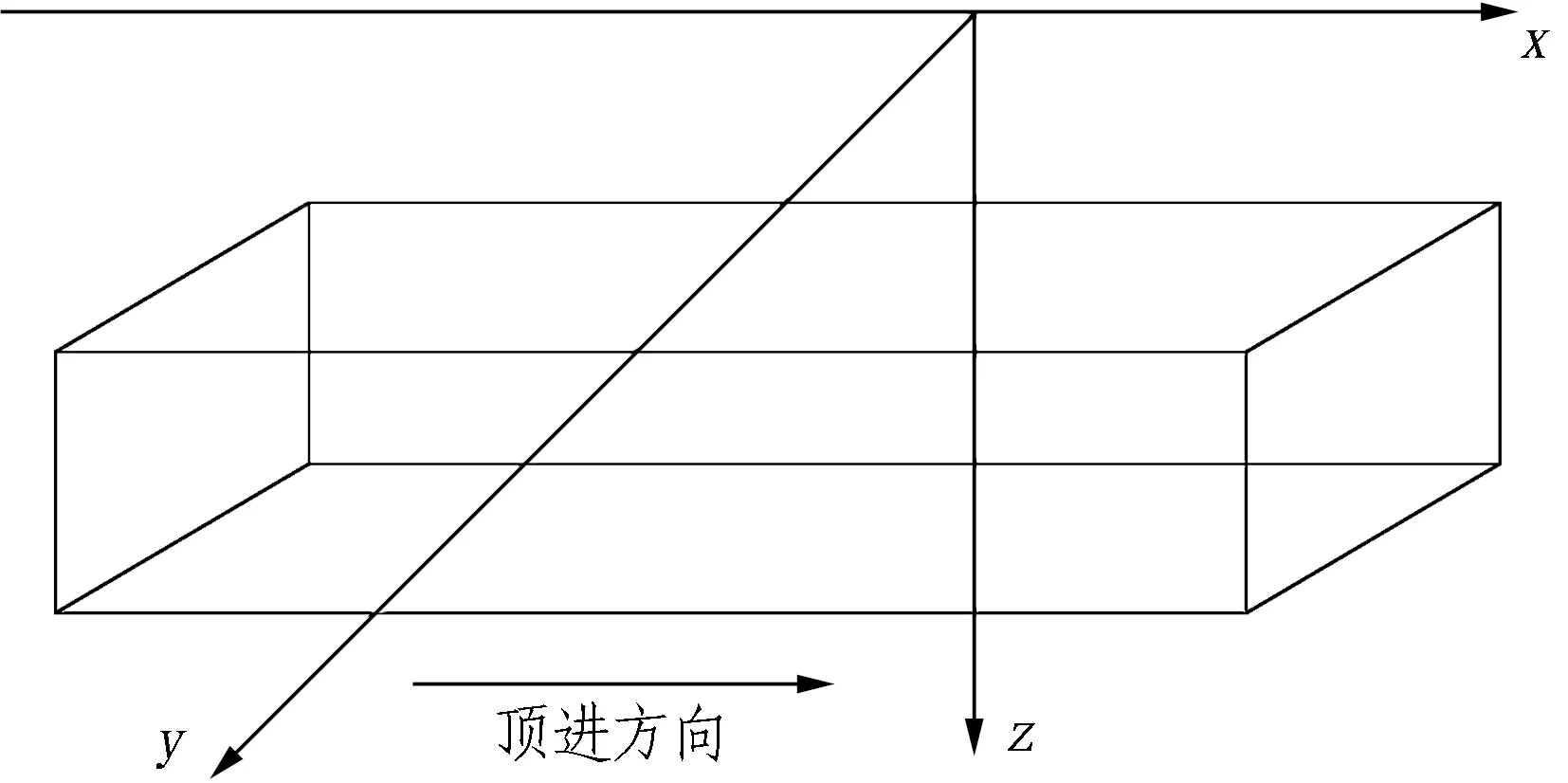
图6 工后地表沉降计算模型简图

Fig. 6Sketchdiagramofcalculationmodelofpost-constructiongroundsurfacesettlement

2.1 施工引起地表沉降计算

林强强[1]证明Peck公式[18]可用于计算矩形顶管施工期间的地表沉降S1，即：

(18)

式中： Vloss为隧道单位长度土体损失量，Vloss=hlη，其中η为土体损失率； i为施工阶段的地表沉降槽宽度系数； y为计算点距隧道轴线的横向水平距离。

2.2 施工结束后地表最终固结沉降计算

采用分层总和法单向压缩基本公式，可计算得到矩形顶管施工引起的地表最终固结沉降量S2。为简化计算，作出以下假设： 1) 由于各层土的附加应力不易于确定，假定土质均匀； 2) 土质参数(压缩模量)采用加权平均参数。

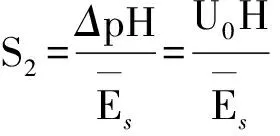
(19)

2.3 地表沉降随时间的变化规律

土体固结t时间之后的地表总沉降量S(y，t)可表示为

S(y,t)=S1(y)+S2(y,t)=S1(y)+UzS2(y)。

(20)

式中： S2(y，t)为土体固结t时间之后的固结沉降量； Uz为固结度，因为土体初始超孔隙水压力近似为三角形分布，可根据文献[19]中图2-52中曲线(3)得到，其中土体固结时间因数(竖向)

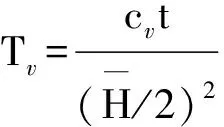
(21)

通过研究沉降速率和时间之间的关系，可以得出单位时间内地表沉降量的变化。由不同时间t所取的Uz计算得到地表沉降量S(y，t)。令第i个计算点的时间为ti，i从1开始取值。则ti时间对应的地表沉降量为S(y,ti),ti+1时间的地表沉降量为S(y,ti+1)。令(ti+1-ti)时间段内的地表沉降量为ΔS(y,ti)，则地表日沉降速率:

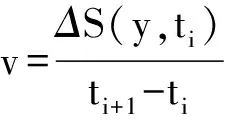
(22)

3 算例分析

3.1 工程概况及计算过程

以上海市轨道交通六号线浦电路车站3号出入口矩形顶管工程[1]作为实际案例，进行算例分析。顶管隧道长42 m，共28个管节，每个管节长1.5 m，内部尺寸为高3.36 m、宽5.24 m、厚度tc=0.5 m，即h=4.36 m、l=6.24 m。覆土埋深H=7.2 m，地下水位0.56 m。土体各参数取值见表1。

表1 土体参数取值

地表沉降槽宽度系数i的取值，参考文献[20]中的相关研究：i=k(H+0.5h)，黏性土中k值分布范围为0.37～0.66，本文取k=0.37，得到i=3.47m。土体初始有效应力可通过总应力减去土体中静止孔隙水压力得到。在该算例中，隧道角点处土体初始有效应力为110 kPa。

根据式(4)—(8)可计算得到隧道角点处的土体初始超孔隙水压力为33.01 kPa，由式(3)计算得到该点处隧道围压为106.05 kPa，二者相除得到应力释放率α=31.12%。隧道顶部围压为124.63 kPa，即可得到该点处初始超孔隙水压力为38.79 kPa。

根据1.4节的计算方法，计算得到隧道周围土体扰动范围内的土体初始超孔隙水压力等值线图，见图7。根据分层总和法单向压缩基本公式，对地表横向最终固结沉降量进行计算。如图7所示，土体共被划分为8层，每层层厚为2 m，其中底层厚度为1.95 m。y分别取0、1、2、4、6、10、14 m。

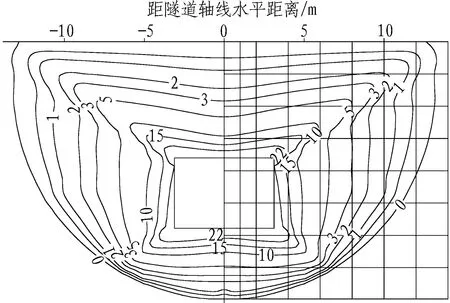
图7 土体初始超孔隙水压力等值线图(单位： kPa)

Fig. 7 Contour map of initial excess pore water pressure of soil (kPa)

根据式(19)可以计算得到横向地表最终固结沉降值，再利用式(20)可以计算得到地表总沉降量随时间的变化值，最后由式(22)可以计算得到隧道轴线上方地表总的日沉降速率随固结时间变化值。

3.2 计算结果分析

图8为隧道轴线上方地表工后总沉降计算值与实测数据[1]对比图。由于顶管全部贯通后实测工作结束，导致该断面工后仅实测25 d，没有后期数据。如图8所示，采用本文方法所得计算结果与实测数据比较吻合且趋势一致，验证了本文方法的可靠性。

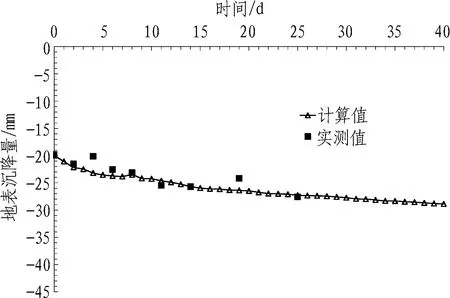
图8 隧道轴线上方地表总沉降计算值与实测数据对比

Fig. 8 Comparison between calculated total ground surface settlements above tunnel axial line and measured total ground surface settlements

图9为隧道轴线上方地表总沉降计算值随时间变化曲线。由图9可知，初始阶段地表沉降增长速度较快，地表沉降随时间成凸曲线增长；后期地表沉降随时间开始近似成线性增长，地表沉降速率逐渐减小至趋近不变。

图10为横向地表总沉降随时间变化曲线。由图10可知，随着时间增长，横向地表总沉降逐渐增大，但沉降曲线大致符合正态分布规律。

图11为由式(22)计算得到的隧道轴线上方地表总的日沉降速率随固结时间变化曲线。由图11可知，工后前3个月地表沉降速率最大，随后半年内沉降速率的变化曲率迅速减小，并在接下来的数年里沉降速率保持稳定。

图9 隧道轴线上方地表总沉降计算值随时间变化曲线

Fig. 9 Curve showing relationship between calculated total ground surface settlement above tunnel axial line and time

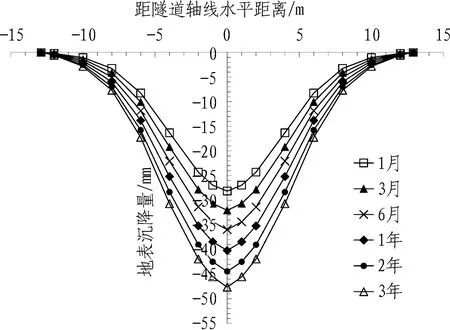
图10 横向地表总沉降随时间变化曲线

Fig. 10 Curve showing relationship between total horizontal ground surface settlement and time

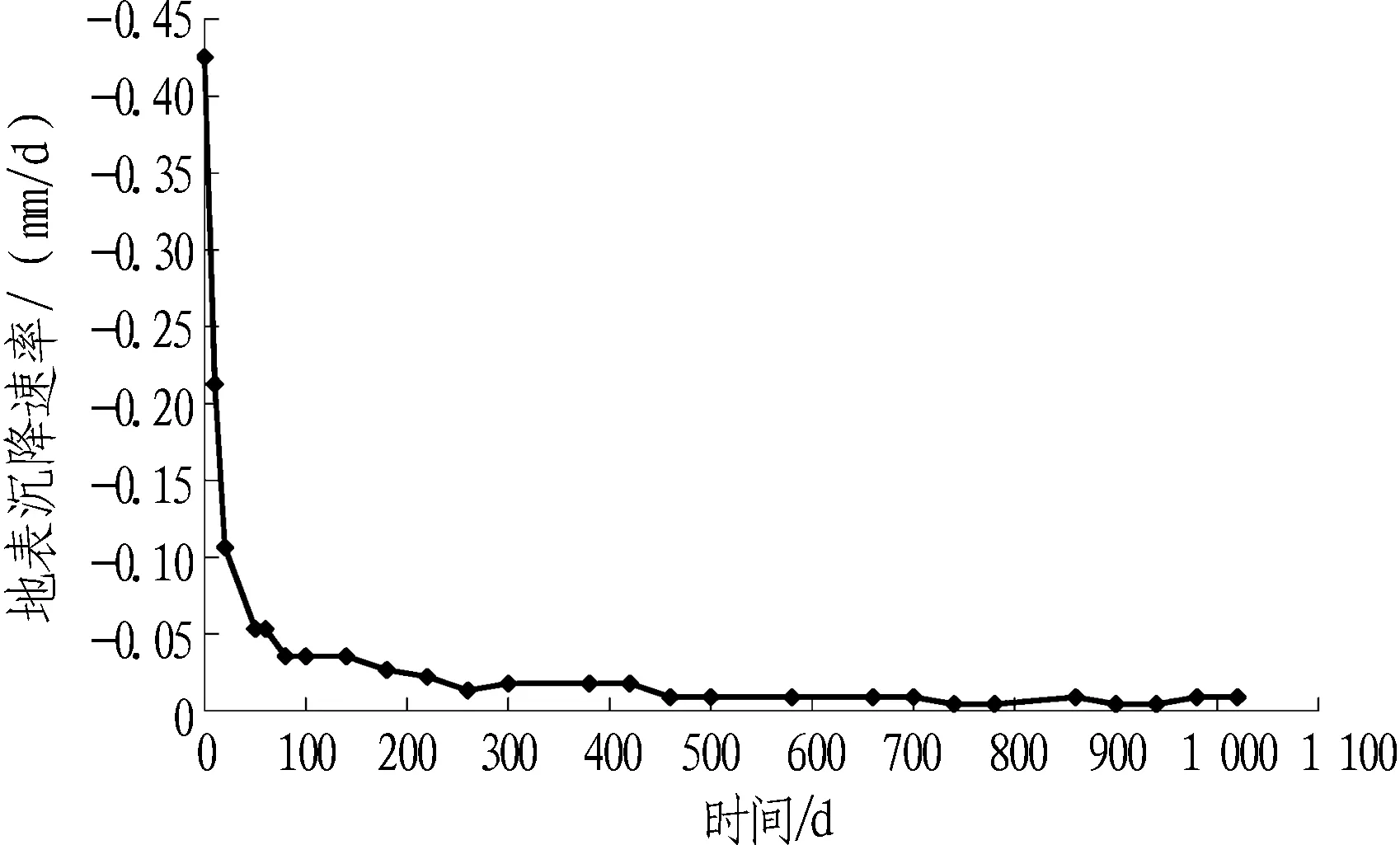
图11 隧道轴线上方地表计算日沉降速率曲线

Fig. 11 Curve of calculated daily ground surface settlement velocity above tunnel axial line

璩继立[21]的研究结果表明，虽然盾构施工引起的地面沉降槽宽度会随时间增长逐渐增大，但仍符合Peck提出的Gauss曲线分布规律。图12为本文方法计算得到的地表最终固结沉降计算值与Peck公式预测值比较。由图12可知，二者变化规律较为吻合，表明矩形顶管的地表固结沉降也大致符合Gauss曲线分布规律。

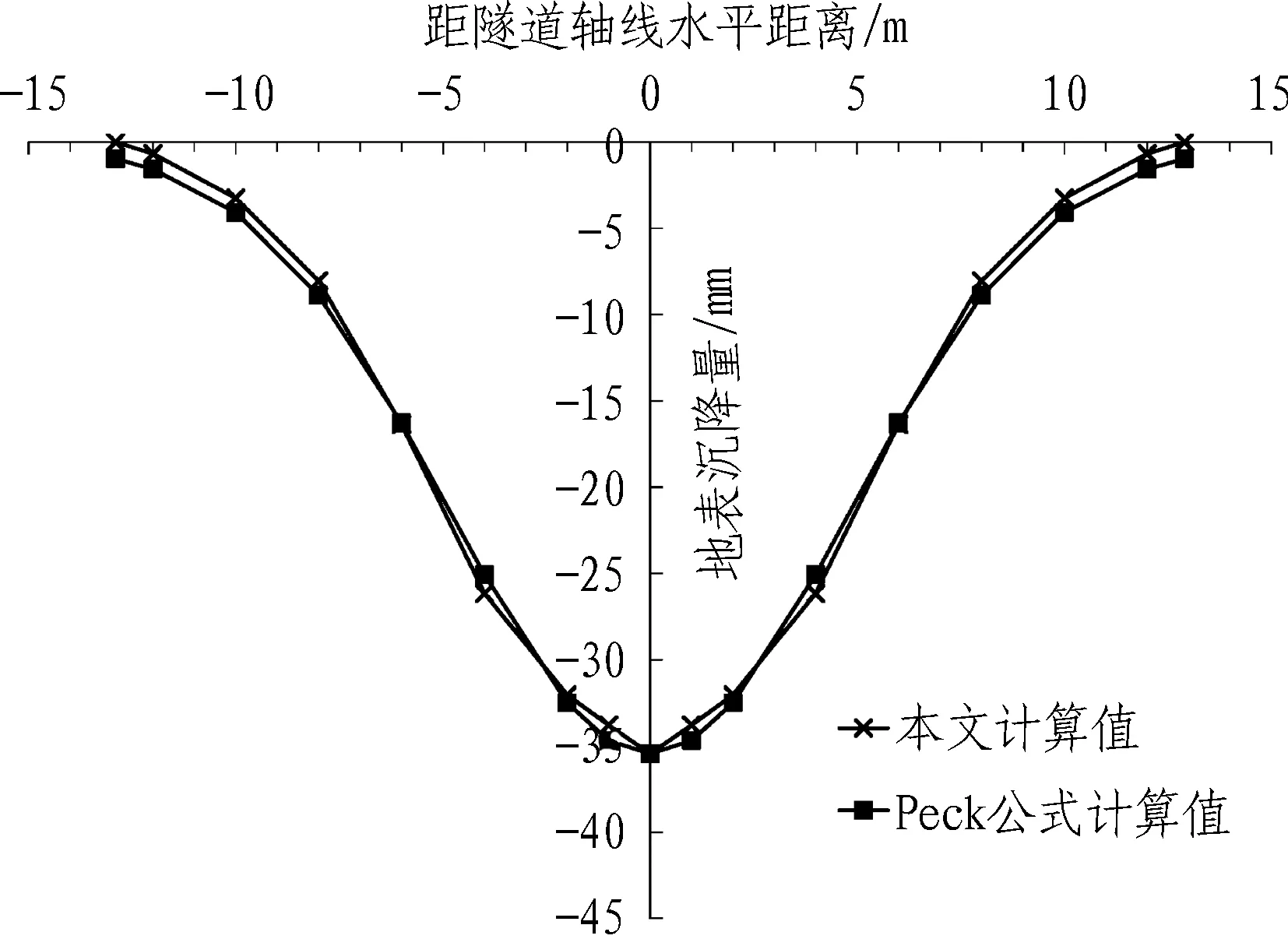
图12 地表最终固结沉降计算值与Peck公式预测值比较

Fig. 12 Comparison between final ground surface calculated settlements and predicted results by Peck formula

根据式(18)计算得到施工期间地表最大沉降量S1=20 mm，根据式(19)计算得到施工结束后地表最终最大固结沉降量S2=35.45 mm，二者叠加得到工后总的最终最大地表沉降量S=55.45 mm。工后固结沉降占总沉降的63.9%，不容忽视。但目前国内工程界对工后沉降还不够重视，仅在施工期间进行地表沉降监测，工后沉降几乎不考虑。本工程案例也是在顶管全部贯通后即停止实测，实测最大沉降量为27.57 mm，根据本文计算该断面后续还会产生27.88 mm的沉降量，这显然是不能忽略的。因此，建议在施工前先对工后沉降进行预测，根据计算结果来制定施工方案，同时延长监测时间，对工后监测频率可以适当降低。

4 结论与讨论

1)提出矩形顶管隧道施工引起的周围土体初始超孔隙水压力计算方法，进而得到土体初始超孔隙水压力等值线图。运用分层总和法计算地表固结沉降量，叠加施工阶段的地表沉降量，得到工后地表总沉降量的计算方法，进而预估最终沉降量。

2)本文方法计算得到的工后横向地表固结沉降计算值，其变化规律与Peck公式预测值较为吻合；横向地表总沉降值随着时间增长而逐渐增大，曲线基本符合正态分布规律。

3)工后地表沉降主要发生在施工结束后半年内，沉降速率在施工结束后的3个月内最大，随后半年内沉降速率的变化曲率迅速减小，并在较长时间沉降速率保持稳定。计算工后固结沉降占总沉降的60%以上，不容忽视。

本文研究中作了较多假定，仅考虑土体开挖应力释放引起的超孔隙水压力，没有考虑其他因素；土体扰动范围和超孔隙水压力的分布需作更深入的研究。另外需收集更多地表沉降实测数据，尤其是工后沉降数据，来进一步验证本文方法的可靠性。

[1] 林强强. 矩形顶管引起地面变形的实测分析与控制研究[D]. 上海： 同济大学, 2008.(LIN Qiangqiang. Research on experimental analysis and control of ground deformation induced by rectangular pipe jacking construction [D]. Shanghai: Tongji University, 2008.(in Chinese))

[2] 王日东. 矩形顶管施工引起的土体变形计算方法研究[J]. 佳木斯大学学报(自然科学版), 2014, 32(5): 711-714, 722.(WANG Ridong. Calculation methods of soil deformation induced by rectangular pipe jacking construction [J]. Journal of Jiamusi University (Natural Science Edition), 2014, 32(5): 711-714, 722. (in Chinese))

[3] 陈聪, 郑新定, 陈扬勋, 等. 武汉首例矩形顶管地铁出入口施工监测及数值模拟分析[J]. 隧道建设, 2013, 33(5): 354-361.(CHEN Cong, ZHENG Xinding, CHEN Yangxun, et al.Construction monitoring and numerical simulation analysis of the first Metro entrance/exit tunnel constructed by rectangular pipe jacking method in Wuhan[J]. Tunnel Construction, 2013, 33(5): 354-361. (in Chinese))

[4] 李铮华. 矩形顶管施工对邻近建筑物的影响分析[D]. 广州: 广州大学, 2014.(LI Zhenghua. Influence analysis of rectangular pipe jacking construction on adjacent buildings [D].Guangzhou: Guangzhou University, 2014. (in Chinese))

[5] 庞臣军, 鲍先凯. 矩形顶管施工的数值模拟研究[J]. 施工技术, 2012, 42(增刊): 410-412.(PANG Chenjun, BAO Xiankai. Study of numerical simulation of the rectangular pipe jacking construction [J]. Construction Technology, 2012, 42(S): 410-412. (in Chinese))

[6] 林晓庆. 过街通道矩形顶管施工土体变形分析[J]. 广州建筑, 2013, 41(1): 16-20.(LIN Xiaoqing. Analysis of soil deformation during rectangular pipe jacking construction of channel across the street [J]. Guangzhou Architecture, 2013, 41(1): 16-20. (in Chinese))

[7] 唐凯. 优秀历史建筑周边顶管施工的模拟分析与相应措施[J]. 住宅科技, 2013(3): 44-48.(TANG Kai. Simulation analysis of pipe-jacking construction around excellent historical building and corresponding measures [J]. Housing Science, 2013(3): 44-48.(in Chinese))

[8] 温锁林. 大断面矩形顶管施工对环境影响研究[J]. 中国市政工程, 2011(5)： 37-39.(WEN Suolin. Study of influence of large cross-section rectangular pipe jacking construction on environment[J]. China Municipal Engineering, 2011(5): 37-39. (in Chinese))

[9] 施文捷, 张志勇. 矩形顶管施工周边地质环境变化规律分析[J]. 上海地质, 2010, 31(3): 53-57.(SHI Wenjie, ZHANG Zhiyong. Analysis of changes law on geological environment for rectangular pipe jacking [J]. Shanghai Geology, 2010, 31(3): 53-57. (in Chinese))

[10] 郭亮. 大断面矩形顶管施工中的土体沉降规律分析[J]. 建筑施工, 2014, 36(6): 731-732.(GUO Liang. Analysis of regular settlement of surrounding soil mass during large cross-section rectangular pipe-jacking construction [J]. Building Construction, 2014, 36(6): 731-732.(in Chinese))

[11] 邓长茂, 彭基敏, 沈国红. 软土地区矩形顶管施工地表变形控制措施探讨[J]. 地下空间与工程学报, 2016, 12(4): 1002-1007.(DENG Changmao, PENG Jimin, SHEN Guohong. Discussion on control methods of ground surface settlement caused by rectangular pipe jacking construction in soft soils [J]. Chinese Journal of Underground Space and Engineering, 2016, 12(4): 1002-1007. (in Chinese))

[12] 熊翦. 矩形顶管关键受力分析[D]. 北京: 中国地质大学, 2013.(XIONG Jian. Analysis of key stress of rectangular pipe-jacking [D]. Beijing: China University of Geosciences, 2013. (in Chinese))

[13] 敖日汗, 张义同. 盾构施工引起的固结沉降分析[J]. 岩土力学, 2011, 32(7): 2157-2161.(AO Rihan, ZHANG Yitong. Analysis of consolidation settlements caused by shield tunneling [J]. Rock and Soil Mechanics, 2011, 32(7): 2157-2161. (in Chinese))

[14] 魏纲, 魏新江, 龚慈, 等. 软土中盾构法隧道引起的土体移动计算研究[J]. 岩土力学, 2006, 27(6): 995-999.(WEI Gang, WEI Xinjiang, GONG Ci, et al. Study of calculation for shield tunneling-induced ground movements in clays[J]. Rock and Soil Mechanics, 2006, 27(6): 995-999. (in Chinese))

[15] 魏新江, 陈伟军, 魏纲. 盾构施工引起土体超孔隙水压力峰值的计算及影响因素分析[J]. 岩土工程学报, 2012, 34(2)： 280-285.(WEI Xinjiang, CHEN Weijun, WEI Gang. Calculation and factors for distribution of initial distribution of peak value of excess pore water pressure due to shield construction [J]. Chinese Journal of Geotechnical Engineering, 2012, 34(2): 280-285. (in Chinese))

[16] 周顺华, 廖全燕, 刘建国, 等. 矩形顶管隧道顶进过程的地层损失[J]. 岩石力学与工程学报, 2001, 20(3)： 342-345.(ZHOU Shunhua, LIAO Quanyan, LIU Jianguo, et al. Stratum loss during pipe jacking of rectangle tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(3): 342-345. (in Chinese))

[17] 魏纲, 周洋, 魏新江. 盾构隧道施工引起的工后地面沉降研究[J]. 岩石力学与工程学报, 2013, 32(增刊1)：2891-2896.(WEI Gang, ZHOU Yang, WEI Xinjiang. Research on post-construction surface settlement caused by shield tunneling [J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(S1)： 2891-2896. (in Chinese))

[18] Peck R B. Deep excavations and tunneling in soft ground[C]//Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering. Mexico: [s.n], 1969.

[19] 华南理工大学, 东南大学，浙江大学，等. 地基及基础[M]. 北京: 中国建筑工业出版, 1991.(South China University of Technology, Southeast University, Zhejiang University, et al. Ground and foundation [M]. Beijing: China Architecture & Building Press, 1991. (in Chinese))

[20] 魏纲. 盾构法隧道地面沉降槽宽度系数取值的研究[J]. 工业建筑, 2009, 39(12): 74-79, 109.(WEI Gang. Study of calculation for width parameter of surface settlement trough induced by shield tunnel [J]. Industrial Construction, 2009, 39(12): 74-79, 109. (in Chinese))

[21] 璩继立. 盾构施工引起地面长期沉降研究[D]. 上海：同济大学， 2002.(QU Jili. Study of long-term ground surface settlement induced by shield tunneling[D]. Shanghai： Tongji University， 2002.(in Chinese))

Study of Calculation Methods for Ground Surface Settlement Induced by Rectangular Pipe Jacking Tunnel Boring in Soft Soil

WEI Gang, LI Zhiyuan, WANG Bin

(Department of Civil Engineering, Zhejiang University City College, Hangzhou 310015, Zhejiang, China)

The excess pore water pressure and ground surface settlement would be induced by rectangular pipe jacking tunnel construction. In this paper, the ground surface settlement induced by rectangular pipe jacking during construction phase is calculated by Peck formula. The calculation formula for excess pore water pressure of surrounding rocks is derived by stress releasing theory and stress transmission theory. The post-construction ground surface settlement induced by dissipation of initial excess pore water pressure is calculated by layerwise summation method. The calculation method for total ground surface settlement after consolidation is proposed; and the relationship between ground surface settlement and time and that between ground surface settlement velocity and time are studied. The calculation results in case study show that: 1) The ground surface settlement velocity reaches peak after 3 months of construction, and then decreases rapidly. 2) The curves of horizontal ground surface settlement and total ground surface show normal distribution.

rectangular pipe jacking; initial excess pore water pressure; post-construction ground surface settlement; soft soil stratum

2016-09-19；

2016-12-01

浙江省科技厅公益技术研究项目(2016C33051)； 住房和城乡建设部2015年科学技术项目计划(2015-K5-026)

魏纲(1977—)，男，浙江杭州人，2006年毕业于浙江大学，岩土工程专业，博士，教授，现从事地下隧道施工对周边环境影响及风险评估与控制研究工作。E-mail: weig@zucc.edu.cn。

10.3973/j.issn.1672-741X.2016.12.003

U 45

A

1672-741X(2016)12-1421-07