带精英保留策略的纵横交叉算法分布式电源规划

魏明磊，孟安波，黄海涛

(广东工业大学 自动化学院，广东 广州 510006)

带精英保留策略的纵横交叉算法分布式电源规划

魏明磊，孟安波，黄海涛

(广东工业大学 自动化学院，广东 广州 510006)

考虑分布式电源投资经济效益的基础上，建立以网络损耗费用、分布式电源发电售电收入、分布式电源投资与运行维护成本为目标的分布式电源规划模型，采用双向搜索机制的纵横交叉算法具有很强的全局收敛能力，但算法的竞争算子使粒子局限于“嫡系”粒子间的竞争，为保证粒子公平竞争,通过引入精英保留策略对纵横交叉算法进行改进，将改进的算法与IEEE 69节点系统相结合进行仿真实验，所得结果表明改进算法优化结果准确、合理，算法的全局搜索能力强，收敛精度高。

分布式电源规划; 网络损耗; 精英保留策略; 纵横交叉算法; 收敛精度

随着社会发展，传统能源面临着日益枯竭的困境，世界各国对分布式电源(distributed generation, DG)接入电网问题也日益重视[1-3]。配电网中大量接入DG会改变系统潮流大小和方向，使系统损耗不仅取决于负荷大小，还与分布式电源接入位置和容量关系密切[4-5]。分布式电源合理规划对电力系统的稳定运行具有重要意义[6]。

目前，国内外学者对分布式电源规划做了较多的研究。文献[7]建立了包含分布式电源接入配电网有功损耗目标函数，引入电压水平约束，将其转化为惩罚因子并入目标函数，得到有功损耗最优的分布式电源规划接入方案。文献[8]通过引入节点灵敏度系数矩阵和单位负荷增量成本矩阵，提出能够计及无功影响的配电网节点/支路边际容量成本模型及计算方法，分析DG并网对网络容量紧张程度的影响。文献[9]提出了考虑配电网结构变化的DG规划，采用损耗灵敏度因子对DG最优布置，建立以减少网损为目标的网络重构和DG容量配置的综合优化模型，对其进行仿真求解，得出有益结论，但模型仅考虑网络损耗，缺乏对规划成本的考虑。文献[10]对负荷和分布式电源的典型时序特性进行分析，建立了以网络损耗、停电损失为目标的考虑时序特性和多场景的多目标分布式电源规划，较真实反应配电网的各项经济技术指标。文献[11]以分布式电源售电费用与运行维护费用为规划模型,采用人工蜂群算法进行模型求解,验证建立模型的有效性以及所采用算法的收敛性。

本文以分布式电源接入电网所带来经济效益为目标[12]，通过优化分布式电源安装位置和容量，最大化安装分布式电源带来的收益，对纵横交叉算法进行改进，提出了带精英保留策略的纵横交叉算法分布式电源规划模型进行求解，验证算法的有效性和模型的可行性。

1 分布式电源规划模型

1.1 目标函数

本文首先建立含分布式点电源的配电网规划模型，在满足节点电压、电流、线路极限传输功率、功率频率等约束条件的同时，最大程度增加投入分布式电源所带来的经济效益，建立考虑售电收入、分布式电源投资和维护成本以及网络损耗费用的目标函数。

售电收入

(1)

式中：CDG为分布式电源发出的电能售卖给电网公司所赚取的收入；n为分布式电源接入数量，Tmax为年最大负荷利用时间；Cunit为单位电价；λi为i节点对应的分布式电源的容量系数，Pi,DG为i节点接入的分布式电源容量。

分布式电源投资和维护成本

(2)

式中：ε为固定年利率；m为布式电源规划年限；Ci,DG为i节点接入的分布式电源的安装成本；Ci,DG,main为i节点对应的分布式电源的运行维护成本。

网络损耗成本

(3)

式中：l为总支路数；Ri为支路电阻；PL为L支路的有功传输功率，QL为L支路的无功功率；UL为支路L的末端节点电压；TLmax为支路L的年最大负荷损耗时间。

考虑分布式电源售电收入、投资和运行维护成本和网络损耗成本，则归一化后的目标函数

(4)

1.2 约束条件

1.2.1 节点功率平衡约束

节点功率平衡约束条件为

式中：Pi、Qi为节点i中注入的有功功率和无功功率；N为系统节点数；ei和fi分别为i节点的节点电压实部和虚部；Gij、Bij分别为节点i、j之间之路的电导、电纳。

1.2.2 节点电压约束

节点电压约束条件为

(6)

式中：Uimin、Uimax分别为i节点最下允许电压和最大允许电压。

1.2.3 线路电流约束

节点电流约束条件为

(7)

式中：IL、ILmax分别为支路L的传输电流和最大允许传输电流。

1.2.4 线路传输功率约束

线路传输功率约束条件为

(8)

式中的PLmax为支路L的传输功率和极限传输功率。

1.2.5 分布式电源安装节点约束

分布式电源安装节点约束条件

(9)

式中：Xi为i节点分布式电源接入状态，当i=0时，表示i节点不接分布式电源；当i=1时，表示接分布式电源，D为最大安装节点数。

1.2.6 分布式电源安装容量约束

分布式电源安装容量约束条件

(10)

式中的PDG，max为系统分布式电源的最大安装容量。

2 带精英保留策略的纵横交叉算法

2.1 原始纵横交叉算法

纵横交叉算法(crisscross optimal algorithm, CSO)是由中国学者孟安波提出的一种全新的群智能优化算法[13-14]，它采用一种双向搜索机制—横向交叉和纵向交叉。横向交叉将粒子种群拆分成1/2大小的超立方体空间，每对配对父代粒子只在各自的超立方体子空间及其外缘繁殖后代；纵向交叉通过在种群纵向维度之间进行概率性交叉；将两种搜索机制交叉后形成的折中解通过竞争算子竞争淘汰产生最优解。

2.1.1 横向交叉方程式

(11)

式中：C1、C2为[1,1]上的随机数；r1、r2为[1,1]上的随机数；X(i,d)、X(j,d)分别是父代粒子X(i)、X(j)的第d维变量；Mhc(i,d)、Mhc(j,d)分别是X(i,d)、X(j,d)经横向交叉产生的第d维子代。横向交叉得到的子代粒子通过竞争算子与父代粒子进行比较，将适应度更高的粒子保存下来，并进入下一次迭代过程。

从式(11)可以看出，横向交叉以较大概率在以父代粒子X(i) 和X(j)为对角顶点的超立方体内繁殖后代MShc(i)和MShc(j)，同时又以较小概率在超立方体边缘外围搜索，概率分布如图1所示。通过这种跨界搜索机制，能够大大提高全局搜索能力。

图1 横向交叉概率分布

2.1.2 纵向交叉

纵向交叉是在种群个体粒子内部不同维度之间进行信息交叉的搜索机制，假设X(i,d1)、X(i,d2)分别表示父代个体粒子X(i)的第d1、d2维目标的信息。则交叉公式

(12)

式中：r∈U(0,1)；MSvc(i,d1)是个体粒子 X(i) 的第d1维和第d2维通过纵向交叉产生的第d1维后代。

由于纵向交叉在粒子不同维之间进行交叉，因此在交叉前需要对粒子的各维进行归一化操作。纵向交叉能够使“早熟”粒子跳出局部最优，保证种群的多样性。与横向交叉一样，纵向交叉结束后的子代粒子通过竞争算子将适应度高的粒子保存下来，进入下一次迭代。

2.2 改进纵横交叉算法

传统纵横交叉算法采用的竞争算子更新产生的子代种群虽然整体上适应度优于对应的父代种群，但是由于竞争过程中子代粒子和父代粒子是一对一的竞争关系，缺少对父代种群中其他粒子进行竞争比较，这样导致容易遗漏父代种群中的优秀粒子。为此本文在横向交叉、纵向交叉的基础上引入精英保留策略[15-16]，即用新的竞争策略代替原始的竞争算子。

精英保留策略是将父代种群中所有粒子、横向交叉产生的所有子代粒子以及纵向交叉产生所有子代粒子结合起来，形成种群规模大小为3×N的混合种群,将混合种群按照适应度大小顺序进行排列，并选择适应度高的前N个粒子作为最后的子代粒子Xs进入下一次迭代。引入精英保留策略的纵横交叉算法能为父代种群和子代种群提供群体竞争平台，保证所有子代种群中的粒子都为历史最优解，大大提高种群质量。

3 基于改进纵横交叉算法的DG规划

3.1 混合编码

结合改进纵横交叉算法的分布式电源规划，对分布式电源接入位置和容量进行混合整数编码。本文考虑了微型燃气轮和风力发电2种分布式电源，将风力发电设为集中接入，微型燃气机接入位置在系统中也已设定，因此在这里只需要进行容量优化。

首先对风电接入位置和容量进行编码，a1为风电接入位置，a2为接入容量；编码方式

再对微型燃气轮进行编码，令Pi,DG为i节点分布式电源安装容量，Pi,DG=XiPunit，其中，Punit为分布式电源的单位安装容量，Xi为分布式电源接入状态，当Xi=0时，表示i节点不安装微型燃气机，否则，i节点安装；因此得到微型燃气编码方式

将风电机组和微型燃气机的编码结合得到总的编码

3.2 改进纵横交叉算法的DG规划步骤

a) 设置种群大小N、分布式电源接入数目n和最大接入容量M、最大迭代次数Ψgen,max、横向和纵向交叉率Phc、Pvc等。

b) 初始化，对每个粒子进行混合编码形成初始种群，并将初始种群作为初始父代种群。

c) 将初始种群粒子带入到算例中利用前推回代法进行潮流计算，计算粒子的适应度和目标值；考虑到分布式接入电源的容量约束、节点电压约束，将其作为罚函数加入到目标函数中作为粒子适应度函数。

d) 将父代种群粒子分别带入横向交叉公式中，产生子代粒子Xhc，将子代粒子Xhc带入到算例中进行潮流计算，并计算粒子的适应度和目标值。

e) 将父代粒子进行归一化处理，将归一化后的粒子带入到纵向交叉公式中更新粒子，再反归一化，产生子代粒子Xvc，将子代粒子Xhc带入到算例中进行潮流计算，并计算粒子的适应度和目标值。

f) 将父代种群、横向交叉产生的子代粒子种群、纵向交叉产生的子代粒子种群结合起来，形成种群规模为3×N大小的混合种群；将混合种群中粒子按照适应度大小一次排序，选择适应度好的前N个粒子作为新的父代种群。

g) 判断是否满足终止条件。否，返回步骤d)继续迭代；是，输出最优子代粒子和对应的目标值、适应度，结束。算法流程如图2所示。

图2 算法流程

4 算例分析

本文选取IEEE 69[17]节点系统作为算例进行分布式电源规划，该系统含有68条支路，总有功负荷3 802 kW，总无功负荷2 694.6 kVA，在没有接入分布式电源时，系统的有功损耗为225 kW。将分布式电源作为P-Q节点接入，基准功率为100 MW，基准电压为12.66 kV，配电网结构如图3所示。分布式电源成本参数见表1。算法参数见表2。

注：数字带#的节点为微型燃气轮机接入位置，单机额定功率为100 kW，设定分布式电源最大安装台数为30台；数字带*的节点为风力发电机可选接入位置，风机的单机额定功率为600 kW，单个节点最大接入风机数为10台。图3 IEEE 69节点系统

表1 分布式电源成本参数

电源类型投资费用/(元·kW-1)运行维护费用/(元·kWh-1)容量系数风力发电机800000616050微型燃气轮机450002283100

表2 算法参数

种群规模M最大迭代次数权重系数ω加速因子C1、C2横向交叉率Phc纵向交叉率Pvc1001000402，210060

4.1 仿真结果

为验证该模型的可行性，本文利用改进纵横交叉算法对本文建立的模型进行仿真；同时为检验本文提出的改进纵横交叉算法的有效性和先进性，分别采用粒子群算法、传统的纵横交叉算法对算例进行仿真，并将本文算法优化结果与粒子优化算法(particle swarm optimization, PSO)、CSO的优化结果进行比较。其中，算法参数设置如表2，最大负荷利用时间Tmax=4 600 h，单位电价取0.50元/kWh。

3种算法在IEEE 69算例中的仿真结果见表3、表4，其中，表3为算法优化后的最优目标，表4为最优配置方案。

表3 最优方案费用 万元

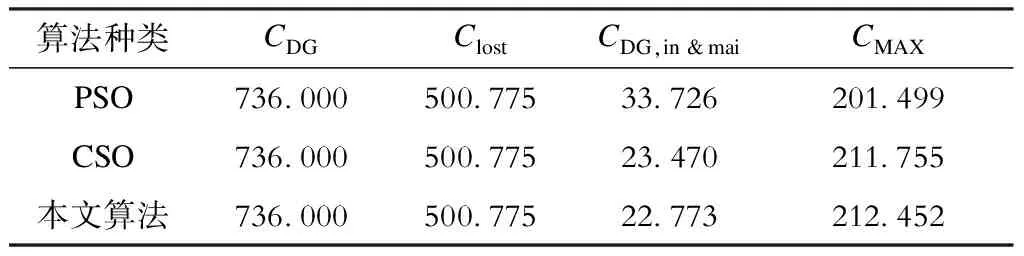
算法种类CDGClostCDG，in&maiCMAXPSO73600050077533726201499CSO73600050077523470211755本文算法73600050077522773212452

由表3可以看出：PSO收敛的总收益是3种算法中最低的，CSO算法次之，本文改进算法的优化

表4 最优分布式电源安装方案

总收益最高, 其中，3种算法所求得的售电费用和分布式电源投资运行维护费用一样，与之相对应，在表4中，3种方案安装的分布式电源种类及对应数量完全一样，由式(4)的目标函数可知，此时3种算法总收益大小取决于各分布式电源配置方案对系统网损的影响，由上分析可以看出本文改进的纵横交叉算法网损费用优化最好。

4.2 算法性能

对3种算法的性能进行分析，得到3种算法的收敛曲线如图4所示。

图4 收敛曲线

由图4的各种收敛曲线可以看出，PSO算法的收敛速度最快，CSO算法收敛速度最慢，而本文改进的算法较传统的CSO算法得到了明显的改善，这是由于PSO算法缺乏适当的引导机制导致种群很快陷入局部最优无法跳出，导致收敛精度最差；而CSO算法通过横向、纵向双向搜索机制，具有很强的全局搜索能力，但由于竞争算子竞争后的占优解容易遗漏了父代种群中优秀的粒子，导致收敛精度降低。本文提出的改进纵横交叉算法将竞争算子改为更高效的精英保留策略，保留CSO很强的全局搜索能力的同时，加入精英保留策略，提高了算法的收敛精度，3种算法对比，本文提出的算法收敛精度最高。在收敛到最优解的计算时间上，PSO、CSO以及本文算法的计算时间都较短，分别为137 s、166 s、150 s，粒子群算法由于粒子群算法很快陷入局部最优，收敛时间最快，本文算法由于采用精英保留策略、提高了种群粒子质量，相比传统纵横交叉算法收敛时间大大的减少。

5 结束语

本文建立了考虑分布式电源售电费用、分布式电源投资维护费用以及网损费用的配电网分布式电源规划模型，在CSO算法横向、纵向交叉的基础上引入精英保留策略思想改进纵横交叉算法，将改进的算法结合在IEEE 69节点的配电网系统进行仿真实验。实验结果表明，本文算法收敛效果好，收敛精度高，收敛速度较传统CSO得到进一步提高，所建立的模型对分布式电源规划问题具有一定参考意义。但是，模型中将风机和微型燃气机的出力作为恒定值出力，未考虑出力随机性，存在一定的不足，有待进一步深入研究。

[1] 马艺玮，杨苹，郭红霞，等.风-光-沼可再生能源分布式发电系统电源规划[J]. 电网技术, 2012,36(9): 9-14.

MA Yiwei, YANG Ping, GUO Hongxia， et al. Power Source Planning of Wind-PV-Biogas Renewable Energy Distributed Generation System[J]. Power System Technology，2012，36(9): 9-14.

[2] 黄付顺，王倩，何美华，等.基于综合敏感性分析的时序分布式电源规划[J]. 电力系统保护与控制, 2015(10): 44-50.

HUANG Fushun, WANG Qian, HE Meihua, et al. Timing Distributed Power Planning Based on a Comprehensive Sensitivity Analysis[J]. Power System Protection and Control，2015(10): 44-50.

[3] 陈海东，庄平，夏建矿，等.基于改进萤火虫算法的分布式电源优化配置[J]. 电力系统保护与控制， 2016(1): 149-154.

CHEN Haidong, ZHUANG Ping, XIA Jiankuang, et al. Optimal Power Flow of Distribution Network with Distributed Generation Based on Modified Firefly Algorithm[J]. Power System Protection and Control，2016(1): 149-154.

[4] 丁晓群，周春泉，杨保，等.基于多种群免疫算法的分布式电源选址与定容[J]. 电测与仪表，2014(4): 29-34.

DING Xiaoqun， ZHOU Chunquan， YANG Bao, et al. Sitting and Sizing of Distribution Generation Basedon Multi-population Immune Algorithm[J]. Electrical Measurement & Instrumentation，2014(4): 29-34.

[5] 刘煌煌，雷金勇，蔡润庆，等.基于SVM-MOPSO混合智能算法的配电网分布式电源规划[J]. 电力系统保护与控制，2014(10): 46-54.

LIU Huanghuang，LEI Jinyong， CAI Runqing，et al. Distributed Generation Planning in Distribution Network Based on Hybrid Intelligent Algorithm by SVM-MOPSO[J]. Power System Protection and Control，2014(10): 46-54.

[6] 陈海东.基于细菌菌落优化算法分布式电源优化配置[J]. 电力系统保护与控制，2015(21): 106-111.

CHEN Haidong.Optimal Power Flow of Distribution Network with Distributed Generation Based on Bacterial Colony Optimization[J]. Power System Protection and Control，2015(21): 106-111.

[7] 任龙霞，雷金勇，甘德强.计及配电网节点/支路边际容量成本的分布式电源规划[J]. 电力系统自动化，2010(21): 34-39.

REN Longxia, LEI Jinyong, GAN Deqiang.Distributed Generator Planning in Distribution Network Considering Locational/Branch Marginal Capacity Cost Mode[J]. Automation of Electric Power Systems，2010(21): 34-39.

[8] 高艺文，刘俊勇，雷成，等.考虑配电网结构变化的DG规划[J]. 电力系统保护与控制, 2014(4): 40-46.

GAO Yiwen，LIU Junyong，LEI Cheng，et al.DG Planning Considering the Variation of the Distribution Network Structure[J]. Power System Protection and Control，2014 (4): 40-46.[9] 李亮，唐巍，白牧可，等.考虑时序特性的多目标分布式电源选址定容规划[J]. 电力系统自动化，2013,37 (3): 58-63.

LI Liang, TANG Wei, BAI Muke, et al. Multi-objective Locating and Sizing of Distributed Generators Based on Time-sequence Characteristics[J]. Automation of Electric Power Systems，2013,37 (3): 58-63.

[10] 周文越，吕飞鹏，廖小君.基于人工蜂群算法的分布式电源规划[J]. 电力系统及其自动化学报，2014(5): 39-43.

ZHOU Wenyue，LÜ Feipeng， LIAO Xiaojun.Optimal Planning of Distributed Generation Based on Artificial Bee Colony Algorithm[J]. Proceedings of the CSU-EPSA，2014(5): 39-43.

[11] 殷豪, 周玉龙, 孟安波.二进制纵横交叉算法在配电网重构中的应用[J]. 电网技术, 2016,40(1):270-275

YIN Hao，ZHOU Yulong， MENG Anbo.Application of Binary Crisscross Optimization Algorithm to Distribution Network Reconfiguration[J]．Power System Technology，2016，40(1): 270-275.

[12] 张立梅，唐巍，王少林，等.综合考虑配电公司及独立发电商利益的分布式电源规划[J]. 电力系统自动化，2011, 35(4): 23-28.

ZHANG Limei, TANG Wei, WANG Shaolin, et al. Distributed Generators Planning Considering Benefits for Distribution Power Company and Independent Power Suppliers[J]. Automation of Electric Power Systems，2011，35(4): 23-28.

[13] 孟安波，卢海明，李海亮，等.纵横交叉算法优化FCM在电力客户分类中的应用[J]. 电力系统保护与控制, 2015, 43(20): 150-154.

MENG Anbo，LU Haiming， LI Hailiang, et al. Electricity Customer Classification Based on Optimized FCM Clustering by Hybrid CSO[J]. Power System Protection and Control, 2015,43(20): 150-154.

[14] 张璐，唐巍，丛鹏伟，等.含光伏发电的配电网有功无功资源综合优化配置[J]. 中国电机工程学报， 2014,34(31): 5525-5533.

ZHANG Lu, TANG Wei, CONG Pengwei, et al. Optimal Configuration of Active-reactive Power Sources in Distribution Network with Photovoltaic Generation[J]. Proceedings of the CSEE, 2014,34(31): 5525-5533.

[15] 杨树欣，詹宁波，田林怀.一种改进的量子遗传算法及其应用[J]. 计算机工程， 2013(5): 196-199.

YANG Shuxin, ZHAN Ningbo, TIAN Linhuai.An Improved Quantum Genetic Algorithm and Its Application[J]. Computer Engineering, 2013(5): 196-199.

[16] 唐林权，李芝荣，李如琦，等.基于最优引导策略的分布式电源优化配置[J]. 现代电力， 2014, 31(1): 23-27.

TANG Linquan, LI Zhirong, LI Ruqi, et al. Distributed Generation Planning Based on the Optimized Guidance Strategy[J]. Modern Electric Power, 2014, 31(1): 23-27.

[17] 韩天雄，熊家伟，赵宪，等.进化规划算法在分布式电源选址和定容中的应用[J]. 电力学报, 2013(5): 370-373.

HAN Tianxiong, XIONG Jiawei，ZHAO Xian，et al. Evolutionary Programming Method and Its Application in the Locating and Sizing of the Distributed Generator[J]. Journal of Electric Power，2013(5): 370-373.

(编辑 王夏慧)

Distributed Generation Planning Based on Crisscross Algorithm with Elite Strategy

WEI Minglei, MENG Anbo, HUANG Haitao

(School of Automation, Guangdong University of Technology, Guangzhou, Guangdong 510006, China)

On the basis of considering investment economic benefit of distributed generation (GD), a DG planning model taking network loss cost, income of DG generate electricity and electricity selling, DG investment and operation maintenance costs as targets. Crisscross algorithm adopting bidirectional research mechanism has very strong global convergence ability, but the competition operator of this algorithm will make particles limit to competition among direct descendant particles. In order to ensure fair competition, elite strategy was introduced to improve crisscross algorithm and simulation experiment was conducted by combining the improved algorithm and IEEE 69 node system. Results obtained indicate that the improved algorithm has more accurate and reasonable optimized result as well as strong global research ability and high convergence precision.

distributed generation planning; network loss; elite strategy; crisscross algorithm; convergence precision

2016-07-03

2016-09-20

广东省科技计划项目(2016A010104016)

10.3969/j.issn.1007-290X.2016.12.004

TM715

A

1007-290X(2016)12-0015-06

魏明磊(1991)，男，安徽滁州人。在读硕士研究生，主要研究方向为电力系统运行与控制。

孟安波(1971)，男，重庆人。副教授，工学博士, 研究生导师，主要研究方向为电力系统自动化，系统分析与集成。

黄海涛(1987)，男，广东汕尾人。在读硕士研究生，研究方向为电力系统无功优化。