基于Hankel矩阵联合近似对角化的结构模态识别*

程 琳， 杨 杰， 郑东健， 任 杰

(1. 西安理工大学西北旱区生态水利工程国家重点实验室培育基地 西安, 710048)(2. 河海大学水文水资源与水利工程科学国家重点实验室 南京, 210098)



基于Hankel矩阵联合近似对角化的结构模态识别*

程 琳1,2， 杨 杰1， 郑东健2， 任 杰1

(1. 西安理工大学西北旱区生态水利工程国家重点实验室培育基地 西安, 710048)(2. 河海大学水文水资源与水利工程科学国家重点实验室 南京, 210098)

针对基于二阶盲辨识(second order blind identification，简称SOBI)的模态参数识别方法存在的不足，提出了一种基于Hankel矩阵联合近似对角化(Hankel matrix joint approximate diagonalization，简称HJAD)技术的结构运行模态分析(operational modal analysis，简称OMA)的新方法。该方法通过对随机子空间类模态识别方法常用的Hankel矩阵进行联合近似对角化，以分离各阶模态响应，进行模态识别。与基于SOBI的模态识别方法相比，在具体实施过程中，仅需要在分析数据中添加与实测振动响应对应的时间延迟的数据，实现难度较小。数值算例和物理模型试验的分析结果表明，所提出的基于HJAD技术的结构运行模态分析方法，不仅具有鲁棒性强和计算效率高的优点，还可以克服传统的基于SOBI的模态识别方法的模态识别能力受测点数目限制的问题。

运行模态分析；盲源分离；二阶盲辨识；Hankel 矩阵联合近似对角化；振动台试验

引 言

根据实测振动数据来识别结构的模态参数并计算模态指标，再应用相关模态指标来评价结构的健康状态，是基于振动的结构健康诊断方法的基本思路[1]。为了研究大坝等大型工程结构的振动特性，需要对其施加一定的振动激励。传统的大型结构原型动力试验[2]需要施加人工产生的激励，如起振机和爆破等，不仅耗费巨大，可能对结构产生破坏，而且人工激励与结构正常运行时可能遇到的振动激励差异很大。因此，研究各种环境激励，包括地震、脉动风、脉动水压力和交通振动等作用下大型工程结构的模态识别方法显得十分必要。

环境激励下结构模态参数的识别方法，也被称为结构的运行模态分析[3-4]，一般仅根据结构的振动响应来识别模态参数。目前常用的运行模态分析方法主要包括频域类方法、时域类方法、时频分解算法和SOBI法等。在上述各种方法中：频域类方法的识别精度有待提高；时域类方法常常要用到矩阵分解技术，计算量很大；时频分解算法在计算中存在参数选择困难和边界效应等问题。模态识别的SOBI方法[5]由于其在模态参数识别方面表现出鲁棒性强和计算效率高等优点，受到了广泛的关注[6-7]。然而，基于SOBI的模态识别方法，只能识别出与测量自由度数相同的模态阶数，模态识别能力受到测点数目的限制，并且该方法在系统定阶方面也存在困难，限制了其在实际工程中的应用。

为了克服传统SOBI模态识别方法存在的模态识别能力受测点数目限制的问题，笔者提出了HJAD技术的结构运行模态分析方法，并将该方法与稳态图相结合，以解决系统定阶和剔除虚假模态的问题。通过一个数值算例和一个物理模型试验，验证了该方法在识别精度、鲁棒性和计算效率等方面的表现。

1 环境激励下基于SOBI的模态识别

1.1 自然激励技术

各种环境激励本身的性质复杂，实际应用中常常将其简化成随机的带限白噪声。随机环境激励下，结构的受迫振动响应也是随机的，而结构的模态参数识别一般是基于其自由振动响应或脉冲响应的。因此，需要研究从随机受迫振动响应中提取结构自由响应或脉冲响应的方法。

n自由度结构的振动平衡方程可以表达为

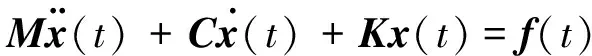
(1)

其中：M，K和C分别为系统的质量、刚度和阻尼矩阵；f(t)为外部激励；x(t)为位移响应。

环境激励一般不可直接测量，并且与噪声相比，二者的幅值常常没有显著的差异。因此，环境激励下结构的振动一般可以表达为以下的随机离散状态空间模型[8]

(2)

其中：zk为离散的系统状态变量；yk为系统观测量；A为离散系统矩阵；G为观测矩阵；wk为环境激励和系统误差；vk为观测噪声。

如果观测噪声也是随机白噪声，根据式(2)进行推导，可以得到各测点振动观测间的相关函数矩阵的表达式

(3)

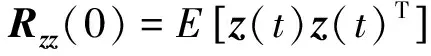
由式(3)可以看出，白噪声激励下结构各测点振动观测间的相关函数与结构的脉冲响应以及自由振动响应类似，仅与结构的初始状态和系统参数(模态参数)有关。因此，当环境激励和观测噪声接近白噪声时，可以采用结构各测点响应间的互相关函数代替脉冲响应或自由振动响应来进行模态识别，这就是自然激励技术(nature excitation technique，简称NExT)[9]。

1.2 基于SOBI的模态识别

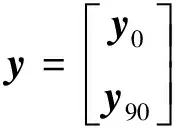
(4)

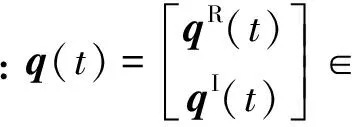
如果结构的各阶模态响应q(t)相互独立，结构的自由振动响应可以看作是各阶模态响应的线性混合，各阶模态响应被看作是虚拟源信号，混合矩阵即为L。这时可以采用盲源分离(blind source separation，简称BSS)方法来求解模态识别问题。在BSS的各种实现算法中，基于联合近似对角化(joint approximate diagonalization，简称JAD)技术的SOBI算法[11]在实际应用中表现出鲁棒性强和计算效率高等优点。下面基于该方法研究结构模态参数的识别问题。

假定观测噪声是高斯白噪声，这时可以得到各观测信号间的相关函数矩阵的表达式为

(5)

忽略阻尼影响，各阶模态响应相互独立，Rqq(τi)是一个对角阵。从式(4)可以看出，任意一个时延τi(i= 1, 2,…,S)，理论上应该存在矩阵P=L+使Ryy(τi)对角化，但实际的观测信号中总存在噪声，并且由于阻尼的存在，源信号也不能精确满足相互独立的条件。这时，对一组不同时延的矩阵进行JAD时，可以转而求解鲁棒性更强的优化问题min:Joff(U)，其中优化的目标函数为

(6)

其中：运算符号off(·) 表示提取矩阵所有非主对角元素；U为需要通过优化得到的对角化矩阵；W为白化矩阵。

白化的目的是使各混合通道的信号经过变换后相互独立，具有单位方差，以避免优化过程出现零解。一般采用主成分分析(principle component analysis,简称PCA)方法来确定白化矩阵W

(7)

其中：矩阵D为以Ryy(0)的特征值为对角元素的对角矩阵；F为其特征向量组成的矩阵。

用某一种数值方法对以上不同时延的协方差矩阵实施JAD，即求解式(6)的优化问题。常用的JAD实现技术包括雅克比方法、交替最小二乘法、并行因子分析、子空间拟合技术和旋转适量法等。这时，可以得到在JAD意义上的广义的正交矩阵U(而不是仅使某一个时滞协方差矩阵对角化)。这时，分离矩阵为

P=UHW

(8)

其中：H为共轭转置算子，对于实数而言即转置算子T。

源信号，即模态响应的估计为

(9)

混合矩阵为

(10)

其中：W+为W矩阵的广义逆矩阵。

式(5)是根据结构的自由响应来进行推导的，而实际工程中一般只能得到环境激励下结构的受迫振动响应。根据NExT可以采用环境激励下结构受迫振动响应间的相关函数矩阵来代替式(5)所示的结构自由振动间的相关函数矩阵，并进行JAD。分离得到的每一阶模态响应代表一个单自由度振动系统，可以采用单模态识别法(如最小二乘拟合法、时间序列法等)来识别对应的模态参数。模态振型可以从混合矩阵L中得到。

2 环境激励下基于HJAD的模态识别

对于实际工程结构而言，结构的模态阶数n是未知的，而且测点数目l常常远小于结构模态阶数n。一些分析结果表明，结构高阶模态参数对结构损伤更为敏感。因此，研究采用有限的振动测点，识别出尽可能多阶数的结构模态参数，具有十分重要的理论意义和应用价值。采用上述基于SOBI的模态参数识别方法时，最多只能识别与测点数目相同的l阶模态。模态识别能力受到测量自由度数l的约束，极大限制了SOBI在实际工程结构运行模态分析中的应用，因此需要研究改进的方法。

定义由实测振动响应及其时延数据形成的向量

(11)

其中：p为时间延迟。

p的设定原则是要使rank(H(τ)) ≥n成立。这时可以采用式(12)计算Hankel矩阵[12]

(12)

对于结构的自由振动，Rqq(τ)=ΣτRqq(0)成立。这时，根据式(5)对式(12)定义的Hankel矩阵进行推导可以得到

(13)

以上Hankel矩阵的分解形式与协方差矩阵的分解形式(5)是一致的。根据式(5)所示的分解形式，协方差函数矩阵可以采用JAD技术来进行联合近似对角化。对于Hankel矩阵，采用式(13)的分解形式，也同样可以对一组不同时延的Hankel矩阵，即H(τ1),H(τ2),…,H(τS)采用JAD技术实现近似对角化，并求解模态参数。对一组不同时延的Hankel矩阵进行联合近似对角化，可以转化成求解以下的优化问题min:Joff(U)，其中的优化目标函数Joff(U)为

(14)

3 数值验证

对图1所示的4自由度集中质量系统的模态参数进行识别。其参数如下：m1=m2=m3= 1 kg；m4= 0.9 kg；k1=k3= 7 kN/m；k2=k4= 8 kN/m；c1=c2= 0.6 (N·s2)/m；c3=c4= 0.55 (N·s2)/m，系统的初始状态设为零。基础环境激励ag(t)采用高斯白噪声来模拟。结构的振动观测物理量是绝对加速度，采用加速度响应的计算结果加上一定水平的噪声来模拟。结构振动响应的计算采用Runge-Kutta 算法来实现，模拟加速度观测的采样频率为100 Hz。结构自振频率的理论值为5.172，13.524，21.872 Hz和26.019 Hz；阻尼比的理论值分别为0.144%，0.346%，0.510%和0.620%。对于无噪声的观测数据，分别采用1，2，3和4个测点来识别结构的模态参数，识别结果见表1。传统的基于SOBI的模态识别方法仅能识别出与测点数目相同的模态阶数，而采用HJAD方法，即使在仅有1个测点的情况下，也可以识别出结构的各阶自振频率和阻尼比。根据1个测点(m4)的振动响应，采用基于HJAD技术的模态识别方法分离得到的结构前2阶模态响应及其功率谱如图2所示。

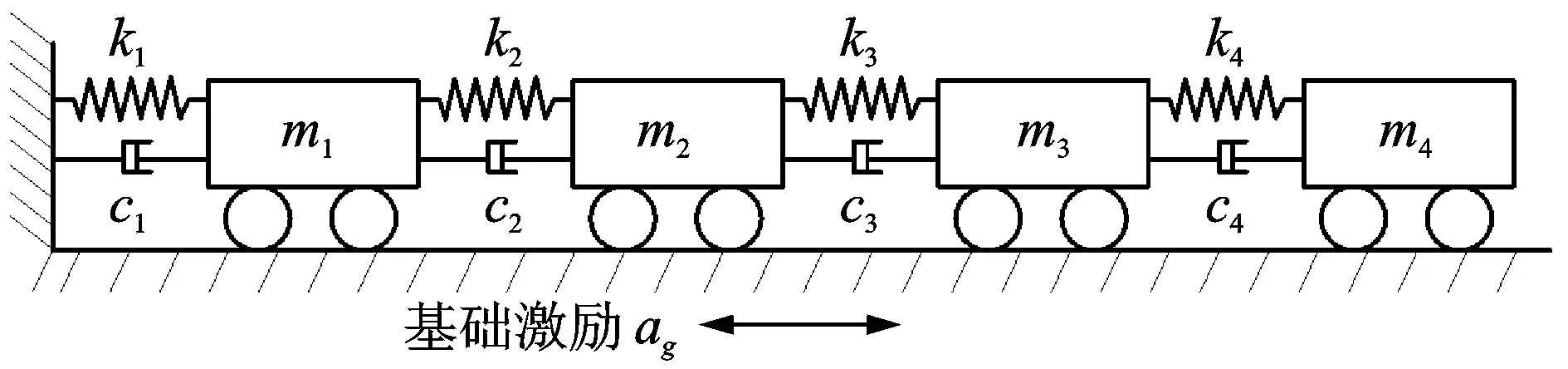
图1 4自由度集中质量系统Fig.1 Concentrated mass system of 4 degrees of freedoms

Tab.1 Identification results of nature frequencies and damping ratios

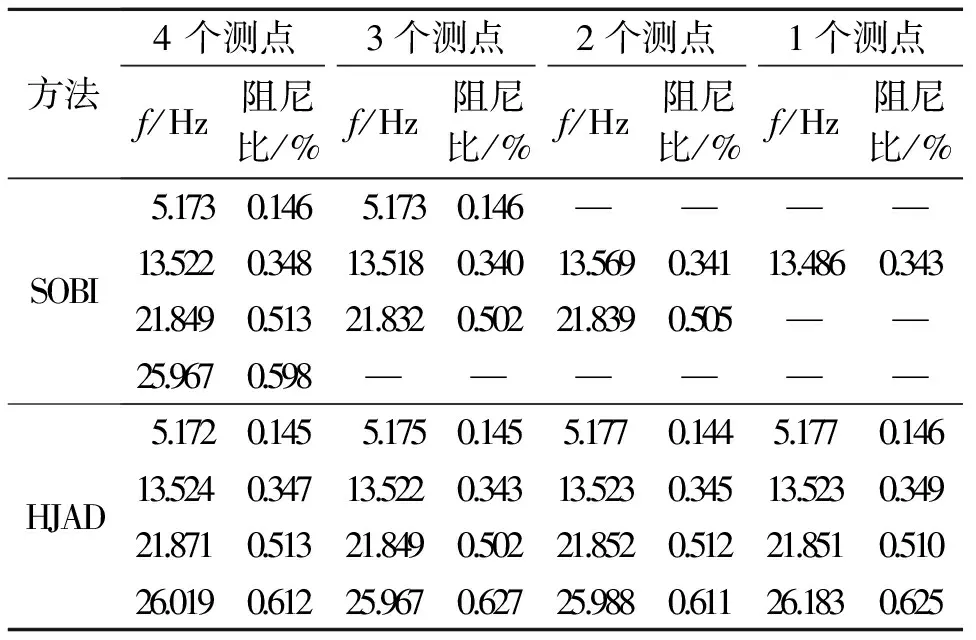
方法4个测点3个测点2个测点1个测点f/Hz阻尼比/%f/Hz阻尼比/%f/Hz阻尼比/%f/Hz阻尼比/%SOBI5．1730．1465．1730．146————13．5220．34813．5180．34013．5690．34113．4860．34321．8490．51321．8320．50221．8390．505——25．9670．598——————HJAD5．1720．1455．1750．1455．1770．1445．1770．14613．5240．34713．5220．34313．5230．34513．5230．34921．8710．51321．8490．50221．8520．51221．8510．51026．0190．61225．9670．62725．9880．61126．1830．625

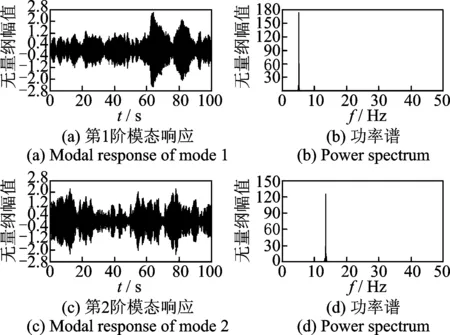
图2 模态响应及其功率谱Fig.2 Modal responses and power spectrums

采用测点2，3和4对应的振动响应数据进行结构振型的识别，根据振型的识别值和理论值计算的的模态置信因子(modal assurance criteria，简称MAC)见表2。

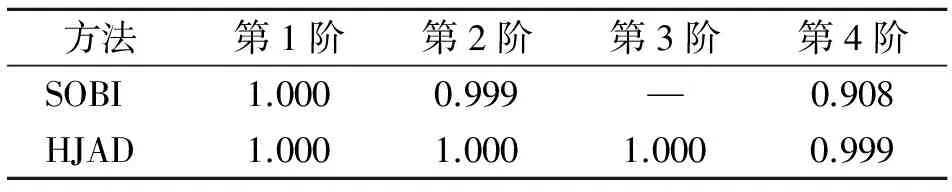
表2 振型的识别精度

所有振型都采用第4个测点的坐标值进行归一化。从表2可以看出，HJAD技术可以识别4阶振型，而SOBI算法仅能识别3阶振型。由于结构的损伤常常在高阶模态上表现更为显著，采用有限的测点，准确地识别结构尽可能多阶的模态参数，可以对结构的损伤诊断提供很大的便利。为了验证笔者提出的模态识别方法的鲁棒性，根据4个测点的振动响应在不同信噪比(signal noise ratio，简称SNR)水平下，采用特征系统实现算法(eigensystem realization algorithm，简称ERA)、随机子空间方法(stochastic subspace identification，简称SSI)和基于HJAD技术的方法进行模态参数识别，自振频率的识别误差随SNR的变化见图3。

图3 自振频率的识别结果对比Fig.3 Comparison of the identification results of nature frequencies

由图3可以看出，随着噪声水平的提高(SNR减小)，基于HJAD技术的模态识别方法的识别结果更稳定。在高噪声水平下，其模态参数的识别精度更高。

4 试验验证

根据某混凝土重力坝的一个挡水坝段，按照几何相似的原则(比例为1∶160)制作试验模型，并进行小型振动台试验。试验模型的材料采用混凝土砂浆，质量密度为2 100 kg/m3，水灰比为水∶细砂∶水泥 = 1∶2.9∶2.09。试验中环境激励通过振动台产生的带限白噪声来模拟，考虑到模型自振频率的范围和采样的要求，设定带限白噪声激励的频率范围为100～2 000 Hz，采样频率为4 kHz。模型共布置6个单向的压电式加速度传感器，如图4所示，传感器等间距布置，间距为10cm。采用DSPACE数据采集系统来测量模型的加速度响应，6个测点实测的加速度响应如图5所示。

图4 试验模型和试验布置Fig.4 The experimental model and the layout of the experiment

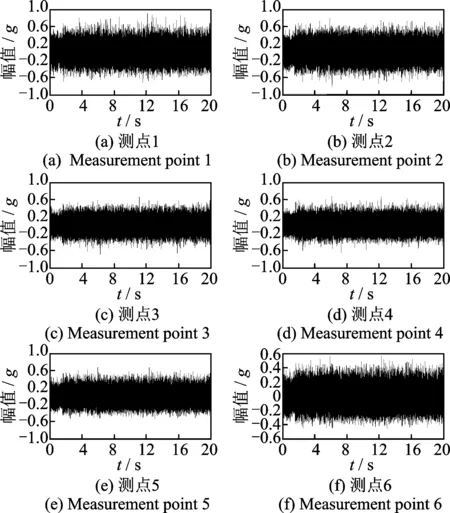
图5 模型的实测振动响应Fig.5 The measured vibration response of model

采用带通滤波器来滤除低频的趋势分量和无效的频率分量。频率的通带根据有限元计算的结果来确定，然后采用小波阀值去噪法进行去噪处理。根据处理后的振动响应分别采用SOBI方法、SSI方法和HJAD方法进行模态参数识别的结果，以及采用有限单元法(finite element method，简称FEM)计算的结果见表3。由表3可以看出，在前7阶模态中，SOBI方法仅能识别4阶模态，而SSI和HJAD法的识别结果相近，可以识别出6阶模态。各种方法都未识别出第4阶模态，可能是在环境激励下，该阶模态响应太微弱，无法识别。计算中，SSI识别方法的计算时间大约为HJAD方法的5倍。采用SSI方法、HJAD方法识别的振型与FEM计算结果的对比见图6。自振频率和振型识别结果与FEM计算结果有一定的误差，主要是由有限元模拟误差(材料和边界条件等方面)和计算识别误差等因素造成的。

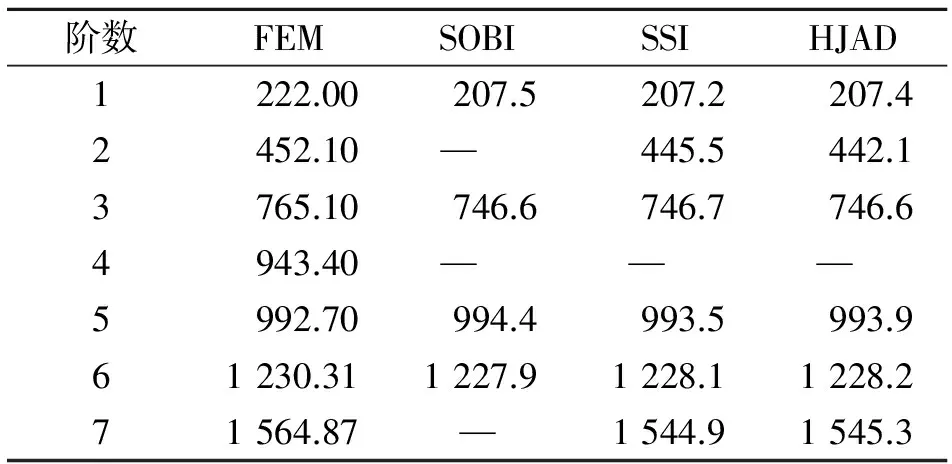
表3 自振频率的识别结果

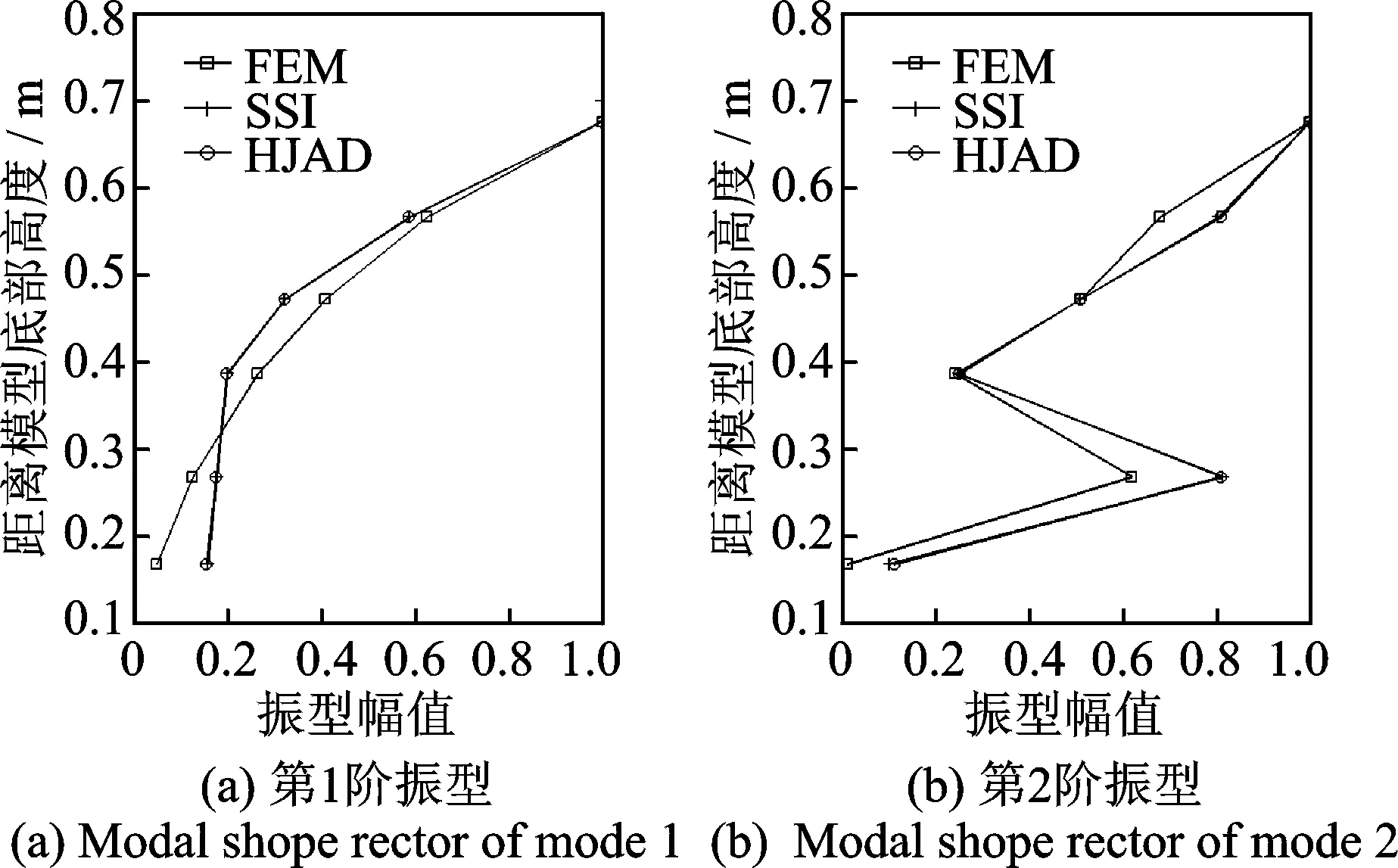
图6 前2阶振型识别结果的对比Fig.6 The comparison of the identification results of the first two modal shapes

5 结束语

基于HJAD技术的模态识别方法既可以看作是在时域模态参数识别方法中，引入计算效率高和鲁棒性强的JAD技术，也可看作是将SOBI算法中采用的各测点响应间的协方差函数矩阵，用Hankel矩阵来代替，以实现系统扩阶。实例分析表明，基于HJAD技术的结构模态参数识别方法鲁棒性强，模态识别结果更稳定，精度更高，克服了传统的基于SOBI的模态识别方法的模态识别能力受测点数目限制的问题，并且算法的计算效率也很高。这些优点为其在实际工程中的应用提供了良好的前景。

[1] Farrar C, Doebling S, Nix D. Vibration-based structural damage identification [J]. Philosophical Transactions of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences, 2001, b(359): 131-149.

[2] 张光斗, 张楚汉, 李未显, 等. 泉水拱坝的振动测量与分析[J]. 中国科学A辑, 1986, 1: 100-112.

Zhang Guangdou, Zhang Cuhan, Li Weixian, et al. Vibration measurement and analysis of Quanshui arch dam [J]. Science China, Series A, 1986, 1: 100-112.(in Chinese)

[3] 张建伟, 李火坤, 练继建, 等. 基于环境激励的厂房结构损伤诊断与安全评价[J]. 振动、测试与诊断, 2013, 33(4) : 670-674.

Zhang Jianwei，Li Huokun, Lian Jijian, et al. Damage diagnosis and safety evaluation of underground powerhouse under ambient excitation [J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(4): 670-674.(in Chinese)

[4] 续秀忠, 华宏星, 陈兆能. 基于环境激励的模态参数辨识方法综述[J]. 振动与冲击，2002, 21(3): 1-5.

Xu Xiuzhong, Hua Hongxing, Chen Zhaoneng. Review of modal identification method based on ambient excitation [J]. Journal of Vibration and Shock, 2002, 21(3): 1-5.(in Chinese)

[5] 曹军宏, 韦灼彬, 刘树勇. 改进型盲源分离在结构模态识别中的应用 [J]. 振动、测试与诊断, 2013, 33(4): 689-693.

Cao Junhong, Wei Zhuobin, Liu Shuyong. Application of improved blind source separation in modal parameter identification [J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(4): 689-693.(in Chinese)

[6] Antoni J, Brun S. Special issue on blind source separation: editorial[J]. Mechanical Systems and Signal Processing, 2005, 19:1163-1165.

[7] McNeill S. Modal identification using blind source separation techniques [D].Houston, Texas:University of Houston, 2007.

[8] Van Overschee P, De Moor B. Subspace identification for linear systems: theory, implementation, applications [M]. Dordrecht, the Netherlands: Kluwer Academic Publishers, 1996: 57-73.

[9] James G H, Carne T G, Lauffer J P. The natural excitation technique for modal parameter extraction from operating structures [J]. Modal Analysis: International Journal of Analytical and Experimental Modal Analysis, 1995, 10(4): 260-277.

[10]McNeill S I. An analytic formulation for blind modal identification [J]. Journal of Vibration and Control, 2012, 18(14): 1-11.

[11]Belouchrani A, Abed-Meraim K, Cardoso J F, et al. A blind source separation technique using second-order statistics [J]. IEEE Transactions on Signal Processing, 1997, 45 (2): 434-444.

[12]Antoni J, Chauhan S. A study and extension of second-order blind source separation to operational modal analysis [J]. Journal of Sound and Vibration, 2012, 18 (14): 2111-2121.

10.16450/j.cnki.issn.1004-6801.2016.06.018

*国家自然科学基金资助项目(51409205)；博士后自然科学基金资助项目(2015M572656XB)；陕西省重点科技创新团队资助项目(2013KCT-015)；水文水资源与水利工程科学国家重点实验室开放研究基金资助项目(2014491011)

2014-05-17；

2015-10-29

TV32；TU311

程琳，男，1986年7月生，讲师。主要研究方向为水工结构安全监控和无损检测。曾发表《Two online dam safety monitoring models based on the process of extracting environmental effect》(《Advances in Engineering Software》2013, Vol.57)等论文。 E-mail：wanmu2381@163.com