基于结构方程模型的数学建模翻转教学满意度路径研究*

叶聪相 王积建

(1.浙江工贸职业技术学院 信息传媒学院，浙江 温州 325027；2.浙江工贸职业技术学院 人文学院，浙江 温州 325027)



基于结构方程模型的数学建模翻转教学满意度路径研究*

叶聪相1王积建2

(1.浙江工贸职业技术学院 信息传媒学院，浙江 温州 325027；2.浙江工贸职业技术学院 人文学院，浙江 温州 325027)

为了提高数学建模教学质量，文章中建立了以世界大学城为平台的翻转教学模式，以连续5个学期的数学建模选修课为教学实验班。综合国内外量表，结合我国高校情况制定问卷，通过验证性因素分析确定了18个观察变量。使用结构方程模型分析方法，构建了提高数学建模满意度的路径模型，为我国高等学校数学建模教学提供了理论依据。

世界大学城；数学建模；翻转教学；结构方程模型

一、引言

翻转教学也称作翻转课堂(Flipped Classroom，Reverse Instruction， Inverse Teaching，等)、视频点播教学(Vodcasting Education)、 教育视频点播教学(Educational Video-on-Demand )等，也有翻译为反转教学或颠倒教学。翻转教学是将所谓传统教学的“课中环节和课后环节”颠倒为“课前环节和课中环节”所形成的一种教学模式。如果把“教师的教”理解为知识传授，“学生的学”理解为知识内化，那么翻转教学引起的这种流程变革所带来的则是知识传授的提前和知识内化的优化，这就是翻转教学的基本要义所在。经过教学流程的颠倒，促使了教与学本身的关系发生了变化，教与学的方式也发生了变化，这就是翻转教学彰显出来的逻辑魅力[1]。

全国大学生数学建模竞赛是由教育部高教司主办的，目前已成为全国高校规模最大的基础性学科竞赛，也是世界上规模最大的数学建模竞赛[2]。为了组织学生比赛，各个学校在“数学建模”和“数学实验”课程教学完成后还组织赛前强化培训等。然而，根据笔者长期(至少10年)以来的教学实践观察，在数学建模课程的教学中，存在着一个突出问题就是学生的学习效果不佳，教学满意度较低。经过反思，原因可能出在教学方式上。目前数学建模课程中比较普遍的教法是讲授法。选择讲授法的原因是，其一，每一次课都可以按照教学设计(教案)顺利完成教学任务。其二，每一学期也都可以按照授课计划顺利完成教学任务。其三，在学期当中的各类教学检查中可以顺利过关，不会出现麻烦甚至因为教学事故而被追责。可见，讲授法是从教师利益考虑的、最安全、最经济的一种教学方法，而从学生学习效果来看并不是较好的方法。

本研究以世界大学城为在线教学平台，设计了相应的翻转教学模式，连续实施了5个学期的数学建模教学，以满意度评估中影响力较大的美国顾客满意度指数模型(American Customer Satisfaction Index，简称ACSI)和技术接受模型(Technology Acceptance Model，简称TAM)为理论基础，编制了调查问卷，使用结构方程模型分析方法，构建了提高数学建模教学满意度的路径模型，为高等学校开展数学建模教学提供了数据支持和理论借鉴。

二、基于世界大学城环境下的数学建模翻转教学模式

世界大学城(worlduc)的宗旨是为每个机构建立一个资源共建共享型交互式教育学习网络服务平台，综合了远程教学、网络办公、即时通讯、商务管理、全民媒体、个性化数字图书馆等功能的一座既虚拟又真实的大学社区平台，为每个大学城居民建立了一个功能强大的终身学习空间[3]。建设世界大学城是教育信息化的一个重要举措。浙江工贸职业技术学院(下称“我院”)于2011年引进了世界大学城项目，是在全国范围内率先引进的高等院校之一。所有教职员工和所有学生都开通了自己的空间，而且通过积极建设使得个人空间达到了一定的水平，取得了一定的教学效果。

我国高等院校学生思想成熟、自学能力强、一般都具有电脑设备，这些都能很好地契合翻转课堂教学模式所要求的学生的学习特点，在教学中应用翻转教学模式具有很好的可行性[4]。因此我们设计了基于世界大学城环境下的数学建模翻转教学模式，其流程见图1所示。

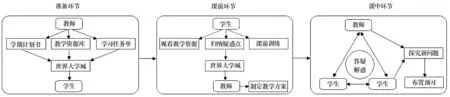
图1 数学建模翻转教学模式

从图1可见，数学建模翻转教学模式由准备环节、课前环节和课中环节构成。在准备环节，教师制订好学期授课计划，建设好(本节课)教学资源库，安排好(本节课)学习任务单，并把这些上传到世界大学城的教师空间里。学生准备好电脑，保证网络畅通，并在大学城注册成为居民。

在课前环节，学生通过登录世界大学城的教师空间，查阅(本节课)学习任务单，根据学习任务单，或者在线观看教学视频，或者下载电子文本(包括Word，PPT等)阅读，或者运行Matlab程序、Lingo程序反复实验，观察分析实验结果。该期间可以做笔记，可以完成课前训练题，归纳整理若干疑惑点，并在大学城教师空间留言。教师观看学生留言后制定本节课教学设计方案(教案)。

在课中环节，通过师生讨论、生生讨论弄懂疑惑点，掌握全部知识。教师鼓励学生自带电脑等设备到课堂，根据自己的学习步调进行个性化学习。如果课堂有剩余时间，还可以提出更深层次的问题供学生探究。在下课前，教师提醒或强调下节课的预习内容。

三、研究方法

本研究采用连续性的普查方法进行调查，即在数学建模选修课班级里，连续实施5个学期的翻转教学模式进行教学实验，每学期有学生50人，且每学期的学生是不同的，故样本总容量为250。本调查采用自制问卷来搜集数据，运用结构方程模型方法进行统计分析，并采用AMOS软件进行计算。

(一)调查问卷设计

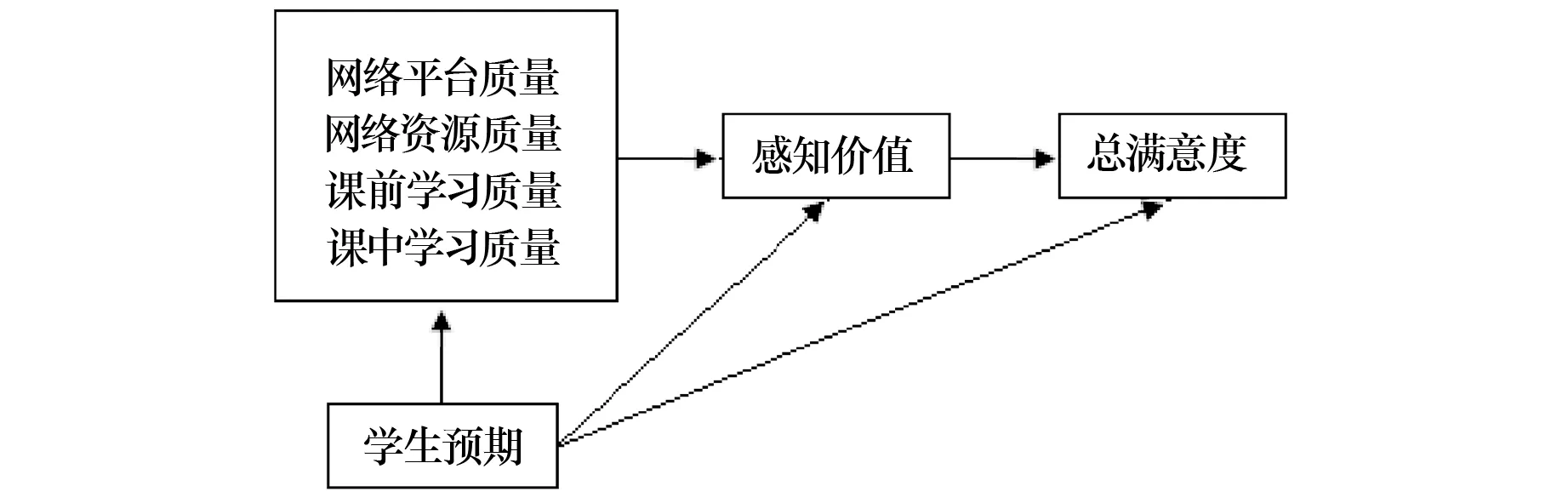
有研究将ACSI模型和TAM模型相结合，建立了我国翻转课堂学生满意度假设模型，见图2所示。

图2 翻转课堂学生满意度假设模型[5]

在图2模型中，“感知质量”包括3个维度，即网络平台维度、网络课堂维度和面授课堂维度。“感知质量”中没有反映出网络教学资源的质量，或者说将网络教学资源融入交互平台和网络课堂之中而没有单独体现出来。由于数学建模涉及的学习内容非常广泛，而本科生与专科生的学习内容又有着显著不同，对于本科生来说，如果没有高质量的教学案例，很难实现好的教学效果；对于专科生来说，如果缺乏“必需够用”的教学模块，那么整个学期的教学质量乃至于整个学年的竞赛成绩将大打折扣，因此我们将“网络教学资源”单独列为“感知质量”的一个维度。

本研究调查指标体系由4个一级指标构成，分别为感知质量、学生预期、感知价值和总满意度。其中“感知质量”又由4个二级指标构成，分别为网络平台质量、网络资源质量、课前学习质量和课中学习质量。调查问卷由21个题项构成，各题内容和结构见表1和表2所示。问卷选项采用LIKERT五级量表进行测试，从1～ 5 分别表示 “很不同意”“不同意”“一般”“同意”“很同意”。

鉴于个别学生缺席，发放问卷236份，回收236份，经过整理，剔除存在缺失项的4份，得到有效问卷232份，问卷有效率为98.3%。

(二)调查问卷检验

使用验证性因素分析法(简称CFA法)检验问卷的信度和效度(这里指结构效度)[6]212-243(见表1、表2)。

首先，针对“感知质量”进行验证性因素分析。各调查项目的因素负荷量见表1第3列，因素负荷量均处于0.5～0.95之间，表明测量模型(即指标结构)的基本适配度良好。各调查项目的信度系数见表1第4列，信度系数均超过了0.5，表明问卷的内在质量检验良好。各潜在变量的组合信度系数见表1第6列，组合信度系数均超过了0.6，表明问卷的内在质量理想。此外，各潜在变量的平均变异量抽取值见表1第7列，平均变异量抽取值均超过了0.5，也表明问卷的内在质量理想。

其次，针对总指标进行验证性因素分析。各调查项目的因素负荷量见表2第3列，因素负荷量均处于0.5～0.95之间，表明测量模型的基本适配度良好。各调查项目的信度系数见表2第4列，信度系数均超过了0.5，表明问卷的内在质量检验良好。各潜在变量的组合信度系数见表2第6列，组合信度系数均超过了0.6，表明问卷的内在质量理想。此外，各潜在变量的平均变异量抽取值见表2第7列，平均变异量抽取值均超过了0.5，也表明问卷的内在质量理想。

表1 “感知质量”指标结构与因素分析结果

表2 总指标结构与因素分析结果

注：Y1=X1+X2+X3；Y2=X4+X5；Y3=X6+X7+X8；Y4=X9+X10+X11

(三)结构方程模型分析方法

1.结构方程模型

结构方程模型(Structural Equation Modeling，简称SEM)是探索潜在变量之间因果关系的一种统计分析方法，通常包括测量模型和结构模型[6]1-71。

测量模型反映了潜在变量与其对应的观察变量之间的相互关系，测量模型的矩阵式方程为

其中，ξ为n×1矩阵，表示外因潜在变量；X为q×1矩阵，表示ξ的观察变量；δ为q×1矩阵，表示X的测量误差；ΛX为q×n矩阵，是X与ξ的关联系数矩阵。

η为m×1矩阵，表示内因潜在变量；Y为p×1矩阵，表示η的观察变量；ε为p×1矩阵，表示Y的测量误差；ΛY为p×m矩阵，是Y与η的关联系数矩阵。

结构模型反映了潜在变量之间的相互关系。潜在变量分为潜在原因变量和潜在结果变量。结构模型的矩阵式方程为

η=Bη+Γξ+ζ

其中，B为m×m矩阵，是潜在结果变量之间的关联系数矩阵；Γ为m×n矩阵，是潜在结果变量与潜在原因变量之间的关联系数矩阵；ζ为m×1矩阵，表示η的误差。

2.参数估计方法

使用最广泛的参数估计方法是极大似然估计法(简称ML法)，它适合于大样本且数据符合多变量正态性假定。如果数据为大样本但不符合多变量正态性假定，则采用一般最小平方法(简称GLS法)较好。

2.缺乏核心技术。核心技术是物联网产业发展的基础。目前来看，我国物联网核心技术大多为发达国家所掌握。如RFID关键技术、传感器技术、射频识别技术等。这些核心技术缺乏自主知识产权，容易被国外掐住脖子。同时，因技术原因，物联网技术过高的应用成本，使技术推广应用遇到极大阻碍。我国物联网企业亟待突破核心技术的瓶颈，否则，会严重阻碍我国物联网的顺利发展。

3.模型适配度检验方法

适配度是指假设的理论模型与实际数据的一致性程度。关于模型的适配度评价指标，需要同时考虑3个方面：基本适配度指标、整体模型适配度指标和模型内在结构适配度指标。整体模型适配度检验是关于模型外在质量的检验，模型内在结构适配度检验是对模型内在质量的检验，适配度大小代表了各测量模型的信度和效度。

基本适配度指标见表3，整体模型适配度指标见表4，模型内在结构适配度指标见表5。

表3 基本适配度检验项目与标准

表4 整体模型适配度检验的项目与标准

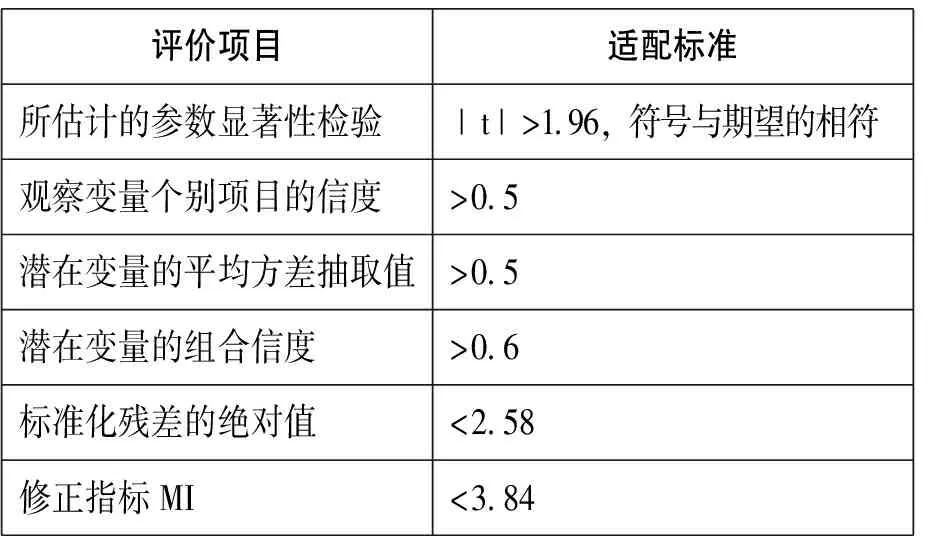
表5 模型内在适配度检验项目与标准

四、研究过程与结果

(一)结构方程模型的建立

根据图2的翻转课堂学生满意度假设模型，我们提出如下研究假设：(1)学生预期对感知质量、感知价值和总满意度均有正向影响。(2)感知质量对感知价值和总满意度均有正向影响。(3)感知价值对总满意度有正向影响。根据研究假设和表2中的指标体系，建立结构方程模型，如图3所示。

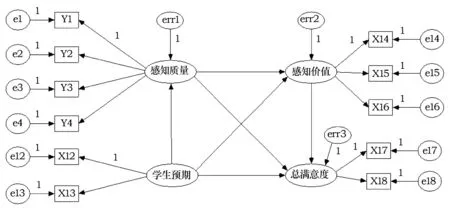
图3 数学建模翻转教学的结构方程模型

在图3中，“学生预期”是潜在原因变量，“感知质量”和“感知价值”是潜在中介变量，“总满意度”是潜在结果变量。

(二)模型界定搜寻

在图3中，路径“学生预期→感知质量”“学生预期→总满意度”“感知质量→感知价值”是必含的路径，其余路径交给AMOS自动搜寻。从搜寻结果中选择卡方值最小(或相伴概率最大)的3个模型，分别为模型1、模型2和模型3，它们所对应的路径如图4所示。

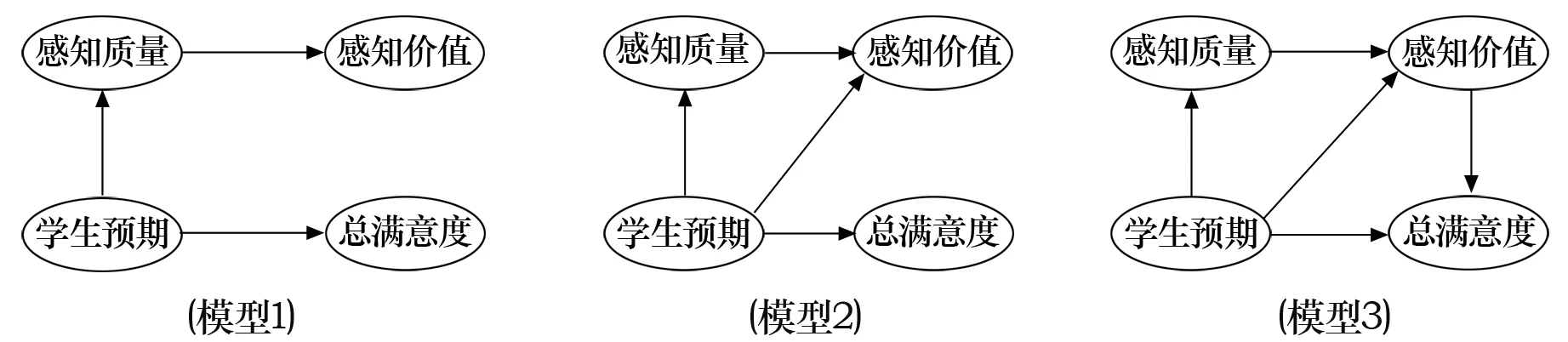
图4 模型界定搜寻结果

模型1、模型2和模型3的适配度检验结果如表6所示。

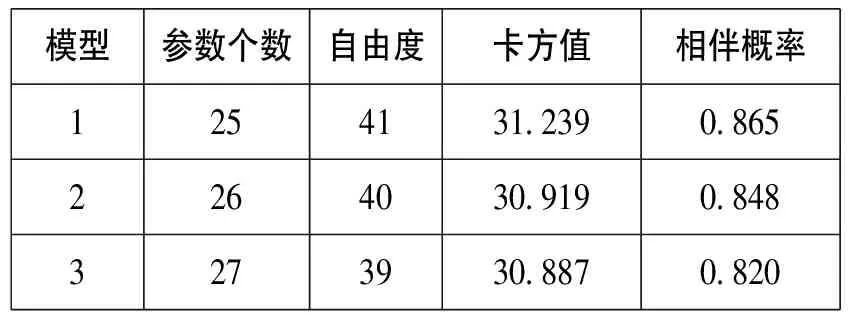
表6 模型界定搜寻的适配度检验结果

对于模型1和模型2，“总满意度”直接来自于“学生预期”，而“感知质量”和“感知价值”不直接影响“总满意度”，这显然不符合相关理论和研究假设，故舍去。

对于模型3，“感知质量”是通过“感知价值”影响“总满意度”的，而不是直接去影响“总满意度”，具有一定的合理性。

相比之下，模型3更符合相关理论，故将模型3作为最终的数学建模翻转教学结构方程模型。

(三)结构方程模型3的参数估计和检验

由于调查数据为大样本且不一定符合多变量正态性假定，故使用GLS法进行参数估计。非标准化估计值如图5所示。

图5 模型3的非标准化估计值

标准化估计值如图6所示。

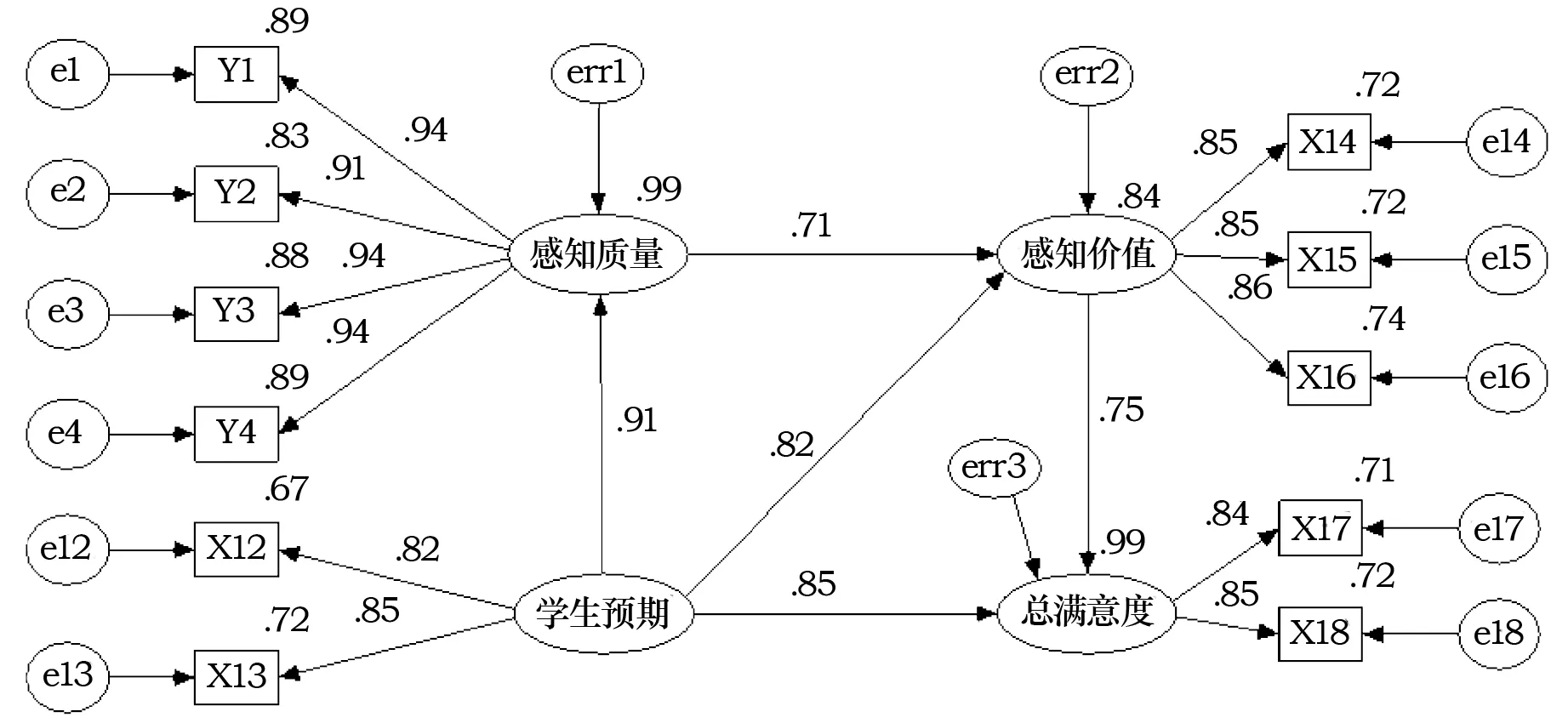
图6 模型3的标准化估计值

回归系数的显著性检验结果如表7所示。

表7 模型3的未标准化回归系数估计值

注：“*”表示相伴概率p<0.05，“**”表示p<0.01，“***”表示p<0.001。

从图5、图6和表1可知，所有误差变异量没有出现负值，所有因素的负荷量全部介于0.5～0.95之间，所有观察变量的测量误差均很小，表明模型基本适配度检验通过。

从表7可知，所估计的参数均达到显著水平，结合表2的信度检验结果可知，模型内在适配度检验通过。

整体模型适配度指标如表8所示。χ2值的显著性概率0.820>0.05，1

表8 整体模型适配度检验结果

(四)结果分析与讨论

1.测量模型的结果分析与讨论

(1)“网络平台质量”比“网络资源质量”更重要(权重系数0.94>0.91)，表明学生认为网络平台比网络资源更加重要。当代学生是互联网原居民，他们对互联网的依赖性很高。当学生利用互联网平台进行学习的时候，自然希望所依赖的互联网平台使用方便、功能全面、操作快捷，而对于网络资源来说，即使资源少一点也无大碍，毕竟还有纸质教材可以使用。(2)课前学习与课中学习同等重要(权重系数均为0.94)，表明学生充分认识到课前学习的重要性，充分认识到翻转学习再也不是过去那种可有可无的“预习”了。翻转学习突出课前学习的重要性，要求学生必须坚持课前观看网络资源，尽可能完成教师留下的学习任务，只有这样才能在课中展开讨论。如果学生课前不学习，那么将很难在课中消化接收所学知识。(3)“期望参加数学建模竞赛并得奖”比“满怀希望学好这门课程”更重要(权重系数0.85>0.82)。不论是数学建模选修课，还是数学建模竞赛培训课，大多数学生参加学习的直接目的就是参加竞赛，只有极少数学生是为了获得学分。学生这种明确的参赛目的来源于教师的宣传和学生的感染，因为在我校数学建模已经成为一个品牌，数学建模竞赛具有极大的吸引力。(4)对于数学建模课程的价值，学生认为获得“团队协作意识”比获得“知识”和“能力”更多更重要(权重系数0.86>0.85=0.85)。数学建模课程非常强调多人协作完成一项建模题目，而且很多题目仅凭一个人根本无法完成，这与高等数学或其他类似课程具有显著不同。在高等数学的学习中，很多情况下只需要一个人独立思考就可以了。(5)“相比其他教学方式，我更喜欢翻转教学”比“学完课程我非常满意”的贡献更大(权重系数0.85>0.84)。这说明在数学建模课程学习中学生的满意度更倾向于翻转学习，学生已经体会到翻转学习对于数学建模课程的重要性。

2.结构模型的结果分析与讨论

(1)在数学建模课程学习中，“学生预期”对于“感知质量”的促进作用大于其他两个潜在结果变量(权重系数0.91>0.82，0.91>0.85)，这说明学生在明确的参赛目的指导下积极利用网络平台和网络资源，通过课前学习和课中讨论，掌握数学建模课程知识，完成该课程的学习任务。(2)“感知质量”通过“感知价值”间接去影响“总满意度”，而不是直接影响“总满意度”，这一点与ACSI模型有所不同。可能的原因是：其一，虽然高质量的网络平台和网络资源会促进翻转学习效果，但学生或许并没有将这一功劳归功于翻转教学。相反，低质量的网络平台或网络资源会减弱翻转学习效果，而学生恰恰将这一不足迁怒于翻转教学，于是这一功一罪便将“感知质量”与“总满意度”的正向相关性变成不显著。其二，只有学生体会到了“感知价值”之后，即知道了数学建模的应用价值、提高了解决实际问题的能力、增强了团队协作意识之后，才能将“感知质量”转变为对翻转学习的“满意度”。

五、研究结论和建议

基于前面的结构方程模型，我们不但检验了借助世界大学城开展数学建模翻转教学模式的有效性，而且还获得了提高学生满意度的路径模型，如图7所示。

图7 提高学生满意度路径模型

学生预期是学习的起点，学生满意度(等价于教学质量)是教学的终极目标。为了提高教学质量，必须从以下几个方面着手：

首先，鼓励学生牢固树立高大上的学习目标，形成学习预期。在数学建模课程第一课里，教师要讲解数学建模课程的重要意义和应用价值，宣传全国大学生数学建模竞赛的悠久历史和国内国际赛况，展示我校开展数学建模活动取得的辉煌成果，从而激发学生学习数学建模课程的积极性，点燃他们心中的希望之火。

其次，鼓励学生养成课前上网学习的习惯，提高感知质量。千里之行始于足下，为了实现高大上的学习目标，就要从每一节课开始，把其中的知识点全部弄懂，遇到困难不退却，知难而进，持之以恒才能取得成功。

第三，鼓励学生开展团队协作学习，增强感知价值。在课程之初，就要求学生自愿组合，形成一个3人小组，不论是课前学习还是课中学习，均以3人小组为单位开展讨论。这样的3人小组还可以保持到校内竞赛和全国竞赛中去。

第四，鼓励学生积极参加各级各类数学建模竞赛，实现梦想，提高满意度和教学质量。参赛是数学建模不同于其他课程的一个显著标志，其既是学习数学建模课程的出发点，也是归宿，但不是唯一目的。学生在竞赛获奖，既能实现其个人的目标，也能实现集体目标，更能起到感染下届学生的作用。通过他们的现身说法和传帮带作用，使得数学建模协会的活动蓬勃开展起来，吸纳更多的学生参加到数学建模课程的学习中来，为下届数学建模奠定良好的基础。

[1]赵兴龙.翻转教学的先进性与局限性[J].中国教育学刊，2013(4)：65-68.

[2]全国大学生数学建模网站.庆祝全国大学生数学建模竞赛20周年(1992-2011)[EB/OL].(2011-10-03)[2016-02-01].http：//www.mcm.edu.cn/.

[3]百度百科.世界大学城[EB/OL].(2011-04-05)[2012-06-07].http：//baike.baidu.com/view/4990876. htm.

[4]卜彩丽，马颖莹.翻转课堂教学模式在我国高等院校应用的可行性分析[J].软件导刊，2013，12(7)：9-11.

[5]翟雪松，尹吉明，林莉兰.结构方程视角下我国翻转课堂满意度模型构建[J].高教探索，2015(5)：65-72.

[6]吴明隆.结构方程模型：AMOS的操作与应用[M].重庆：重庆大学出版社，2010.

(责任编辑 李世萍)

Research on the Path Analysis of Satisfaction Level ofMathematical Modeling Inversion Method Based on Structural Equation Model

YECong-xiang1，WANGJi-jian2

(1.School of Information and Communications，Zhejiang Industry & Trade Vocational College，Wenzhou，325027，China；(2.Faculty of Humanities，Zhejiang Industrial & Trade Vocational College，Wenzhou，325027，China)

In order to enhance the quality of mathematical modeling teaching method，the inversion teaching method based on the platform of World University City has been established and the elective mathematic modeling courses of five consecutive terms have been selected as teaching experimental classes.Combining with the domestic and foreign scales as well as questionnaires made by domestic universities，18 observed variables have been identified through the confirmatory factor analysis.Using the method of structural equation modeling, we constructs a path model to enhance the satisfaction level of mathematical modeling and provides theoretical basis for the universities'teaching of mathematical modeling in our country.

World University City；mathematical modeling；inversion teaching；structural equation model

2016-04-02

全国教育信息技术研究“十二五”规划2014年度专项课题“基于世界大学城环境下的数学建模翻转教学模式与应用效果研究”(项目编号：146231959).

叶聪相(1979-)男，浙江温州人，讲师，主要从事计算机多媒体技术应用教育研究.

G642

A