基于Matlab/Simulink的多路时空同步拦截弹阻尼环控制算法
王海枫,李豪杰
(南京理工大学 机械工程学院,南京 210094)
【装备理论与装备技术】
基于Matlab/Simulink的多路时空同步拦截弹阻尼环控制算法
王海枫,李豪杰
(南京理工大学 机械工程学院,南京 210094)
针对如何控制在多路时空同步拦截弹中不同时间发射的弹丸在同一时间飞行到目标点进行起爆这一问题,使用Matlab/Simulink仿真技术对弹丸的外弹道运动过程进行了建模,并基于这一模型分析了多路时空同步拦截弹的工作原理,进而设计了相应算法对弹载阻尼环的开环时间进行计算;以双路系统模型为例,对该算法以及其计算结果进行了仿真验证。结果表明:该算法具有较精确的修正能力,通过选择合适开环时间,拉长了先发射弹丸的飞行时间,实现了时空同步起爆;算法基于Matlab/Simulink仿真建模技术,整个计算过程清晰直观,提高了计算精度。
时空同步;Simulink;开环时间
在现代军事需求的牵引下,伴随着新技术的深入研究,各种信息化弹药应运而生。近年来,弹药数据链与可编程引信技术又为信息化弹药的实现提供了一种低成本的技术途径,在国内外得到了大力发展。因此,借鉴国外发展思路,为适应防空作战体系的建设要求,低成本信息化弹药的控制拦截武器系统将成为我国防空反导体系的一个重要组成部分。
在反导武器系统中,拦截弹主要担负末端防御任务,其使命任务为,近距离内拦截对方来袭的反舰导弹、反辐射导弹等小型高速目标,兼顾对海攻击。时空同步拦截弹基于一维修正弹技术。这种修正弹最先由美国提出,其目的就是将常规弹药智能化[1]。美国弹道修正弹3个研制阶段中的第2个阶段,主要是通过弹上引信装置实现纵向弹道的修正[2]。原理为,在弹丸实时飞行时测量出一段弹道参数,并与理想弹道参数进行比较,之后解算,形成控制指令,通过弹上引信控制阻尼环装置调节阻力,改变弹丸飞行速度,从而进行修正。这种技术是目前被广泛采用,成本较低的一种弹道修正技术[3-4]。
时空同步拦截弹在射击时采用顺序击发,相临两发弹间隔时间相同,通过可编程引信技术控制每发弹丸搭载的阻尼环在不同时间打开,进而改变弹丸飞行速度,控制不同时刻发射的多发弹在同一时刻到达同一目标点,起爆形成弹幕。因此在单发弹的飞行过程中,阻尼环打开时间的选择为控制弹丸在要求时间到达目标点的关键,也是整个拦截弹的关键。本文采用基于Matlab/Simulink建模的可视化技术对弹丸外弹道进行仿真[5]。并在仿真模型的基础上,设计了相应算法求取开环时间。
1 外弹道模型
1.1 运动模块
如图1所示,在二维坐标系下,弹丸在运动过程中主要受到重力和阻力作用,其中重力垂直于水平面向下,阻力始终与弹丸运动方向相反。其运动公式为
v·sinθ=w
v·cosθ=u
(1)
(2)
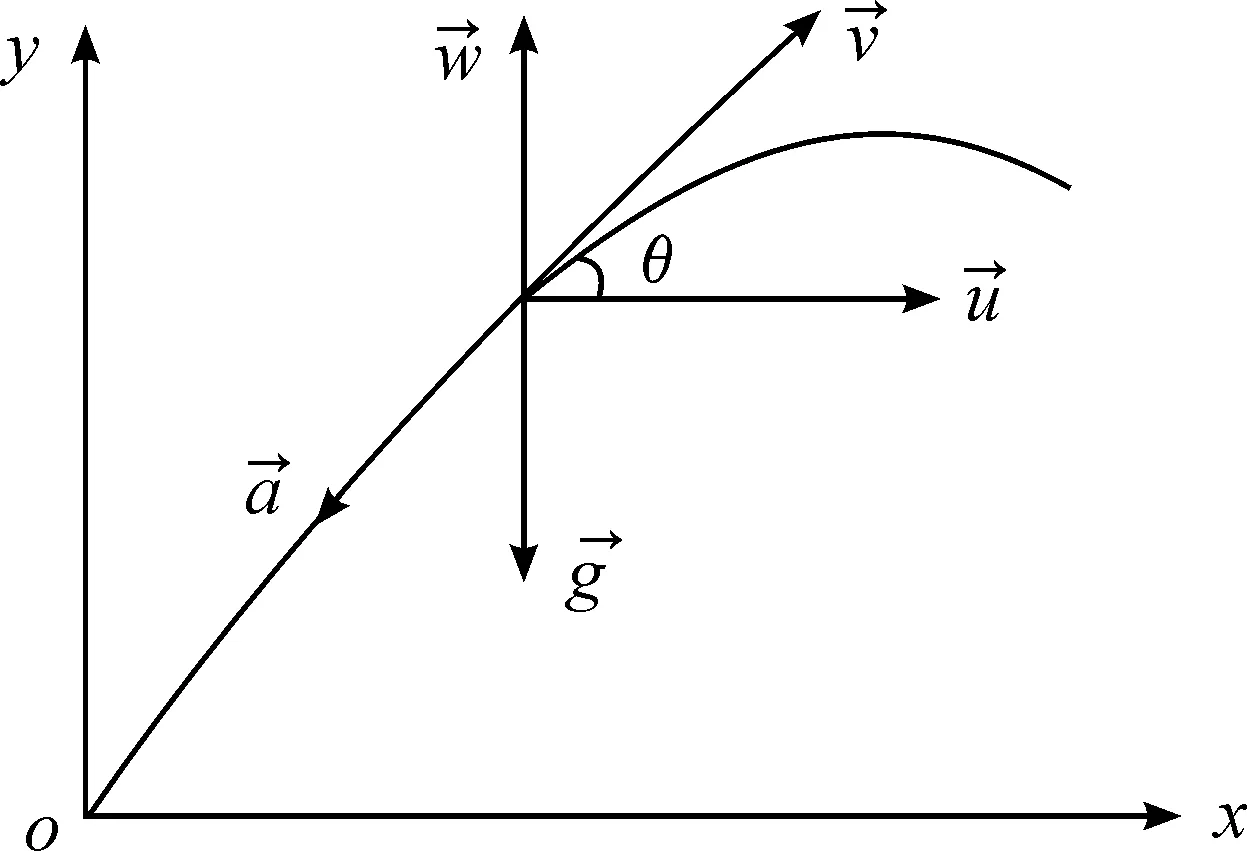
图1 二维坐标系下弹丸质心运动
1.2 阻力与气重函数模块
根据外弹道学理论[6-7],有
a=cH(y)F(v)=cH(y)vG(v)
(3)
将式(3)分别代入式(1),式(2)中,可得
其中H(y)是气重函数[8],表示了大气对弹丸运动的影响,其经验公式为
F(v)是空气阻力函数,表示弹丸相对于空气的运动速度对弹丸运动的影响。为了方便计算,F(vτ)也可由经验公式表示
当vτ<250时
当250≤vτ<400时
当400≤vτ≤1 400时
0.154 8vτ-26.63
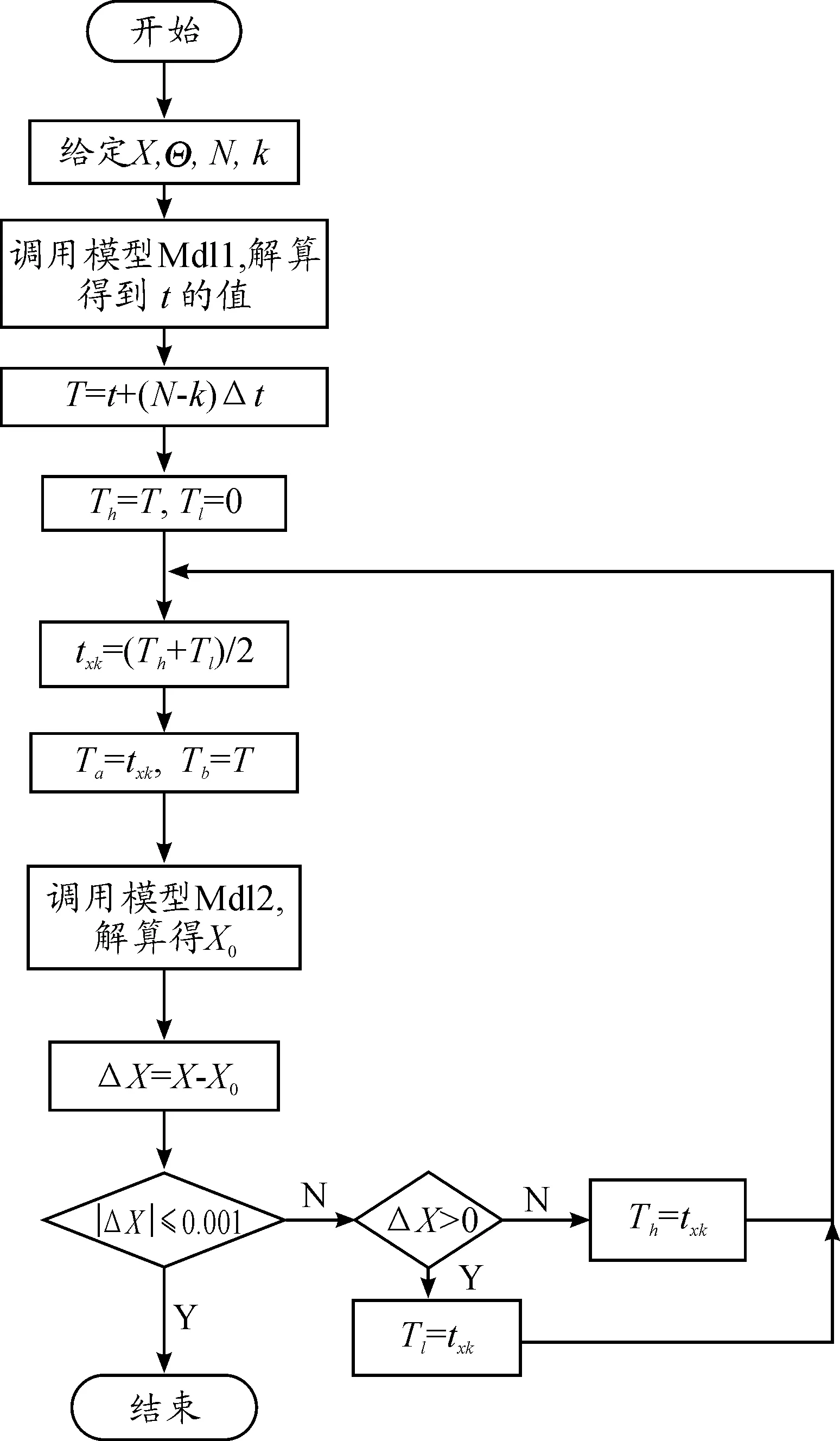
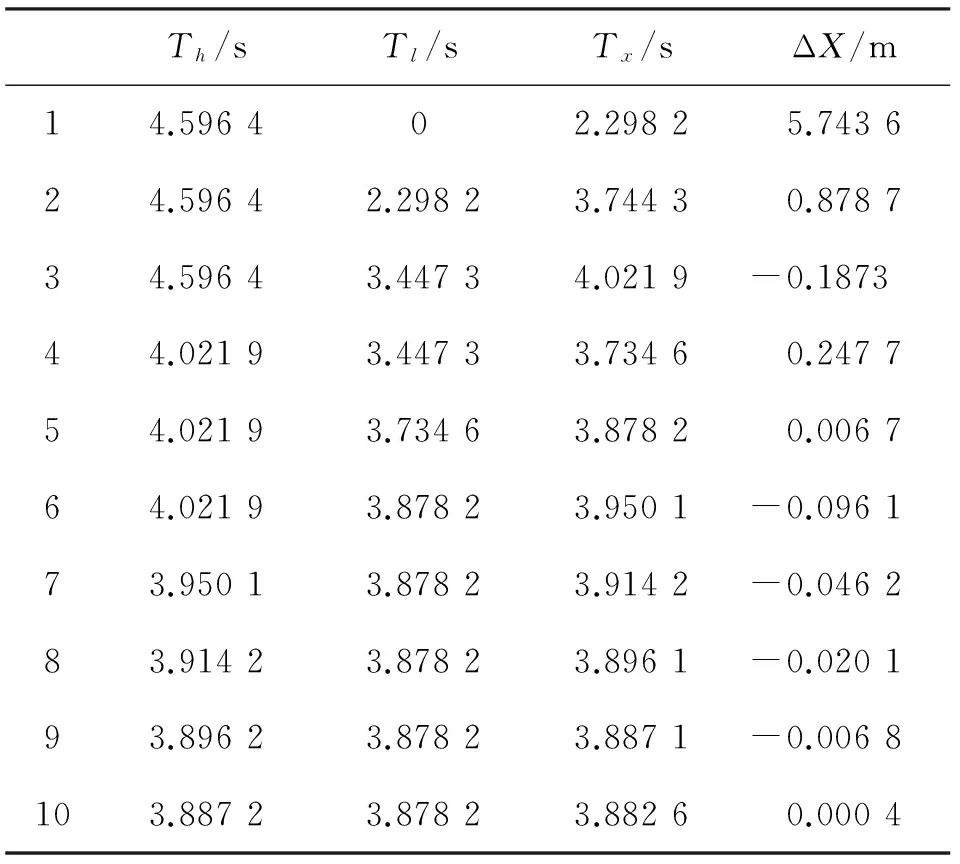
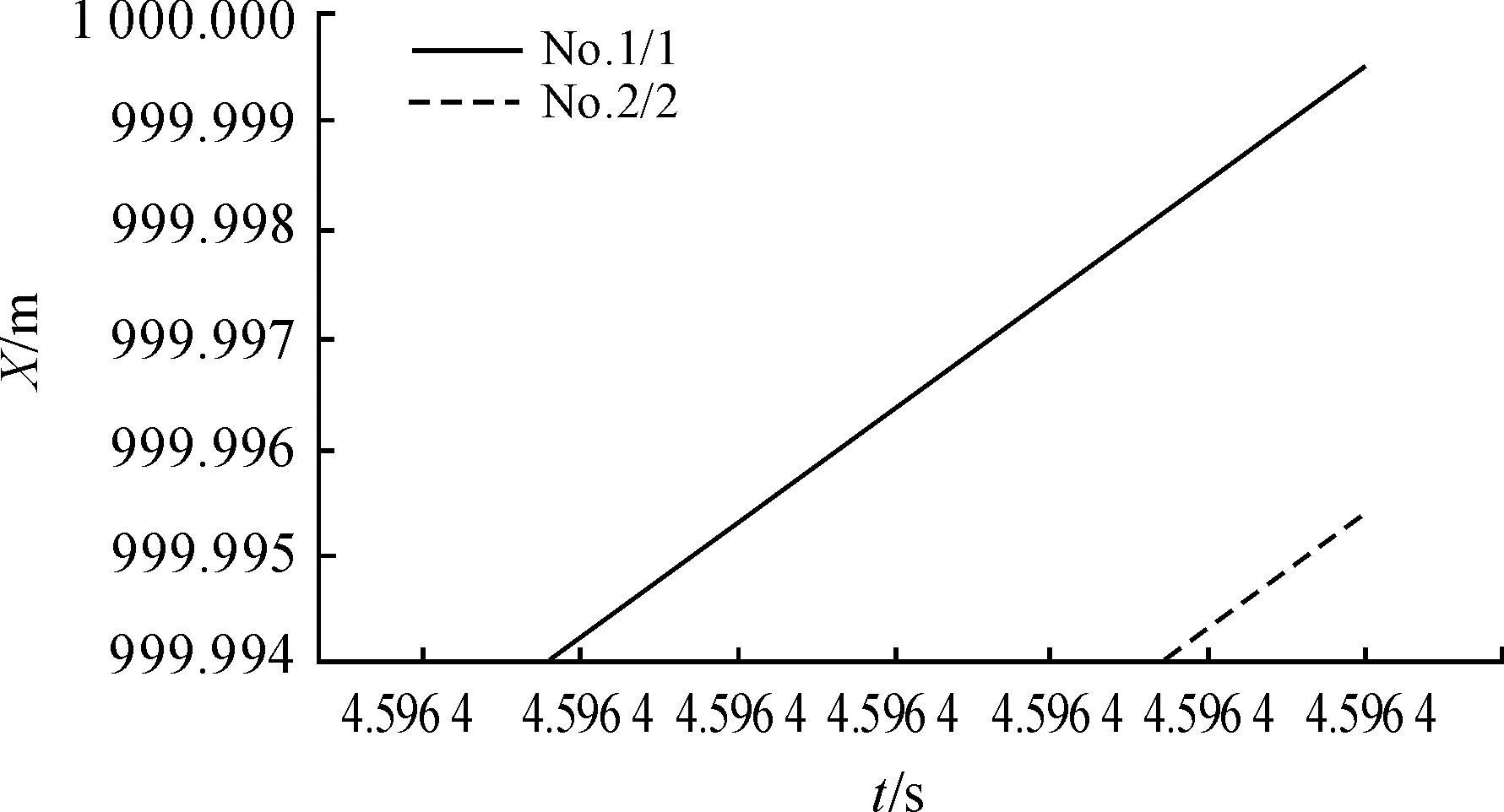
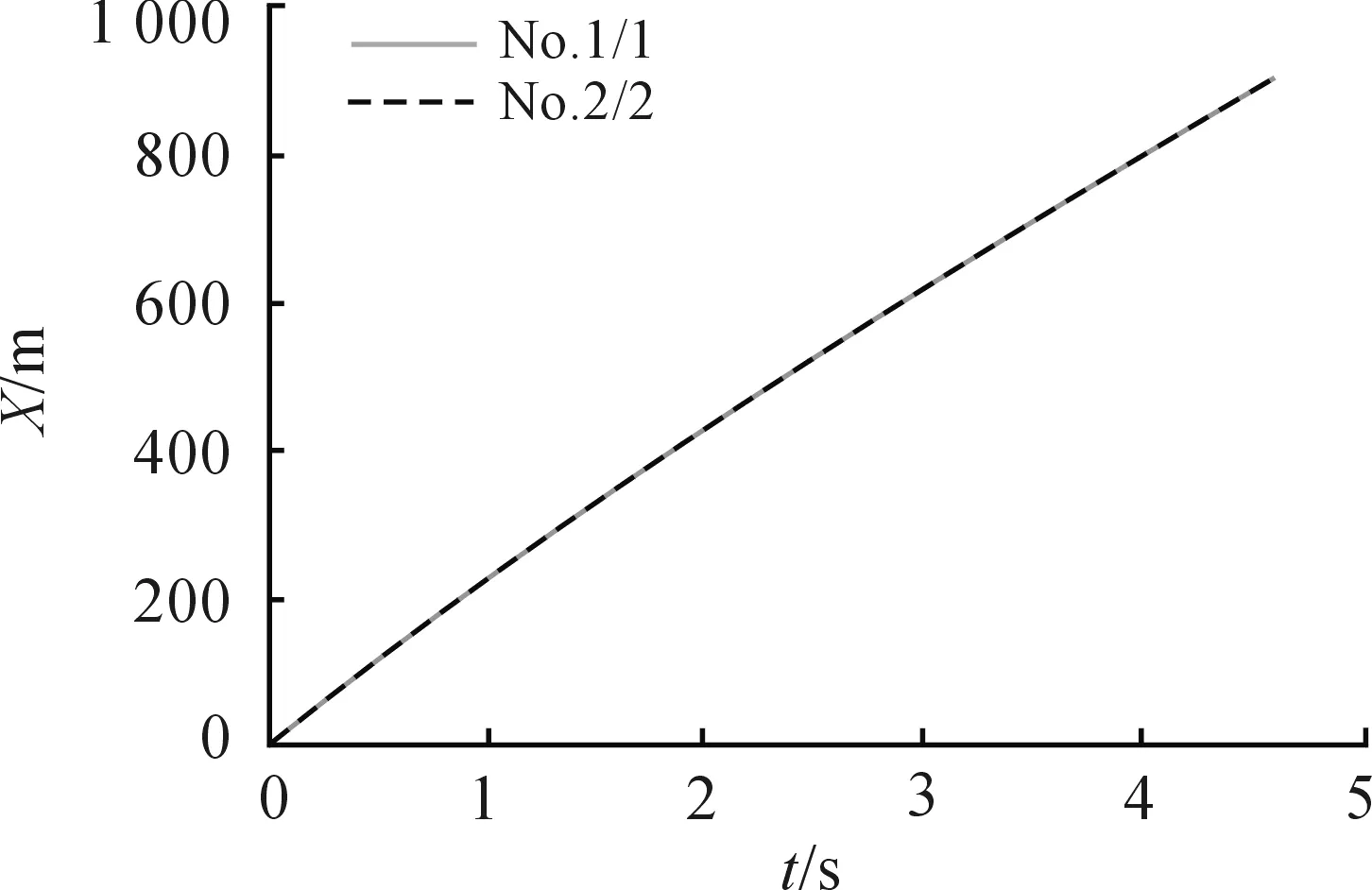
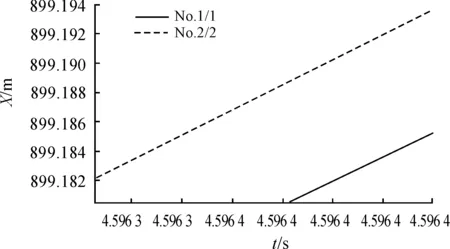
当1 400 本文主要研究弹丸发射初速在400 m/s以下的情况,所以使用前两种情况进行建模,模型如图2所示。 在经验公式中,vτ是弹丸在虚温下的速度,而τ和τon是一般状态下和标准状态下的虚温, 当弹丸飞行高度低于9 300 m 时,有 τ=τon-G1y 其中G1=6.328×10-3K/m,τon=288.9 K根据外弹道学理论,有 所以有 则虚温模块的模型如图3所示。 图3 虚温模块模型 1.3 阻尼环模块 c是弹丸运动的弹道系数,它反应了弹丸本身的组合特点。在一维修正弹的外弹道运行过程中,打开阻尼环本质上就是改变弹丸运动的弹道系数,使开环后的弹道系数大于开环前,从而降低弹丸运动速度,达到修正目的[9]。即当0≤t≤t0时,c=c0;当t0≤t时,c=c1。其Simulink模型如图4所示。 图4 阻尼环模块模型 在模型中,运用比较模块与时钟进行比较,在Ta时刻将弹道系数从C0变为C1。 1.4 单发一维修正弹仿真模型 根据上文建立的一维修正弹弹丸的外弹道运动的数学模型,确定各模块之间的输入输出关系,将独立的模块连接到一起,建立弹丸外弹道运动系统仿真模型如图5所示。其中除了用到连续积分模块外,还用到大量的数学模块,以及自定义函数等其他模块。在仿真结果上仍采用多种输出和显示的形式,用XYGraph模块显示弹丸运动轨迹曲线;用示波器Scope模块显示横向和纵向的飞行距离变化以及弹道倾角和速度随时间变化的曲线[10-11]。 图5 一维弹道修正弹外弹道仿真模型 由于整个模型过于复杂,可以使用Simulink提供的子系统封装技术,将整个模型封装成一个模块,如图6所示。 图6 仿真子系统模型 其中,v_in是发射初速,θ_in是射角,Ta是阻尼环打开的时间,Tb是弹丸起爆时间。 根据弹丸的初始速度、初始射角以及弹道系数等设定各个仿真模块参数。在仿真时,采用变步长连续算法,选用基于精确龙格—库塔(4,5)的Dormand-Prince算法,它是一步算法,在计算时只需要知道前一刻的值。最大和最小步长设置为自动调节,由于拦截弹对精度要求较高,所以相对误差允许范围为10-4,绝对误差允许范围设置为自动调节[12-13],通过比较模块比较时钟信号与Tb输入,当计时达到Tb时,仿真自动结束。 1.5 多路一维修正弹弹道模型 对多发弹丸系统的建模基于单发弹弹道模型的基础,将多个封装好的子系统模型集成在一起。运用使能子系统模块,在特定条件下,运行子系统模型,模拟弹丸的飞行过程。以双路弹道为例,其模型如图7所示。 图中T1,T2为弹丸发射时间,所以可以通过对发射时间的选择,实现两发弹丸的顺序击发。 图7 双路弹道系统模型 2.1 算法原理 在时空同步拦截弹中,需要控制阻尼环的打开时间,控制等间隔时间发射的弹丸同时达到同一地点起爆,形成有效弹幕对导弹进行拦截。 一般拦截弹目标限定为水平射程为2 000 m以内的空中目标,由于射程近,飞行时间短,所以弹丸运动过程没有下落过程,水平方向射程与竖直方向的射高均随着时间增大,并且时间曲线均近似于线性上升。由上所述,打开阻尼环导致的弹丸减速并不会明显改变弹道轨迹,其主要目的在于拉长先发弹丸到达目标点的时间。所以开环时间的选取对于射程与时间的函数和射高与时间的函数来说,所带来的影响近似相同。而由于多路拦截弹需要在空中形成有效弹幕,则在水平射程需要更高的精度,所以使用弹丸运动的水平距离与时间的函数关系为基础设计算法对开环时间进行求取。 设拦截弹共有N发弹丸,Δt为发射时间间隔。以最后发射的第N发弹为基准,假设该弹丸到达水平射程为X的目标点O的用时为tN,则与此弹丸相邻发射的第N-1发弹到达目标点O的时间应为tN+Δt,第N-2发弹到达目标点O的时间为tN+2Δt。则第k发弹到达目标点O的时间为tN+(N-k)Δt。 设弹丸未打开阻尼环时的速度函数为v1(t),打开阻尼环后的速度函数为v2(t),则第N发弹到达目标点O的运动过程为 第k发弹到达目标点O的运动过程为 其中txk为阻尼环的开环时间,以此类推,第一发弹到达目标点O的运动过程为 2.2 算法实现过程 在时空同步拦截弹中,首先需要根据弹丸的运动公式以及目标射程,求出不需要打开阻尼环的第N发弹到达目标点的时间,再根据该时间求取出各发弹的飞行时间,进而利用算法求出每发弹丸的开环时间。 为达到这一目的,设计了基于Simulink仿真模型的算法,用以计算弹丸运动中的开环时间。 首先根据目标方位给定弹丸的射程X和发生角度θ,然后根据弹丸不开环情况下的运动模型mdl1(图8)解算出第N发弹丸到达目标点的运动时间t,再进一步求得其他弹丸到达目标点的运动时间。 图8 弹丸不开环运动模型 假设弹间发射间隔时间为为Δt,则第k弹与第N发弹的发射间隔时间为(N-k)Δt,所以第k发弹运动时间应为 T=t+(N-k)Δt 算法的目的为如何在[0,T]的时间区间内,找到某一时刻txk打开阻尼环,改变弹丸运动的弹道系数,进而改变弹丸的运动轨迹,使弹丸在T时刻到达射程为X的目标点,完成起爆。 设有Th,Tl,令Th=T,Tl=0,则有 txk=(Th+Tl)/2 将txk代入到如图5所示的mdl2模型中,令Ta=txk,Tb=T,进行仿真求解得弹丸的飞行距离X0。计算目标射程与仿真所得的实际射程的差值为 ΔX=X-X0 当|ΔX|≤0.001时,可以认为仿真所得的实际射程与目标射程相等,仿真结束,此时所求得txk即为该发弹丸应该打开阻尼环的时间;当|ΔX| >0.001时,继续判断ΔX是否大于0,当ΔX>0时,说明实际射程没有达到目标射程,阻尼环打开时间过早,需要在[txk,Th]时间区间内继续仿真,即令Tl=txk,重复上述步骤,直至仿真结束;当ΔX<0时,说明实际射程已经超出了目标射程,阻尼环打开时间过迟,需要在[Tl,txk]时间区间内继续仿真,即令Th=txk,重复上述步骤,直至仿真结束。算法流程图如图9所示。 图9 算法流程 以射速323 m/s,发射角度π/4,目标射程1 000 m为初始条件进行仿真,调用mdl1,计算得t=4.593 9 s,如图10所示。 以最后两发弹为例,令Δt=0.002 5 s,则T=4.596 4 s,仿真数据如表1所示。 在第10次循环后,仿真所得ΔX的绝对值小于1 mm,达到要求精度,仿真结束。此时求得tx=3.882 6 s。 调用图7所示的双路弹道模型,设T1=0,T2=0.002 5 s。第一路的Ta=3.882 6 s;第二路模拟不开环的情况,所以Ta>Tb即可,令这一路Ta=10 s,射角θ=π/4,Tb=4.596 4 s。仿真参数设置与前文一致,开始进行仿真。 图10 mdl1计算结果 表1 算法循环内计算数据 图11为双路弹道水平射程X与时间t的关系曲线,曲线显示水平射程X随时间t而近似线性增大,并且由于时间间隔Δt为ms级,两弹道之间的相隔很近,接近重合。所以分时发射,同时到达目标点的特点很难观察,将图像中原点以及t=4.596 4 s处放大,如图12,图13所示。 图11 双路弹道射程与时间关系 在图12中可以看出,1号曲线由原点开始,水平射程X随时间t增大,表示在t=0时第一路弹丸发射;2号曲线在t=0.002 5处开始,水平射程X随时间t增大,表示第二路弹丸在t=0.002 5 s时发射。两条曲线平行上升,这是因为在弹丸运动初期,第一路弹丸尚未打开弹载阻尼环,此时两路弹丸弹道相同,所以两条曲线平行上升。 图12 双路弹道射程与时间关系原点处放大图 而从图13中可以看出,在t=4.596 4 s时1号曲线的水平射程为999.999 5 m,与表1数据一致,误差精度在算法要求的1 mm以内。由于在计算最终的起爆时间Tb时,将0.1 ms以下的时间全部舍去,所以仿真所得的2号曲线最终的达到的水平射程999.995 5 m要略低于目标射程1 000 m,误差也在mm级。而且图中1号曲线的斜率要略低于2号曲线,说明弹丸在飞行途中打开了阻尼环来降低飞行速度。 图13 双路弹道射程与时间关系4.596 4 s处放大图 图14是弹丸运动过程中竖直方向射高随时间变化的曲线。图15则是图14在t=4.596 4 s处放大的曲线。 从图15可以看出,当t=4.596 4 s时,1号曲线的竖直方向射高为899.193 8 m,2号曲线的竖直方向射高为899.185 2 m。两发弹竖直方向间距为0.008 6 m。说明阻尼环的张开对弹丸运动过程中射高的影响比射程略大,但其散布精度仍保持在mm级。 综合图13与图15,可以得出在二维平面内,间隔0.002 5 s发射的两发弹丸在同一时间运动到同一目标的落点。在理想情况下,仿真计算得到的两发弹的落点误差在1 mm以内。 图14 双路弹道射高与时间关系 图15 双路弹道射高与时间关系4.596 4 s处放大图 本文使用Matlab/Simulink对基于一维弹道修正弹的时空同步拦截弹进行了弹道建模,通过所建模型对其工作原理进行了分析。从而设计了基于弹丸水平射程与时间的函数的二分法算法求取弹载阻尼环的打开时间。与传统算法相比,基于Matlab/Simulink模型的算法具有简单、清晰、计算精度高的特点,并且在运算以及理解过程中更加直观。最后通过双路弹丸系统的运动模型模拟双发拦截弹的运动情况,对算法进行仿真验证。仿真结果表明在理想情况下,该算法计算得出的开环时间可以控制间隔发射的两发弹丸在同一时间的落点精度到达mm级,提高了计算精度,对后续更加精确的弹道诸元的计算以及在实际情况下的各种误差分析提供了参考。 [1] GAO M.Actual Trajectory Detection for Trajectory Correction Projectiles[J].Journal of Ballistics.2003,15(1):87-92. [2] 邱荣剑,陶杰武,工明亮.弹道修正弹综述[J].国防技术基础,2009(8):45-4. [3] 王中原,史金光,李铁鹏.弹道修正中的控制算法[J].弹道学报,2011,23(2):19-21. [4] PETTERSSON T,BURETTA,COOK D.Aerodynamics and Flight Stability for A Course Corrected Artillery Round[C]//Proceedings of the 23rd International Symposium on Ballistics.Madrid,Spain:Graficas Couche,2007:647-654. [5] 陈桂明.应用MATLAB建模与仿真[M ].北京:科学出版社,2001. [6] 浦发,芮筱亭.外弹道学[M].北京:国防工业出版社,1989. [7] 郭锡福,赵子华.火控弹道模型理论及应用[M ].北京:国防工业出版社,1997. [8] 刘俊邦,张猛,朱建锋.非标准气象条件下火炮外弹道仿真[J].指挥控制与仿真,2013,35(2): 80-84. [9] 王宝全,李世义,申强,郭泽荣.一维弹道修正引信阻尼弹道系数的优化与仿真[J].弹道学报, 2002,14(4):67-73. [10]辛长范.基于Simulink的质点外弹道模型仿真[J].火力与指挥控制,2004,29(6):29-40,44. [11]张维.基于MATLAB的武器外弹道仿真可视化技术研究[D].中北大学,2014. [12]王江,付文利.基于MATLAB/Simulink系统仿真权威指南[M].北京:机械工业出版社, 2013. [13]CHAPMAN S J.MATLAB Programming for Engineers[M].CA:Brooks,2002. [14]张丽艳, 杜忠华,张志安,等.一维弹道修正弹分段解算控制算法的研究[J].火力与指挥控制,2015(8):143-145. (责任编辑周江川) Damping Ring Control Algorithm of the Mutiplex Time-Space Synchronization Interception Missile Based on Matlab/Simulink WANG Hai-feng,LI Hao-jie (School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China) To solve the problem of controlling the mutiplex time-space synchronization interception missiles which are launched at different time to reach the target at the same time and then to detonate, the model of the exterior trajectory moving process was established by Matlab/Simulink simulation technology. Basing on this model, the principle of the mutiplex time-space synchronization interception missiles was analyzed. And a corresponding algorithm for calculating the open-loop time of missile-borne damping ring was designed. At last, using the two-path model to simulate and verify the open-loop time which is chose-by the algorithm. The results show that the algorithm has accurate correction feasibility. By selecting suitable open-loop time, the two-path model prolongs the flight time of the first missile and then realizes time-space synchronization detonation. The algorithm based on Matlab/Simulink simulation and modeling technologies improves the calculation accuracy and the whole calculation process is clear and visual. time-space synchronization; Simulink; open-loop time 2016-07-09; 国家自然科学基金资助项目(61403201);中央校基本科研业务费专项基金资助项目(30915118824) 王海枫(1991—),男,硕士研究生,主要从事智能化弹药研究。 10.11809/scbgxb2016.12.017 王海枫,李豪杰.基于Matlab/Simulink的多路时空同步拦截弹阻尼环控制算法[J].兵器装备工程学报,2016(12):68-74. format:WANG Hai-feng,LI Hao-jie.Damping Ring Control Algorithm of the Mutiplex Time-Space Synchronization Interception Missile Based on Matlab/Simulink[J].Journal of Ordnance Equipment Engineering,2016(12):68-74. TJ012 A 2096-2304(2016)12-0068-07 修回日期:2016-08-15
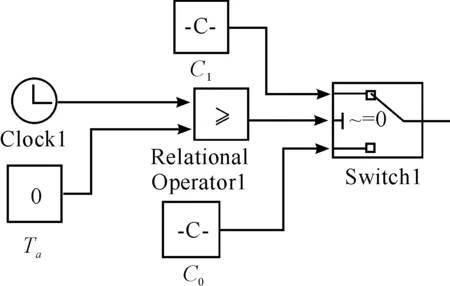
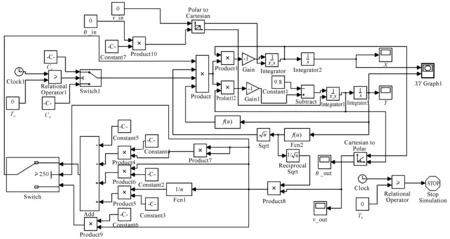


2 算法设计
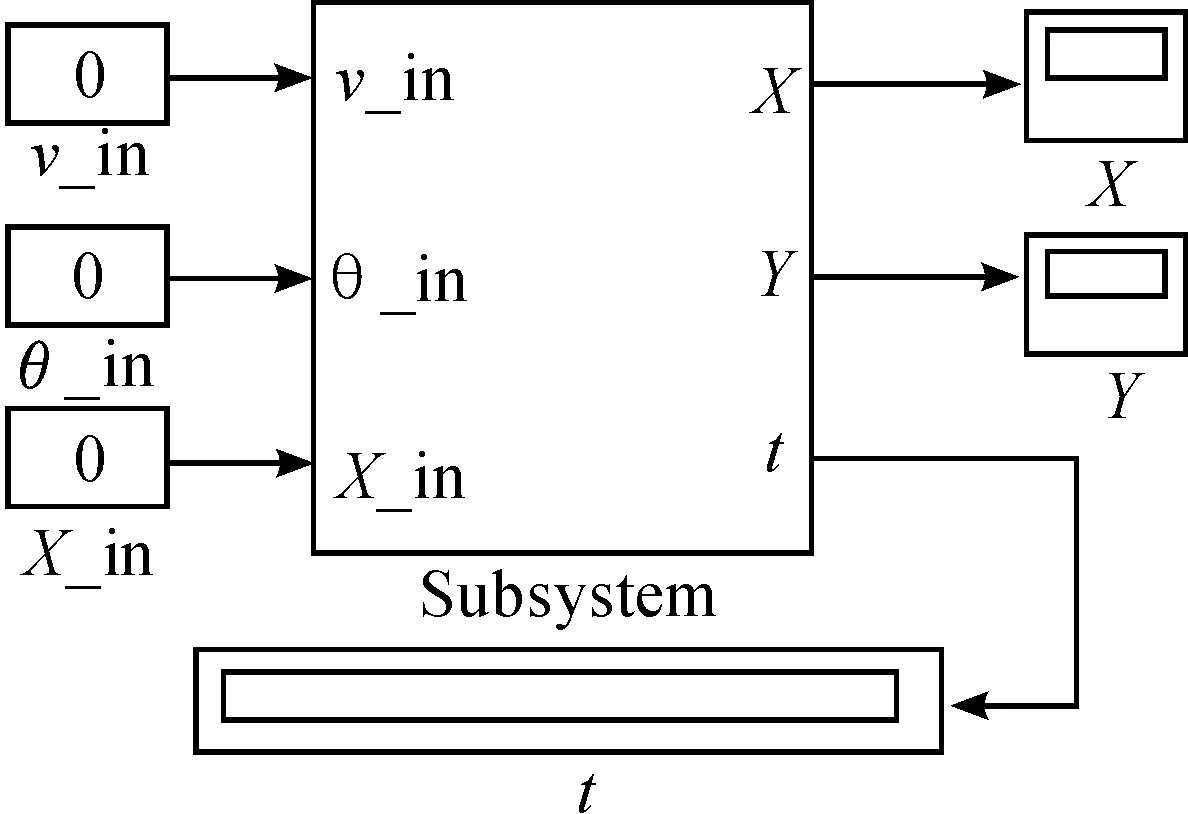
3 仿真实例



4 总结

